5.3.1 函数的单调性(教案)-高中数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 5.3.1 函数的单调性(教案)-高中数学人教A版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 898.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 10:39:42 | ||
图片预览

文档简介
第五章 一元函数的导数及其应用
5.3.1函数的单调性
教学设计
一、教学目标
1.结合实例,借助几何理解可导函数的单调性与其导数的关系.
2.能根据导数判断函数的单调性以及求解函数的单调区间.
3.能够利用函数的单调性解决有关问题.
4.体会导数法判断函数的单调性的优越性.
二、教学重难点
1、教学重点
根据导数判断函数的单调性以及求解函数的单调区间.
2、教学难点
利用函数的单调性解决有关问题.
三、教学过程
1、新课导入
在高一的学习中,我们研究了函数的单调性,最值等性质,在本章的学习中,我们学习了导数的概念及其运算,那么导数与函数的单调性之间有什么关系呢,能否用导数更加精准地研究函数的单调性呢,带着问题开始本节课的学习吧.
2、探索新知
一、函数的单调性与导数的关系
一般地,函数的单调性与导函数的正负之间具有如下的关系:
在某个区间上,如果,那么函数在区间上单调递增;
在某个区间上,如果,那么函数在区间上单调递减.
例1 利用导数判断下列函数的单调性:
(1);(2),;(3).
解:(1)因为,所以.
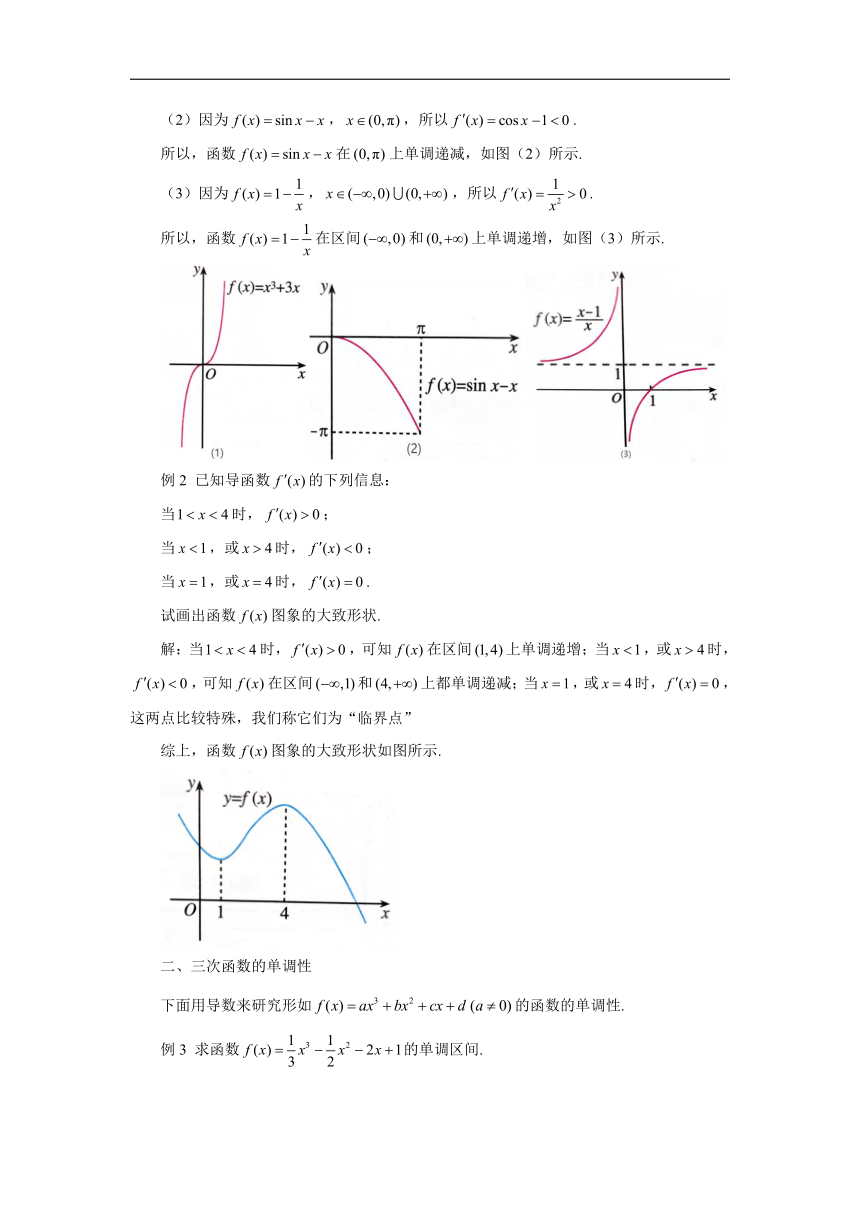
所以,函数在R上单调递增,如图(1)所示.
(2)因为,,所以.
所以,函数在上单调递减,如图(2)所示.
(3)因为,,所以.
所以,函数在区间和上单调递增,如图(3)所示.
例2 已知导函数的下列信息:
当时,;
当,或时,;
当,或时,.
试画出函数图象的大致形状.
解:当时,,可知在区间上单调递增;当,或时,,可知在区间和上都单调递减;当,或时,,这两点比较特殊,我们称它们为“临界点”
综上,函数图象的大致形状如图所示.
二、三次函数的单调性
下面用导数来研究形如的函数的单调性.
例3 求函数的单调区间.
解:函数的定义域为R.
对求导数,得.
令,解得或.
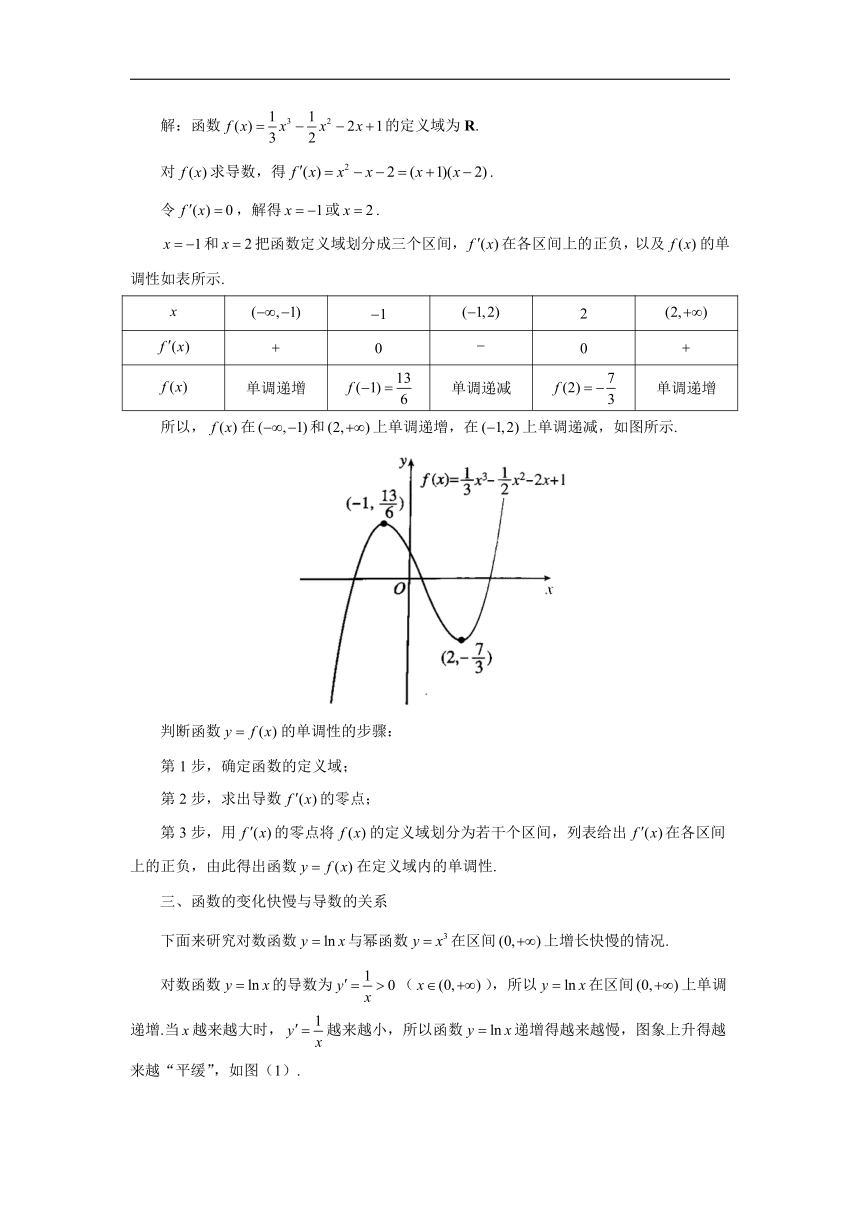
和把函数定义域划分成三个区间,在各区间上的正负,以及的单调性如表所示.
2
0 0
单调递增 单调递减 单调递增
所以,在和上单调递增,在上单调递减,如图所示.
判断函数的单调性的步骤:
第1步,确定函数的定义域;
第2步,求出导数的零点;
第3步,用的零点将的定义域划分为若干个区间,列表给出在各区间上的正负,由此得出函数在定义域内的单调性.
三、函数的变化快慢与导数的关系
下面来研究对数函数与幂函数在区间上增长快慢的情况.
对数函数的导数为(),所以在区间上单调递增.当越来越大时,越来越小,所以函数递增得越来越慢,图象上升得越来越“平缓”,如图(1).
幂函数的导数为(),所以在区间上单调递增. 当越来越大时,越来越大,函数递增得越来越快,图象上升得越来越“陡峭”,如图(2).
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.
例4 设,,,两个函数的图象如图所示.判断,的图象与,之间的对应关系.
解:因为,,所以,.
当时,;
当时,;
当时,.
所以,,在上都是增函数.在区间上,的图象比的图象要“陡峭”;在区间上,的图象比的图象要“平缓”.
所以,,的图象依次是图中的,.
3、课堂练习
1.函数的单调增区间是( )
A., B.
C. D.
答案:A
解析:因为,所以.令,得或,所以函数的单调增区间为,.
2.函数在上的单调性是( )
A.单调递增
B.单调递减
C.在上单调递减,在上单调递增
D.在上单调递增,在上单调递减
答案:C
解析:由已知得函数的定义域为,,令,得;令,得,函数在上单调递减,在上单调递增.
3.已知定义在上的函数的导函数,且,则实数m的取值范围为__________.
答案:
解析:因为,所以函数在上单调递增,所以,解得.
4.若函数在区间上具有单调性,则a的取值范围是______
答案:
解析:,函数在区间上具有单调性等价于或在上恒成立,则或,即或.
4、小结作业
小结:本节课学习了函数的单调性与导数的关系,判断函数单调性的步骤以及函数的变化快慢与导数的关系.
作业:完成本节课课后习题.
四、板书设计
5.3.1 函数的单调性
1.函数的单调性与导数的关系:一般地,函数的单调性与导函数的正负之间具有如下的关系:在某个区间上,如果,那么函数在区间上单调递增;在某个区间上,如果,那么函数在区间上单调递减.
2.判断函数的单调性的步骤:
第1步,确定函数的定义域;
第2步,求出导数的零点;
第3步,用的零点将的定义域划分为若干个区间,列表给出在各区间上的正负,由此得出函数在定义域内的单调性.
3.函数的变化快慢与导数的关系:一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.
5.3.1函数的单调性
教学设计
一、教学目标
1.结合实例,借助几何理解可导函数的单调性与其导数的关系.
2.能根据导数判断函数的单调性以及求解函数的单调区间.
3.能够利用函数的单调性解决有关问题.
4.体会导数法判断函数的单调性的优越性.
二、教学重难点
1、教学重点
根据导数判断函数的单调性以及求解函数的单调区间.
2、教学难点
利用函数的单调性解决有关问题.
三、教学过程
1、新课导入
在高一的学习中,我们研究了函数的单调性,最值等性质,在本章的学习中,我们学习了导数的概念及其运算,那么导数与函数的单调性之间有什么关系呢,能否用导数更加精准地研究函数的单调性呢,带着问题开始本节课的学习吧.
2、探索新知
一、函数的单调性与导数的关系
一般地,函数的单调性与导函数的正负之间具有如下的关系:
在某个区间上,如果,那么函数在区间上单调递增;
在某个区间上,如果,那么函数在区间上单调递减.
例1 利用导数判断下列函数的单调性:
(1);(2),;(3).
解:(1)因为,所以.
所以,函数在R上单调递增,如图(1)所示.
(2)因为,,所以.
所以,函数在上单调递减,如图(2)所示.
(3)因为,,所以.
所以,函数在区间和上单调递增,如图(3)所示.
例2 已知导函数的下列信息:
当时,;
当,或时,;
当,或时,.
试画出函数图象的大致形状.
解:当时,,可知在区间上单调递增;当,或时,,可知在区间和上都单调递减;当,或时,,这两点比较特殊,我们称它们为“临界点”
综上,函数图象的大致形状如图所示.
二、三次函数的单调性
下面用导数来研究形如的函数的单调性.
例3 求函数的单调区间.
解:函数的定义域为R.
对求导数,得.
令,解得或.
和把函数定义域划分成三个区间,在各区间上的正负,以及的单调性如表所示.
2
0 0
单调递增 单调递减 单调递增
所以,在和上单调递增,在上单调递减,如图所示.
判断函数的单调性的步骤:
第1步,确定函数的定义域;
第2步,求出导数的零点;
第3步,用的零点将的定义域划分为若干个区间,列表给出在各区间上的正负,由此得出函数在定义域内的单调性.
三、函数的变化快慢与导数的关系
下面来研究对数函数与幂函数在区间上增长快慢的情况.
对数函数的导数为(),所以在区间上单调递增.当越来越大时,越来越小,所以函数递增得越来越慢,图象上升得越来越“平缓”,如图(1).
幂函数的导数为(),所以在区间上单调递增. 当越来越大时,越来越大,函数递增得越来越快,图象上升得越来越“陡峭”,如图(2).
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.
例4 设,,,两个函数的图象如图所示.判断,的图象与,之间的对应关系.
解:因为,,所以,.
当时,;
当时,;
当时,.
所以,,在上都是增函数.在区间上,的图象比的图象要“陡峭”;在区间上,的图象比的图象要“平缓”.
所以,,的图象依次是图中的,.
3、课堂练习
1.函数的单调增区间是( )
A., B.
C. D.
答案:A
解析:因为,所以.令,得或,所以函数的单调增区间为,.
2.函数在上的单调性是( )
A.单调递增
B.单调递减
C.在上单调递减,在上单调递增
D.在上单调递增,在上单调递减
答案:C
解析:由已知得函数的定义域为,,令,得;令,得,函数在上单调递减,在上单调递增.
3.已知定义在上的函数的导函数,且,则实数m的取值范围为__________.
答案:
解析:因为,所以函数在上单调递增,所以,解得.
4.若函数在区间上具有单调性,则a的取值范围是______
答案:
解析:,函数在区间上具有单调性等价于或在上恒成立,则或,即或.
4、小结作业
小结:本节课学习了函数的单调性与导数的关系,判断函数单调性的步骤以及函数的变化快慢与导数的关系.
作业:完成本节课课后习题.
四、板书设计
5.3.1 函数的单调性
1.函数的单调性与导数的关系:一般地,函数的单调性与导函数的正负之间具有如下的关系:在某个区间上,如果,那么函数在区间上单调递增;在某个区间上,如果,那么函数在区间上单调递减.
2.判断函数的单调性的步骤:
第1步,确定函数的定义域;
第2步,求出导数的零点;
第3步,用的零点将的定义域划分为若干个区间,列表给出在各区间上的正负,由此得出函数在定义域内的单调性.
3.函数的变化快慢与导数的关系:一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.
