5.3.1 函数的单调性(课件)(共33张PPT)-高中数学人教A版(2019)选择性必修第二册(共33张PPT)
文档属性
| 名称 | 5.3.1 函数的单调性(课件)(共33张PPT)-高中数学人教A版(2019)选择性必修第二册(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 10:43:41 | ||
图片预览







文档简介
(共33张PPT)
第五章 一元函数的导数及其应用
5.3.1 函数的单调性
高中数学人教A版(2019)选择性必修第二册
学习目标
1.结合实例,借助几何理解可导函数的单调性与其导数的关系.
2.能根据导数判断函数的单调性以及求解函数的单调区间.
3.能够利用函数的单调性解决有关问题.
4.体会导数法判断函数的单调性的优越性.
探索新知
1.函数的单调性与导数的关系
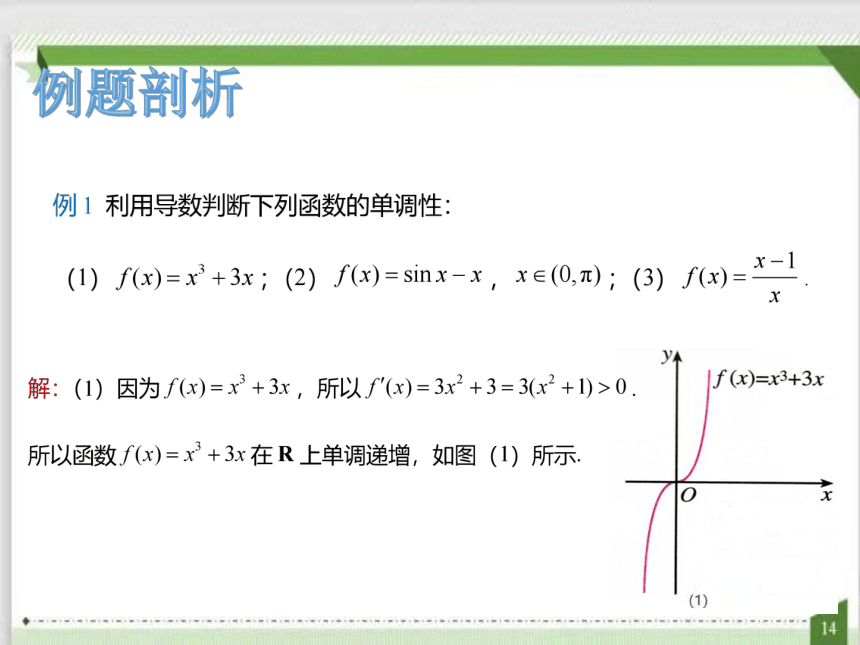
例题剖析
2.三次函数的单调性
判断函数y=f(x)的单调性的步骤
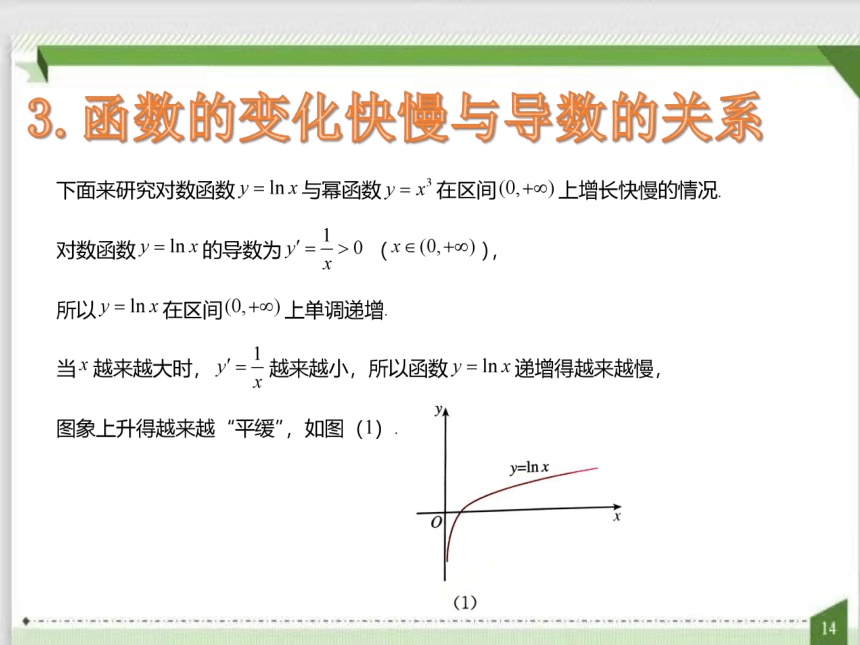
3.函数的变化快慢与导数的关系
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.
例题剖析
课堂小练
课堂小结:
你学到了那些新知识呢?
本节课学习了函数的单调性与导数的关系,判断函数单调性的步骤以及函数的变化快慢与导数的关系.
f(x)=x3+3x
x
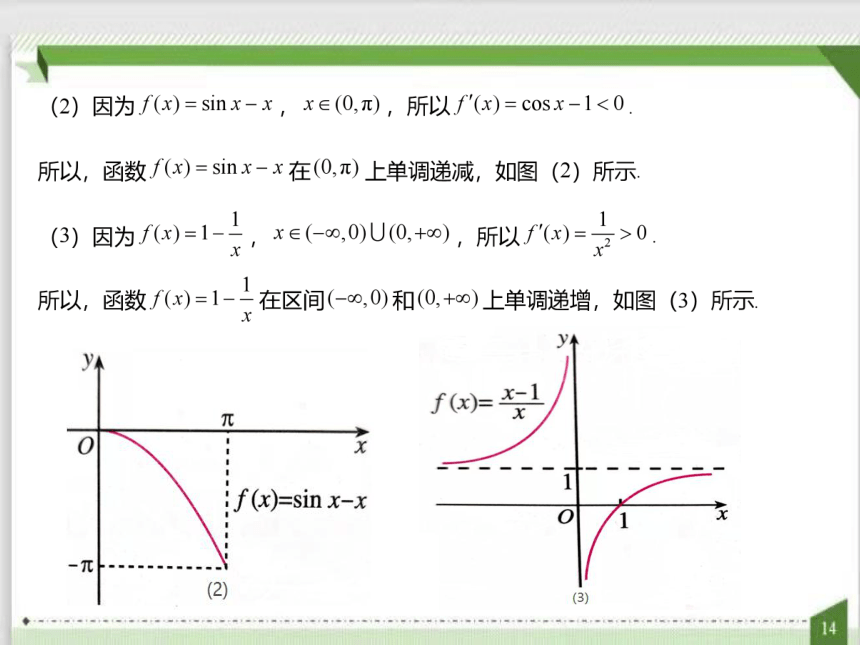
f(=sinx-x
T
(2
f(x)=x-1
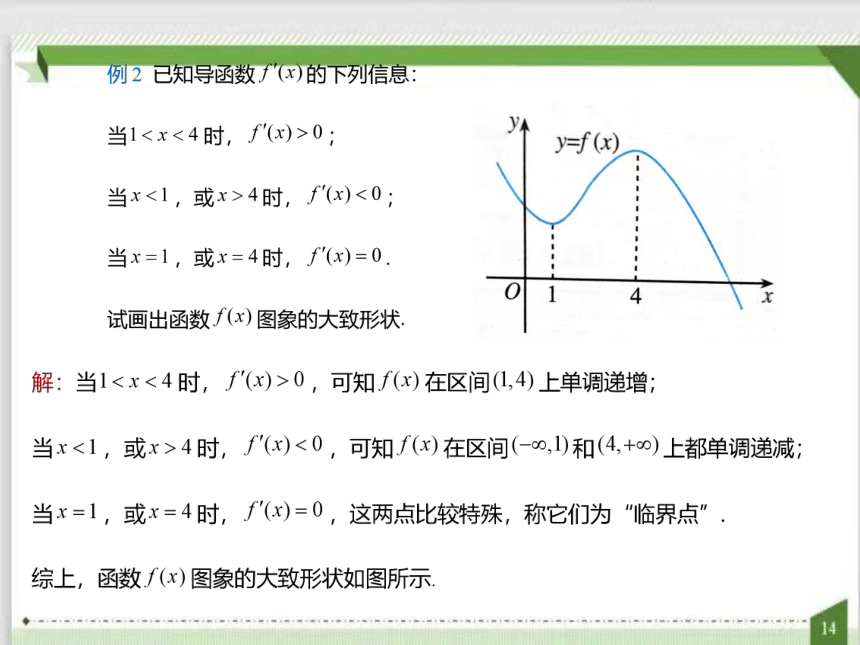
y=f(x)
4
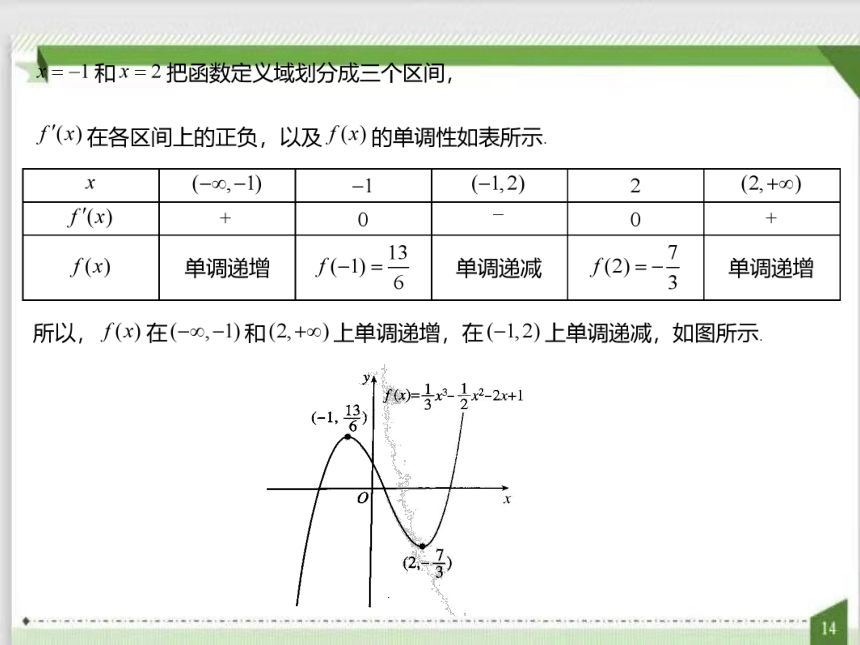
表5.3-1
1,2)
0
f(x)
单调递增f(-1)
单调递减
所以,f(x)在(-∞,-1)和(2,+∞)上单调递
3-6所示
f()
图5.3-6
般情况下,我们可以通过如下步骤判断函数y
y-
Inx
(1)
两数y=1nx的导数为y
0(x∈(0
.当x越来越大时,y=越来越小,所以函数y=1nx递增得越来
或来越“平缓”(如图5.3-7(1))
(1)
(2)
图5.3-7
元函数的导数及其应用
y
函数.在
峭”;在
平缓
图5.3-8
8中的
第五章 一元函数的导数及其应用
5.3.1 函数的单调性
高中数学人教A版(2019)选择性必修第二册
学习目标
1.结合实例,借助几何理解可导函数的单调性与其导数的关系.
2.能根据导数判断函数的单调性以及求解函数的单调区间.
3.能够利用函数的单调性解决有关问题.
4.体会导数法判断函数的单调性的优越性.
探索新知
1.函数的单调性与导数的关系
例题剖析
2.三次函数的单调性
判断函数y=f(x)的单调性的步骤
3.函数的变化快慢与导数的关系
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.
例题剖析
课堂小练
课堂小结:
你学到了那些新知识呢?
本节课学习了函数的单调性与导数的关系,判断函数单调性的步骤以及函数的变化快慢与导数的关系.
f(x)=x3+3x
x
f(=sinx-x
T
(2
f(x)=x-1
y=f(x)
4
表5.3-1
1,2)
0
f(x)
单调递增f(-1)
单调递减
所以,f(x)在(-∞,-1)和(2,+∞)上单调递
3-6所示
f()
图5.3-6
般情况下,我们可以通过如下步骤判断函数y
y-
Inx
(1)
两数y=1nx的导数为y
0(x∈(0
.当x越来越大时,y=越来越小,所以函数y=1nx递增得越来
或来越“平缓”(如图5.3-7(1))
(1)
(2)
图5.3-7
元函数的导数及其应用
y
函数.在
峭”;在
平缓
图5.3-8
8中的
