实数分类
图片预览






文档简介
(共18张PPT)
人教版·数学·八年级(上)
把下列各数写成小数的形式,你有什么发现?
事实上,任何一个有理数都可以写成有限小数或 无限循环小数。
反过来,任何有限小数或无限循环小数也都是 有理数
想一想:除了有限小数和无限循环小数,还有什么其它类型的小数吗?
无限不循环的小数
------叫做无理数
1.圆周率 及一些含有 的数
无理数的特征:
=3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949 …
2.开方开不尽数
=1.7320508075688772935274463415058723669428052538103806280558069794519330169088000370811461867572485756756261414154067030299699450949989524788116555120943736485280932319023055820679748201010846749232650153123432669033228866506722546689218379712270471316603678615880190499865373798593894676503475065760507566183481296061009476021871903250831458295239598329977898245082887144638329173472241639845878553976679580638183536661108431737808943783161020883055249016700235207111442886959909563657970871684980728 …
1.圆周率 及一些含有 的数
2.开方开不尽数
3.有一定的规律,但
不循环的无限小数
无理数的特征:
注意:带根号的数不一定都是无理数
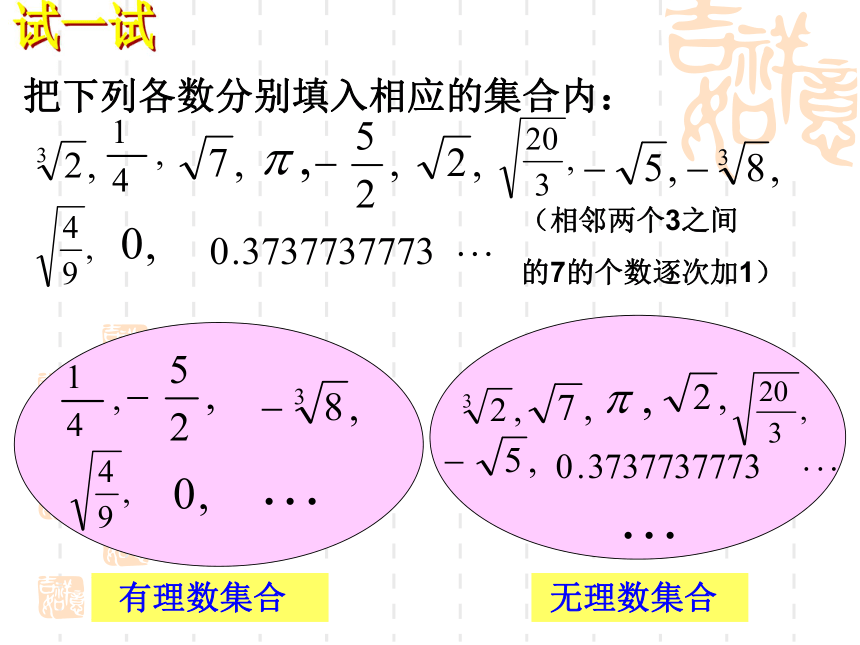
把下列各数分别填入相应的集合内:
(相邻两个3之间
的7的个数逐次加1)
有理数集合
无理数集合
有理数和无理数统称
实数
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
实数的分类(按性质):
1.圆周率 及一些含有 的数
2.开方开不尽数
3.有一定的规律,但不循环的无限小数
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
也可以这样来分类(按符号):
随堂练习
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
7.两个无理数之和一定是无理数。( )
×
×
×
二、把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)负数集合:
(5)分数集合:
(6)实数集合:
0
1
2
4
3
-1
-2
π
直径为1的圆
每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点来表示呢?
你能在数轴上找到表示 这样的无理数的点吗?
问题:边长为1的正方形,对角线长为多少
-2
-1
0
1
2
-
归纳: 与数轴上的点是一一对应的.
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示 .
实数
有序数对和平面直角坐标系中的点有什么关系呢?
-2
-1
0
1
2
-1
1
( ,1)
x
y
A
B
C
有序实数对
( , 1)
( , )
试说出A、B、C三点的坐标
( , )
归纳:平面直角坐标系中的点与 是一一对应的.
有序实数对
-
3.实数与数轴上的点是什么关系.
2.实数的定义和分类
1.无理数的定义
4.平面直角坐标系中的点与有序实数对是什么关系.
课堂小结:
——无限不循环小数叫做无理数。
——按性质分类、按符号分类。
——实数与数轴上的点是一一对应关系。
——有序实数对与平面直角坐标系上的点是一一对应关系。
1、请将数轴上是各点与下列实数对应起来.
-3 -2 -1 0 1 2 3 4
A
B
C
D
E
2、学习检测P40第1—11题.
人教版·数学·八年级(上)
把下列各数写成小数的形式,你有什么发现?
事实上,任何一个有理数都可以写成有限小数或 无限循环小数。
反过来,任何有限小数或无限循环小数也都是 有理数
想一想:除了有限小数和无限循环小数,还有什么其它类型的小数吗?
无限不循环的小数
------叫做无理数
1.圆周率 及一些含有 的数
无理数的特征:
=3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949 …
2.开方开不尽数
=1.7320508075688772935274463415058723669428052538103806280558069794519330169088000370811461867572485756756261414154067030299699450949989524788116555120943736485280932319023055820679748201010846749232650153123432669033228866506722546689218379712270471316603678615880190499865373798593894676503475065760507566183481296061009476021871903250831458295239598329977898245082887144638329173472241639845878553976679580638183536661108431737808943783161020883055249016700235207111442886959909563657970871684980728 …
1.圆周率 及一些含有 的数
2.开方开不尽数
3.有一定的规律,但
不循环的无限小数
无理数的特征:
注意:带根号的数不一定都是无理数
把下列各数分别填入相应的集合内:
(相邻两个3之间
的7的个数逐次加1)
有理数集合
无理数集合
有理数和无理数统称
实数
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
实数的分类(按性质):
1.圆周率 及一些含有 的数
2.开方开不尽数
3.有一定的规律,但不循环的无限小数
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
也可以这样来分类(按符号):
随堂练习
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
7.两个无理数之和一定是无理数。( )
×
×
×
二、把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)负数集合:
(5)分数集合:
(6)实数集合:
0
1
2
4
3
-1
-2
π
直径为1的圆
每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点来表示呢?
你能在数轴上找到表示 这样的无理数的点吗?
问题:边长为1的正方形,对角线长为多少
-2
-1
0
1
2
-
归纳: 与数轴上的点是一一对应的.
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示 .
实数
有序数对和平面直角坐标系中的点有什么关系呢?
-2
-1
0
1
2
-1
1
( ,1)
x
y
A
B
C
有序实数对
( , 1)
( , )
试说出A、B、C三点的坐标
( , )
归纳:平面直角坐标系中的点与 是一一对应的.
有序实数对
-
3.实数与数轴上的点是什么关系.
2.实数的定义和分类
1.无理数的定义
4.平面直角坐标系中的点与有序实数对是什么关系.
课堂小结:
——无限不循环小数叫做无理数。
——按性质分类、按符号分类。
——实数与数轴上的点是一一对应关系。
——有序实数对与平面直角坐标系上的点是一一对应关系。
1、请将数轴上是各点与下列实数对应起来.
-3 -2 -1 0 1 2 3 4
A
B
C
D
E
2、学习检测P40第1—11题.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
