人教版八年级数学上册全等三角形导学
文档属性
| 名称 | 人教版八年级数学上册全等三角形导学 |  | |
| 格式 | zip | ||
| 文件大小 | 179.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-15 20:11:34 | ||
图片预览




文档简介
课题: 11.1 全等三角形
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.知道什么是全等形、全等三角形及全等三角形的对应元素,会用符号正确地表示两个三角形全等.
2.知道全等三角形的性质,并会进行应用.
3.能熟练找出两个全等三角形的对应角、对应边.
【自学指导】
活动一 知道全等形、全等三角形
将三角板按在纸上,沿外框画出两个三角形,把这两个三角形裁下来后放在一起,观察它们能否重合。
2.观看课本美丽的图片并阅读课本P2 的部分,思考并回答下列问题:
(1)什么是全等形?什么是全等三角形?你能举出生活中全等形的实例吗?
活动二 知道全等三角形对应元素, 会用符号表示全等全等三角形,知道全等三角形的性质
1.阅读课本P3 的部分,思考并回答下列问题:
(1).思考: 图11.1_1,11.1_2,11.1_3中的两个三角形全等吗?为什么?如果全等把它们分别表示出来.(注意书写时对应顶点字母写在对应的位置上)
(2).寻找图11.1_1,11.1_2,11.1_3中两个全等三角形的对应元素,它们的对应边有什么关系?对应角呢?
【展示知识点】
1.________相同的图形放在一起能够____。这样的两个图形叫做____。
2.能够_____的两个三角形叫做全等三角形。
3.一个图形经过__、__、__后位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形____
4.______叫做对应顶点。_______叫做对应边。_____叫做对应角。
5.全等三角形有这样的性质: 对应边 ,对应角 。
【知识应用】
1.如图,△OCA≌△OBD,C和B,A和D是对应顶点,说出这两个三角形中相等的边和角.
2.小组讨论交流寻找对应角、对应边的经验 : .
3.如图,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.
【检测反馈,巩固提高】
1.如右图,将△ABC沿直线BC平移,得到△DEF
(1)线段AB、DE是对应线段吗?有什么关系?线段AC和DF呢?
(2)线段BE和CF有什么关系?为什么?
(3) 若∠A=50 ,∠B=30 ,你知道其他各角的度数吗?为什么?
2.如图,△ABC≌△DEC,CA和CD,CB和CE是对应边,∠ACD
和∠BCE相等吗?为什么?
【课后反思】
我的问题:
我的小组问题:
课题:11.2三角形全等的判定(第一课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.理解“边边边”的内容,会运用“SSS”证明三角形全等,为证明线段相等或角相等创造条件;
2、初步体会尺规作图
3、掌握简单的证明格式。
【自学指导】
活动一 探索三角形全等的条件
1.只给一个条件:(1)画出一条边为6cm 三角形 (2) 画出一个角为30度的三角形.小组交流所画的三角形全等吗?
2.给出两个条件画三角形时,有几种可能的情况?分别按照下面条件,用刻度尺或量角器画三角形,并和小组的同学比较一下,所画的图形全等吗
①三角形的一个内角为60°,一条边为3 cm; ② 三角形的两个内角分别为30°和70°;
③ 三角形的两条边分别为3 cm和5 cm
从1、2画图归纳:如果只知道两个三角形有一个或两个部分(边或角)对应相等,那么这两个三角形____(填“一定”或 “不一定”)全等。
3.若给出三个条件画三角形,你能说出有几种可能的情况吗?(小组讨论交流)
4. 小组讨论P6探究2,交流合作,初步体会尺规作图(具体按P7画图步骤)
【展示知识点】
由活动我们得到:
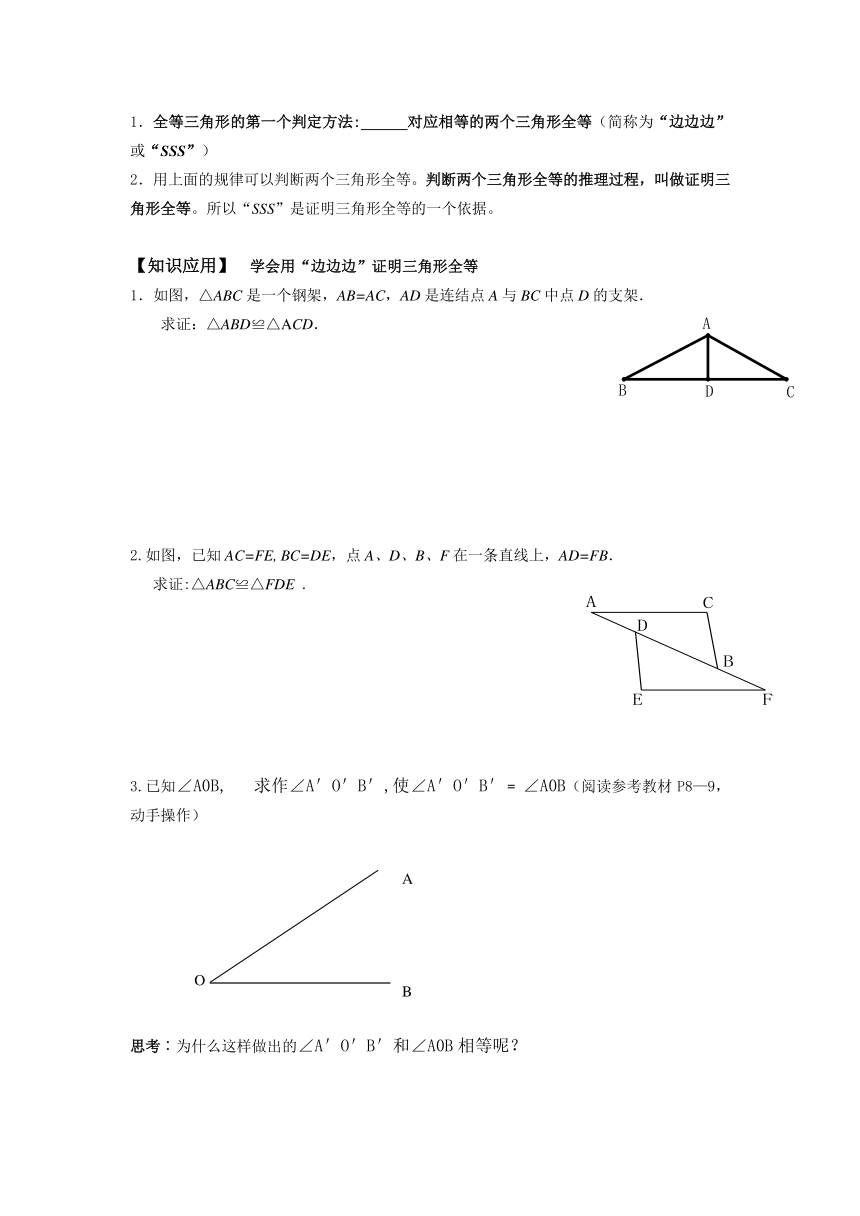
1.全等三角形的第一个判定方法: 对应相等的两个三角形全等(简称为“边边边”或“SSS”)
2.用上面的规律可以判断两个三角形全等。判断两个三角形全等的推理过程,叫做证明三角形全等。所以“SSS”是证明三角形全等的一个依据。
【知识应用】 学会用“边边边”证明三角形全等
1.如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
2.如图,已知AC=FE, BC=DE,点A、D、B、F在一条直线上,AD=FB.
求证:△ABC≌△FDE .
3.已知∠A0B, 求作∠A'O'B',使∠A'O'B'﹦∠A0B(阅读参考教材P8—9,动手操作)
思考︰为什么这样做出的∠A'O'B'和∠A0B相等呢?
【检测反馈,巩固提高】
1. 教材P8,练习
2.如图,四边形ABCD中,AD=CB,AB=CD.
求证: ① △ABC≌△CDA.
② AB‖CD
【课后反思】
我的问题:
我的小组问题:
课题:11.2三角形全等的条件(第二课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1、会画一个三角形与已知三角形全等(根据两边与夹角对应相等)
2.知道三角形全等“边角边”的内容.
3.会运用“SAS”识别三角形全等,为证明线段相等或角相等创造条件.
4、探究具备“SSA”条件的两个三角形是否全等?
【自学指导】
活动一 探索三角形全等的条件(两边及夹角)
1.认真阅读课本第8-9页的探究3内容,小组合作学习,注意画图时的规范,用尺规作图注意画法。
通过画图发现规律:___________的两个三角形全等。
活动二 探索具备“两边及其中一边的对角”对应相等的两个三角形是否全等
2.画一画:三角形的两条边分别为4cm和3cm,长度为3cm的边所对的角为30 °,画出这个三角形,把你画的三角形与其他同学画的三角形进行比较,由此你发现了什么?把你的发现和同伴交流。
通过画图发现规律:如果“两边及其中一边的对角对应相等,那么这两个三角形____(填“一定”或 “不一定”)全等。
【展示知识点】
由活动我们得到:
1.全等三角形的第二个判定方法: 对应相等的两个三角形全等(简称为“边角边”或“SAS”)
2.两边及一边的对角对应相等的两个三角形不一定全等,即:不存在“边边角”这个判定定理。
(注意:在以后使用两边一角证明三角形全等时,一定要审清是否符合“边角边”这个判定定理。)
【知识应用】 学会用“边角边”证明三角形全等
1.如图,已知AD∥BC,AD=CB.求证:△ABC≌△CDA.
(提示:要证明两个三角形全等,已具有两个条件,一是AD=CB(已知),二是___________,还能再找一个条件吗?可以小组交流后再完成)
证明:
2、认真阅读学习教材P9例2。我们得到:在证明两个三角形中线段相等或角相等时通常通过证明_________来解决。
【检测反馈,巩固提高】
1.如图,已知AB=AC,AD=AE,∠1=∠2.
求证:△ABD≌△ACE.
2.已知:点A、F、E、C在同一条直线上, AF=CE,BE∥DF,BE=DF.
求证:AB∥CD
3、如图3要测量工件内槽宽,可以把两根钢条的中点连在一起,做成一个工具,只要测量出__的长,就是内槽的宽,为什么?
图3
4、如图AB=AC,AD=AE,求证:(1)∠B=∠C (2) ∠BDC=∠BEC
【课后反思】
我的问题:
我的小组问题:
课题:11.2三角形全等的条件(第3课时)
班级: 组名: 姓名: 创作人: 使用时间:
【学习目标】
1.知道三角形全等“角边角”的内容.
2.会运用“ASA”识别三角形全等,为证明线段相等或角相等创造条件
【自学指导】
活动一 探索三角形全等的条件(角边角)
1.画一画:如图,△ABC是任意一个三角形,画△A1B1C1 ,使A1B1=AB,
∠A1=∠A,∠B1=∠B,把画的△A1B1C1剪下来放在△ABC进行比较,它
们是否重合?由此你能得出什么结论?
【展示知识点】
由活动我们得到:
全等三角形的第三个判定方法: 对应相等的两个三角形全等(简称“角边角”或“ASA”)
【知识应用】 学会用“角边角”证明三角形全等
如图,已知∠ABC=∠D,∠ACB=∠CBD,判断图中的两个三
角形是否全等,如果全等请说明理由.如果不全等,可以改变什么
条件可使这两个三角形全等。
如图,已知点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证:AD=AE
3.如图,已知 AB∥CD,CE∥BF. 若AE=DF,
求证:BF=CE
【检测反馈,巩固提高】
1.如图1,小明把一块三角形的玻璃打碎成了三块,现在要到玻璃店
去配一块完全一样的玻璃,那么最省事的办法( )
A、选①去, B、选② C、选③去
2.如图2,O是AB的中点, 要使通过角边角(ASA)来判定
△OAC≌△OBD,需要添加一个条件,下列条件正确的是( )
A、∠A=∠B B、AC=BD C、∠C=∠D
3.如右图,已知∠1=∠2,∠3=∠4,AB与CD相等吗?
请你说明理由.
4.如图,要测量河两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再定出BF 的垂线DE,使A,C,E在一条直线上,这时测得DE的长度就是AB的长度,为什么?
【课后反思】
我的问题:
我的小组问题:
课题:11.2三角形全等的条件(第4课时)
班级: 组名: 姓名: 创作人: 使用时间:
【学习目标】
1.知道“角角边”内容.
2.利用“AAS”证明全等,为证明线段相等和角相等创造条件.
【自学指导】
活动一 探索三角形全等的条件
1.在“角边角”中,边是两个角的夹边,如果边是其中一个角的对边,那么这两个三角形还全等吗?
画一画:先任意画一个△ABC,再画一个△A1B1C1,使∠A1=∠A,∠B1=∠B,B1C1=BC,把你画好的△A1B1C1剪下,放到△ABC上,它们全等吗
2 .阅读P11—12探究6,并试着独立表达证明过程.
【展示知识点】
由活动我们得到:
1 .全等三角形的第四个判定方法: 对应相等的两个三角形全等(简称“角角边”或“AAS”)
2 .全等三角形的四种判定方法是: .
3 .要判定两个三角形全等,至少具备 已知条件,且这 个条件中至少有一个条件是一组边相等.
【知识应用】
1.如图,已知∠ADB=∠ADC,由AAS判定△ABD≌△ACD,
还需添加的一个条件是____________.(说说你是怎么想的)
2.已知AB//DE,且AB=DE,
(1)请你只添加一个条件,使△ABC≌△DEF,你添加的条件是
(2)选其中的一种方法进行证明.
【检测反馈,巩固提高】(第3,第4题选作一道)
1.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是 ( )A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
2.如果∠B=∠C,AD平分∠BAC,证明:△ABD≌△ACD
3.如图:在△ABC,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F,
利用学过的知识你能证明几对三角形全等?选一对全等加以证明.
4.如图:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足为C,D。
求证:(1)OC=OD,(2)DF=CF
【课后反思】
我的问题: 我的小组问题:
课题:11.2三角形全等的判定(第5课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2.知道直角三角形全等的条件,并能加以应用.
【自学指导】
活动一
问题1:前面学习的判定方法,直角三角形是否还能用?
2:一个锐角和一条边对应相等的两个直角三角形全等吗 为什么
3:两条直角边对应相等的两个直角三角形全等吗 为什么
4:斜边和一条直角边对应相等的两个直角三角形一定全等吗 为什么
活动二 探究斜边和一条直角边对应相等的两个直角三角形是否全等
阅读教材P13—14探究8,并与同学动手操作作图过程。
思考:从中你发现了什么?(与同学交流你的发现)
【展示知识点】
由活动我们得到:
1.直角三角形的特殊判定定理 的两个直角三角形全等(简称“斜边,直角边”或“HL”)
2.归纳:在什么条件下,两个直角三角形一定全等
①
②
【知识应用】
阅读教材P14例4,完成以下练习
1.如图1,△ABC中,AB=AC,AD是高,则△ADB与△ADC (填“全等”或“不全等” ),根据 (用简写法).
2.判断两个直角三角形全等的条件不正确的是( )
A. 两条直角边对应相等 B. 斜边和一锐角对应相等
C. 斜边和一条直角边对应相等 D. 两个锐角对应相等
3.如图2,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由.
【检测反馈,巩固提高】
如图AB=CD,AE⊥BC,DF⊥BC,CE=BF
求证:(1)AE=DF
(2)CD∥AB
2、△ABC中,AB=AC,M为BC中点,MD⊥AB于D,ME⊥AC于E,求证:MD=ME
【课后反思】
我的问题:
我的小组问题:
课题:11.2三角形全等的判定(第6课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.知道三角形全等的各种判断方法;
2.能根据具体问题合理选择相应的判断方法.
【活动流程】
归纳判断三角形全等的条件
1.填下表:(挂出小黑板,让学生思考、讨论,共同填答).
两个三角形中对应相等的元素 两个三角形是否全等 反例(可画图)
SSS
SAS
SSA
ASA
AAS
AAA
活动二 应用全等判断定理解题
1.如图,AB∥CD,AD∥BC,AC、BD相交于点O.
(1)由AD∥BC,可得 = ,由AB∥CD,
可得 = ,又由 ,于是△ABD≌△CDB;
(2)由△ABD≌△CDB ,可得AD= ,AB= ,
从而还可证明 △AOD≌ ;△AOB≌ .
(3)图中全等三角形共有 对,分别用了哪些判断方法
2.如图,除公共边AB外,根据下列括号内三角形全等的条件,
在横线上添加适当的条件,使△ABC与△ABD全等:
(1) , (SSS);(2) , (ASA);
(3)∠1=∠2 , (SAS);(4) ,∠3=∠4 (AAS).
3.下列各说法中,正确的是( )
A.有两边和一角对应相等的两个三角形全等 B.有两角一边分别相等的两个三角形全等
C.两个锐角对应相等的两个直角三角形全等 D.有两组边相等且周长相等的两个三角形全等
4.如图,已知:AE=CF,AD∥BC,AD=CB. 求证:△ADF≌△ CBE .
5.已知:如图,∠ACB=∠ADB=90°,AC=AD,E在AB上.求证CE=DE.
6.如图,AD与BC相交于O,OC=OD,OA=OB.求证:
7.如图,D,E,F,B在一条直线上,AB=CD,∠B=∠D,BF=DE,
求证:(1)AE=CF ;(2)AE∥CF
课题:11.3角的平分线的性质(第1课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1、会用尺规作图作角平分线;(会说作法)
2、理解并掌握角平分线的性质
3、感受证明一个几何命题的方法与步骤
【自学指导】
活动一 学会作角平分线
自学课本19页(10分钟)
说出探究中AE是∠DAE的平分线的理由
2、 动手操作,作一个角的角平分线
已知:∠AOB.
求作:∠AOB的平分线.
作法:(1)
(2)
(3)
(注意: 角的平分线是一条射线,它不是线段,也不是直线.)
活动二 探究角平分线的性质
阅读课本P20—21,动手操作完成课本第20页的探究。
思考:角平分线上的点到角两边的距离大小关系如何?你能得到什么猜想?把你的猜想写出来。
2.你能证明自己的猜想是正确的吗?试一试。
3.你能结合右图用符号语言表示角平分线的性质吗?
【展示知识点】
⑴ 用尺规怎样画角的平分线_________
⑵角平分线的性质:角的平分线上的点_________
⑶证明几何命题的步骤有_________ _________ _________
【知识应用】
已知∠AOB的角平分线OC,点P在OC上,且点P到OA的距离为4cm,则点P到边OB的距离是__
如图2在△ABC中,∠C=900,AD平分∠BAC,BC=10cm,BD=6cm,
则点D到AB的距离为______
如右图, △ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,
DF⊥AC,垂足分别为E、F. 求证EB=FC .
【检测反馈,巩固提高】
已知△ABC内,∠ABC,∠ACB的角平分线交于点P,且PD、PE、PF分别垂直于BC、AC、AB于D、E、F三点,求证:PD=PE=PF
2.如右图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2.
求:(1)点D到AB的距离;
(2)△ABD的面积.
【课后反思】
我的问题: 我的小组问题:
课题:11.3角的平分线的性质(第2课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.知道角平分线性质定理的逆定理,并会进行应用;
2.注意区别这两个定理的条件和结论,熟练用来解题.
【自学指导】
活动一 复分线的性质定理
1.角平分线性质定理的内容是什么?
如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
(先独立思考解答,然后在组内交流。)
想一想:我们知道: 角平分线上的点到 距离相等;那么到角两边距离相等的点是否也在这个角平分线上呢?
活动二 探究角平分线性质定理的逆命题
1.阅读教材P21 思考,并说明理由。
求证:到角的两边的距离相等的点在角的平分线上(画出图形,写出已知和求证,再加以证明).
【展示知识点】
角平分线性质定理的逆定理:角的内部到角两边距离相等的点_________
【知识应用】角平分线性质定理的逆定理的应用
1.如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,OB=OC.
求证:∠OAB=∠OAC.
【检测反馈,巩固提高】
已知△ABC的外角平分线BD、CE相交于点P . 求证:点P在∠A 的平分线上
2.如图:在△ABC中,∠B=∠C=50°,D是BC的中点,DE⊥AB,DF⊥AC,求∠BAD的度数.
【课后反思】
我的问题:
我的小组问题:
全等三角形复习课 (第1课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.总结三角形全等的识别条件,灵活运用各种判定方法解决问题;
2.培养逻辑思维能力,发展基本的创新意识和能力。
【活动方案】
活动一 填一填,算一算,看谁做得既对又快
1.已知如图(1),≌,其中的对应边:____与____,____与____,____与____,两个全等三角形中对应角有
2.如图(2), ≌,BC的延长线交DA于F,交DE于G, ∠ACB=105 , ∠CAD=10 , ∠D=25 . 求﹦ 、﹦
3.如图(3),在△ABD和△ACE中,有下列论断:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE.请以其中三个论断作为条件,另一个论断作为结论,写出一个真命题:
4. 对于△ABC与△DEF,已知∠A=∠D,∠B=∠E,则下列条件①AB=DE;②AC=DF;③BC=DF;④AB=EF中,能判定它们全等的有( )
A.①② B.①③ C.②③ D.③④
5.下列说法正确的是( )
A.面积相等的两个三角形全等 B.周长相等的两个三角形全等
C.三个角对应相等的两个三角形全等 D.能够完全重合的两个三角形全等
6. 下列数据能确定形状和大小的是( )
A.AB=4,BC=5,∠C=60° B.AB=6,∠C=60°,∠B=70°
C.AB=4,BC=5,CA=10 D.∠C=60°,∠B=70°,∠A=50°
7. 在△ABC和△DEF中,∠A=∠D,AB = DE,添加下列哪一个条件,依然不能证明△ABC≌△DEF( )
A.AC = DF B.BC = EF C.∠B=∠E D.∠C=∠F
思考并交流:在找全等三角形的对应边和对应角时,如何做到对应?
活动二 应用知识,解决问题
如图,在中,,D、E分别为AC、AB上的点,且AD=BD,AE=BC,DE=DC.
求证:DE⊥AB
2.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.求证:AD是△ABC的角平分线.
【检测反馈,巩固提高】
1.如图,图(1)中等腰△ABC与等腰△DEC共点于C,且∠BCA=∠ECD,连结BE,AD,若BC=AC、EC=DC.求证:BE=AD;若将等腰△EDC绕点C旋转至图(2)(3)(4)情况时,其余条件不变,BE与AD还相等吗?为什么
【课后反思】
我的问题: 我的小组问题:
全等三角形复习课(第2课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.会综合运用全等三角形的性质和判定解题;
2.增强观察和理解能力,几何语言的叙述能力及运用全等知识解决实际问题的能力.
【活动方案】
活动一 熟练选用确当的方法证明三角形全等
1.将两根钢条AA/、BB/中点O连在一起,使AA/、BB/绕着点O自由转动,做成一个测量工具,则A/B/的长等于内槽宽AB,判定△OAB≌△OA/B/ 的理由是 .
2.已知AB//DE,且AB=DE,
(1)请你只添加一个条件,使△ABC≌△DEF,你添加的条件是
(2)选其中的一种方法进行证明.
第2题 第3题
3.如图所示,在△ABC和△ABD中,∠C=∠D=90°, 要使△ABC≌△ABD, 还需增加一个条件是__________,请利用你所增加的条件加以证明.
4. 如图,∠1=∠2,∠E=∠A,EC=DA,则△ABD≌△EBC时,运用的判定定理是( )
A.SSS B.ASA C.AAS D.SAS
5. 如图,若线段AB,CD交于点O,且AB、CD互相平分,则下列结论错误的是( )
A.AD=BC B.∠C=∠D C.AD∥BC D.OB=OC
6. 如图,AE⊥BD于E,CF⊥BD于F,AB = CD,AE = CF,
则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
7.如图,DE⊥BC,BE=EC,且AB=5,AC=8,
则△ABD的周长为( )
A.21 B.18 C.13 D.9
8.已知AC//BD,∠CAB和∠DBA的平分线EA、EB与CD相交于点E.
求证:AB=AC+BD.(提示:在AB上截取AF=AC)
【检测反馈,巩固提高】
如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N。
(1)求证:MN=AM+BN。
(2) 若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,
则AM、BN与MN之间有什么关系?请说明理由。
_
D
_
C
_
A
_
B
_
E
A
O
B
A
B
S
D
C
C
B
E
D
A
图4
A
C
D
B
D
A
B
C
A
B
D
C
图1
图2
A
B
C
3
4
1
2.如图,除公共边AB外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使△ABC与△ABD全等:
(1) , (SSS);(2) , (ASA);
(3)∠1=∠2 , (SAS);(4) ,∠3=∠4 (AAS).
2
D
A
E
C
D
B
C
D
E
F
A
B
B
C
(图3)
A
D
E
图1
图2
图(2)
B
E
C
A
F
D
(1)
(2)
(3)
(4)
B
C
A
D
B
A
C
E
D
(第4题)
2
1
O
A
D
C
B
(第5题)
(第6题)
A
D
C
B
E
F
E
B
A
D
C
(第7题)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.知道什么是全等形、全等三角形及全等三角形的对应元素,会用符号正确地表示两个三角形全等.
2.知道全等三角形的性质,并会进行应用.
3.能熟练找出两个全等三角形的对应角、对应边.
【自学指导】
活动一 知道全等形、全等三角形
将三角板按在纸上,沿外框画出两个三角形,把这两个三角形裁下来后放在一起,观察它们能否重合。
2.观看课本美丽的图片并阅读课本P2 的部分,思考并回答下列问题:
(1)什么是全等形?什么是全等三角形?你能举出生活中全等形的实例吗?
活动二 知道全等三角形对应元素, 会用符号表示全等全等三角形,知道全等三角形的性质
1.阅读课本P3 的部分,思考并回答下列问题:
(1).思考: 图11.1_1,11.1_2,11.1_3中的两个三角形全等吗?为什么?如果全等把它们分别表示出来.(注意书写时对应顶点字母写在对应的位置上)
(2).寻找图11.1_1,11.1_2,11.1_3中两个全等三角形的对应元素,它们的对应边有什么关系?对应角呢?
【展示知识点】
1.________相同的图形放在一起能够____。这样的两个图形叫做____。
2.能够_____的两个三角形叫做全等三角形。
3.一个图形经过__、__、__后位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形____
4.______叫做对应顶点。_______叫做对应边。_____叫做对应角。
5.全等三角形有这样的性质: 对应边 ,对应角 。
【知识应用】
1.如图,△OCA≌△OBD,C和B,A和D是对应顶点,说出这两个三角形中相等的边和角.
2.小组讨论交流寻找对应角、对应边的经验 : .
3.如图,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.
【检测反馈,巩固提高】
1.如右图,将△ABC沿直线BC平移,得到△DEF
(1)线段AB、DE是对应线段吗?有什么关系?线段AC和DF呢?
(2)线段BE和CF有什么关系?为什么?
(3) 若∠A=50 ,∠B=30 ,你知道其他各角的度数吗?为什么?
2.如图,△ABC≌△DEC,CA和CD,CB和CE是对应边,∠ACD
和∠BCE相等吗?为什么?
【课后反思】
我的问题:
我的小组问题:
课题:11.2三角形全等的判定(第一课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.理解“边边边”的内容,会运用“SSS”证明三角形全等,为证明线段相等或角相等创造条件;
2、初步体会尺规作图
3、掌握简单的证明格式。
【自学指导】
活动一 探索三角形全等的条件
1.只给一个条件:(1)画出一条边为6cm 三角形 (2) 画出一个角为30度的三角形.小组交流所画的三角形全等吗?
2.给出两个条件画三角形时,有几种可能的情况?分别按照下面条件,用刻度尺或量角器画三角形,并和小组的同学比较一下,所画的图形全等吗
①三角形的一个内角为60°,一条边为3 cm; ② 三角形的两个内角分别为30°和70°;
③ 三角形的两条边分别为3 cm和5 cm
从1、2画图归纳:如果只知道两个三角形有一个或两个部分(边或角)对应相等,那么这两个三角形____(填“一定”或 “不一定”)全等。
3.若给出三个条件画三角形,你能说出有几种可能的情况吗?(小组讨论交流)
4. 小组讨论P6探究2,交流合作,初步体会尺规作图(具体按P7画图步骤)
【展示知识点】
由活动我们得到:
1.全等三角形的第一个判定方法: 对应相等的两个三角形全等(简称为“边边边”或“SSS”)
2.用上面的规律可以判断两个三角形全等。判断两个三角形全等的推理过程,叫做证明三角形全等。所以“SSS”是证明三角形全等的一个依据。
【知识应用】 学会用“边边边”证明三角形全等
1.如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
2.如图,已知AC=FE, BC=DE,点A、D、B、F在一条直线上,AD=FB.
求证:△ABC≌△FDE .
3.已知∠A0B, 求作∠A'O'B',使∠A'O'B'﹦∠A0B(阅读参考教材P8—9,动手操作)
思考︰为什么这样做出的∠A'O'B'和∠A0B相等呢?
【检测反馈,巩固提高】
1. 教材P8,练习
2.如图,四边形ABCD中,AD=CB,AB=CD.
求证: ① △ABC≌△CDA.
② AB‖CD
【课后反思】
我的问题:
我的小组问题:
课题:11.2三角形全等的条件(第二课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1、会画一个三角形与已知三角形全等(根据两边与夹角对应相等)
2.知道三角形全等“边角边”的内容.
3.会运用“SAS”识别三角形全等,为证明线段相等或角相等创造条件.
4、探究具备“SSA”条件的两个三角形是否全等?
【自学指导】
活动一 探索三角形全等的条件(两边及夹角)
1.认真阅读课本第8-9页的探究3内容,小组合作学习,注意画图时的规范,用尺规作图注意画法。
通过画图发现规律:___________的两个三角形全等。
活动二 探索具备“两边及其中一边的对角”对应相等的两个三角形是否全等
2.画一画:三角形的两条边分别为4cm和3cm,长度为3cm的边所对的角为30 °,画出这个三角形,把你画的三角形与其他同学画的三角形进行比较,由此你发现了什么?把你的发现和同伴交流。
通过画图发现规律:如果“两边及其中一边的对角对应相等,那么这两个三角形____(填“一定”或 “不一定”)全等。
【展示知识点】
由活动我们得到:
1.全等三角形的第二个判定方法: 对应相等的两个三角形全等(简称为“边角边”或“SAS”)
2.两边及一边的对角对应相等的两个三角形不一定全等,即:不存在“边边角”这个判定定理。
(注意:在以后使用两边一角证明三角形全等时,一定要审清是否符合“边角边”这个判定定理。)
【知识应用】 学会用“边角边”证明三角形全等
1.如图,已知AD∥BC,AD=CB.求证:△ABC≌△CDA.
(提示:要证明两个三角形全等,已具有两个条件,一是AD=CB(已知),二是___________,还能再找一个条件吗?可以小组交流后再完成)
证明:
2、认真阅读学习教材P9例2。我们得到:在证明两个三角形中线段相等或角相等时通常通过证明_________来解决。
【检测反馈,巩固提高】
1.如图,已知AB=AC,AD=AE,∠1=∠2.
求证:△ABD≌△ACE.
2.已知:点A、F、E、C在同一条直线上, AF=CE,BE∥DF,BE=DF.
求证:AB∥CD
3、如图3要测量工件内槽宽,可以把两根钢条的中点连在一起,做成一个工具,只要测量出__的长,就是内槽的宽,为什么?
图3
4、如图AB=AC,AD=AE,求证:(1)∠B=∠C (2) ∠BDC=∠BEC
【课后反思】
我的问题:
我的小组问题:
课题:11.2三角形全等的条件(第3课时)
班级: 组名: 姓名: 创作人: 使用时间:
【学习目标】
1.知道三角形全等“角边角”的内容.
2.会运用“ASA”识别三角形全等,为证明线段相等或角相等创造条件
【自学指导】
活动一 探索三角形全等的条件(角边角)
1.画一画:如图,△ABC是任意一个三角形,画△A1B1C1 ,使A1B1=AB,
∠A1=∠A,∠B1=∠B,把画的△A1B1C1剪下来放在△ABC进行比较,它
们是否重合?由此你能得出什么结论?
【展示知识点】
由活动我们得到:
全等三角形的第三个判定方法: 对应相等的两个三角形全等(简称“角边角”或“ASA”)
【知识应用】 学会用“角边角”证明三角形全等
如图,已知∠ABC=∠D,∠ACB=∠CBD,判断图中的两个三
角形是否全等,如果全等请说明理由.如果不全等,可以改变什么
条件可使这两个三角形全等。
如图,已知点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证:AD=AE
3.如图,已知 AB∥CD,CE∥BF. 若AE=DF,
求证:BF=CE
【检测反馈,巩固提高】
1.如图1,小明把一块三角形的玻璃打碎成了三块,现在要到玻璃店
去配一块完全一样的玻璃,那么最省事的办法( )
A、选①去, B、选② C、选③去
2.如图2,O是AB的中点, 要使通过角边角(ASA)来判定
△OAC≌△OBD,需要添加一个条件,下列条件正确的是( )
A、∠A=∠B B、AC=BD C、∠C=∠D
3.如右图,已知∠1=∠2,∠3=∠4,AB与CD相等吗?
请你说明理由.
4.如图,要测量河两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再定出BF 的垂线DE,使A,C,E在一条直线上,这时测得DE的长度就是AB的长度,为什么?
【课后反思】
我的问题:
我的小组问题:
课题:11.2三角形全等的条件(第4课时)
班级: 组名: 姓名: 创作人: 使用时间:
【学习目标】
1.知道“角角边”内容.
2.利用“AAS”证明全等,为证明线段相等和角相等创造条件.
【自学指导】
活动一 探索三角形全等的条件
1.在“角边角”中,边是两个角的夹边,如果边是其中一个角的对边,那么这两个三角形还全等吗?
画一画:先任意画一个△ABC,再画一个△A1B1C1,使∠A1=∠A,∠B1=∠B,B1C1=BC,把你画好的△A1B1C1剪下,放到△ABC上,它们全等吗
2 .阅读P11—12探究6,并试着独立表达证明过程.
【展示知识点】
由活动我们得到:
1 .全等三角形的第四个判定方法: 对应相等的两个三角形全等(简称“角角边”或“AAS”)
2 .全等三角形的四种判定方法是: .
3 .要判定两个三角形全等,至少具备 已知条件,且这 个条件中至少有一个条件是一组边相等.
【知识应用】
1.如图,已知∠ADB=∠ADC,由AAS判定△ABD≌△ACD,
还需添加的一个条件是____________.(说说你是怎么想的)
2.已知AB//DE,且AB=DE,
(1)请你只添加一个条件,使△ABC≌△DEF,你添加的条件是
(2)选其中的一种方法进行证明.
【检测反馈,巩固提高】(第3,第4题选作一道)
1.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是 ( )A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
2.如果∠B=∠C,AD平分∠BAC,证明:△ABD≌△ACD
3.如图:在△ABC,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F,
利用学过的知识你能证明几对三角形全等?选一对全等加以证明.
4.如图:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足为C,D。
求证:(1)OC=OD,(2)DF=CF
【课后反思】
我的问题: 我的小组问题:
课题:11.2三角形全等的判定(第5课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2.知道直角三角形全等的条件,并能加以应用.
【自学指导】
活动一
问题1:前面学习的判定方法,直角三角形是否还能用?
2:一个锐角和一条边对应相等的两个直角三角形全等吗 为什么
3:两条直角边对应相等的两个直角三角形全等吗 为什么
4:斜边和一条直角边对应相等的两个直角三角形一定全等吗 为什么
活动二 探究斜边和一条直角边对应相等的两个直角三角形是否全等
阅读教材P13—14探究8,并与同学动手操作作图过程。
思考:从中你发现了什么?(与同学交流你的发现)
【展示知识点】
由活动我们得到:
1.直角三角形的特殊判定定理 的两个直角三角形全等(简称“斜边,直角边”或“HL”)
2.归纳:在什么条件下,两个直角三角形一定全等
①
②
【知识应用】
阅读教材P14例4,完成以下练习
1.如图1,△ABC中,AB=AC,AD是高,则△ADB与△ADC (填“全等”或“不全等” ),根据 (用简写法).
2.判断两个直角三角形全等的条件不正确的是( )
A. 两条直角边对应相等 B. 斜边和一锐角对应相等
C. 斜边和一条直角边对应相等 D. 两个锐角对应相等
3.如图2,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由.
【检测反馈,巩固提高】
如图AB=CD,AE⊥BC,DF⊥BC,CE=BF
求证:(1)AE=DF
(2)CD∥AB
2、△ABC中,AB=AC,M为BC中点,MD⊥AB于D,ME⊥AC于E,求证:MD=ME
【课后反思】
我的问题:
我的小组问题:
课题:11.2三角形全等的判定(第6课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.知道三角形全等的各种判断方法;
2.能根据具体问题合理选择相应的判断方法.
【活动流程】
归纳判断三角形全等的条件
1.填下表:(挂出小黑板,让学生思考、讨论,共同填答).
两个三角形中对应相等的元素 两个三角形是否全等 反例(可画图)
SSS
SAS
SSA
ASA
AAS
AAA
活动二 应用全等判断定理解题
1.如图,AB∥CD,AD∥BC,AC、BD相交于点O.
(1)由AD∥BC,可得 = ,由AB∥CD,
可得 = ,又由 ,于是△ABD≌△CDB;
(2)由△ABD≌△CDB ,可得AD= ,AB= ,
从而还可证明 △AOD≌ ;△AOB≌ .
(3)图中全等三角形共有 对,分别用了哪些判断方法
2.如图,除公共边AB外,根据下列括号内三角形全等的条件,
在横线上添加适当的条件,使△ABC与△ABD全等:
(1) , (SSS);(2) , (ASA);
(3)∠1=∠2 , (SAS);(4) ,∠3=∠4 (AAS).
3.下列各说法中,正确的是( )
A.有两边和一角对应相等的两个三角形全等 B.有两角一边分别相等的两个三角形全等
C.两个锐角对应相等的两个直角三角形全等 D.有两组边相等且周长相等的两个三角形全等
4.如图,已知:AE=CF,AD∥BC,AD=CB. 求证:△ADF≌△ CBE .
5.已知:如图,∠ACB=∠ADB=90°,AC=AD,E在AB上.求证CE=DE.
6.如图,AD与BC相交于O,OC=OD,OA=OB.求证:
7.如图,D,E,F,B在一条直线上,AB=CD,∠B=∠D,BF=DE,
求证:(1)AE=CF ;(2)AE∥CF
课题:11.3角的平分线的性质(第1课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1、会用尺规作图作角平分线;(会说作法)
2、理解并掌握角平分线的性质
3、感受证明一个几何命题的方法与步骤
【自学指导】
活动一 学会作角平分线
自学课本19页(10分钟)
说出探究中AE是∠DAE的平分线的理由
2、 动手操作,作一个角的角平分线
已知:∠AOB.
求作:∠AOB的平分线.
作法:(1)
(2)
(3)
(注意: 角的平分线是一条射线,它不是线段,也不是直线.)
活动二 探究角平分线的性质
阅读课本P20—21,动手操作完成课本第20页的探究。
思考:角平分线上的点到角两边的距离大小关系如何?你能得到什么猜想?把你的猜想写出来。
2.你能证明自己的猜想是正确的吗?试一试。
3.你能结合右图用符号语言表示角平分线的性质吗?
【展示知识点】
⑴ 用尺规怎样画角的平分线_________
⑵角平分线的性质:角的平分线上的点_________
⑶证明几何命题的步骤有_________ _________ _________
【知识应用】
已知∠AOB的角平分线OC,点P在OC上,且点P到OA的距离为4cm,则点P到边OB的距离是__
如图2在△ABC中,∠C=900,AD平分∠BAC,BC=10cm,BD=6cm,
则点D到AB的距离为______
如右图, △ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,
DF⊥AC,垂足分别为E、F. 求证EB=FC .
【检测反馈,巩固提高】
已知△ABC内,∠ABC,∠ACB的角平分线交于点P,且PD、PE、PF分别垂直于BC、AC、AB于D、E、F三点,求证:PD=PE=PF
2.如右图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2.
求:(1)点D到AB的距离;
(2)△ABD的面积.
【课后反思】
我的问题: 我的小组问题:
课题:11.3角的平分线的性质(第2课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.知道角平分线性质定理的逆定理,并会进行应用;
2.注意区别这两个定理的条件和结论,熟练用来解题.
【自学指导】
活动一 复分线的性质定理
1.角平分线性质定理的内容是什么?
如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
(先独立思考解答,然后在组内交流。)
想一想:我们知道: 角平分线上的点到 距离相等;那么到角两边距离相等的点是否也在这个角平分线上呢?
活动二 探究角平分线性质定理的逆命题
1.阅读教材P21 思考,并说明理由。
求证:到角的两边的距离相等的点在角的平分线上(画出图形,写出已知和求证,再加以证明).
【展示知识点】
角平分线性质定理的逆定理:角的内部到角两边距离相等的点_________
【知识应用】角平分线性质定理的逆定理的应用
1.如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,OB=OC.
求证:∠OAB=∠OAC.
【检测反馈,巩固提高】
已知△ABC的外角平分线BD、CE相交于点P . 求证:点P在∠A 的平分线上
2.如图:在△ABC中,∠B=∠C=50°,D是BC的中点,DE⊥AB,DF⊥AC,求∠BAD的度数.
【课后反思】
我的问题:
我的小组问题:
全等三角形复习课 (第1课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.总结三角形全等的识别条件,灵活运用各种判定方法解决问题;
2.培养逻辑思维能力,发展基本的创新意识和能力。
【活动方案】
活动一 填一填,算一算,看谁做得既对又快
1.已知如图(1),≌,其中的对应边:____与____,____与____,____与____,两个全等三角形中对应角有
2.如图(2), ≌,BC的延长线交DA于F,交DE于G, ∠ACB=105 , ∠CAD=10 , ∠D=25 . 求﹦ 、﹦
3.如图(3),在△ABD和△ACE中,有下列论断:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE.请以其中三个论断作为条件,另一个论断作为结论,写出一个真命题:
4. 对于△ABC与△DEF,已知∠A=∠D,∠B=∠E,则下列条件①AB=DE;②AC=DF;③BC=DF;④AB=EF中,能判定它们全等的有( )
A.①② B.①③ C.②③ D.③④
5.下列说法正确的是( )
A.面积相等的两个三角形全等 B.周长相等的两个三角形全等
C.三个角对应相等的两个三角形全等 D.能够完全重合的两个三角形全等
6. 下列数据能确定形状和大小的是( )
A.AB=4,BC=5,∠C=60° B.AB=6,∠C=60°,∠B=70°
C.AB=4,BC=5,CA=10 D.∠C=60°,∠B=70°,∠A=50°
7. 在△ABC和△DEF中,∠A=∠D,AB = DE,添加下列哪一个条件,依然不能证明△ABC≌△DEF( )
A.AC = DF B.BC = EF C.∠B=∠E D.∠C=∠F
思考并交流:在找全等三角形的对应边和对应角时,如何做到对应?
活动二 应用知识,解决问题
如图,在中,,D、E分别为AC、AB上的点,且AD=BD,AE=BC,DE=DC.
求证:DE⊥AB
2.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.求证:AD是△ABC的角平分线.
【检测反馈,巩固提高】
1.如图,图(1)中等腰△ABC与等腰△DEC共点于C,且∠BCA=∠ECD,连结BE,AD,若BC=AC、EC=DC.求证:BE=AD;若将等腰△EDC绕点C旋转至图(2)(3)(4)情况时,其余条件不变,BE与AD还相等吗?为什么
【课后反思】
我的问题: 我的小组问题:
全等三角形复习课(第2课时)
班级: 组名: 姓名: 创作人:_ 使用时间:
【学习目标】
1.会综合运用全等三角形的性质和判定解题;
2.增强观察和理解能力,几何语言的叙述能力及运用全等知识解决实际问题的能力.
【活动方案】
活动一 熟练选用确当的方法证明三角形全等
1.将两根钢条AA/、BB/中点O连在一起,使AA/、BB/绕着点O自由转动,做成一个测量工具,则A/B/的长等于内槽宽AB,判定△OAB≌△OA/B/ 的理由是 .
2.已知AB//DE,且AB=DE,
(1)请你只添加一个条件,使△ABC≌△DEF,你添加的条件是
(2)选其中的一种方法进行证明.
第2题 第3题
3.如图所示,在△ABC和△ABD中,∠C=∠D=90°, 要使△ABC≌△ABD, 还需增加一个条件是__________,请利用你所增加的条件加以证明.
4. 如图,∠1=∠2,∠E=∠A,EC=DA,则△ABD≌△EBC时,运用的判定定理是( )
A.SSS B.ASA C.AAS D.SAS
5. 如图,若线段AB,CD交于点O,且AB、CD互相平分,则下列结论错误的是( )
A.AD=BC B.∠C=∠D C.AD∥BC D.OB=OC
6. 如图,AE⊥BD于E,CF⊥BD于F,AB = CD,AE = CF,
则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
7.如图,DE⊥BC,BE=EC,且AB=5,AC=8,
则△ABD的周长为( )
A.21 B.18 C.13 D.9
8.已知AC//BD,∠CAB和∠DBA的平分线EA、EB与CD相交于点E.
求证:AB=AC+BD.(提示:在AB上截取AF=AC)
【检测反馈,巩固提高】
如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N。
(1)求证:MN=AM+BN。
(2) 若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,
则AM、BN与MN之间有什么关系?请说明理由。
_
D
_
C
_
A
_
B
_
E
A
O
B
A
B
S
D
C
C
B
E
D
A
图4
A
C
D
B
D
A
B
C
A
B
D
C
图1
图2
A
B
C
3
4
1
2.如图,除公共边AB外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使△ABC与△ABD全等:
(1) , (SSS);(2) , (ASA);
(3)∠1=∠2 , (SAS);(4) ,∠3=∠4 (AAS).
2
D
A
E
C
D
B
C
D
E
F
A
B
B
C
(图3)
A
D
E
图1
图2
图(2)
B
E
C
A
F
D
(1)
(2)
(3)
(4)
B
C
A
D
B
A
C
E
D
(第4题)
2
1
O
A
D
C
B
(第5题)
(第6题)
A
D
C
B
E
F
E
B
A
D
C
(第7题)
