贵州省兴义七中2013届高三上学期8月月考文科数学试题
文档属性
| 名称 | 贵州省兴义七中2013届高三上学期8月月考文科数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 95.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-16 00:00:00 | ||
图片预览


文档简介
贵州省兴义七中2013届高三上学期8月月考文科数学试题
I 卷
一、选择题
1. 下列判断正确的是( )
A.函数是奇函数; B.函数是偶函数
C.函数是非奇非偶函数 D.函数既是奇函数又是偶函数
【答案】C
2.为了得到函数的图象,只需把函数的图象 ( )
A.向上平移一个单位 B.向下平移一个单位
C.向左平移一个单位 D.向右平移一个单位
【答案】D
3.函数的定义域为( )
A. B. C. D.
【答案】C
4.函数y = f(|x|)的图象如右图所示,则函数y = f(x)的图象不可能是 ( )
【答案】B
5.对于函数,以下说法正确的有 ( )
①是的函数;②对于不同的的值也不同;③表示当时函数的值,是一个常量;④一定可以用一个具体的式子表示出来。
A.1个 B.2个 C.3个 D.4个
【答案】B
6.在同一个坐标系中画出函数的部分图象,其中,则下列所给图象中可能正确的是( )
【答案】D
7.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )
A.y=x3 B.y=|x|+1
C.y=-x2+1 D.y=2-|x|
【答案】B
8.已知函数是奇函数,当时,则的值等于( )
A. C. D.-
【答案】D
9.函数的值域为 ( )
A. B. C. D.
【答案】A
10.下列函数中,与函数y=有相同定义域的是( )
A.f(x)=log2x B.f(x)=
C.f(x)=|x| D.f(x)=2x
【答案】A
11. 指数函数y=ax的图像经过点(2,16)则a的值是 ( )
A. B. C.2 D.4
【答案】D
12. 设为偶函数,对于任意的的数都有,已知,那么等于 ( )
A.2 B.-2 C..8 D.-8
【答案】C
II卷
二、填空题
13.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)=________.
【答案】-3
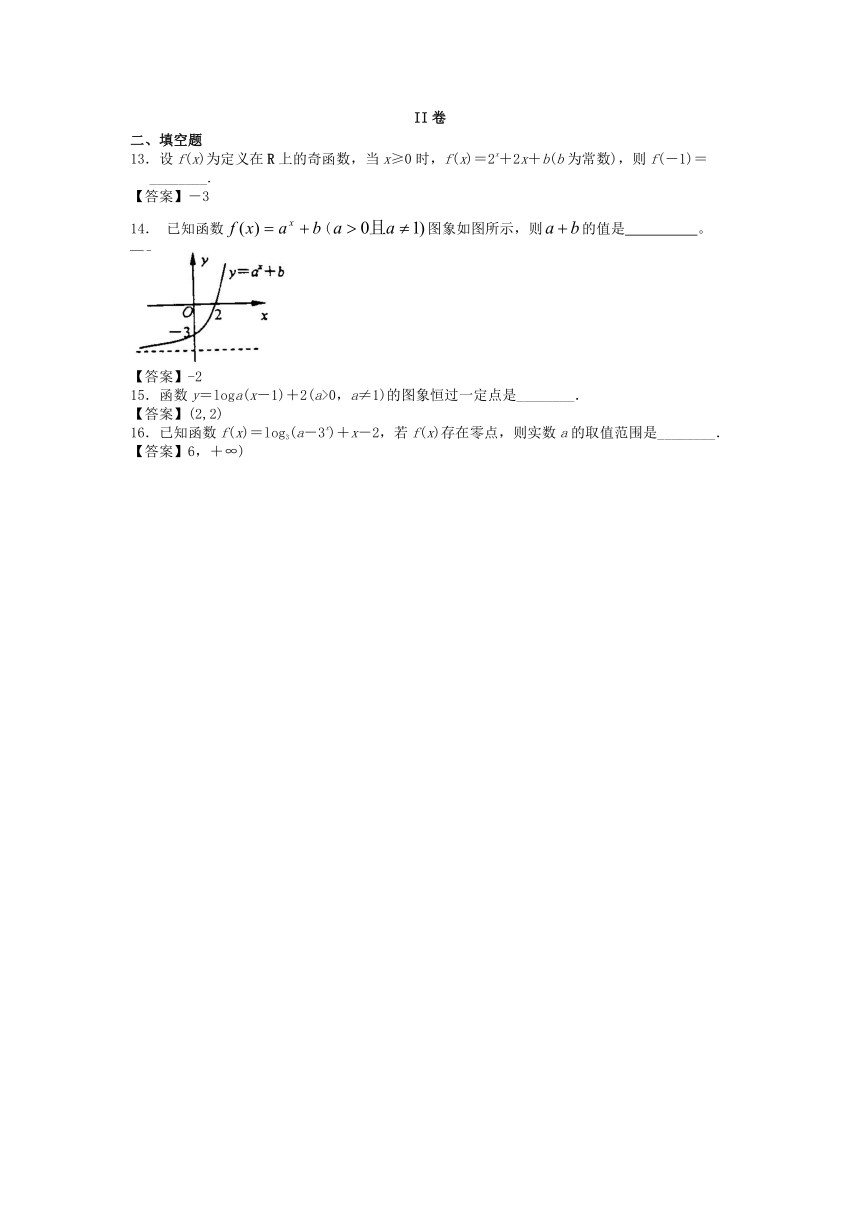
14. 已知函数(图象如图所示,则的值是 。
【答案】-2
15.函数y=loga(x-1)+2(a>0,a≠1)的图象恒过一定点是________.
【答案】(2,2)
16.已知函数f(x)=log3(a-3x)+x-2,若f(x)存在零点,则实数a的取值范围是________.
【答案】6,+∞)
三、解答题
17.若函数y=f(x)是周期为2的偶函数,当x∈[2,3]时,f(x)=x-1.在y=f(x)的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,a)(其中2(1) 求当x∈[1,2]时,f(x)的解析式;
(2) 定点C的坐标为(0,a)(其中2【答案】(1)∵f(x)是以2为周期的周期函数,当x∈[2,3]时,f(x)=x-1,
∴当x∈[0,1]时,f(x)=f(x+2)=(x+2)-1=x+1.
∵f(x)是偶函数,∴当x∈[-1,0]时,f(x)=f(-x)=-x+1,
当x∈[1,2]时,f(x)=f(x-2)=-(x-2)+1=-x+3.
(2)设A、B的横坐标分别为3-t,t+1,1≤t≤2,则|AB|=(t+1)-(3-t)=2t-2,
∴△ABC的面积为S=(2t-2)·(a-t)=-t2+(a+1)t-a(1≤t≤2)=-(t-)2+
∵218.已知定义在实数集上的奇函数有最小正周期2,且当时,
(Ⅰ)求函数在上的解析式; (Ⅱ)判断在上的单调性;
(Ⅲ)当取何值时,方程在上有实数解?
【答案】(Ⅰ)∵f(x)是x∈R上的奇函数,∴f(0)=0.
设x∈(-1,0), 则-x∈(0,1),
(Ⅱ)设,
∵,∴,
∴
∴f(x)在(0,1)上为减函数.
(Ⅲ)∵f(x)在(0,1)上为减函数,
∴
方程上有实数解.
19.设函数(a为实数).⑴若a<0,用函数单调性定义证明:在上是增函数;⑵若a=0,的图象与的图象关于直线y=x对称,求函数的解析式.
【答案】 (1)设任意实数x1==
.
又,∴f(x1)- f(x2)<0,所以f(x)是增函数.
(2)当a=0时,y=f(x)=2x-1,∴2x=y+1, ∴x=log2(y+1),
y=g(x)= log2(x+1).
解析:通过用定义证明函数的单调性考查指数函数的运算及其性质,通过求关于直线y=x对称函数的解析式考查指对互化及简单求反函数的方法,该题属于简单题.
20.如果函数f(x)的定义域为{x|x>0},且f(x)为增函数,f(x·y)=f(x)+f(y).
(1)求证:f()=f(x)-f(y);
(2)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围.
【答案】(1)证明:∵f(x)=f(·y)=f()+f(y),
∴f()=f(x)-f(y).
(2)∵f(3)=1,f(a)>f(a-1)+2,
∴f(a)-f(a-1)>2.
∴f()>2=f(3)+f(3)=f(9).
∵f(x)是增函数,
∴>9.又a>0,a-1>0,∴1∴a的取值范围是121.已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)若方程f(x)-m=0有解,求m的取值范围.
【答案】(1)由函数f(x)是偶函数,可知f(x)=f(-x).
∴log4(4x+1)+kx=log4(4-x+1)-kx.
即log4=-2kx,
log44x=-2kx,
∴x=-2kx对一切x∈R恒成立.∴k=-.
(2)由m=f(x)=log4(4x+1)-x,
∴m=log4=log4(2x+).
∵2x+≥2,∴m≥.
故要使方程f(x)-m=0有解,m的取值范围为m≥.
22.提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度(单位:千米小时)是车流密度(单位:辆千米)的函数,当桥上的的车流密度达到200辆千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆千米时,车流速度为60千米小时,研究表明;当时,车流速度是车流密度的一次函数.
(Ⅰ)当时,求函数的表达式;
(Ⅱ)当车流密度为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆每小时)可以达到最大,并求最大值(精确到1辆小时).
【答案】(1)由题意,当时,;当时,设
由已知,解得.
故函数的表达式为.
(2)由题意并由(1)可得
当时,为增函数,故当时,其最大值为;
当时,
当且仅当即时等号成立.
所以当时,在区间上取得最大值.
综上可知,当时, 在区间上取得最大值.
即当车流密度为100辆千米时,车流量可以达到最大,最大值约为3333辆小时
I 卷
一、选择题
1. 下列判断正确的是( )
A.函数是奇函数; B.函数是偶函数
C.函数是非奇非偶函数 D.函数既是奇函数又是偶函数
【答案】C
2.为了得到函数的图象,只需把函数的图象 ( )
A.向上平移一个单位 B.向下平移一个单位
C.向左平移一个单位 D.向右平移一个单位
【答案】D
3.函数的定义域为( )
A. B. C. D.
【答案】C
4.函数y = f(|x|)的图象如右图所示,则函数y = f(x)的图象不可能是 ( )
【答案】B
5.对于函数,以下说法正确的有 ( )
①是的函数;②对于不同的的值也不同;③表示当时函数的值,是一个常量;④一定可以用一个具体的式子表示出来。
A.1个 B.2个 C.3个 D.4个
【答案】B
6.在同一个坐标系中画出函数的部分图象,其中,则下列所给图象中可能正确的是( )
【答案】D
7.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )
A.y=x3 B.y=|x|+1
C.y=-x2+1 D.y=2-|x|
【答案】B
8.已知函数是奇函数,当时,则的值等于( )
A. C. D.-
【答案】D
9.函数的值域为 ( )
A. B. C. D.
【答案】A
10.下列函数中,与函数y=有相同定义域的是( )
A.f(x)=log2x B.f(x)=
C.f(x)=|x| D.f(x)=2x
【答案】A
11. 指数函数y=ax的图像经过点(2,16)则a的值是 ( )
A. B. C.2 D.4
【答案】D
12. 设为偶函数,对于任意的的数都有,已知,那么等于 ( )
A.2 B.-2 C..8 D.-8
【答案】C
II卷
二、填空题
13.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)=________.
【答案】-3
14. 已知函数(图象如图所示,则的值是 。
【答案】-2
15.函数y=loga(x-1)+2(a>0,a≠1)的图象恒过一定点是________.
【答案】(2,2)
16.已知函数f(x)=log3(a-3x)+x-2,若f(x)存在零点,则实数a的取值范围是________.
【答案】6,+∞)
三、解答题
17.若函数y=f(x)是周期为2的偶函数,当x∈[2,3]时,f(x)=x-1.在y=f(x)的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,a)(其中2
(2) 定点C的坐标为(0,a)(其中2
∴当x∈[0,1]时,f(x)=f(x+2)=(x+2)-1=x+1.
∵f(x)是偶函数,∴当x∈[-1,0]时,f(x)=f(-x)=-x+1,
当x∈[1,2]时,f(x)=f(x-2)=-(x-2)+1=-x+3.
(2)设A、B的横坐标分别为3-t,t+1,1≤t≤2,则|AB|=(t+1)-(3-t)=2t-2,
∴△ABC的面积为S=(2t-2)·(a-t)=-t2+(a+1)t-a(1≤t≤2)=-(t-)2+
∵2
(Ⅰ)求函数在上的解析式; (Ⅱ)判断在上的单调性;
(Ⅲ)当取何值时,方程在上有实数解?
【答案】(Ⅰ)∵f(x)是x∈R上的奇函数,∴f(0)=0.
设x∈(-1,0), 则-x∈(0,1),
(Ⅱ)设,
∵,∴,
∴
∴f(x)在(0,1)上为减函数.
(Ⅲ)∵f(x)在(0,1)上为减函数,
∴
方程上有实数解.
19.设函数(a为实数).⑴若a<0,用函数单调性定义证明:在上是增函数;⑵若a=0,的图象与的图象关于直线y=x对称,求函数的解析式.
【答案】 (1)设任意实数x1
.
又,∴f(x1)- f(x2)<0,所以f(x)是增函数.
(2)当a=0时,y=f(x)=2x-1,∴2x=y+1, ∴x=log2(y+1),
y=g(x)= log2(x+1).
解析:通过用定义证明函数的单调性考查指数函数的运算及其性质,通过求关于直线y=x对称函数的解析式考查指对互化及简单求反函数的方法,该题属于简单题.
20.如果函数f(x)的定义域为{x|x>0},且f(x)为增函数,f(x·y)=f(x)+f(y).
(1)求证:f()=f(x)-f(y);
(2)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围.
【答案】(1)证明:∵f(x)=f(·y)=f()+f(y),
∴f()=f(x)-f(y).
(2)∵f(3)=1,f(a)>f(a-1)+2,
∴f(a)-f(a-1)>2.
∴f()>2=f(3)+f(3)=f(9).
∵f(x)是增函数,
∴>9.又a>0,a-1>0,∴1
(1)求k的值;
(2)若方程f(x)-m=0有解,求m的取值范围.
【答案】(1)由函数f(x)是偶函数,可知f(x)=f(-x).
∴log4(4x+1)+kx=log4(4-x+1)-kx.
即log4=-2kx,
log44x=-2kx,
∴x=-2kx对一切x∈R恒成立.∴k=-.
(2)由m=f(x)=log4(4x+1)-x,
∴m=log4=log4(2x+).
∵2x+≥2,∴m≥.
故要使方程f(x)-m=0有解,m的取值范围为m≥.
22.提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度(单位:千米小时)是车流密度(单位:辆千米)的函数,当桥上的的车流密度达到200辆千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆千米时,车流速度为60千米小时,研究表明;当时,车流速度是车流密度的一次函数.
(Ⅰ)当时,求函数的表达式;
(Ⅱ)当车流密度为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆每小时)可以达到最大,并求最大值(精确到1辆小时).
【答案】(1)由题意,当时,;当时,设
由已知,解得.
故函数的表达式为.
(2)由题意并由(1)可得
当时,为增函数,故当时,其最大值为;
当时,
当且仅当即时等号成立.
所以当时,在区间上取得最大值.
综上可知,当时, 在区间上取得最大值.
即当车流密度为100辆千米时,车流量可以达到最大,最大值约为3333辆小时
同课章节目录
