贵州省兴义四中2013届高三上学期8月月考文科数学试题
文档属性
| 名称 | 贵州省兴义四中2013届高三上学期8月月考文科数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 132.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-16 07:55:45 | ||
图片预览


文档简介
贵州省兴义四中2013届高三上学期8月月考文科数学试题
I 卷
一、选择题
1. 下列判断正确的是( )
A.函数是奇函数; B.函数是偶函数
C.函数是非奇非偶函数 D.函数既是奇函数又是偶函数
【答案】C
2.为了得到函数的图象,只需把函数的图象 ( )
A.向上平移一个单位 B.向下平移一个单位
C.向左平移一个单位 D.向右平移一个单位
【答案】D
3.已知函数的定义域为R,,对任意都有( )
A. B. C. D.
【答案】B
解析:由
所以
所以.
4.函数(x≤0)的反函数是 ( )
A. B.
C. D.
【答案】D
5. ( )
A. B. C. D.
【答案】C
6.偶函数f(x)满足f (x-1)= f (x+1),且在x0,1时,f (x)=1-x,则关于x的方程f (x)=()x,在x0,3上解的个数是( )
A.1 B.2 C.3 D.4
【答案】D
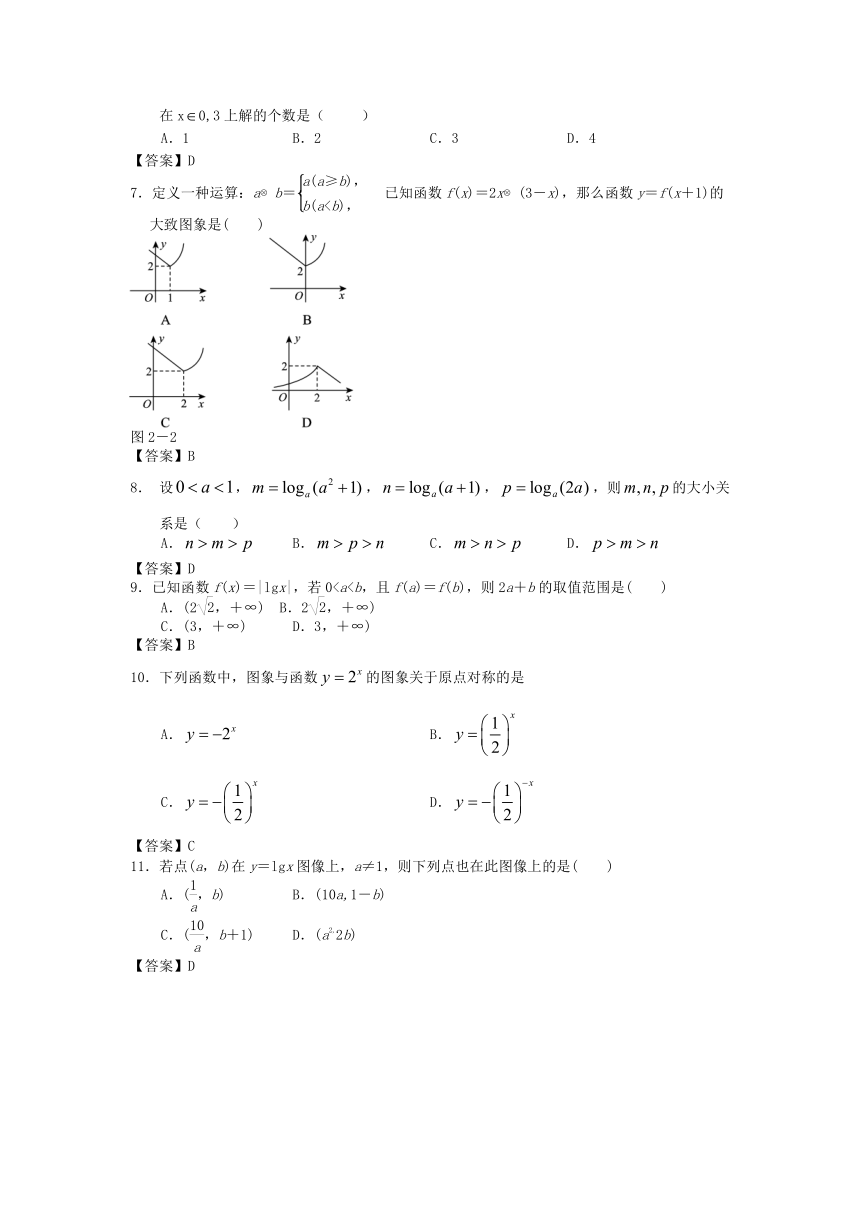
7.定义一种运算:a b=已知函数f(x)=2x (3-x),那么函数y=f(x+1)的大致图象是( )
图2-2
【答案】B
8. 设,,,,则的大小关系是( )
A. B. C. D.
【答案】D
9.已知函数f(x)=|lgx|,若0A.(2,+∞) B.2,+∞)
C.(3,+∞) D.3,+∞)
【答案】B
10.下列函数中,图象与函数的图象关于原点对称的是 ( )
A. B.
C. D.
【答案】C
11.若点(a,b)在y=lgx图像上,a≠1,则下列点也在此图像上的是( )
A.(,b) B.(10a,1-b)
C.(,b+1) D.(a2,2b)
【答案】D
II卷
二、填空题
12.已知函数f(x)=若f(2-a2)>f(a),则实数a的取值范围是________.
【答案】(-2,1)
13.下列函数f(x)中,满足“对任意x1,x2∈(0,+∞),当x1①f(x)=;
②f(x)=(x-1)2;
③f(x)=ex;
④f(x)=1n(x+1).
【答案】③④
14.函数y=()x-log2(x+2)在-1,1上的最大值为________.
【答案】3
15.函数y=()x-log2(x+2)在-1,1上的最大值为________.
【答案】3
三、解答题
16.若函数y=f(x)是周期为2的偶函数,当x∈[2,3]时,f(x)=x-1.在y=f(x)的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,a)(其中2(1) 求当x∈[1,2]时,f(x)的解析式;
(2) 定点C的坐标为(0,a)(其中2【答案】(1)∵f(x)是以2为周期的周期函数,当x∈[2,3]时,f(x)=x-1,
∴当x∈[0,1]时,f(x)=f(x+2)=(x+2)-1=x+1.
∵f(x)是偶函数,∴当x∈[-1,0]时,f(x)=f(-x)=-x+1,
当x∈[1,2]时,f(x)=f(x-2)=-(x-2)+1=-x+3.
(2)设A、B的横坐标分别为3-t,t+1,1≤t≤2,则|AB|=(t+1)-(3-t)=2t-2,
∴△ABC的面积为S=(2t-2)·(a-t)=-t2+(a+1)t-a(1≤t≤2)=-(t-)2+
∵217.已知函数,
(1)判断函数的奇偶性;
(2)求证:在上为增函数;
【答案】(1)函数的定义域为R,且,
所以
.
即,所以是奇函数.
(2),有,
,,,,.
所以,函数在R上是增函数.
18.某公司计划投资、两种金融产品,根据市场调查与预测,A产品的利润与投资量成正比例,其关系如图1,B产品的利润与投资量的算术平方要成正比例,其关系如图2.(注:利润与投资量的单位:万元)
(1)分别将、两产品的利润表示为投资量的函数关系式;
(2)该公司已有10万元资金,并全部投入、两种产品中,问:怎样分配这10万元投资,才能使公司获得最大利润?其最大利润为多少万元?
【答案】(1)设投资万元,A产品的利润为万元,B产品的利润为万元,
依题意可设.
由图1,得即.
由图2,得即
故.
(2)设B产品投入万元,则A产品投入10-万元,设企业利润为万元,
由(1)得
,
当,即时,.
因此当A产品投入6万元,B产品投入4万元时,该企业获得最大利润为2.8万元。
19.某市出租车的计价标准是:3 km以内(含3 km)10元;超出3 km但不超过18 km的部分1元km;超出18 km的部分2元km.
(1)如果某人乘车行驶了20 km,他要付多少车费?某人乘车行驶了x km,他要付多少车费?
(2)如果某人付了22元的车费,他乘车坐了多远?某人付了10+x(x>0)元的车费,他乘车坐了多远?
【答案】(1)乘车行驶了20 km,付费分三部分,前3 km付费10(元),3 km到18 km付费(18-3)×1=15(元),18 km到20 km付费(20-18)×2=4(元),
故总付费10+15+4=29(元).
设付车费y元,当0当3当x>18时,车费y=25+2(x-18)=2x-11.
故y=
(2)付出22元的车费,说明此人乘车行驶的路程大于3 km,且小于18 km.前3 km付费10元,余下的12元乘车行驶了12 km,故此人乘车行驶了15 km.
设乘车行驶了y km,当0当x>15时,y=18+=x+.
故y=
20.已知函数f(x)=a·2x+b·3x,其中常数a,b满足ab≠0.
(1)若ab>0,判断函数f(x)的单调性;
(2)若ab<0,求f(x+1)>f(x)时x的取值范围.
【答案】(1)当a>0,b>0时,任意x1,x2∈R,x1则f(x1)-f(x2)=a(2x1-2x2)+b(3x1-3x2).
∵2x1<2x2,a>0 a(2x1-2x2)<0,
3x1<3x2,b>0 b(3x1-3x2)<0,
∴f(x1)-f(x2)<0,函数f(x)在R上是增函数.
当a<0,b<0时,同理,函数f(x)在R上是减函数.
(2)f(x+1)-f(x)=a·2x+2b·3x>0,
当a<0,b>0时,>-,
则x>;
当a>0,b<0时, <-,
则x21.已知是奇函数,且,
(1)求实数p和q;
(2)求f(x)的单调区间.
【答案】(1)是奇函数,
即
又
(2)
,令即为增区间
令即为减区间.
I 卷
一、选择题
1. 下列判断正确的是( )
A.函数是奇函数; B.函数是偶函数
C.函数是非奇非偶函数 D.函数既是奇函数又是偶函数
【答案】C
2.为了得到函数的图象,只需把函数的图象 ( )
A.向上平移一个单位 B.向下平移一个单位
C.向左平移一个单位 D.向右平移一个单位
【答案】D
3.已知函数的定义域为R,,对任意都有( )
A. B. C. D.
【答案】B
解析:由
所以
所以.
4.函数(x≤0)的反函数是 ( )
A. B.
C. D.
【答案】D
5. ( )
A. B. C. D.
【答案】C
6.偶函数f(x)满足f (x-1)= f (x+1),且在x0,1时,f (x)=1-x,则关于x的方程f (x)=()x,在x0,3上解的个数是( )
A.1 B.2 C.3 D.4
【答案】D
7.定义一种运算:a b=已知函数f(x)=2x (3-x),那么函数y=f(x+1)的大致图象是( )
图2-2
【答案】B
8. 设,,,,则的大小关系是( )
A. B. C. D.
【答案】D
9.已知函数f(x)=|lgx|,若0
C.(3,+∞) D.3,+∞)
【答案】B
10.下列函数中,图象与函数的图象关于原点对称的是 ( )
A. B.
C. D.
【答案】C
11.若点(a,b)在y=lgx图像上,a≠1,则下列点也在此图像上的是( )
A.(,b) B.(10a,1-b)
C.(,b+1) D.(a2,2b)
【答案】D
II卷
二、填空题
12.已知函数f(x)=若f(2-a2)>f(a),则实数a的取值范围是________.
【答案】(-2,1)
13.下列函数f(x)中,满足“对任意x1,x2∈(0,+∞),当x1
②f(x)=(x-1)2;
③f(x)=ex;
④f(x)=1n(x+1).
【答案】③④
14.函数y=()x-log2(x+2)在-1,1上的最大值为________.
【答案】3
15.函数y=()x-log2(x+2)在-1,1上的最大值为________.
【答案】3
三、解答题
16.若函数y=f(x)是周期为2的偶函数,当x∈[2,3]时,f(x)=x-1.在y=f(x)的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,a)(其中2
(2) 定点C的坐标为(0,a)(其中2
∴当x∈[0,1]时,f(x)=f(x+2)=(x+2)-1=x+1.
∵f(x)是偶函数,∴当x∈[-1,0]时,f(x)=f(-x)=-x+1,
当x∈[1,2]时,f(x)=f(x-2)=-(x-2)+1=-x+3.
(2)设A、B的横坐标分别为3-t,t+1,1≤t≤2,则|AB|=(t+1)-(3-t)=2t-2,
∴△ABC的面积为S=(2t-2)·(a-t)=-t2+(a+1)t-a(1≤t≤2)=-(t-)2+
∵2
(1)判断函数的奇偶性;
(2)求证:在上为增函数;
【答案】(1)函数的定义域为R,且,
所以
.
即,所以是奇函数.
(2),有,
,,,,.
所以,函数在R上是增函数.
18.某公司计划投资、两种金融产品,根据市场调查与预测,A产品的利润与投资量成正比例,其关系如图1,B产品的利润与投资量的算术平方要成正比例,其关系如图2.(注:利润与投资量的单位:万元)
(1)分别将、两产品的利润表示为投资量的函数关系式;
(2)该公司已有10万元资金,并全部投入、两种产品中,问:怎样分配这10万元投资,才能使公司获得最大利润?其最大利润为多少万元?
【答案】(1)设投资万元,A产品的利润为万元,B产品的利润为万元,
依题意可设.
由图1,得即.
由图2,得即
故.
(2)设B产品投入万元,则A产品投入10-万元,设企业利润为万元,
由(1)得
,
当,即时,.
因此当A产品投入6万元,B产品投入4万元时,该企业获得最大利润为2.8万元。
19.某市出租车的计价标准是:3 km以内(含3 km)10元;超出3 km但不超过18 km的部分1元km;超出18 km的部分2元km.
(1)如果某人乘车行驶了20 km,他要付多少车费?某人乘车行驶了x km,他要付多少车费?
(2)如果某人付了22元的车费,他乘车坐了多远?某人付了10+x(x>0)元的车费,他乘车坐了多远?
【答案】(1)乘车行驶了20 km,付费分三部分,前3 km付费10(元),3 km到18 km付费(18-3)×1=15(元),18 km到20 km付费(20-18)×2=4(元),
故总付费10+15+4=29(元).
设付车费y元,当0
故y=
(2)付出22元的车费,说明此人乘车行驶的路程大于3 km,且小于18 km.前3 km付费10元,余下的12元乘车行驶了12 km,故此人乘车行驶了15 km.
设乘车行驶了y km,当0
故y=
20.已知函数f(x)=a·2x+b·3x,其中常数a,b满足ab≠0.
(1)若ab>0,判断函数f(x)的单调性;
(2)若ab<0,求f(x+1)>f(x)时x的取值范围.
【答案】(1)当a>0,b>0时,任意x1,x2∈R,x1
∵2x1<2x2,a>0 a(2x1-2x2)<0,
3x1<3x2,b>0 b(3x1-3x2)<0,
∴f(x1)-f(x2)<0,函数f(x)在R上是增函数.
当a<0,b<0时,同理,函数f(x)在R上是减函数.
(2)f(x+1)-f(x)=a·2x+2b·3x>0,
当a<0,b>0时,>-,
则x>;
当a>0,b<0时, <-,
则x
(1)求实数p和q;
(2)求f(x)的单调区间.
【答案】(1)是奇函数,
即
又
(2)
,令即为增区间
令即为减区间.
同课章节目录
