贵州省普安二中2013届高三上学期8月月考文科数学试题
文档属性
| 名称 | 贵州省普安二中2013届高三上学期8月月考文科数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 103.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-16 07:57:36 | ||
图片预览



文档简介
贵州省普安二中2013届高三上学期8月月考文科数学试题
I 卷
一、选择题
1.若与在区间1,2上都是减函数,则的取值范围是( )
A. (0,1) B. (0,1
C. (-1,0)∪(0,1) D. (-1,0) ∪(0,1
【答案】B
2. 下列判断正确的是( )
A.函数是奇函数; B.函数是偶函数
C.函数是非奇非偶函数 D.函数既是奇函数又是偶函数
【答案】C
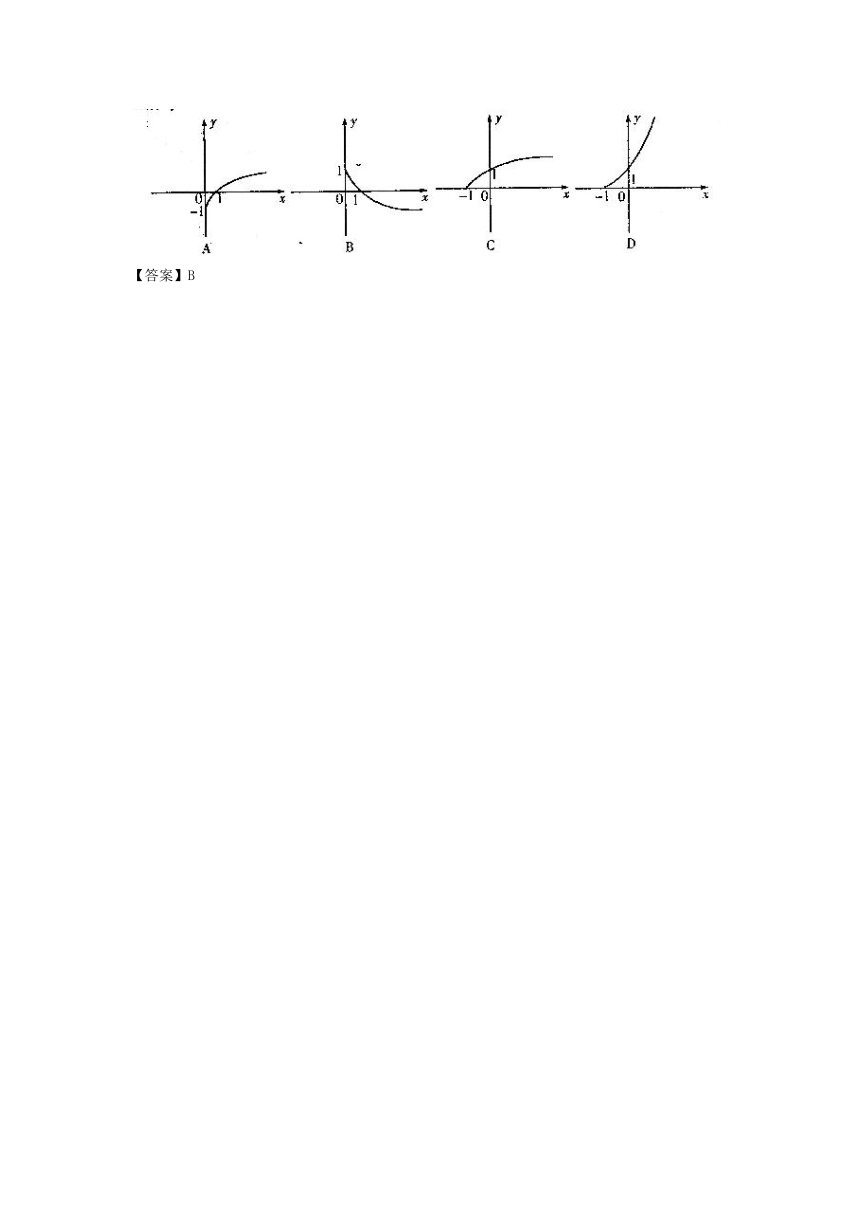
3.如图1,当参数时,连续函数 的图像分别对应曲线和 , 则( )
A B
C D
【答案】B
4.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )
A.y=x3 B.y=|x|+1
C.y=-x2+1 D.y=2-|x|
【答案】B
5. 已知且 的值( )
A.一定小于0 B.等于0 C.一定大于0 D.无法确定
【答案】A
6.已知函数f(x)=|lgx|,若0A.(2,+∞) B.2,+∞)
C.(3,+∞) D.3,+∞)
【答案】B
7.已知函数是偶函数,上是单调减函数,则( )
A. B.
C. D.
【答案】A
8. 设为偶函数,对于任意的的数都有,已知,那么等于 ( )
A.2 B.-2 C..8 D.-8
【答案】C
9. 函数的定义域是 ( )
A. B. C. D.
【答案】B
10.已知是函数的一个零点,若,则
A. B.
C. D.
【答案】D
11.在函数的图象上有一点,此函数图象与轴、直线围成图形(如图阴影部分)的面积为S,则S与的函数关系图象可表示为 ( )
【答案】B
12.函数的图象关于x轴对称的图象大致是( )
【答案】B
II卷
二、填空题
13.设,定义P※Q=,则P※Q中元素的个数为 .
【答案】12
14.若函数在区间上的最大值为4,则的值为_________.
【答案】1或–1
15.已知函数,若,则的取值范围为 。
【答案】
16.若则5 .
【答案】
三、解答题
17.已知函数定义域为,若对于任意的,,都有,且>0时,有>0.
⑴证明: 为奇函数;
⑵证明: 在上为单调递增函数;
⑶设=1,若<,对所有恒成立,求实数的取值范围.
【答案】(1)令,
令,,为奇函数
(2)
在上为单调递增函数;
(3)在上为单调递增函数,,使对所有恒成立,只要>1,即>0
令
18.如果函数f(x)的定义域为{x|x>0},且f(x)为增函数,f(x·y)=f(x)+f(y).
(1)求证:f()=f(x)-f(y);
(2)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围.
【答案】(1)证明:∵f(x)=f(·y)=f()+f(y),
∴f()=f(x)-f(y).
(2)∵f(3)=1,f(a)>f(a-1)+2,
∴f(a)-f(a-1)>2.
∴f()>2=f(3)+f(3)=f(9).
∵f(x)是增函数,
∴>9.又a>0,a-1>0,∴1∴a的取值范围是119.已知函数f(x)=x3-x2+ax-a(a∈R).
(1)当a=-3时,求函数f(x)的极值;
(2)求证:当a≥1时,函数f(x)的图象与x轴有且只有一个交点.
【答案】(1) 当a=-3时,f(x)=x3-x2-3x+3,
∴f′(x)=x2-2x-3=(x-3)(x+1).
令f′(x)=0,得x1=-1,x2=3.
当x<-1时,f′(x)>0,则f(x)在(-∞,-1)上单调递增;
当-1当x>3时,f′(x)>0,f(x)在(3,+∞)上单调递增.
∴当x=-1时,f(x)取得极大值为
f(-1)=--1+3+3=;
当x=3时,f(x)取得极小值为
f(3)=×27-9-9+3=-6.
(2) ∵f′(x)=x2-2x+a,
∴Δ=4-4a=4(1-a).
由a≥1,则Δ≤0,∴f′(x)≥0在R上恒成立,
∴f(x)在R上单调递增.
∵f(0)=-a<0,f(3)=2a>0,
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点.
20.已知函数
(1)若在区间[1,+)上是增函数,求实数的取值范围
(2)若是的极值点,求在[1,]上的最大值
(3)在(2)的条件下,是否存在实数b,使得函数的图象与的图象恰有3个交点?若存在,请求出实数b的取值范围;若不存在,试说明理由.
【答案】(1)
在是增函数,
在上恒有,即
在[1,+)上恒成立,
则必有且
(2)依题意,
即
令,
得.
则当经变化时,与变化情况如下表
1 (1,3) 3 (3,4) 4
- 0 +
-6 -18 -12
在[1,4]上的最大值是.
C.函数的图象与函数的图象恰有3个交点,即方程恰有3个不等实根.
有两个非零不等实根.
是其中一个根,
且.
存在满足条件的b的值,b的取值范围是且.
21.某企业去年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+)万元(n为正整数).
(Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为万元,进行技术改造后的累计纯利润为万元(须扣除技术改造资金),求、的表达式;
(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
【答案】(Ⅰ)依题意知,数列是一个以500为首项,-20为公差的等差数列,所以,
=
=
=
(Ⅱ)依题意得,,即,
可化简得,
可设,
又,可设是减函数,是增函数,
又
则时不等式成立,即4年
22.已知函数f(x)=loga(1+x),g(x)=loga(1-x),其中(a>0且a≠1),设h(x)=f(x)-g(x).
(1)求函数h(x)的定义域;
(2)判断h(x)的奇偶性,并说明理由;
(3)若f(3)=2,求使h(x)>0成立的x的集合.
【答案】(1)由对数的意义,分别得1+x>0,1-x>0,即x>-1,x<1.∴函数f(x)的定义域为(-1,+∞),函数g(x)的定义域为(-∞,1),
∴函数h(x)的定义域为(-1,1).
(2)∵对任意的x∈(-1,1),-x∈(-1,1),
h(-x)=f(-x)-g(-x)
=loga(1-x)-loga(1+x)
=g(x)-f(x)=-h(x),
∴h(x)是奇函数.
(3)由f(3)=2,得a=2.
此时h(x)=log2(1+x)-log2(1-x),
由h(x)>0即log2(1+x)-log2(1-x)>0,
∴log2(1+x)>log2(1-x).
由1+x>1-x>0,解得0故使h(x)>0成立的x的集合是{x|0
I 卷
一、选择题
1.若与在区间1,2上都是减函数,则的取值范围是( )
A. (0,1) B. (0,1
C. (-1,0)∪(0,1) D. (-1,0) ∪(0,1
【答案】B
2. 下列判断正确的是( )
A.函数是奇函数; B.函数是偶函数
C.函数是非奇非偶函数 D.函数既是奇函数又是偶函数
【答案】C
3.如图1,当参数时,连续函数 的图像分别对应曲线和 , 则( )
A B
C D
【答案】B
4.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )
A.y=x3 B.y=|x|+1
C.y=-x2+1 D.y=2-|x|
【答案】B
5. 已知且 的值( )
A.一定小于0 B.等于0 C.一定大于0 D.无法确定
【答案】A
6.已知函数f(x)=|lgx|,若0
C.(3,+∞) D.3,+∞)
【答案】B
7.已知函数是偶函数,上是单调减函数,则( )
A. B.
C. D.
【答案】A
8. 设为偶函数,对于任意的的数都有,已知,那么等于 ( )
A.2 B.-2 C..8 D.-8
【答案】C
9. 函数的定义域是 ( )
A. B. C. D.
【答案】B
10.已知是函数的一个零点,若,则
A. B.
C. D.
【答案】D
11.在函数的图象上有一点,此函数图象与轴、直线围成图形(如图阴影部分)的面积为S,则S与的函数关系图象可表示为 ( )
【答案】B
12.函数的图象关于x轴对称的图象大致是( )
【答案】B
II卷
二、填空题
13.设,定义P※Q=,则P※Q中元素的个数为 .
【答案】12
14.若函数在区间上的最大值为4,则的值为_________.
【答案】1或–1
15.已知函数,若,则的取值范围为 。
【答案】
16.若则5 .
【答案】
三、解答题
17.已知函数定义域为,若对于任意的,,都有,且>0时,有>0.
⑴证明: 为奇函数;
⑵证明: 在上为单调递增函数;
⑶设=1,若<,对所有恒成立,求实数的取值范围.
【答案】(1)令,
令,,为奇函数
(2)
在上为单调递增函数;
(3)在上为单调递增函数,,使对所有恒成立,只要>1,即>0
令
18.如果函数f(x)的定义域为{x|x>0},且f(x)为增函数,f(x·y)=f(x)+f(y).
(1)求证:f()=f(x)-f(y);
(2)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围.
【答案】(1)证明:∵f(x)=f(·y)=f()+f(y),
∴f()=f(x)-f(y).
(2)∵f(3)=1,f(a)>f(a-1)+2,
∴f(a)-f(a-1)>2.
∴f()>2=f(3)+f(3)=f(9).
∵f(x)是增函数,
∴>9.又a>0,a-1>0,∴1
(1)当a=-3时,求函数f(x)的极值;
(2)求证:当a≥1时,函数f(x)的图象与x轴有且只有一个交点.
【答案】(1) 当a=-3时,f(x)=x3-x2-3x+3,
∴f′(x)=x2-2x-3=(x-3)(x+1).
令f′(x)=0,得x1=-1,x2=3.
当x<-1时,f′(x)>0,则f(x)在(-∞,-1)上单调递增;
当-1
∴当x=-1时,f(x)取得极大值为
f(-1)=--1+3+3=;
当x=3时,f(x)取得极小值为
f(3)=×27-9-9+3=-6.
(2) ∵f′(x)=x2-2x+a,
∴Δ=4-4a=4(1-a).
由a≥1,则Δ≤0,∴f′(x)≥0在R上恒成立,
∴f(x)在R上单调递增.
∵f(0)=-a<0,f(3)=2a>0,
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点.
20.已知函数
(1)若在区间[1,+)上是增函数,求实数的取值范围
(2)若是的极值点,求在[1,]上的最大值
(3)在(2)的条件下,是否存在实数b,使得函数的图象与的图象恰有3个交点?若存在,请求出实数b的取值范围;若不存在,试说明理由.
【答案】(1)
在是增函数,
在上恒有,即
在[1,+)上恒成立,
则必有且
(2)依题意,
即
令,
得.
则当经变化时,与变化情况如下表
1 (1,3) 3 (3,4) 4
- 0 +
-6 -18 -12
在[1,4]上的最大值是.
C.函数的图象与函数的图象恰有3个交点,即方程恰有3个不等实根.
有两个非零不等实根.
是其中一个根,
且.
存在满足条件的b的值,b的取值范围是且.
21.某企业去年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+)万元(n为正整数).
(Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为万元,进行技术改造后的累计纯利润为万元(须扣除技术改造资金),求、的表达式;
(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
【答案】(Ⅰ)依题意知,数列是一个以500为首项,-20为公差的等差数列,所以,
=
=
=
(Ⅱ)依题意得,,即,
可化简得,
可设,
又,可设是减函数,是增函数,
又
则时不等式成立,即4年
22.已知函数f(x)=loga(1+x),g(x)=loga(1-x),其中(a>0且a≠1),设h(x)=f(x)-g(x).
(1)求函数h(x)的定义域;
(2)判断h(x)的奇偶性,并说明理由;
(3)若f(3)=2,求使h(x)>0成立的x的集合.
【答案】(1)由对数的意义,分别得1+x>0,1-x>0,即x>-1,x<1.∴函数f(x)的定义域为(-1,+∞),函数g(x)的定义域为(-∞,1),
∴函数h(x)的定义域为(-1,1).
(2)∵对任意的x∈(-1,1),-x∈(-1,1),
h(-x)=f(-x)-g(-x)
=loga(1-x)-loga(1+x)
=g(x)-f(x)=-h(x),
∴h(x)是奇函数.
(3)由f(3)=2,得a=2.
此时h(x)=log2(1+x)-log2(1-x),
由h(x)>0即log2(1+x)-log2(1-x)>0,
∴log2(1+x)>log2(1-x).
由1+x>1-x>0,解得0
同课章节目录
