贵州省望谟一中2013届高三上学期8月月考文科数学试题
文档属性
| 名称 | 贵州省望谟一中2013届高三上学期8月月考文科数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 104.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-16 00:00:00 | ||
图片预览



文档简介
贵州省望谟一中2013届高三上学期8月月考文科数学试题
I 卷
一、选择题
1.若则实数的取值范围是( )
A. ;B. ;C. ;D.
【答案】B
2.已知,则的表达式为( )
B. C. D.
【答案】A
3. 如图所示的曲线是函数的大致图象,则等于( )
A. B.
C. D.
【答案】C
4.具有性质:的函数,我们称为满足“倒负”变换的函数,下列函数:
;;y= 中满足“倒负”变换的函数是( )
A. B. C. D.只有
【答案】B
5.下列四个函数中,是奇函数且在区间(-1,0)上为减函数的是( )
A. B. C. D.
【答案】D
6.函数的图象是 ( )
【答案】C
7.对于函数,以下说法正确的有 ( )
①是的函数;②对于不同的的值也不同;③表示当时函数的值,是一个常量;④一定可以用一个具体的式子表示出来。
A.1个 B.2个 C.3个 D.4个
【答案】B
8.已知函数是偶函数,则一定是函数图象的对称轴的直线是( )
A. B. C. D.
【答案】C
9.如图,有一直角墙角,两边的长度足够长,在处有一棵树与两墙的距离分别是米、4米,不考虑树的粗细.现在想用米长的
篱笆,借助墙角围成一个矩形的花圃.设此矩形花圃的面积为平方米,的最大值为,若将这棵树围在花圃内,则函数的图象大致是( )
【答案】C
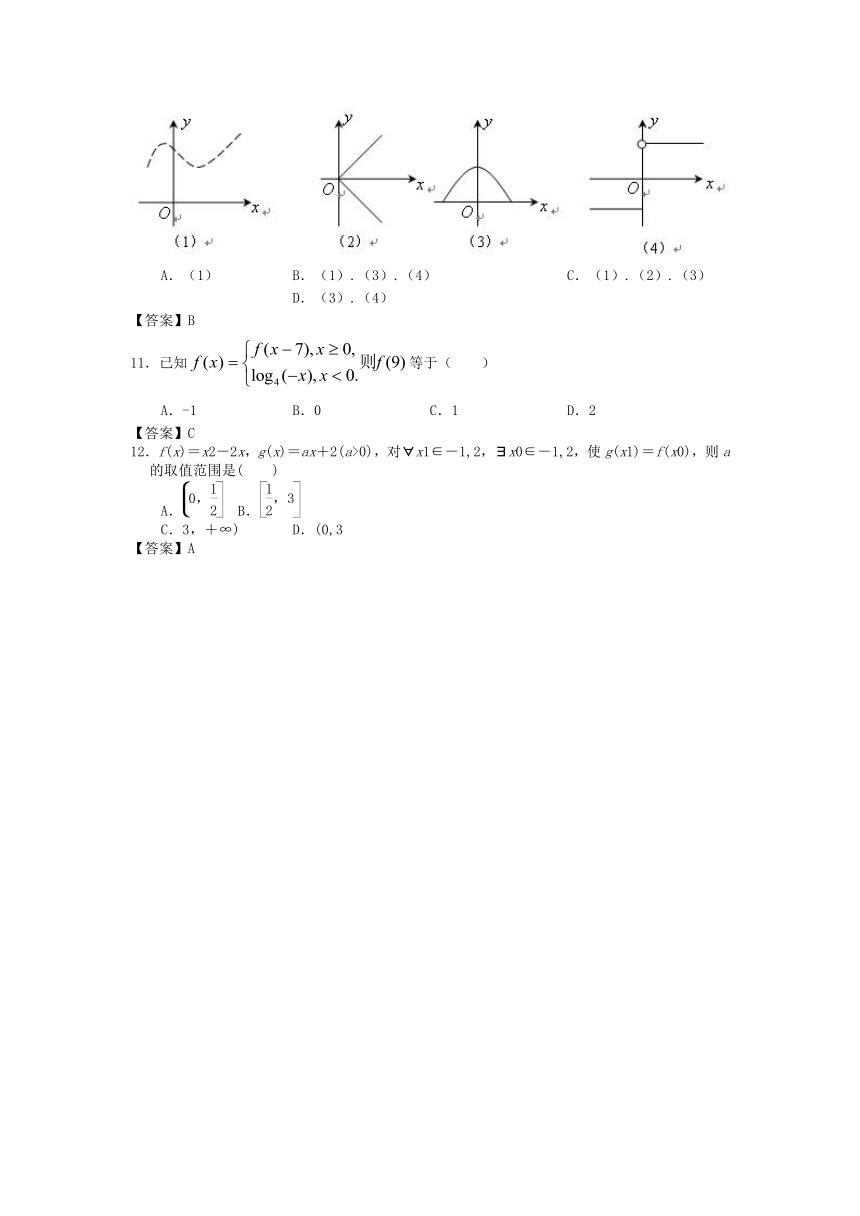
10.下列四个图像中,是函数图像的是 ( )
A.(1) B.(1).(3).(4) C.(1).(2).(3) D.(3).(4)
【答案】B
11.已知等于( )
A.-1 B.0 C.1 D.2
【答案】C
12.f(x)=x2-2x,g(x)=ax+2(a>0),对 x1∈-1,2, x0∈-1,2,使g(x1)=f(x0),则a的取值范围是( )
A. B.
C.3,+∞) D.(0,3
【答案】A
II卷
二、填空题
13.设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式<0的解集为________.
【答案】(-1,0)∪(0,1)
14.若f(x)=ax2+bx+3a+b是定义在[a-1,2a]上的偶函数,则a= ,b= .
【答案】,0
15.函数f(x)=的零点个数为________.
【答案】2
16.方程2-x+x2=3的实数解的个数为________.
【答案】2
三、解答题
17.已知函数,若存在,则称是函数的一个不动点,设
(Ⅰ)求函数的不动点;
(Ⅱ)对(Ⅰ)中的二个不动点、(假设),求使
恒成立的常数的值;
【答案】(Ⅰ)设函数
(Ⅱ)由(Ⅰ)可知
可知使恒成立的常数.
18.已知函数在定义域上为增函数,且满足
(Ⅰ) 求的值; (Ⅱ) 解不等式
【答案】(1)
(2)
而函数f(x)是定义在上为增函数
即原不等式的解集为
19.已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为元千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用,其标准如下: 7天以内(含7天),无论重量多少,均按10元天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元千克支付.
(1)当9天购买一次配料时,求该厂用于配料的保管费用P是多少元?
(2)设该厂天购买一次配料,求该厂在这天中用于配料的总费用(元)关于的函数关 系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少
【答案】(Ⅰ)当9天购买一次时,该厂用于配料的保管费用
P=70+=88(元)
(Ⅱ)(1)当x≤7时 y=360x+10x+236=370x+236
(2)当 x>7时 y=360x+236+70+6()+()+……+2+1
= ∴
∴设该厂x天购买一次配料平均每天支付的费用为f(x)元
当x≤7时 当且仅当x=7时,f(x)有最小值(元)
当x>7时=≥393
当且仅当x=12时取等号 ∵393<404 ∴当x=12时 f(x)有最小值393元
20.记函数f(x)=的定义域为A,g(x)=lg(x-a-1)(2a-x) (a<1)的定义域为B.
(1)求A;(2)若B A,求实数a的取值范围.
【答案】(1)由2-≥0,得≥0.
解上式得x<-1或x≥1,
即A=(-∞,-1)∪1,+∞).
(2)由(x-a-1)(2a-x)>0,
得(x-a-1)(x-2a)<0.
由a<1,得a+1>2a.
所以g(x)的定义域B=(2a,a+1).
又因为B A,则可得2a≥1或a+1≤-1,
即a≥或a≤-2.
因为a<1,所以≤a<1或a≤-2.
故当B A时,实数a的取值范围是
(-∞,-2∪.
21.已知函数f(x)=x+,g(x)=x+ln x,其中a>0.(1)若x=1是函数h(x)=f(x)+g(x)的极值点,求实数a的值;(2)若对任意的x1,x2∈1,e(e为自然对数的底数)都有f(x1)≥g(x2)成立,求实数a的取值范围.
【答案】 (1)∵h(x)=2x++ln x,
其定义域为(0,+∞),
∴h′(x)=2-+,
∵x=1是函数h(x)的极值点,
∴h′(1)=0,即3-a2=0.
∵a>0,∴a=.
经检验当a=时,x=1是函数h(x)的极值点,∴a=.
(2)对任意的x1,x2∈1,e都有f(x1)≥g(x2)成立等价于对任意的x1,x2∈1,e,
都有f(x)min≥g(x)max.
当x∈1,e时,g′(x)=1+>0.
∴函数g(x)=x+ln x在1,e上是增函数,
∴g(x)max=g(e)=e+1.
∵f′(x)=1-=,
且x∈1,e,a>0.
①当0<a<1且x∈1,e时,
f′(x)=>0,
∴函数f(x)=x+在1,e上是增函数,
∴f(x)min=f(1)=1+a2.
由1+a2≥e+1,得a≥,
又0<a<1,∴a不合题意.
②当1≤a≤e时,
若1≤x≤a,
则f′(x)=<0,
若a<x≤e,
则f′(x)=>0.
∴函数f(x)=x+在1,a)上是减函数,
在(a,e上是增函数.
∴f(x)min=f(a)=2a.
由2a≥e+1,得a≥.
又1≤a≤e,∴≤a≤e.
③当a>e且x∈1,e时
f′(x)=<0,
函数f(x)=x+在1,e上是减函数.
∴f(x)min=f(e)=e+.
由e+≥e+1,得a≥,
又a>e,∴a>e.
综上所述,a的取值范围为,+∞).
22.二次函数满足,且.
(1)求的解析式;
(2)在区间上,图象恒在直线上方,试确定实数取值范围.
【答案】(1)由,可设
故
由题意得,,解得;故
(2)由题意得, 即 对恒成立
设,则问题可转化为
又在上递减,故, 故
I 卷
一、选择题
1.若则实数的取值范围是( )
A. ;B. ;C. ;D.
【答案】B
2.已知,则的表达式为( )
B. C. D.
【答案】A
3. 如图所示的曲线是函数的大致图象,则等于( )
A. B.
C. D.
【答案】C
4.具有性质:的函数,我们称为满足“倒负”变换的函数,下列函数:
;;y= 中满足“倒负”变换的函数是( )
A. B. C. D.只有
【答案】B
5.下列四个函数中,是奇函数且在区间(-1,0)上为减函数的是( )
A. B. C. D.
【答案】D
6.函数的图象是 ( )
【答案】C
7.对于函数,以下说法正确的有 ( )
①是的函数;②对于不同的的值也不同;③表示当时函数的值,是一个常量;④一定可以用一个具体的式子表示出来。
A.1个 B.2个 C.3个 D.4个
【答案】B
8.已知函数是偶函数,则一定是函数图象的对称轴的直线是( )
A. B. C. D.
【答案】C
9.如图,有一直角墙角,两边的长度足够长,在处有一棵树与两墙的距离分别是米、4米,不考虑树的粗细.现在想用米长的
篱笆,借助墙角围成一个矩形的花圃.设此矩形花圃的面积为平方米,的最大值为,若将这棵树围在花圃内,则函数的图象大致是( )
【答案】C
10.下列四个图像中,是函数图像的是 ( )
A.(1) B.(1).(3).(4) C.(1).(2).(3) D.(3).(4)
【答案】B
11.已知等于( )
A.-1 B.0 C.1 D.2
【答案】C
12.f(x)=x2-2x,g(x)=ax+2(a>0),对 x1∈-1,2, x0∈-1,2,使g(x1)=f(x0),则a的取值范围是( )
A. B.
C.3,+∞) D.(0,3
【答案】A
II卷
二、填空题
13.设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式<0的解集为________.
【答案】(-1,0)∪(0,1)
14.若f(x)=ax2+bx+3a+b是定义在[a-1,2a]上的偶函数,则a= ,b= .
【答案】,0
15.函数f(x)=的零点个数为________.
【答案】2
16.方程2-x+x2=3的实数解的个数为________.
【答案】2
三、解答题
17.已知函数,若存在,则称是函数的一个不动点,设
(Ⅰ)求函数的不动点;
(Ⅱ)对(Ⅰ)中的二个不动点、(假设),求使
恒成立的常数的值;
【答案】(Ⅰ)设函数
(Ⅱ)由(Ⅰ)可知
可知使恒成立的常数.
18.已知函数在定义域上为增函数,且满足
(Ⅰ) 求的值; (Ⅱ) 解不等式
【答案】(1)
(2)
而函数f(x)是定义在上为增函数
即原不等式的解集为
19.已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为元千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用,其标准如下: 7天以内(含7天),无论重量多少,均按10元天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元千克支付.
(1)当9天购买一次配料时,求该厂用于配料的保管费用P是多少元?
(2)设该厂天购买一次配料,求该厂在这天中用于配料的总费用(元)关于的函数关 系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少
【答案】(Ⅰ)当9天购买一次时,该厂用于配料的保管费用
P=70+=88(元)
(Ⅱ)(1)当x≤7时 y=360x+10x+236=370x+236
(2)当 x>7时 y=360x+236+70+6()+()+……+2+1
= ∴
∴设该厂x天购买一次配料平均每天支付的费用为f(x)元
当x≤7时 当且仅当x=7时,f(x)有最小值(元)
当x>7时=≥393
当且仅当x=12时取等号 ∵393<404 ∴当x=12时 f(x)有最小值393元
20.记函数f(x)=的定义域为A,g(x)=lg(x-a-1)(2a-x) (a<1)的定义域为B.
(1)求A;(2)若B A,求实数a的取值范围.
【答案】(1)由2-≥0,得≥0.
解上式得x<-1或x≥1,
即A=(-∞,-1)∪1,+∞).
(2)由(x-a-1)(2a-x)>0,
得(x-a-1)(x-2a)<0.
由a<1,得a+1>2a.
所以g(x)的定义域B=(2a,a+1).
又因为B A,则可得2a≥1或a+1≤-1,
即a≥或a≤-2.
因为a<1,所以≤a<1或a≤-2.
故当B A时,实数a的取值范围是
(-∞,-2∪.
21.已知函数f(x)=x+,g(x)=x+ln x,其中a>0.(1)若x=1是函数h(x)=f(x)+g(x)的极值点,求实数a的值;(2)若对任意的x1,x2∈1,e(e为自然对数的底数)都有f(x1)≥g(x2)成立,求实数a的取值范围.
【答案】 (1)∵h(x)=2x++ln x,
其定义域为(0,+∞),
∴h′(x)=2-+,
∵x=1是函数h(x)的极值点,
∴h′(1)=0,即3-a2=0.
∵a>0,∴a=.
经检验当a=时,x=1是函数h(x)的极值点,∴a=.
(2)对任意的x1,x2∈1,e都有f(x1)≥g(x2)成立等价于对任意的x1,x2∈1,e,
都有f(x)min≥g(x)max.
当x∈1,e时,g′(x)=1+>0.
∴函数g(x)=x+ln x在1,e上是增函数,
∴g(x)max=g(e)=e+1.
∵f′(x)=1-=,
且x∈1,e,a>0.
①当0<a<1且x∈1,e时,
f′(x)=>0,
∴函数f(x)=x+在1,e上是增函数,
∴f(x)min=f(1)=1+a2.
由1+a2≥e+1,得a≥,
又0<a<1,∴a不合题意.
②当1≤a≤e时,
若1≤x≤a,
则f′(x)=<0,
若a<x≤e,
则f′(x)=>0.
∴函数f(x)=x+在1,a)上是减函数,
在(a,e上是增函数.
∴f(x)min=f(a)=2a.
由2a≥e+1,得a≥.
又1≤a≤e,∴≤a≤e.
③当a>e且x∈1,e时
f′(x)=<0,
函数f(x)=x+在1,e上是减函数.
∴f(x)min=f(e)=e+.
由e+≥e+1,得a≥,
又a>e,∴a>e.
综上所述,a的取值范围为,+∞).
22.二次函数满足,且.
(1)求的解析式;
(2)在区间上,图象恒在直线上方,试确定实数取值范围.
【答案】(1)由,可设
故
由题意得,,解得;故
(2)由题意得, 即 对恒成立
设,则问题可转化为
又在上递减,故, 故
同课章节目录
