贵州省望谟三中2013届高三上学期8月月考文科数学试题
文档属性
| 名称 | 贵州省望谟三中2013届高三上学期8月月考文科数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 106.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-16 00:00:00 | ||
图片预览



文档简介
贵州省望谟三中2013届高三上学期8月月考文科数学试题
I 卷
一、选择题
1.若与在区间1,2上都是减函数,则的取值范围是( )
A. (0,1) B. (0,1
C. (-1,0)∪(0,1) D. (-1,0) ∪(0,1
【答案】B
2. 下列判断正确的是( )
A.函数是奇函数; B.函数是偶函数
C.函数是非奇非偶函数 D.函数既是奇函数又是偶函数
【答案】C
3.设球的半径为时间t的函数。若球的体积以均匀速度c增长,则球的表面积的增长速度与球半径( )
A.成正比,比例系数为C B. 成正比,比例系数为2C
C.成反比,比例系数为C D. 成反比,比例系数为2C
【答案】D
4.定义两种运算:a b=,a b=,则f(x)=是( )
A.奇函数
B.偶函数
C.既奇又偶函数
D.非奇非偶函数
【答案】A
5.设函数则( )
A.在区间内均有零点. B.在区间内均有零点.
C.在区间内均无零点. D.在区间内内均有零点.
【答案】D
6.已知a=,b=20.3,c=0.30.2,则a,b,c三者的大小关系是( )
A.b>c>a B.b>a>c
C.a>b>c D.c>b>a
【答案】A
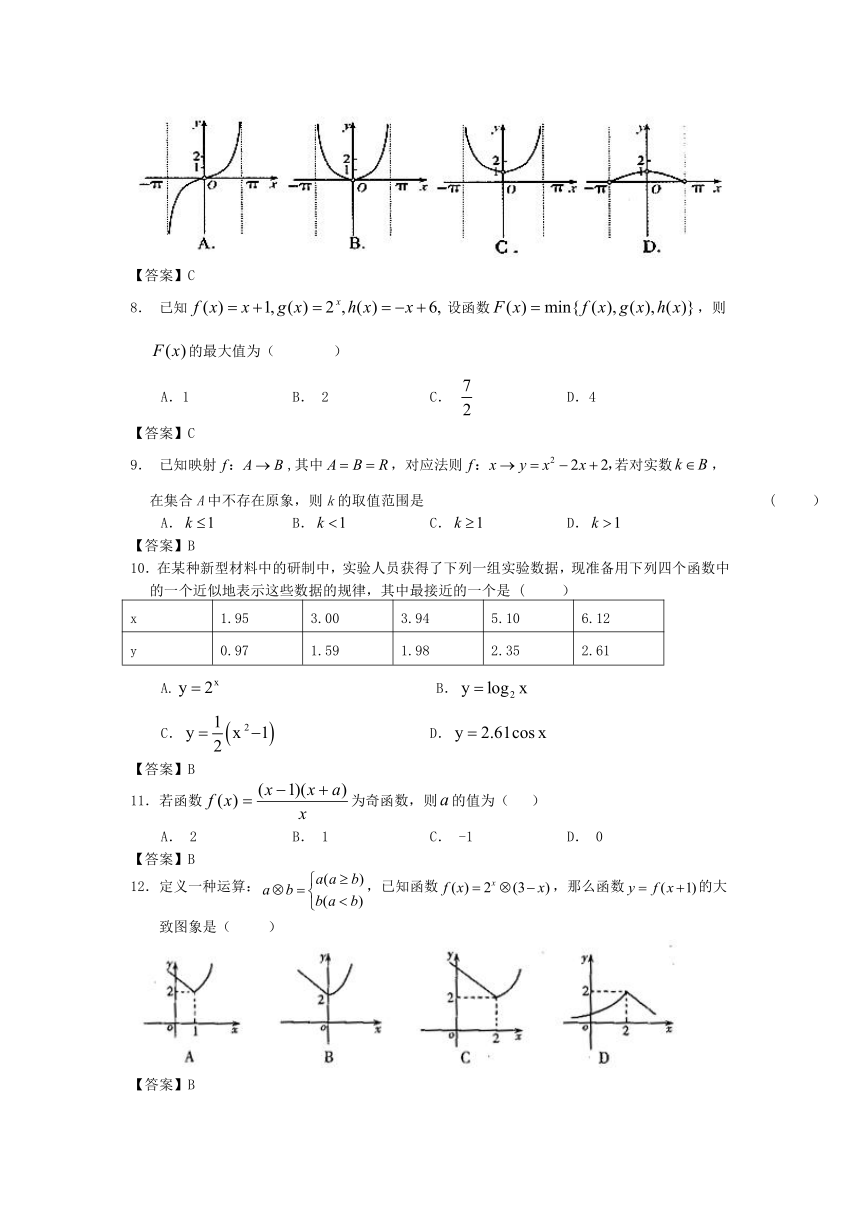
7.函数,的图象可能是下列图象中的 ( )
【答案】C
8. 已知设函数,则的最大值为( )
A.1 B. 2 C. D.4
【答案】C
9. 已知映射,其中,对应法则若对实数,在集合A中不存在原象,则k的取值范围是 ( )
A. B. C. D.
【答案】B
10.在某种新型材料中的研制中,实验人员获得了下列一组实验数据,现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是 ( )
x 1.95 3.00 3.94 5.10 6.12
y 0.97 1.59 1.98 2.35 2.61
A. B.
C. D.
【答案】B
11.若函数为奇函数,则的值为( )
A. 2 B. 1 C. -1 D. 0
【答案】B
12.定义一种运算:,已知函数,那么函数的大致图象是( )
【答案】B
II卷
二、填空题
13.设,定义P※Q=,则P※Q中元素的个数为 .
【答案】12
14.函数的定义域是 .
【答案】
15.20世纪30年代,里克特(C.F.Richter)制定了一种表明地震能量大小的尺度,就是使用地震仪测量地震能量的等级,地震能量越大,地震仪记录的地震曲线的振幅就越大,这就是我们常说的里氏震级M,其计算公式为:,其中A是被测地震的最大振幅,是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).假设在一次地震中,一个距离震中100km的测震仪记录的最大振幅是20,此时标准地震的振幅为0.001,则此次地震的震级为 (精确到0.1,已知).
【答案】4.3
16.定义在R上的函数,若对任意不等实数满足,且对于任意的,不等式成立.又函数的图象关于点(1,0)对称,则当时,的取值范围为 .
【答案】
三、解答题
17.已知函数定义域为,若对于任意的,,都有,且>0时,有>0.
⑴证明: 为奇函数;
⑵证明: 在上为单调递增函数;
⑶设=1,若<,对所有恒成立,求实数的取值范围.
【答案】(1)令,
令,,为奇函数
(2)
在上为单调递增函数;
(3)在上为单调递增函数,,使对所有恒成立,只要>1,即>0
令
18.如果函数f(x)的定义域为{x|x>0},且f(x)为增函数,f(x·y)=f(x)+f(y).
(1)求证:f()=f(x)-f(y);
(2)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围.
【答案】(1)证明:∵f(x)=f(·y)=f()+f(y),
∴f()=f(x)-f(y).
(2)∵f(3)=1,f(a)>f(a-1)+2,
∴f(a)-f(a-1)>2.
∴f()>2=f(3)+f(3)=f(9).
∵f(x)是增函数,
∴>9.又a>0,a-1>0,∴1∴a的取值范围是119.函数g(x)=x3+ax2-bx(a,b∈R),在其图象上一点P(x,y)处的切线的斜率记为f(x).
(1)若方程f(x)=0有两个实根分别为-2和4,求f(x)的表达式;
(2)若g(x)在区间-1,3上是单调递减函数,求a2+b2的最小值.
【答案】(1)f(x)=g′(x)=x2+ax-b.
∵-2,4分别是f(x)=x2+ax-b=0的两实根,
∴a=-(-2+4)=-2,b=2×4=8,
∴f(x)=x2-2x-8.
(2)∵g(x)在区间-1,3上是单调递减函数,
∴g′(x)≤0即f(x)=x2+ax-b≤0在-1,3上恒成立.
∴
即
A点坐标为(-2,3),
∴a2+b2的最小值为13.
20.已知函数满足,其中,
(1)对于函数,当时,,求实数的集合;
(2)当时,的值恒为负数,求的取值范围.
【答案】令,则.
因为
所以是R上的奇函数;
当时,,是增函数,是增函数
所以是R上的增函数;
当时,是减函数,是减函数
所以是R上的增函数;
综上所述,且时,是R上的增函数。
(1)由有
解得
(2)因为是R上的增函数,所以也是R上的增函数
由得所以
要使的值恒为负数,只需,
即
解得
又,所以的取值范围是或1<
21.某企业去年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+)万元(n为正整数).
(Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为万元,进行技术改造后的累计纯利润为万元(须扣除技术改造资金),求、的表达式;
(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
【答案】(Ⅰ)依题意知,数列是一个以500为首项,-20为公差的等差数列,所以,
=
=
=
(Ⅱ)依题意得,,即,
可化简得,
可设,
又,可设是减函数,是增函数,
又
则时不等式成立,即4年
22.已知函数f(x)=loga(1+x),g(x)=loga(1-x),其中(a>0且a≠1),设h(x)=f(x)-g(x).
(1)求函数h(x)的定义域;
(2)判断h(x)的奇偶性,并说明理由;
(3)若f(3)=2,求使h(x)>0成立的x的集合.
【答案】(1)由对数的意义,分别得1+x>0,1-x>0,即x>-1,x<1.∴函数f(x)的定义域为(-1,+∞),函数g(x)的定义域为(-∞,1),
∴函数h(x)的定义域为(-1,1).
(2)∵对任意的x∈(-1,1),-x∈(-1,1),
h(-x)=f(-x)-g(-x)
=loga(1-x)-loga(1+x)
=g(x)-f(x)=-h(x),
∴h(x)是奇函数.
(3)由f(3)=2,得a=2.
此时h(x)=log2(1+x)-log2(1-x),
由h(x)>0即log2(1+x)-log2(1-x)>0,
∴log2(1+x)>log2(1-x).
由1+x>1-x>0,解得0故使h(x)>0成立的x的集合是{x|0
I 卷
一、选择题
1.若与在区间1,2上都是减函数,则的取值范围是( )
A. (0,1) B. (0,1
C. (-1,0)∪(0,1) D. (-1,0) ∪(0,1
【答案】B
2. 下列判断正确的是( )
A.函数是奇函数; B.函数是偶函数
C.函数是非奇非偶函数 D.函数既是奇函数又是偶函数
【答案】C
3.设球的半径为时间t的函数。若球的体积以均匀速度c增长,则球的表面积的增长速度与球半径( )
A.成正比,比例系数为C B. 成正比,比例系数为2C
C.成反比,比例系数为C D. 成反比,比例系数为2C
【答案】D
4.定义两种运算:a b=,a b=,则f(x)=是( )
A.奇函数
B.偶函数
C.既奇又偶函数
D.非奇非偶函数
【答案】A
5.设函数则( )
A.在区间内均有零点. B.在区间内均有零点.
C.在区间内均无零点. D.在区间内内均有零点.
【答案】D
6.已知a=,b=20.3,c=0.30.2,则a,b,c三者的大小关系是( )
A.b>c>a B.b>a>c
C.a>b>c D.c>b>a
【答案】A
7.函数,的图象可能是下列图象中的 ( )
【答案】C
8. 已知设函数,则的最大值为( )
A.1 B. 2 C. D.4
【答案】C
9. 已知映射,其中,对应法则若对实数,在集合A中不存在原象,则k的取值范围是 ( )
A. B. C. D.
【答案】B
10.在某种新型材料中的研制中,实验人员获得了下列一组实验数据,现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是 ( )
x 1.95 3.00 3.94 5.10 6.12
y 0.97 1.59 1.98 2.35 2.61
A. B.
C. D.
【答案】B
11.若函数为奇函数,则的值为( )
A. 2 B. 1 C. -1 D. 0
【答案】B
12.定义一种运算:,已知函数,那么函数的大致图象是( )
【答案】B
II卷
二、填空题
13.设,定义P※Q=,则P※Q中元素的个数为 .
【答案】12
14.函数的定义域是 .
【答案】
15.20世纪30年代,里克特(C.F.Richter)制定了一种表明地震能量大小的尺度,就是使用地震仪测量地震能量的等级,地震能量越大,地震仪记录的地震曲线的振幅就越大,这就是我们常说的里氏震级M,其计算公式为:,其中A是被测地震的最大振幅,是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).假设在一次地震中,一个距离震中100km的测震仪记录的最大振幅是20,此时标准地震的振幅为0.001,则此次地震的震级为 (精确到0.1,已知).
【答案】4.3
16.定义在R上的函数,若对任意不等实数满足,且对于任意的,不等式成立.又函数的图象关于点(1,0)对称,则当时,的取值范围为 .
【答案】
三、解答题
17.已知函数定义域为,若对于任意的,,都有,且>0时,有>0.
⑴证明: 为奇函数;
⑵证明: 在上为单调递增函数;
⑶设=1,若<,对所有恒成立,求实数的取值范围.
【答案】(1)令,
令,,为奇函数
(2)
在上为单调递增函数;
(3)在上为单调递增函数,,使对所有恒成立,只要>1,即>0
令
18.如果函数f(x)的定义域为{x|x>0},且f(x)为增函数,f(x·y)=f(x)+f(y).
(1)求证:f()=f(x)-f(y);
(2)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围.
【答案】(1)证明:∵f(x)=f(·y)=f()+f(y),
∴f()=f(x)-f(y).
(2)∵f(3)=1,f(a)>f(a-1)+2,
∴f(a)-f(a-1)>2.
∴f()>2=f(3)+f(3)=f(9).
∵f(x)是增函数,
∴>9.又a>0,a-1>0,∴1
(1)若方程f(x)=0有两个实根分别为-2和4,求f(x)的表达式;
(2)若g(x)在区间-1,3上是单调递减函数,求a2+b2的最小值.
【答案】(1)f(x)=g′(x)=x2+ax-b.
∵-2,4分别是f(x)=x2+ax-b=0的两实根,
∴a=-(-2+4)=-2,b=2×4=8,
∴f(x)=x2-2x-8.
(2)∵g(x)在区间-1,3上是单调递减函数,
∴g′(x)≤0即f(x)=x2+ax-b≤0在-1,3上恒成立.
∴
即
A点坐标为(-2,3),
∴a2+b2的最小值为13.
20.已知函数满足,其中,
(1)对于函数,当时,,求实数的集合;
(2)当时,的值恒为负数,求的取值范围.
【答案】令,则.
因为
所以是R上的奇函数;
当时,,是增函数,是增函数
所以是R上的增函数;
当时,是减函数,是减函数
所以是R上的增函数;
综上所述,且时,是R上的增函数。
(1)由有
解得
(2)因为是R上的增函数,所以也是R上的增函数
由得所以
要使的值恒为负数,只需,
即
解得
又,所以的取值范围是或1<
21.某企业去年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+)万元(n为正整数).
(Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为万元,进行技术改造后的累计纯利润为万元(须扣除技术改造资金),求、的表达式;
(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
【答案】(Ⅰ)依题意知,数列是一个以500为首项,-20为公差的等差数列,所以,
=
=
=
(Ⅱ)依题意得,,即,
可化简得,
可设,
又,可设是减函数,是增函数,
又
则时不等式成立,即4年
22.已知函数f(x)=loga(1+x),g(x)=loga(1-x),其中(a>0且a≠1),设h(x)=f(x)-g(x).
(1)求函数h(x)的定义域;
(2)判断h(x)的奇偶性,并说明理由;
(3)若f(3)=2,求使h(x)>0成立的x的集合.
【答案】(1)由对数的意义,分别得1+x>0,1-x>0,即x>-1,x<1.∴函数f(x)的定义域为(-1,+∞),函数g(x)的定义域为(-∞,1),
∴函数h(x)的定义域为(-1,1).
(2)∵对任意的x∈(-1,1),-x∈(-1,1),
h(-x)=f(-x)-g(-x)
=loga(1-x)-loga(1+x)
=g(x)-f(x)=-h(x),
∴h(x)是奇函数.
(3)由f(3)=2,得a=2.
此时h(x)=log2(1+x)-log2(1-x),
由h(x)>0即log2(1+x)-log2(1-x)>0,
∴log2(1+x)>log2(1-x).
由1+x>1-x>0,解得0
同课章节目录
