1.3.1有理数的加法
图片预览






文档简介
(共27张PPT)
有理数
整数
分数
正整数
零
负整数
正分数
负分数
前面我们学习了有理数,有理数有几种分类方法呢?
有理数
正有理数
负有理数
正整数
零
负整数
正分数
负分数
在小学,我们学过正数与正数相加、正数与0相加。引入负数后,会出现哪些新的情况?
负数+负数
负数+正数
正数+负数
负数+0
0+负数
被加数+
加数
正数
0
负数
正数
0
负数
正数+正数
正数+0
0+正数
0+0
一个物体作左右方向的运动,我们规定
向左为负,向右为正。说出下列问题中
运动的结果,列出算式,并借助数轴
加以解释。
1.原点O是第一次运动的起点。
2.第二次运动的起点是第一次运动的终点。
3.由第二次运动的终点与原点的相对位置得出两次运动的结果。
几点说明:
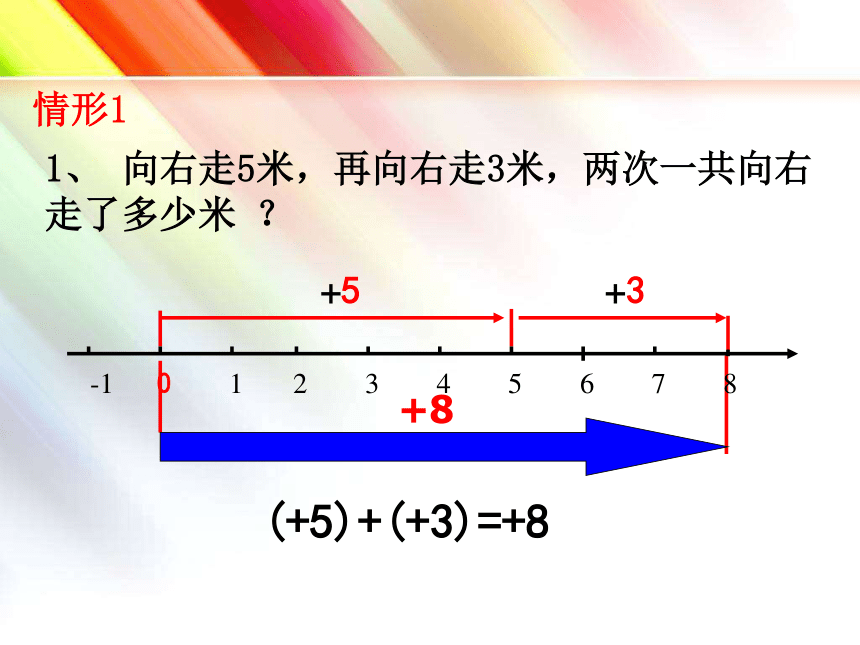
1、 向右走5米,再向右走3米,两次一共向右走了多少米 ?
(+5)+(+3)=+8
+5
+3
情形1
-1 0 1 2 3 4 5 6 7 8
+8
上面我们实际上得到的是
“正数+正数”的情况。你能模仿
上述过程,解决下面的问题吗?
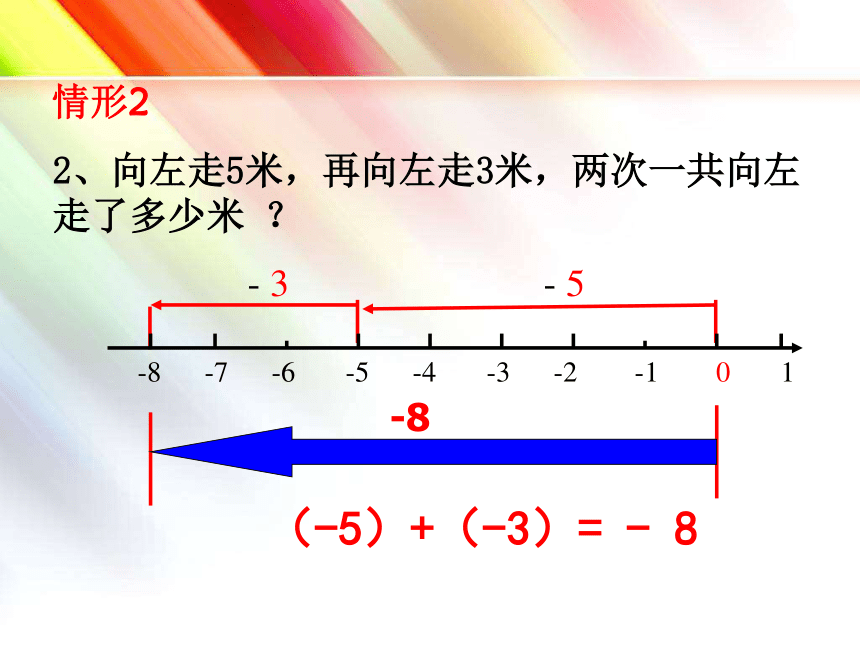
2、向左走5米,再向左走3米,两次一共向左走了多少米 ?
- 3
- 5
(-5)+(-3)= - 8
-8 -7 -6 -5 -4 -3 -2 -1 0 1
情形2
-8
( - 2 ) + (- 16 ) = - 18
( - 18 ) + (- 6 ) = - 24
(+ 3) + (+ 15) = + 18
(+7) + (+ 3) = + 10
你能从符号和绝对值两方面,用一句话概括上述两种情况吗?
并把绝对值相加
同号两数相加,取相同的符号,
这个符号是怎么来的呢?
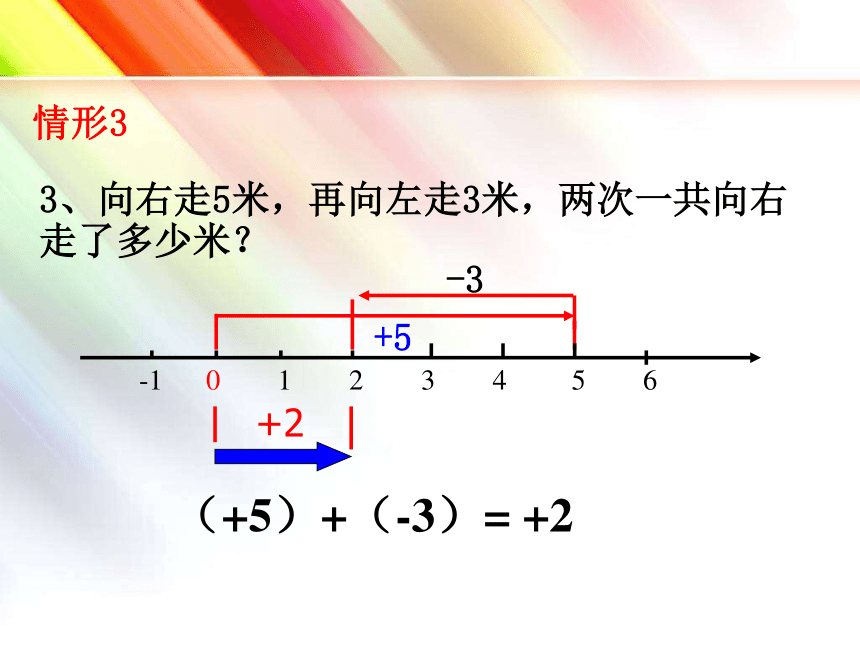
3、向右走5米,再向左走3米,两次一共向右走了多少米?
(+5)+(-3)= +2
+5
-3
-1 0 1 2 3 4 5 6
情形3
+2
4、向右走3米,再向左走5米,两次一共向右走了多少米?
(+3)+(-5)= -2
+3
-5
-3 -2 -1 0 1 2 3 4
情形4
-2
(+ 5) + ( -3 ) = + 2
(+3) + ( -5 ) = - 2
( +5) + (- 9 ) = - 4
(- 11) + (+4 ) = - 7
并用较大的绝对值减去较小的绝对值.
异号两数相加,
这个符号是怎么来的呢?
取绝对值较大的加数的符号,
类比前面的作法,你能从符号和绝对值两方面,用一句话概括上述两种情况吗?
5、向右走5米,再向左走5米,两次一共向右走了多少米?
(+5)+(-5)=0
- 5
+5
-1 0 1 2 3 4 5 6
另外两种情形
6、向左走5米,再向右走0米,两次一共向右走了多少米?
(-5)+0= - 5
-5
-5 -4 -3 -2 -1 0 1
另外两种情形
-5
(+ 5) + ( -5 ) = 0
(-3) + ( +3 ) = 0
从以下算式你能得出什么法则呢?
互为相反数的两个数相加得0;
一个数同0相加,仍得这个数.
( +5) + 0 = +5
0 + (-4 ) = - 4
(+ 5) + (+ 3) = + 8
( - 5 ) + ( - 3) = - 8
(+5) +(-3) = + 2
(+ 3) +(-5) = - 2
(+5) +(-5) = 0
(- 5)+ 0 = - 5
同号两数相加
异号两数相加
一个数与零相加
观察下面式子,你可以把有理数的加法分成几种类型?
互为相反数相加
(1)同号两数相加,取相同的符号,并把绝对值相加。
(2)异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
(3)互为相反数的两个数相加得0。
(4)一个数同0相加,仍得这个数。
你认为哪一种情况比较复杂?
有理数加法法则:
分析特征 强化理解 总结步骤
( - 4 ) + ( - 8 ) =
↓ ↓
同号两数相加
-
取相同符号
↓
( 4 + 8 )=
并把绝对值相加
↓
- 12
( - 9 ) + (+ 2)
↓ ↓
异号两数相加
= -
取绝对值较大
加数的符号
↓
( 9 - 2)
↓
并用较大的绝对值减去较小的绝对值
= -7
(1)(+3)+(-9)(2) (+8)+(+10)
例题1: 计算
解:(+8)+(+10)
解: (+3)+ (-9)
9-3
=-6
8+10
=+(18)
=-( )
=+( )
=18
1.用算式表示下面的结果:
(1)温度由-4 ℃ 上升7 ℃ ;
(2)收入7元,又支出5元.
解:(1)-4+7=3;
(2)7+(-5)=2.
2.计算:
3.直接写出结果:
(1)15 +(-22) =
(2)(-13)+(-8)=
(3)(-0.9)+ 1.5 =
(4)2.7 + (-3.5) =
比一比,看谁最巧快!
-7
-21
0.6
-0.8
4.请你用生活实例解释:
5+(-3)=2,(-5)+(-3)=-8的意义.
1、若|a|=3,|b|=2,且a、b异号,则a+b=( )A、5 B、1 C、1或-1 D、 5或-5
2、若|a|+|b|=0,则a=( ),b=( )
3、若a>0,b<0, |a|<|b|,则a+b( )0
拓展练习
小结
1、有理数的加法法则是什么?你是怎么理解这一法则的?
2.我们通过生活实例,借助数轴讨论了有理数加法法则,其中使用了哪些思考方法?
3.进行有理数的加法运算时需要注意哪几个步骤?
作业:
教科书习题1.3
第1,8,9题
有理数
整数
分数
正整数
零
负整数
正分数
负分数
前面我们学习了有理数,有理数有几种分类方法呢?
有理数
正有理数
负有理数
正整数
零
负整数
正分数
负分数
在小学,我们学过正数与正数相加、正数与0相加。引入负数后,会出现哪些新的情况?
负数+负数
负数+正数
正数+负数
负数+0
0+负数
被加数+
加数
正数
0
负数
正数
0
负数
正数+正数
正数+0
0+正数
0+0
一个物体作左右方向的运动,我们规定
向左为负,向右为正。说出下列问题中
运动的结果,列出算式,并借助数轴
加以解释。
1.原点O是第一次运动的起点。
2.第二次运动的起点是第一次运动的终点。
3.由第二次运动的终点与原点的相对位置得出两次运动的结果。
几点说明:
1、 向右走5米,再向右走3米,两次一共向右走了多少米 ?
(+5)+(+3)=+8
+5
+3
情形1
-1 0 1 2 3 4 5 6 7 8
+8
上面我们实际上得到的是
“正数+正数”的情况。你能模仿
上述过程,解决下面的问题吗?
2、向左走5米,再向左走3米,两次一共向左走了多少米 ?
- 3
- 5
(-5)+(-3)= - 8
-8 -7 -6 -5 -4 -3 -2 -1 0 1
情形2
-8
( - 2 ) + (- 16 ) = - 18
( - 18 ) + (- 6 ) = - 24
(+ 3) + (+ 15) = + 18
(+7) + (+ 3) = + 10
你能从符号和绝对值两方面,用一句话概括上述两种情况吗?
并把绝对值相加
同号两数相加,取相同的符号,
这个符号是怎么来的呢?
3、向右走5米,再向左走3米,两次一共向右走了多少米?
(+5)+(-3)= +2
+5
-3
-1 0 1 2 3 4 5 6
情形3
+2
4、向右走3米,再向左走5米,两次一共向右走了多少米?
(+3)+(-5)= -2
+3
-5
-3 -2 -1 0 1 2 3 4
情形4
-2
(+ 5) + ( -3 ) = + 2
(+3) + ( -5 ) = - 2
( +5) + (- 9 ) = - 4
(- 11) + (+4 ) = - 7
并用较大的绝对值减去较小的绝对值.
异号两数相加,
这个符号是怎么来的呢?
取绝对值较大的加数的符号,
类比前面的作法,你能从符号和绝对值两方面,用一句话概括上述两种情况吗?
5、向右走5米,再向左走5米,两次一共向右走了多少米?
(+5)+(-5)=0
- 5
+5
-1 0 1 2 3 4 5 6
另外两种情形
6、向左走5米,再向右走0米,两次一共向右走了多少米?
(-5)+0= - 5
-5
-5 -4 -3 -2 -1 0 1
另外两种情形
-5
(+ 5) + ( -5 ) = 0
(-3) + ( +3 ) = 0
从以下算式你能得出什么法则呢?
互为相反数的两个数相加得0;
一个数同0相加,仍得这个数.
( +5) + 0 = +5
0 + (-4 ) = - 4
(+ 5) + (+ 3) = + 8
( - 5 ) + ( - 3) = - 8
(+5) +(-3) = + 2
(+ 3) +(-5) = - 2
(+5) +(-5) = 0
(- 5)+ 0 = - 5
同号两数相加
异号两数相加
一个数与零相加
观察下面式子,你可以把有理数的加法分成几种类型?
互为相反数相加
(1)同号两数相加,取相同的符号,并把绝对值相加。
(2)异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
(3)互为相反数的两个数相加得0。
(4)一个数同0相加,仍得这个数。
你认为哪一种情况比较复杂?
有理数加法法则:
分析特征 强化理解 总结步骤
( - 4 ) + ( - 8 ) =
↓ ↓
同号两数相加
-
取相同符号
↓
( 4 + 8 )=
并把绝对值相加
↓
- 12
( - 9 ) + (+ 2)
↓ ↓
异号两数相加
= -
取绝对值较大
加数的符号
↓
( 9 - 2)
↓
并用较大的绝对值减去较小的绝对值
= -7
(1)(+3)+(-9)(2) (+8)+(+10)
例题1: 计算
解:(+8)+(+10)
解: (+3)+ (-9)
9-3
=-6
8+10
=+(18)
=-( )
=+( )
=18
1.用算式表示下面的结果:
(1)温度由-4 ℃ 上升7 ℃ ;
(2)收入7元,又支出5元.
解:(1)-4+7=3;
(2)7+(-5)=2.
2.计算:
3.直接写出结果:
(1)15 +(-22) =
(2)(-13)+(-8)=
(3)(-0.9)+ 1.5 =
(4)2.7 + (-3.5) =
比一比,看谁最巧快!
-7
-21
0.6
-0.8
4.请你用生活实例解释:
5+(-3)=2,(-5)+(-3)=-8的意义.
1、若|a|=3,|b|=2,且a、b异号,则a+b=( )A、5 B、1 C、1或-1 D、 5或-5
2、若|a|+|b|=0,则a=( ),b=( )
3、若a>0,b<0, |a|<|b|,则a+b( )0
拓展练习
小结
1、有理数的加法法则是什么?你是怎么理解这一法则的?
2.我们通过生活实例,借助数轴讨论了有理数加法法则,其中使用了哪些思考方法?
3.进行有理数的加法运算时需要注意哪几个步骤?
作业:
教科书习题1.3
第1,8,9题
