江西省赣州市潭口高级中学2021-2022学年高一上学期10月月考数学试卷(Word版含答案)
文档属性
| 名称 | 江西省赣州市潭口高级中学2021-2022学年高一上学期10月月考数学试卷(Word版含答案) | 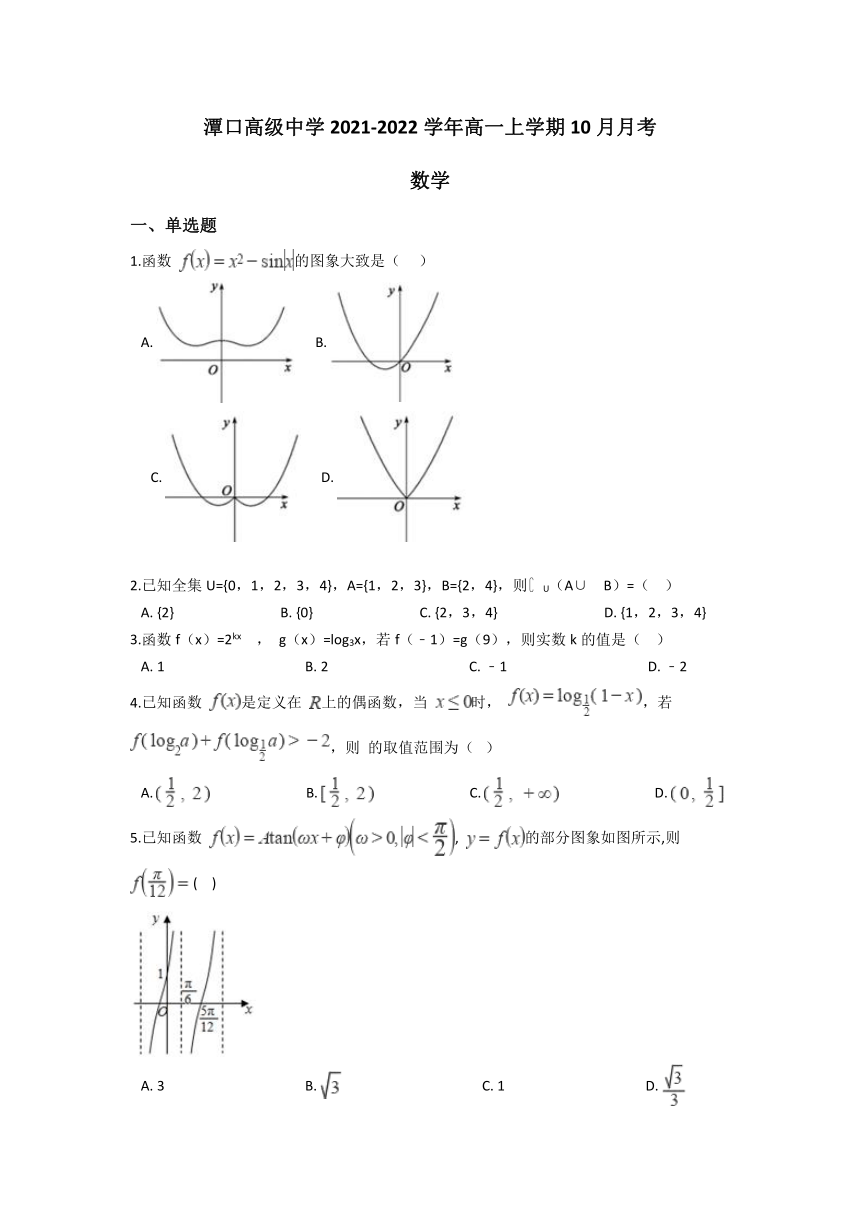 | |
| 格式 | doc | ||
| 文件大小 | 362.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 20:20:45 | ||
图片预览



文档简介
潭口高级中学2021-2022学年高一上学期10月月考
数学
一、单选题
1.函数 的图象大致是( )
A. B.
C. D.
2.已知全集U={0,1,2,3,4},A={1,2,3},B={2,4},则 U(A∪ B)=( )
A. {2} B. {0} C. {2,3,4} D. {1,2,3,4}
3.函数f(x)=2kx , g(x)=log3x,若f(﹣1)=g(9),则实数k的值是( )
A. 1 B. 2 C. ﹣1 D. ﹣2
4.已知函数 是定义在 上的偶函数,当 时, ,若 ,则 的取值范围为( )
A. B. C. D.
5.已知函数 , 的部分图象如图所示,则 ( )
A. 3 B. C. 1 D.
6.已知奇函数f(x)的定义域为 且 是f(x)的导函数.若对任意 都有 则满足 的θ的取值范围是( )
A. B. C. D.
7.若函数有两个零点, 其中, 那么在两个函数值中 ( )
A. 只有一个小于1 B. 至少有一个小于1 C. 都小于1 D. 可能都大于1
8.若函数在区间内单调递增,则a取值范围是( )
A. [, 1) B. [, 1) C. D. (1,)
二、多选题
9.若函数 的定义域为 且为奇函数,则 可能的值为( )
A. -1 B. 1 C. D. 3
10.设函数 是定义在 上的偶函数,且对任意的 恒有 ,已知当 时, ,则下列说法正确的是( )
A. 3是函数 的周期 B. 函数 在 上递减,在 上递增
C. 函数 的最大值为 ,最小值为0 D. 当 时,
11.在平面直角坐标系中,曲线 上任意点 与两个定点 和点 连线的斜率之和等于2,则关于曲线 的结论正确的有( )
A. 曲线 是轴对称图形 B. 曲线 上所有的点都在圆 外
C. 曲线 是中心对称图形 D. 曲线 上所有点的横坐标 满足
12.已知 , 均为正实数,若 , ,则 ( )
A. B. C. D. 2
三、填空题
13.函数y= 的定义域为 .
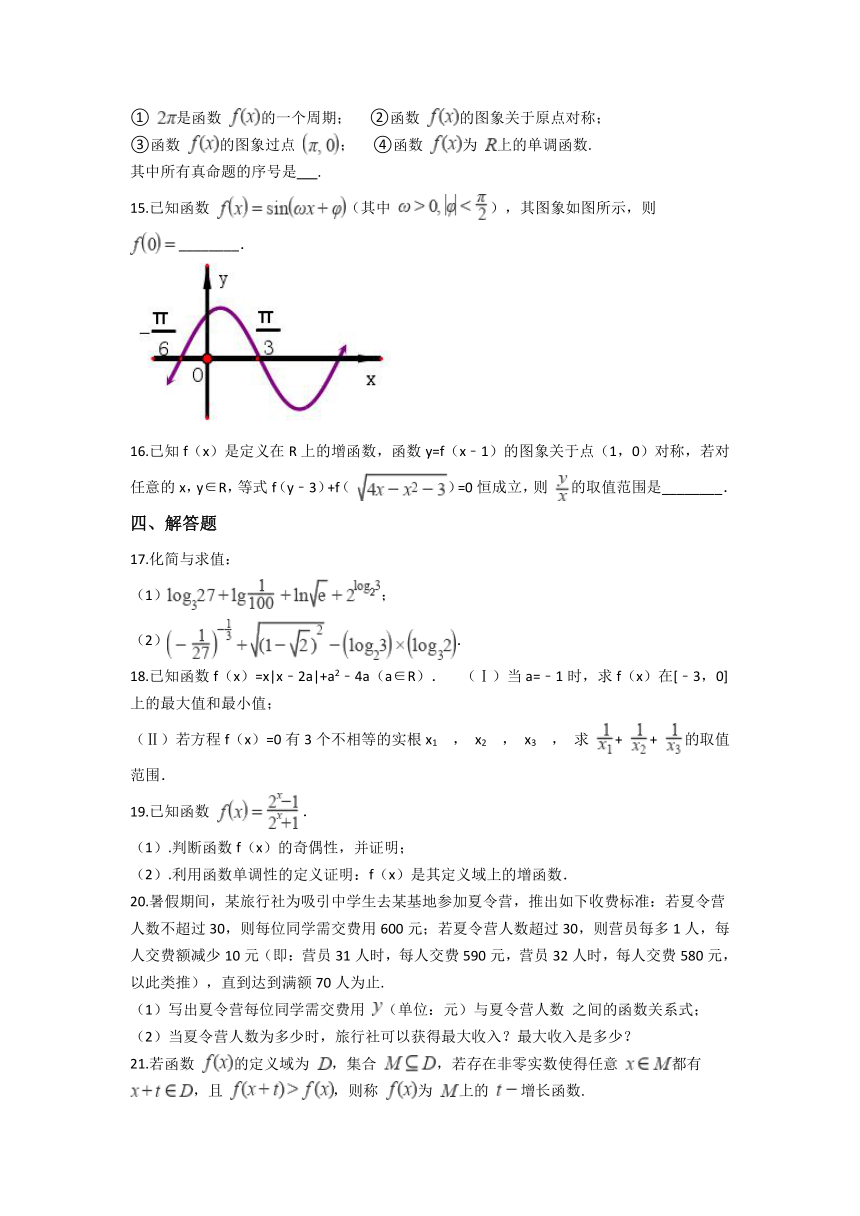
14.已知函数 ,给出下列四个命题:
① 是函数 的一个周期; ②函数 的图象关于原点对称;
③函数 的图象过点 ; ④函数 为 上的单调函数.
其中所有真命题的序号是 .
15.已知函数 (其中 ),其图象如图所示,则 ________.
16.已知f(x)是定义在R上的增函数,函数y=f(x﹣1)的图象关于点(1,0)对称,若对任意的x,y∈R,等式f(y﹣3)+f( )=0恒成立,则 的取值范围是________.
四、解答题
17.化简与求值:
(1);
(2).
18.已知函数f(x)=x|x﹣2a|+a2﹣4a(a∈R). (Ⅰ)当a=﹣1时,求f(x)在[﹣3,0]上的最大值和最小值;
(Ⅱ)若方程f(x)=0有3个不相等的实根x1 , x2 , x3 , 求 + + 的取值范围.
19.已知函数 .
(1).判断函数f(x)的奇偶性,并证明;
(2).利用函数单调性的定义证明:f(x)是其定义域上的增函数.
20.暑假期间,某旅行社为吸引中学生去某基地参加夏令营,推出如下收费标准:若夏令营人数不超过30,则每位同学需交费用600元;若夏令营人数超过30,则营员每多1人,每人交费额减少10元(即:营员31人时,每人交费590元,营员32人时,每人交费580元,以此类推),直到达到满额70人为止.
(1)写出夏令营每位同学需交费用 (单位:元)与夏令营人数 之间的函数关系式;
(2)当夏令营人数为多少时,旅行社可以获得最大收入?最大收入是多少?
21.若函数 的定义域为 ,集合 ,若存在非零实数使得任意 都有 ,且 ,则称 为 上的 增长函数.
(1)已知函数 ,函数 ,判断 和 是否为区间 上的 增长函数,并说明理由;
(2)已知函数 ,且 是区间 上的 增长函数,求正整数 的最小值;
(3)请在以下两个问题中任选一个作答:(如果两问都做,按(i)得分计入总分)
(i)如果对任意正有理数 , 都是 上的 增长函数,判断 是否一定为 上的单调递增函数,并说明理由;
(ii)如果 是定义域为 的奇函数,当 时, ,且 为 上的 增长函数,求实数 的取值范围.
22.在平面直角坐标系中, 为坐标原点, , , 三点满足 .
(1)求 值;
(2)已知 若 的最小值为 ,求 的最大值.
答案部分
一、单选题
1.【答案】 C
2.【答案】B
3.【答案】C
4.【答案】 A
5.【答案】 A
6.【答案】 D
7.【答案】 B
8.【答案】 B
二、多选题
9.【答案】 B,D
10.【答案】 A,B
11.【答案】 B,C
12.【答案】 A,D
三、填空题
13.【答案】 (2,3)∪(3,+∞)
14.【答案】 ①②③
15.【答案】
16.【答案】
四、解答题
17.【答案】 (1)解: =3﹣2 3 ;
(2)解:
.
18.【答案】解:(Ⅰ)∵a=﹣1, ∴f(x)=x|x+2|+5= ,
x∈[﹣2,0]时,4≤f(x)≤5,
x∈[﹣3,﹣2]时,2≤f(x)≤5,
∴f(x)min=f(﹣3)=2,f(x)max=f(0)=5;
(Ⅱ)∵f(x)= ,
①若a>0,∵方程f(x)=0有3个不相等的实根,
故x<2a时,方程f(x)=﹣x2+2ax+a2﹣4a=0有2个不相等的实根,
x≥2a时,方程f(x)=x2﹣2ax+a2﹣4a=0有1个不相等的实根,
∴ ,解得:2<a<4,
不妨设x1<x2<x3 , 则x1+x2=2a,x1x2=﹣a2+4a,x3=a+2 ,
∴ + + = + =﹣ > ,
∴ + + 的范围是( ,+∞),
②若a<0,当x>2a时,方程f(x)=x2﹣2ax+a2﹣4a=0的判别式小于0,
不符合题意;
③a=0时,显然不和题意,
故 + + 的范围是( ,+∞)
19.【答案】 (1)解:f(x)为奇函数.证明如下:
∵2x+1≠0,
∴f(x)的定义域为R,
又∵ ,
∴f(x)为奇函数
(2)解: ,
任取x1、x2∈R,设x1<x2 ,
∵ = = ,
∵ ,∴ ,又 , ,
∴f(x1)﹣f(x2)<0,∴f(x1)<f(x2).
∴f(x)在其定义域R上是增函数
20.【答案】 (1)解:由题意可知每人需交费 关于人数 的函数:
(2)解:旅行社收入为 ,则 ,
即 ,
当 时, 为增函数,
所以 ,
当 时, 为开口向下的二次函数,
对称轴 ,所以在对称轴处取得最大值, .
综上所述:当人数为45人时,最大收入为20250元
21.【答案】 (1)解: 是;因为 , ;
不是,反例:当 时, .
(2)解:由题意得, 对 恒成立
等价于 ,即 对 恒成立
因为 ,所以 是关于 的一次函数且单调递增,于是只需 ,
解得 ,所以满足题意的最小正整数 为9.
(3)解:(i)不是
构造 ,则对任意正有理数 ,
若 ,则 ,因此 ;
若 ,则 ,因此 .
因此 是 上的 -增长函数,但 不是增函数.
(ii)由题意知
已知任意 , ,
因为 在 上递减,所以 不能同时在区间 上,
因此
注意到 在 上非负,在 上非正
若 ,当 时, ,此时 ,矛盾
因此 ,即 .
当 时,下证 为 上的 -增长函数:
①当 , 显然成立
②当 时, ,此时 , ,
③当 时,
因此 为 上的 -增长函数
综上,为使得 为 上的 -增长函数 的取值范围是 .
22.【答案】 (1)解:由题意知 三点满足 ,
可得 ,所以 ,即
即 ,则 ,所以
(2)解:由题意,函数
因为 ,所以 ,
当 时, 取得最小值 ,
当 时,当 时, 取得最小值 ,
当 时,当 时, 取得最小值 ,
综上所述, ,可得函数 的最大值为1,
即 的最大值为1
数学
一、单选题
1.函数 的图象大致是( )
A. B.
C. D.
2.已知全集U={0,1,2,3,4},A={1,2,3},B={2,4},则 U(A∪ B)=( )
A. {2} B. {0} C. {2,3,4} D. {1,2,3,4}
3.函数f(x)=2kx , g(x)=log3x,若f(﹣1)=g(9),则实数k的值是( )
A. 1 B. 2 C. ﹣1 D. ﹣2
4.已知函数 是定义在 上的偶函数,当 时, ,若 ,则 的取值范围为( )
A. B. C. D.
5.已知函数 , 的部分图象如图所示,则 ( )
A. 3 B. C. 1 D.
6.已知奇函数f(x)的定义域为 且 是f(x)的导函数.若对任意 都有 则满足 的θ的取值范围是( )
A. B. C. D.
7.若函数有两个零点, 其中, 那么在两个函数值中 ( )
A. 只有一个小于1 B. 至少有一个小于1 C. 都小于1 D. 可能都大于1
8.若函数在区间内单调递增,则a取值范围是( )
A. [, 1) B. [, 1) C. D. (1,)
二、多选题
9.若函数 的定义域为 且为奇函数,则 可能的值为( )
A. -1 B. 1 C. D. 3
10.设函数 是定义在 上的偶函数,且对任意的 恒有 ,已知当 时, ,则下列说法正确的是( )
A. 3是函数 的周期 B. 函数 在 上递减,在 上递增
C. 函数 的最大值为 ,最小值为0 D. 当 时,
11.在平面直角坐标系中,曲线 上任意点 与两个定点 和点 连线的斜率之和等于2,则关于曲线 的结论正确的有( )
A. 曲线 是轴对称图形 B. 曲线 上所有的点都在圆 外
C. 曲线 是中心对称图形 D. 曲线 上所有点的横坐标 满足
12.已知 , 均为正实数,若 , ,则 ( )
A. B. C. D. 2
三、填空题
13.函数y= 的定义域为 .
14.已知函数 ,给出下列四个命题:
① 是函数 的一个周期; ②函数 的图象关于原点对称;
③函数 的图象过点 ; ④函数 为 上的单调函数.
其中所有真命题的序号是 .
15.已知函数 (其中 ),其图象如图所示,则 ________.
16.已知f(x)是定义在R上的增函数,函数y=f(x﹣1)的图象关于点(1,0)对称,若对任意的x,y∈R,等式f(y﹣3)+f( )=0恒成立,则 的取值范围是________.
四、解答题
17.化简与求值:
(1);
(2).
18.已知函数f(x)=x|x﹣2a|+a2﹣4a(a∈R). (Ⅰ)当a=﹣1时,求f(x)在[﹣3,0]上的最大值和最小值;
(Ⅱ)若方程f(x)=0有3个不相等的实根x1 , x2 , x3 , 求 + + 的取值范围.
19.已知函数 .
(1).判断函数f(x)的奇偶性,并证明;
(2).利用函数单调性的定义证明:f(x)是其定义域上的增函数.
20.暑假期间,某旅行社为吸引中学生去某基地参加夏令营,推出如下收费标准:若夏令营人数不超过30,则每位同学需交费用600元;若夏令营人数超过30,则营员每多1人,每人交费额减少10元(即:营员31人时,每人交费590元,营员32人时,每人交费580元,以此类推),直到达到满额70人为止.
(1)写出夏令营每位同学需交费用 (单位:元)与夏令营人数 之间的函数关系式;
(2)当夏令营人数为多少时,旅行社可以获得最大收入?最大收入是多少?
21.若函数 的定义域为 ,集合 ,若存在非零实数使得任意 都有 ,且 ,则称 为 上的 增长函数.
(1)已知函数 ,函数 ,判断 和 是否为区间 上的 增长函数,并说明理由;
(2)已知函数 ,且 是区间 上的 增长函数,求正整数 的最小值;
(3)请在以下两个问题中任选一个作答:(如果两问都做,按(i)得分计入总分)
(i)如果对任意正有理数 , 都是 上的 增长函数,判断 是否一定为 上的单调递增函数,并说明理由;
(ii)如果 是定义域为 的奇函数,当 时, ,且 为 上的 增长函数,求实数 的取值范围.
22.在平面直角坐标系中, 为坐标原点, , , 三点满足 .
(1)求 值;
(2)已知 若 的最小值为 ,求 的最大值.
答案部分
一、单选题
1.【答案】 C
2.【答案】B
3.【答案】C
4.【答案】 A
5.【答案】 A
6.【答案】 D
7.【答案】 B
8.【答案】 B
二、多选题
9.【答案】 B,D
10.【答案】 A,B
11.【答案】 B,C
12.【答案】 A,D
三、填空题
13.【答案】 (2,3)∪(3,+∞)
14.【答案】 ①②③
15.【答案】
16.【答案】
四、解答题
17.【答案】 (1)解: =3﹣2 3 ;
(2)解:
.
18.【答案】解:(Ⅰ)∵a=﹣1, ∴f(x)=x|x+2|+5= ,
x∈[﹣2,0]时,4≤f(x)≤5,
x∈[﹣3,﹣2]时,2≤f(x)≤5,
∴f(x)min=f(﹣3)=2,f(x)max=f(0)=5;
(Ⅱ)∵f(x)= ,
①若a>0,∵方程f(x)=0有3个不相等的实根,
故x<2a时,方程f(x)=﹣x2+2ax+a2﹣4a=0有2个不相等的实根,
x≥2a时,方程f(x)=x2﹣2ax+a2﹣4a=0有1个不相等的实根,
∴ ,解得:2<a<4,
不妨设x1<x2<x3 , 则x1+x2=2a,x1x2=﹣a2+4a,x3=a+2 ,
∴ + + = + =﹣ > ,
∴ + + 的范围是( ,+∞),
②若a<0,当x>2a时,方程f(x)=x2﹣2ax+a2﹣4a=0的判别式小于0,
不符合题意;
③a=0时,显然不和题意,
故 + + 的范围是( ,+∞)
19.【答案】 (1)解:f(x)为奇函数.证明如下:
∵2x+1≠0,
∴f(x)的定义域为R,
又∵ ,
∴f(x)为奇函数
(2)解: ,
任取x1、x2∈R,设x1<x2 ,
∵ = = ,
∵ ,∴ ,又 , ,
∴f(x1)﹣f(x2)<0,∴f(x1)<f(x2).
∴f(x)在其定义域R上是增函数
20.【答案】 (1)解:由题意可知每人需交费 关于人数 的函数:
(2)解:旅行社收入为 ,则 ,
即 ,
当 时, 为增函数,
所以 ,
当 时, 为开口向下的二次函数,
对称轴 ,所以在对称轴处取得最大值, .
综上所述:当人数为45人时,最大收入为20250元
21.【答案】 (1)解: 是;因为 , ;
不是,反例:当 时, .
(2)解:由题意得, 对 恒成立
等价于 ,即 对 恒成立
因为 ,所以 是关于 的一次函数且单调递增,于是只需 ,
解得 ,所以满足题意的最小正整数 为9.
(3)解:(i)不是
构造 ,则对任意正有理数 ,
若 ,则 ,因此 ;
若 ,则 ,因此 .
因此 是 上的 -增长函数,但 不是增函数.
(ii)由题意知
已知任意 , ,
因为 在 上递减,所以 不能同时在区间 上,
因此
注意到 在 上非负,在 上非正
若 ,当 时, ,此时 ,矛盾
因此 ,即 .
当 时,下证 为 上的 -增长函数:
①当 , 显然成立
②当 时, ,此时 , ,
③当 时,
因此 为 上的 -增长函数
综上,为使得 为 上的 -增长函数 的取值范围是 .
22.【答案】 (1)解:由题意知 三点满足 ,
可得 ,所以 ,即
即 ,则 ,所以
(2)解:由题意,函数
因为 ,所以 ,
当 时, 取得最小值 ,
当 时,当 时, 取得最小值 ,
当 时,当 时, 取得最小值 ,
综上所述, ,可得函数 的最大值为1,
即 的最大值为1
同课章节目录
