第四章图形的相似 单元测试训练卷 2021-2022学年北师大版九年级数学上册(Word版含答案)
文档属性
| 名称 | 第四章图形的相似 单元测试训练卷 2021-2022学年北师大版九年级数学上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 214.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 10:11:32 | ||
图片预览


文档简介
北师版九年级数学上册
第四章 图形的相似
单元测试训练卷
一、选择题(共8小题,4*8=32)
1. 下列说法正确的是( )
A.若=,则a=b B.若-x=4y,则x=-2y
C.若ax=bx,则a=b D.若a2=b2,则a=b
2. 已知线段AB,在BA的延长线上取一点C,使CA=3AB,则线段CA与线段CB的比为( )
A.3:4 B.2:3
C.3:5 D.1:2
3. 如图,正五边形FGHMN与正五边形ABCDE相似,若AB:FG=2:3,则下列结论正确的是( )
A.2DE=3MN B.3DE=2MN
C.3∠A=2∠F D.2∠A=3∠F
4. 如图,D是△ABC的边AB上一点,要使△ACD∽△ABC,则必须具备的条件可以是( )
A.= B.=
C.CD2=AD·DB D.AC2=AD·AB
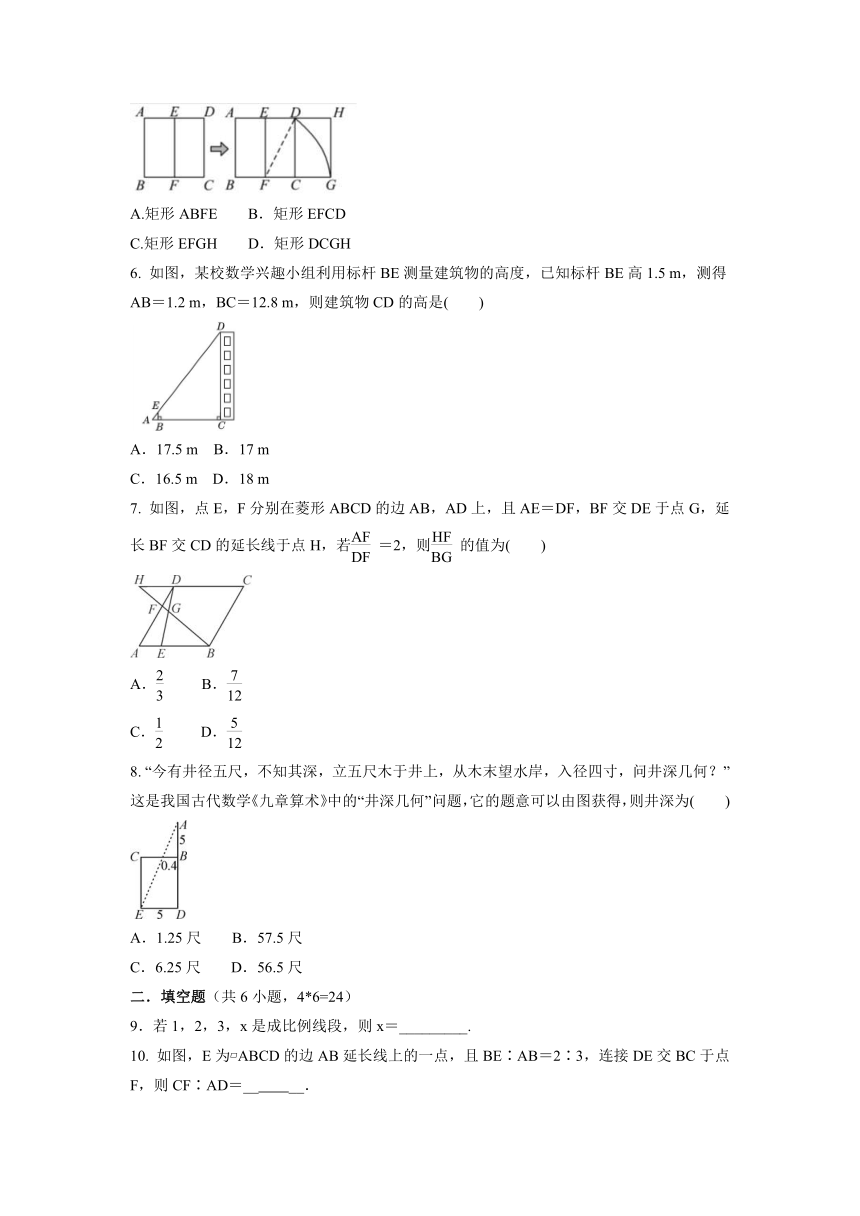
5. 宽与长的比是(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD,BC的中点E,F,连接EF;以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是( )
A.矩形ABFE B.矩形EFCD
C.矩形EFGH D.矩形DCGH
6. 如图,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5 m,测得AB=1.2 m,BC=12.8 m,则建筑物CD的高是( )
A.17.5 m B.17 m
C.16.5 m D.18 m
7. 如图,点E,F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于点H,若=2,则的值为( )
A. B.
C. D.
8. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A.1.25尺 B.57.5尺
C.6.25尺 D.56.5尺
二.填空题(共6小题,4*6=24)
9.若1,2,3,x是成比例线段,则x=_________.
10. 如图,E为 ABCD的边AB延长线上的一点,且BE∶AB=2∶3,连接DE交BC于点F,则CF∶AD=__ __.
,
11. 如图,在△ABC中,DE∥AB,且=,则的值为________.
12. 主持人主持节目时,站在舞台的黄金分割点处最自然得体.如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她至少走__________米才最理想.
13. 如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆,小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为__ __米.
14. 如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且=,若点A(-1,0),点C(,1),则A′C′=_______.
三.解答题(共5小题, 44分)
15.(6分) 如图,在△ABC中,AD是中线,且CD2=BE·BA.求证:ED·AB=AD·BD.
16.(8分) 如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场上的旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶端A在同一直线上.已知DE=0.5 m,EF=0.25 m,目测点D到地面的距离DG=1.5 m,到旗杆的水平距离DC=20 m ,求旗杆的高度.
17.(8分) )如图,在四边形ABCD中,AB∥CD,连接BD,AB=8,BD=12,CD=18.
(1)求证:△ABD∽△BDC;
(2)若△ABD的面积为40,求四边形ABCD的面积.
18.(10分) 如图,已知△ABC,∠BAC的平分线与△ABC的外角∠DAC的平分线分别交BC及BC的延长线于点P,Q.
(1)求∠PAQ的度数;
(2)若点M为PQ的中点,连接AM,求证:PM2=CM·BM.
19.(12分) 如图,在矩形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.
(1)如图①,当=时,求的值;
(2)如图②,当=时,求AF与OA的比值(用含m的代数式表示);
(3)如图③,当=时,过点F作FG⊥BC于点G,探索EG与BG的数量关系(用含m的代数式表示),并说明理由.
参考答案
1-4AABD 5-8DABB
9.6
10.3∶5
11.
12.18-6
13.22.5
14.
15.证明:∵AD是中线,∴BD=CD.又CD2=BE·BA,∴BD2=BE·BA,即=,又∠B=∠B,∴△BED∽△BDA,∴=,∴ED·AB=AD·BD.
16.解:∵∠DEF=∠DCA=90°,∠EDF=∠CDA,∴△DEF∽△DCA.∴=.∵DE=0.5 m,EF=0.25 m,DC=20 m,∴=.∴AC=10 m.又∵CB=DG=1.5 m,∴AB=AC+CB=10+1.5=11.5(m).答:旗杆的高度为11.5 m.
17.解:(1)证明:∵AB∥CD,∴∠ABD=∠BDC.∵AB=8,BD=12,CD=18,∴==,∴△ABD∽△BDC
(2)∵△ABD∽△BDC,=,∴=()2=.又∵△ABD的面积为40,∴S△BDC=90,∴四边形ABCD的面积为40+90=130
18.解:∵AP平分∠BAC,∴∠PAC=∠BAC.∵AQ平分∠CAD,∴∠CAQ=∠CAD.
∴∠PAC+∠CAQ=∠BAC+∠CAD=(∠BAC+∠CAD).又∵∠BAC+∠CAD=180°,∴∠PAC+∠CAQ=90°,即∠PAQ=90°.
(2)证明:由(1)知∠PAQ=90°.∵M是PQ的中点,∴PM=AM.∴∠APM=∠PAM.∵∠APM=∠B+∠BAP,∠PAM=∠CAM+∠PAC,∠BAP=∠PAC,∴∠CAM=∠B.又∵∠AMC=∠BMA,∴△ACM∽△BAM. ∴=.∴AM2=CM·BM,即PM2=CM·BM.
19.解:(1)∵=,∴=,∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∴△CEF∽△ADF,∴=,∴==,==
(2)设EC=1,则BE=m,∵四边形ABCD是矩形,∴AD∥BC,AD=BC=m+1,∴△CEF∽△ADF,∴==,∴=,∵=,∴AC=2OA,∴=,∴=
(3)结论:=()2,理由:设EC=1,则BE=m,∵四边形ABCD是矩形,∴AD∥BC,AD=BC=m+1,∴△CEF∽△ADF,∴===,∵FG⊥BC,∴FG∥CD,∴==,①∵FG∥AB,∴==,②由①×②,可得×=×,即=()2
第四章 图形的相似
单元测试训练卷
一、选择题(共8小题,4*8=32)
1. 下列说法正确的是( )
A.若=,则a=b B.若-x=4y,则x=-2y
C.若ax=bx,则a=b D.若a2=b2,则a=b
2. 已知线段AB,在BA的延长线上取一点C,使CA=3AB,则线段CA与线段CB的比为( )
A.3:4 B.2:3
C.3:5 D.1:2
3. 如图,正五边形FGHMN与正五边形ABCDE相似,若AB:FG=2:3,则下列结论正确的是( )
A.2DE=3MN B.3DE=2MN
C.3∠A=2∠F D.2∠A=3∠F
4. 如图,D是△ABC的边AB上一点,要使△ACD∽△ABC,则必须具备的条件可以是( )
A.= B.=
C.CD2=AD·DB D.AC2=AD·AB
5. 宽与长的比是(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD,BC的中点E,F,连接EF;以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是( )
A.矩形ABFE B.矩形EFCD
C.矩形EFGH D.矩形DCGH
6. 如图,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5 m,测得AB=1.2 m,BC=12.8 m,则建筑物CD的高是( )
A.17.5 m B.17 m
C.16.5 m D.18 m
7. 如图,点E,F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于点H,若=2,则的值为( )
A. B.
C. D.
8. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A.1.25尺 B.57.5尺
C.6.25尺 D.56.5尺
二.填空题(共6小题,4*6=24)
9.若1,2,3,x是成比例线段,则x=_________.
10. 如图,E为 ABCD的边AB延长线上的一点,且BE∶AB=2∶3,连接DE交BC于点F,则CF∶AD=__ __.
,
11. 如图,在△ABC中,DE∥AB,且=,则的值为________.
12. 主持人主持节目时,站在舞台的黄金分割点处最自然得体.如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她至少走__________米才最理想.
13. 如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆,小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为__ __米.
14. 如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且=,若点A(-1,0),点C(,1),则A′C′=_______.
三.解答题(共5小题, 44分)
15.(6分) 如图,在△ABC中,AD是中线,且CD2=BE·BA.求证:ED·AB=AD·BD.
16.(8分) 如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场上的旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶端A在同一直线上.已知DE=0.5 m,EF=0.25 m,目测点D到地面的距离DG=1.5 m,到旗杆的水平距离DC=20 m ,求旗杆的高度.
17.(8分) )如图,在四边形ABCD中,AB∥CD,连接BD,AB=8,BD=12,CD=18.
(1)求证:△ABD∽△BDC;
(2)若△ABD的面积为40,求四边形ABCD的面积.
18.(10分) 如图,已知△ABC,∠BAC的平分线与△ABC的外角∠DAC的平分线分别交BC及BC的延长线于点P,Q.
(1)求∠PAQ的度数;
(2)若点M为PQ的中点,连接AM,求证:PM2=CM·BM.
19.(12分) 如图,在矩形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.
(1)如图①,当=时,求的值;
(2)如图②,当=时,求AF与OA的比值(用含m的代数式表示);
(3)如图③,当=时,过点F作FG⊥BC于点G,探索EG与BG的数量关系(用含m的代数式表示),并说明理由.
参考答案
1-4AABD 5-8DABB
9.6
10.3∶5
11.
12.18-6
13.22.5
14.
15.证明:∵AD是中线,∴BD=CD.又CD2=BE·BA,∴BD2=BE·BA,即=,又∠B=∠B,∴△BED∽△BDA,∴=,∴ED·AB=AD·BD.
16.解:∵∠DEF=∠DCA=90°,∠EDF=∠CDA,∴△DEF∽△DCA.∴=.∵DE=0.5 m,EF=0.25 m,DC=20 m,∴=.∴AC=10 m.又∵CB=DG=1.5 m,∴AB=AC+CB=10+1.5=11.5(m).答:旗杆的高度为11.5 m.
17.解:(1)证明:∵AB∥CD,∴∠ABD=∠BDC.∵AB=8,BD=12,CD=18,∴==,∴△ABD∽△BDC
(2)∵△ABD∽△BDC,=,∴=()2=.又∵△ABD的面积为40,∴S△BDC=90,∴四边形ABCD的面积为40+90=130
18.解:∵AP平分∠BAC,∴∠PAC=∠BAC.∵AQ平分∠CAD,∴∠CAQ=∠CAD.
∴∠PAC+∠CAQ=∠BAC+∠CAD=(∠BAC+∠CAD).又∵∠BAC+∠CAD=180°,∴∠PAC+∠CAQ=90°,即∠PAQ=90°.
(2)证明:由(1)知∠PAQ=90°.∵M是PQ的中点,∴PM=AM.∴∠APM=∠PAM.∵∠APM=∠B+∠BAP,∠PAM=∠CAM+∠PAC,∠BAP=∠PAC,∴∠CAM=∠B.又∵∠AMC=∠BMA,∴△ACM∽△BAM. ∴=.∴AM2=CM·BM,即PM2=CM·BM.
19.解:(1)∵=,∴=,∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∴△CEF∽△ADF,∴=,∴==,==
(2)设EC=1,则BE=m,∵四边形ABCD是矩形,∴AD∥BC,AD=BC=m+1,∴△CEF∽△ADF,∴==,∴=,∵=,∴AC=2OA,∴=,∴=
(3)结论:=()2,理由:设EC=1,则BE=m,∵四边形ABCD是矩形,∴AD∥BC,AD=BC=m+1,∴△CEF∽△ADF,∴===,∵FG⊥BC,∴FG∥CD,∴==,①∵FG∥AB,∴==,②由①×②,可得×=×,即=()2
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
