山东省济南市莱芜区实验中学片区教研共同体(五四制)2020-2022学年九年级上学期期中考试数学试题(Word版无答案)
文档属性
| 名称 | 山东省济南市莱芜区实验中学片区教研共同体(五四制)2020-2022学年九年级上学期期中考试数学试题(Word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 221.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 10:16:15 | ||
图片预览


文档简介
实验中学片区教研共同体2021—2022学年度上学期学业水平测试
初四数学试题
本试题共8页,分选择题部分和非选择题部分.选择题部分满分为36分,非选择题部分满分为84分.全卷满分为120分.考试时间为120分钟.
答题前,请考生务必将自己的姓名、座号和准考证号填写在答题卡上,并同时将姓名、准考证号和座号填写在试题规定的位置.
答题时,选择题部分每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.非选择题部分,用0.5毫米黑色签字笔在答题卡上题号所提示的答题区域作答,直接在试题上作答无效.
第I卷(共36分)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若函数的图象过点,则此函数图象位于( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
2.已知反比例函数,下列结论不正确的是 ( )
A.图象必经过点(-1,2) B.若x>1,则y>-2
C.图象在第二、四象限内 D.y随x的增大而增大
3.对于二次函数y=(x+1)2+2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线x=﹣1
C.顶点坐标是(1,2) D.与x轴有两个交点
4.如图所示,△ABC的顶点是正方形网格的格点,则的值为( )
A. B. C. D.
5.若抛物线是关于x的二次函数,那么m的值是( )
A.3 B. C.2 D.2或3
6.在中,∠C=90°,,则的值为( )
A. B. C. D.
7.若代数式有意义,则实数x的取值范围是( )
A.x≥-1 B.x>-1 C.x≥-1且x≠3 D.x>-1且x≠3
8.已知点A(-3,y1),B(2,y2),C(3,y3)在抛物线y=2x2-4x+c上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y3>y1 C.y3>y2>y1 D.y1>y3>y2
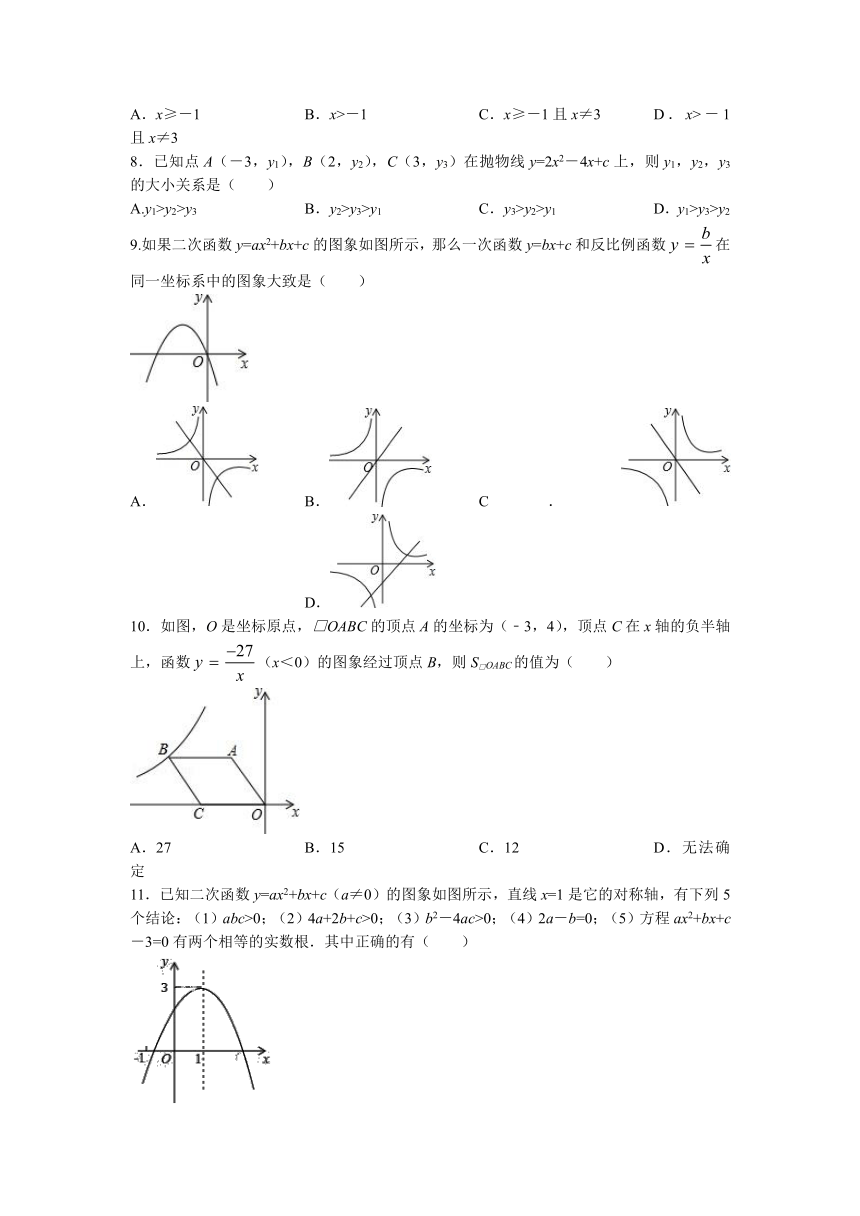
9.如果二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数在同一坐标系中的图象大致是( )
A. B. C. D.
10.如图,O是坐标原点,□OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数(x<0)的图象经过顶点B,则S□OABC的值为( )
A.27 B.15 C.12 D.无法确定
11.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,直线x=1是它的对称轴,有下列5个结论:(1)abc>0;(2)4a+2b+c>0;(3)b2-4ac>0;(4)2a-b=0;(5)方程ax2+bx+c-3=0有两个相等的实数根.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
12.如图,点A、C在反比例函数的图像上,点B、D在反比例函数的图像上,,轴,AB、CD在x轴的两侧,,,AB、CD的距离为6,则的值为( )
A.3 B. C.-3 D.无法确定
非选择题部分 (共84分)
二、填空题(本大题共6个小题,每小题3分,共18分.请直接填写答案.)
13.在△ABC中,∠A,∠B都是锐角,且,,则∠C=________;
14.如图抛物线y=ax2与反比例函数交于点C(1,2),不等式的解集是_________.
15.若函数是关于x的二次函数,且抛物线的开口向上,则m的值为______.
16.如图,正方形ABCD的顶点A、D分别在x轴、y轴上,∠ADO=30°,OA=2,反比例函数经过CD的中点M,那么k=______.
17.如图所示,点A是反比侧函数图象上一点.过点A作AB⊥x轴于点B.若OA=5,则△AOB的周长为______.
18.如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数(x>0)的图象上,则经过点B的反比例函数解析式为______.
三、解答题(本大题共7小题,共66分.解答应写出文字说明、证明过程或演算步骤.)
19.计算(1)
(2)
20.如图,小亮在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为60°,此时他距地面的高度AE为21米,电梯再上升9米到达D点,此时测得大楼BC楼顶B点的仰角为45°,求大楼BC的高度.(结果保留根号)
21.如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:,,,】
22.在平面直角坐标系中,二次函数的顶点为A(1,—4),且经过点B(3,0)
(1)求这个二次函数表达式;
(2)将这个二次函数图像向右平移几个单位,可使平移后所得图像经过坐标原点;
(3)直接写出平移后所得图像与x轴的另一个交点的坐标。
23.某商场在销售某种进价为20元/件的商品时,以30元/件售出,每天销售100件。根据市场调研,若每件商品的售价上涨1元,其销售数量就减少2件。
(1)为了实现每天1600元的销售利润,商场应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,商场为了获得最大的利润,应将该商品售价定为多少?每天最大利润为多少?
24.如图,一次函数y1=ax+b与反比例函数的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围。
(3)点P是x轴上一点,当时,请求出点P的坐标.
25.如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
备用图
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为?若存在求出点Q的坐标;若不存在请说明理由.
初四数学试题
本试题共8页,分选择题部分和非选择题部分.选择题部分满分为36分,非选择题部分满分为84分.全卷满分为120分.考试时间为120分钟.
答题前,请考生务必将自己的姓名、座号和准考证号填写在答题卡上,并同时将姓名、准考证号和座号填写在试题规定的位置.
答题时,选择题部分每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.非选择题部分,用0.5毫米黑色签字笔在答题卡上题号所提示的答题区域作答,直接在试题上作答无效.
第I卷(共36分)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若函数的图象过点,则此函数图象位于( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
2.已知反比例函数,下列结论不正确的是 ( )
A.图象必经过点(-1,2) B.若x>1,则y>-2
C.图象在第二、四象限内 D.y随x的增大而增大
3.对于二次函数y=(x+1)2+2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线x=﹣1
C.顶点坐标是(1,2) D.与x轴有两个交点
4.如图所示,△ABC的顶点是正方形网格的格点,则的值为( )
A. B. C. D.
5.若抛物线是关于x的二次函数,那么m的值是( )
A.3 B. C.2 D.2或3
6.在中,∠C=90°,,则的值为( )
A. B. C. D.
7.若代数式有意义,则实数x的取值范围是( )
A.x≥-1 B.x>-1 C.x≥-1且x≠3 D.x>-1且x≠3
8.已知点A(-3,y1),B(2,y2),C(3,y3)在抛物线y=2x2-4x+c上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y3>y1 C.y3>y2>y1 D.y1>y3>y2
9.如果二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数在同一坐标系中的图象大致是( )
A. B. C. D.
10.如图,O是坐标原点,□OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数(x<0)的图象经过顶点B,则S□OABC的值为( )
A.27 B.15 C.12 D.无法确定
11.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,直线x=1是它的对称轴,有下列5个结论:(1)abc>0;(2)4a+2b+c>0;(3)b2-4ac>0;(4)2a-b=0;(5)方程ax2+bx+c-3=0有两个相等的实数根.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
12.如图,点A、C在反比例函数的图像上,点B、D在反比例函数的图像上,,轴,AB、CD在x轴的两侧,,,AB、CD的距离为6,则的值为( )
A.3 B. C.-3 D.无法确定
非选择题部分 (共84分)
二、填空题(本大题共6个小题,每小题3分,共18分.请直接填写答案.)
13.在△ABC中,∠A,∠B都是锐角,且,,则∠C=________;
14.如图抛物线y=ax2与反比例函数交于点C(1,2),不等式的解集是_________.
15.若函数是关于x的二次函数,且抛物线的开口向上,则m的值为______.
16.如图,正方形ABCD的顶点A、D分别在x轴、y轴上,∠ADO=30°,OA=2,反比例函数经过CD的中点M,那么k=______.
17.如图所示,点A是反比侧函数图象上一点.过点A作AB⊥x轴于点B.若OA=5,则△AOB的周长为______.
18.如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数(x>0)的图象上,则经过点B的反比例函数解析式为______.
三、解答题(本大题共7小题,共66分.解答应写出文字说明、证明过程或演算步骤.)
19.计算(1)
(2)
20.如图,小亮在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为60°,此时他距地面的高度AE为21米,电梯再上升9米到达D点,此时测得大楼BC楼顶B点的仰角为45°,求大楼BC的高度.(结果保留根号)
21.如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:,,,】
22.在平面直角坐标系中,二次函数的顶点为A(1,—4),且经过点B(3,0)
(1)求这个二次函数表达式;
(2)将这个二次函数图像向右平移几个单位,可使平移后所得图像经过坐标原点;
(3)直接写出平移后所得图像与x轴的另一个交点的坐标。
23.某商场在销售某种进价为20元/件的商品时,以30元/件售出,每天销售100件。根据市场调研,若每件商品的售价上涨1元,其销售数量就减少2件。
(1)为了实现每天1600元的销售利润,商场应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,商场为了获得最大的利润,应将该商品售价定为多少?每天最大利润为多少?
24.如图,一次函数y1=ax+b与反比例函数的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围。
(3)点P是x轴上一点,当时,请求出点P的坐标.
25.如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
备用图
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为?若存在求出点Q的坐标;若不存在请说明理由.
同课章节目录
