鲁教版(五四制)七年级下册数学第七章 二元一次方程组 达标检测卷(Word版 含答案)
文档属性
| 名称 | 鲁教版(五四制)七年级下册数学第七章 二元一次方程组 达标检测卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 283.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 10:27:31 | ||
图片预览



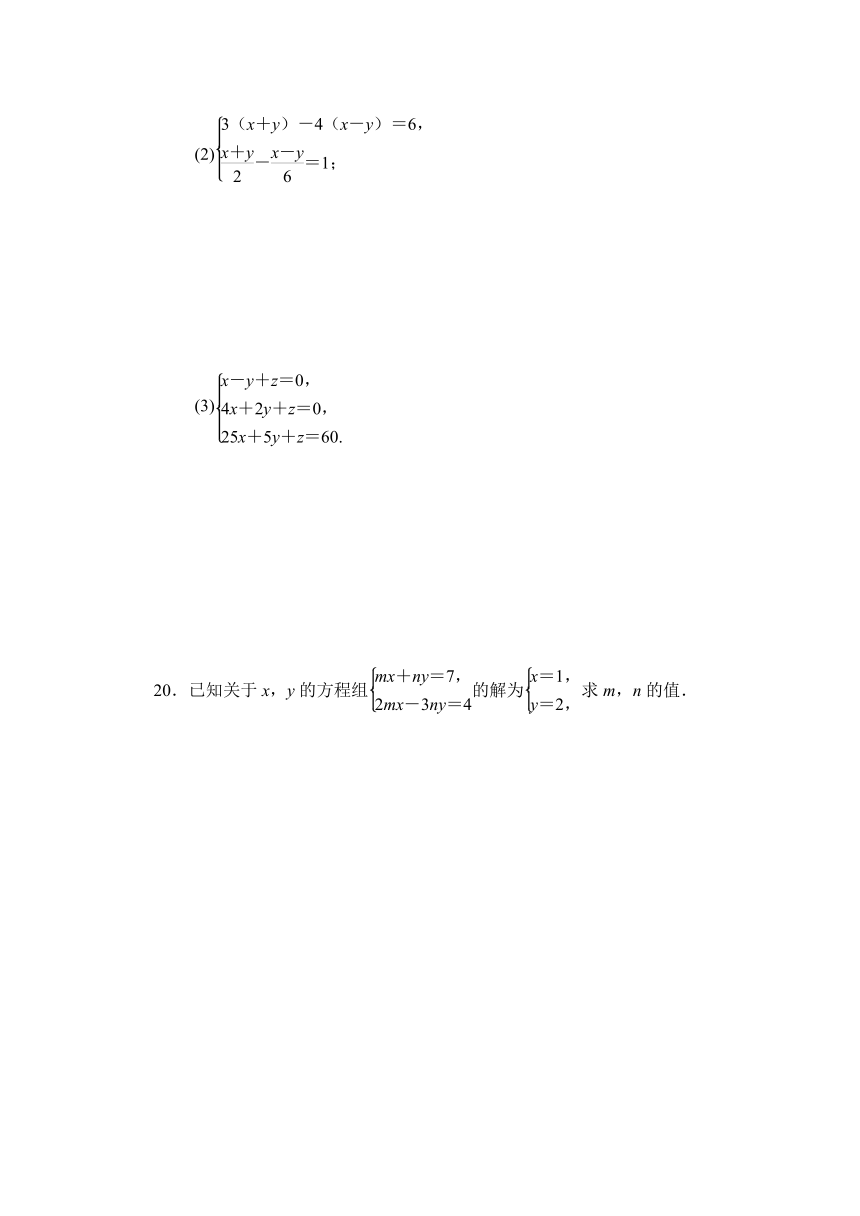

文档简介
第七章达标检测卷
一、选择题(每题3分,共30分)
1.下列方程中,是二元一次方程的是( )
A.2x+1=0 B.3x+y=2z
C.xy=9 D.3x-2y=5
2.下列方程组①②③④⑤中,是二元一次方程组的有( )
A.1个 B.2个 C.3个 D.4个
3.用代入法解方程组下面的变形正确的是( )
A.2y-3y+3=1 B.2y-3y-3=1
C.2y-3y+1=1 D.2y-3y-1=1
4.关于x,y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值是( )
A.- B. C. D.-
5.以的解为坐标的点(x,y)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.在函数y=kx+b中,当x=3时,y=-4;当x=4时,y=-3,则k,b的值分别为( )
A.1,-7 B.7,-1 C.-1,7 D.-7,1
7.若方程x+2y=-4,2x-y=7,y-kx+9=0有公共解,则k的值是( )
A.-3 B.3 C.6 D.-6
8.如图所示的两台天平保持平衡,已知每块巧克力的质量相等,且每个果冻的质量也相等,则每块巧克力和每个果冻的质量分别为( )
A.10 g,40 g B.15 g,35 g
C.20 g,30 g D.30 g,20 g
9.学校计划购买A和B两种品牌的足球,已知一个A品牌足球60元,一个B品牌足球75元.学校准备将1 500元钱全部用于购买这两种足球(两种足球都买),该学校的购买方案共有( )
A.3种 B.4种 C.5种 D.6种
10.某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快递,乙仓库用来派发快递,该时段内甲、乙两仓库的快递数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递数量相同时,此刻的时间为( )
A.9:15 B.9:20 C.9:25 D.9:30
二、填空题(每题3分,共24分)
11.已知(n-1)x|n|-2ym-2 022=0是关于x,y的二元一次方程,则nm=________.
12.某班级学生准备分组开展学雷锋活动,若每组7人,则余2人;若每组8人,又缺5人.设这个班级的学生数为x,分成的组数为y,则可得到方程组为________________.
13.若是关于x,y的二元一次方程组的解,则n的值为________.
14.若关于x,y的二元一次方程组的解满足x-y=1,则k的值是________.
15.定义运算“*”,规定x*y=ax2+by,其中a,b为常数,且1*2=5,
2*1=6,则2*3=________.
16.一个三位数的各位数字之和等于14,个位数字与十位数字的和比百位数字大2,如果把百位数字与十位数字对调,所得新数比原数小270,则原三位数为________.
17.如图①,在边长为a的大正方形中剪去一个边长为b的小正方形,再将剩下的部分沿虚线剪拼成一个长方形,如图②所示,拼成的这个长方形的长为30,宽为20,则图②中Ⅱ部分的面积是________.
18.在一次越野赛中,当小明跑了1 600 m时,小刚跑了1 400 m,小明、小刚在此后所跑的路程y(m)与时间t(s)之间的函数关系如图所示,则这次越野赛的全程为__________.
三、解答题(19题9分,20,21题每题10分,22,23题每题12分,24题13分,共66分)
19.解方程组:
(1)
(2)
(3)
20.已知关于x,y的方程组的解为求m,n的值.
21.小明和小刚同时解方程组
根据小明和小刚的对话(如图),试求a,b,c的值.
22.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=x-1交于点D,C为直线CD与y轴的交点.求:
(1)直线AB对应的函数表达式;
(2)S△ADC.
23.如图,某工厂与A,B两地由公路、铁路相连.这家工厂从A地购买一批每吨2 000元的原料运回工厂,制成每吨7 500元的产品运到B地.已知公路运价为2元/(吨·千米),铁路运价为1.5元/(吨·千米),且这两次运输共支出公路运输费2.6万元,铁路运输费15.6万元.
(1)该工厂从A地购买了多少吨原料?制成运往B地的产品为多少吨?
(2)若不计人力成本,这批产品盈利多少元?(盈利=销售额-原料费-运
输费)
24.为奖励在演讲比赛中获奖的同学,班主任派学习委员小明为获奖同学买奖品,要求每人一件.小明到文具店看了商品后,决定奖品在钢笔和笔记本中选择.如果买4本笔记本和2支钢笔,则需86元;如果买3本笔记本和1支钢笔,则需57元.
(1)求购买每本笔记本和每支钢笔分别需要多少元;
(2)售货员提示,买钢笔有优惠,具体方法:如果买钢笔超过10支,那么
超出部分可以享受八折优惠,若买x(x>0)支钢笔需要y1元,请你求出y1关于x的函数表达式;
(3)在(2)的条件下,小明决定买同一种奖品,数量超过10件,请帮小明判
断买哪种奖品省钱.
答案
一、1.D 2.B 3.A 4.B 5.A 6.A 7.B 8.C 9.B 10.B
二、11.-1
12.
13.5
14.0 点拨:
①-②得x-y=3k+1,代入x-y=1中得3k+1=1,解得k=0.
15.10
16.635 点拨:设原三位数的个位、十位、百位上的数字分别为x,y,z,则
解得 故原三位数为635.
17.100
18.2 200 m
三、 19.解:(1)
①+②,得3x=9,
解得x=3.
把x=3代入①,得y=-1.
所以原方程组的解为
(2)
②×6,得3(x+y)-(x-y)=6,③
①-③,得-3(x-y)=0,
即x=y.
将x=y代入③,得3(y+y)-0=6,
即y=1.
所以x=1.
所以原方程组的解为
(3)
②-①,得3x+3y=0,即x=-y,
③-①,得24x+6y=60,
即4x+y=10,④
将x=-y代入④,得-4y+y=10,
即y=-.所以x=.
将y=-,x=代入①,得z=-.
所以原方程组的解为
20.解:将代入方程组得
解得
所以m,n的值分别为5,1.
21.解:把分别代入方程组的第1个方程中,
得
解得
再把代入方程cx+y=6中,
得4c+(-2)=6,
所以c=2.
故a=5,b=-3,c=2.
22.解:(1)设直线AB对应的函数表达式为y=kx+b,把A(0,2),B(3,0)的坐标分别代入,得
解得
所以直线AB对应的函数表达式为y=-x+2.
(2)当x=0时,y=x-1=-1,则点C的坐标为(0,-1).解方程组
得
则点D的坐标为.
所以S△ADC=×(2+1)×2=3.
23.解:(1)设该工厂从A地购买了x吨原料,制成运往B地的产品为y吨,依题意得,
整理,得
解得
答:该工厂从A地购买了500吨原料,制成运往B地的产品为400吨.
(2)产品销售额为400×7 500=3 000 000(元),
原料费为500×2 000=1 000 000(元),
运费为26 000+156 000=182 000(元),
3 000 000-1 000 000-182 000=1 818 000(元).
答:这批产品盈利1 818 000元.
24.解:(1)设购买每本笔记本需要m元,每支钢笔需要n元.
则依题意可列方程组
解得
所以购买每本笔记本需要14元,购买每支钢笔需要15元.
(2)当0<x≤10时,y1=15x;
当x>10时,y1=10×15+80%×15(x-10)=12x+30.
所以y1=
(3)设买x本笔记本需要y2元,则y2=14x.
当x>10时,y2-y1=14x-(12x+30)=2x-30.
当2x-30=0时,x=15.
当10<x<15时,y2<y1;
当x=15时,y2=y1;
当x>15时,y2>y1.
综上所述,当买奖品超过10件但少于15件时,买笔记本省钱;当买15件奖品时,买笔记本和钢笔的钱数一样;当买奖品超过15件时,买钢笔省钱.
一、选择题(每题3分,共30分)
1.下列方程中,是二元一次方程的是( )
A.2x+1=0 B.3x+y=2z
C.xy=9 D.3x-2y=5
2.下列方程组①②③④⑤中,是二元一次方程组的有( )
A.1个 B.2个 C.3个 D.4个
3.用代入法解方程组下面的变形正确的是( )
A.2y-3y+3=1 B.2y-3y-3=1
C.2y-3y+1=1 D.2y-3y-1=1
4.关于x,y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值是( )
A.- B. C. D.-
5.以的解为坐标的点(x,y)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.在函数y=kx+b中,当x=3时,y=-4;当x=4时,y=-3,则k,b的值分别为( )
A.1,-7 B.7,-1 C.-1,7 D.-7,1
7.若方程x+2y=-4,2x-y=7,y-kx+9=0有公共解,则k的值是( )
A.-3 B.3 C.6 D.-6
8.如图所示的两台天平保持平衡,已知每块巧克力的质量相等,且每个果冻的质量也相等,则每块巧克力和每个果冻的质量分别为( )
A.10 g,40 g B.15 g,35 g
C.20 g,30 g D.30 g,20 g
9.学校计划购买A和B两种品牌的足球,已知一个A品牌足球60元,一个B品牌足球75元.学校准备将1 500元钱全部用于购买这两种足球(两种足球都买),该学校的购买方案共有( )
A.3种 B.4种 C.5种 D.6种
10.某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快递,乙仓库用来派发快递,该时段内甲、乙两仓库的快递数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递数量相同时,此刻的时间为( )
A.9:15 B.9:20 C.9:25 D.9:30
二、填空题(每题3分,共24分)
11.已知(n-1)x|n|-2ym-2 022=0是关于x,y的二元一次方程,则nm=________.
12.某班级学生准备分组开展学雷锋活动,若每组7人,则余2人;若每组8人,又缺5人.设这个班级的学生数为x,分成的组数为y,则可得到方程组为________________.
13.若是关于x,y的二元一次方程组的解,则n的值为________.
14.若关于x,y的二元一次方程组的解满足x-y=1,则k的值是________.
15.定义运算“*”,规定x*y=ax2+by,其中a,b为常数,且1*2=5,
2*1=6,则2*3=________.
16.一个三位数的各位数字之和等于14,个位数字与十位数字的和比百位数字大2,如果把百位数字与十位数字对调,所得新数比原数小270,则原三位数为________.
17.如图①,在边长为a的大正方形中剪去一个边长为b的小正方形,再将剩下的部分沿虚线剪拼成一个长方形,如图②所示,拼成的这个长方形的长为30,宽为20,则图②中Ⅱ部分的面积是________.
18.在一次越野赛中,当小明跑了1 600 m时,小刚跑了1 400 m,小明、小刚在此后所跑的路程y(m)与时间t(s)之间的函数关系如图所示,则这次越野赛的全程为__________.
三、解答题(19题9分,20,21题每题10分,22,23题每题12分,24题13分,共66分)
19.解方程组:
(1)
(2)
(3)
20.已知关于x,y的方程组的解为求m,n的值.
21.小明和小刚同时解方程组
根据小明和小刚的对话(如图),试求a,b,c的值.
22.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=x-1交于点D,C为直线CD与y轴的交点.求:
(1)直线AB对应的函数表达式;
(2)S△ADC.
23.如图,某工厂与A,B两地由公路、铁路相连.这家工厂从A地购买一批每吨2 000元的原料运回工厂,制成每吨7 500元的产品运到B地.已知公路运价为2元/(吨·千米),铁路运价为1.5元/(吨·千米),且这两次运输共支出公路运输费2.6万元,铁路运输费15.6万元.
(1)该工厂从A地购买了多少吨原料?制成运往B地的产品为多少吨?
(2)若不计人力成本,这批产品盈利多少元?(盈利=销售额-原料费-运
输费)
24.为奖励在演讲比赛中获奖的同学,班主任派学习委员小明为获奖同学买奖品,要求每人一件.小明到文具店看了商品后,决定奖品在钢笔和笔记本中选择.如果买4本笔记本和2支钢笔,则需86元;如果买3本笔记本和1支钢笔,则需57元.
(1)求购买每本笔记本和每支钢笔分别需要多少元;
(2)售货员提示,买钢笔有优惠,具体方法:如果买钢笔超过10支,那么
超出部分可以享受八折优惠,若买x(x>0)支钢笔需要y1元,请你求出y1关于x的函数表达式;
(3)在(2)的条件下,小明决定买同一种奖品,数量超过10件,请帮小明判
断买哪种奖品省钱.
答案
一、1.D 2.B 3.A 4.B 5.A 6.A 7.B 8.C 9.B 10.B
二、11.-1
12.
13.5
14.0 点拨:
①-②得x-y=3k+1,代入x-y=1中得3k+1=1,解得k=0.
15.10
16.635 点拨:设原三位数的个位、十位、百位上的数字分别为x,y,z,则
解得 故原三位数为635.
17.100
18.2 200 m
三、 19.解:(1)
①+②,得3x=9,
解得x=3.
把x=3代入①,得y=-1.
所以原方程组的解为
(2)
②×6,得3(x+y)-(x-y)=6,③
①-③,得-3(x-y)=0,
即x=y.
将x=y代入③,得3(y+y)-0=6,
即y=1.
所以x=1.
所以原方程组的解为
(3)
②-①,得3x+3y=0,即x=-y,
③-①,得24x+6y=60,
即4x+y=10,④
将x=-y代入④,得-4y+y=10,
即y=-.所以x=.
将y=-,x=代入①,得z=-.
所以原方程组的解为
20.解:将代入方程组得
解得
所以m,n的值分别为5,1.
21.解:把分别代入方程组的第1个方程中,
得
解得
再把代入方程cx+y=6中,
得4c+(-2)=6,
所以c=2.
故a=5,b=-3,c=2.
22.解:(1)设直线AB对应的函数表达式为y=kx+b,把A(0,2),B(3,0)的坐标分别代入,得
解得
所以直线AB对应的函数表达式为y=-x+2.
(2)当x=0时,y=x-1=-1,则点C的坐标为(0,-1).解方程组
得
则点D的坐标为.
所以S△ADC=×(2+1)×2=3.
23.解:(1)设该工厂从A地购买了x吨原料,制成运往B地的产品为y吨,依题意得,
整理,得
解得
答:该工厂从A地购买了500吨原料,制成运往B地的产品为400吨.
(2)产品销售额为400×7 500=3 000 000(元),
原料费为500×2 000=1 000 000(元),
运费为26 000+156 000=182 000(元),
3 000 000-1 000 000-182 000=1 818 000(元).
答:这批产品盈利1 818 000元.
24.解:(1)设购买每本笔记本需要m元,每支钢笔需要n元.
则依题意可列方程组
解得
所以购买每本笔记本需要14元,购买每支钢笔需要15元.
(2)当0<x≤10时,y1=15x;
当x>10时,y1=10×15+80%×15(x-10)=12x+30.
所以y1=
(3)设买x本笔记本需要y2元,则y2=14x.
当x>10时,y2-y1=14x-(12x+30)=2x-30.
当2x-30=0时,x=15.
当10<x<15时,y2<y1;
当x=15时,y2=y1;
当x>15时,y2>y1.
综上所述,当买奖品超过10件但少于15件时,买笔记本省钱;当买15件奖品时,买笔记本和钢笔的钱数一样;当买奖品超过15件时,买钢笔省钱.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
