鲁教版(五四制)七年级下册数学第八章 平行线的有关证明 达标检测卷(Word版 含答案)
文档属性
| 名称 | 鲁教版(五四制)七年级下册数学第八章 平行线的有关证明 达标检测卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 466.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 10:28:18 | ||
图片预览




文档简介
第八章达标检测卷
一、选择题(每题3分,共30分)
1.“两条直线相交成直角,就称这两条直线互相垂直”这个句子是( )
A.定义 B.结论 C.基本事实 D.定理
2.如果a∥b,b∥c,那么a∥c,这个推理的依据是( )
A.等量代换
B.同位角相等,两直线平行
C.垂直于同一条直线的两条直线平行
D.平行于同一条直线的两条直线平行
3.如图,AB∥CD,FE⊥DB,垂足为点E,∠1=50°,则∠2的度数是( )
A.60° B.50° C.40° D.30°
4.命题:①对顶角相等;②同角的补角相等;③相等的角是对顶角;④内错角相等.其中假命题是( )
A.①② B.①③ C.②④ D.③④
5.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.两直线平行,同位角相等
B.同旁内角互补,两直线平行
C.内错角相等,两直线平行
D.同位角相等,两直线平行
6.如图,在下列条件中,不能判定直线a与b平行的是( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠5 D.∠3+∠4=180°
7.如图,已知△ABC中,点D在AC上,连接BD,延长BC至点E,连接DE,则下列结论不成立的是( )
A.∠DCE>∠ADB B.∠ADB>∠DBC
C.∠ADB>∠ACB D.∠ADB>∠DEC
8.如图,∠1+∠2+∠3+∠4=( )
A.360° B.180° C.280° D.320°
9.如图,已知∠1=120°,∠2=60°,∠3+∠4=180°,则在结论①a∥b;②a∥c;③b∥c;④∠3=∠2中,正确的个数是( )
A.1个 B.2个 C.3个 D.4个
10.如图,点P是△ABC三条角平分线的交点,若∠BPC=108°,则下列结论中正确的是( )
A.∠BAC=54° B.∠BAC=36°
C.∠ABC+∠ACB=108° D.∠ABC+∠ACB=72°
二、填空题(每题3分,共24分)
11.把命题“对顶角相等”改写成“如果……那么……”的形式为__________________________________________.
12.请举反例说明命题 “对于任意实数x,x2+5x+5的值总是整数”是假命题,你举的反例是x=________.(写出一个x的值即可)
13.如图,DF平分∠CDE,∠CDF=50°,∠C=80°,则________∥________.
14.如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F.若∠1=42°,则∠2=________.
15.对于同一平面内的三条直线,给出下列5个论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c.以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题.
已知:________;结论:________;理由: ________________________.
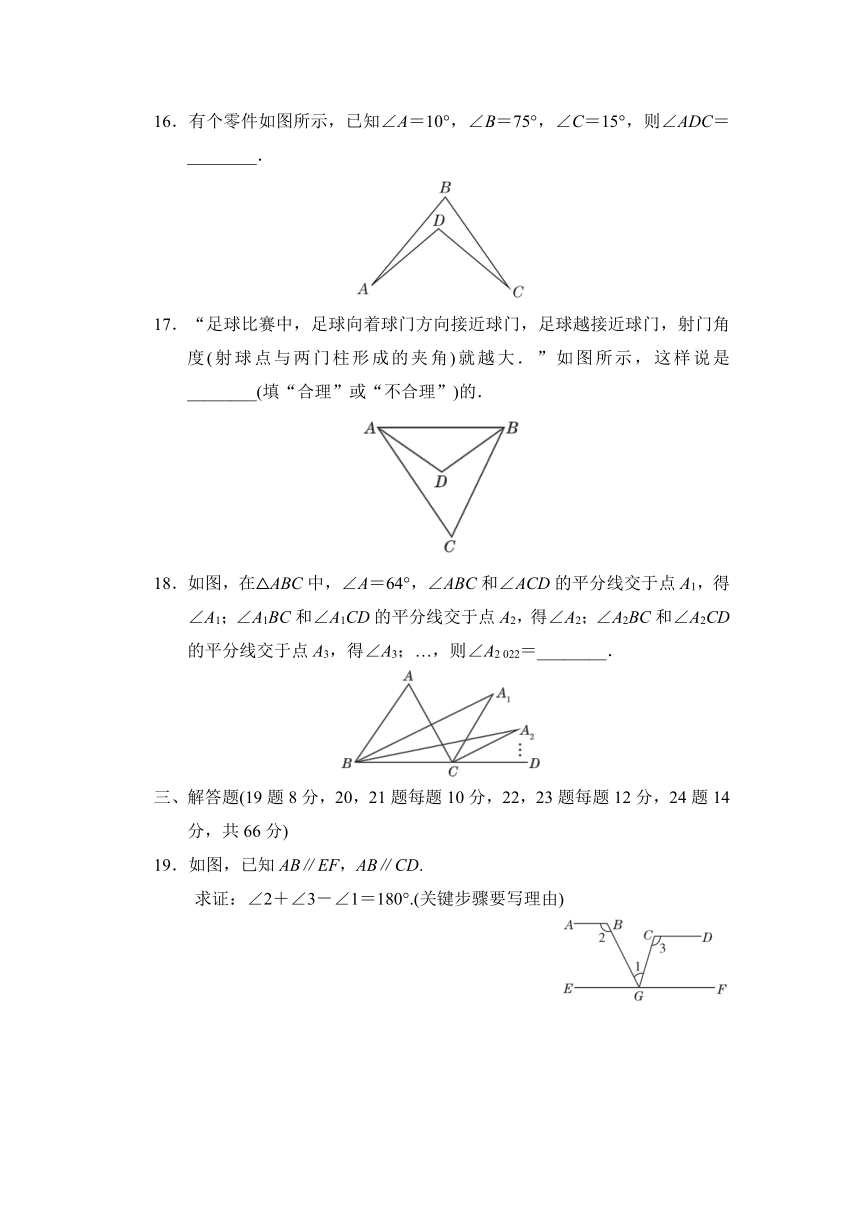
16.有个零件如图所示,已知∠A=10°,∠B=75°,∠C=15°,则∠ADC=________.
17.“足球比赛中,足球向着球门方向接近球门,足球越接近球门,射门角度(射球点与两门柱形成的夹角)就越大.”如图所示,这样说是________(填“合理”或“不合理”)的.
18.如图,在△ABC中,∠A=64°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;∠A2BC和∠A2CD的平分线交于点A3,得∠A3;…,则∠A2 022=________.
三、解答题(19题8分,20,21题每题10分,22,23题每题12分,24题14分,共66分)
19.如图,已知AB∥EF,AB∥CD.
求证:∠2+∠3-∠1=180°.(关键步骤要写理由)
20.阅读理解:
如果一个三角形满足一个内角α是另一个内角β的3倍时,那么我们称这个三角形为“智慧三角形”.其中α称为“智慧角”.
解答问题:
一个内角为60°的直角三角形______(填“是”或“不是”)“智慧三角形”;
若是,“智慧角”是______.
已知一个“智慧三角形”的“智慧角”为108°,求这个“智慧三角形”各个
内角的度数.
21.判断下列命题的真假,若为假命题,请举出反例;若为真命题,请给予证明.
(1)若一次函数y=kx+b的图象不经过第二象限,则k>0,b<0;
(2)等腰三角形底边上的中点到两腰的距离相等.
22.如图,在四边形ABCD中,AB∥CD,点E,F分别在AD,BC边上,连接AC交EF于G,连接AF,已知∠1=∠BAC.
(1)求证:EF∥CD;
(2)若∠CAF=15°,∠2=45°,∠3=20°,求∠B和∠ACD的度数.
23.如图,把一张长方形纸片ABCD沿EF折叠后,点D,C分别落在点D′,C′的位置,ED′与BC的交点为G,若∠EFG=55°,求∠1,∠2的度数.
24.小明在学习三角形知识时,发现如下三个有趣的结论:在直角三角形ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为点E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD,MF的位置关系是________;
如图②,M为边AC反向延长线上一点,则BD,MF的位置关系是________;
如图③,M为边AC的延长线上一点,则BD,MF的位置关系是________.
(2)请就图①、图②或图③中的任意一种情况给出证明,我选图________来证明.
答案
一、1.A 2.D 3.C 4.D 5.D 6.C 7.A 8.C 9.C 10.B
二、11.如果两个角是对顶角,那么这两个角相等
12.(答案不唯一) 13.CB;DE 14.159°
15.①②;④;平行于同一条直线的两直线平行(答案不唯一)
16.100°
17.合理
18.° 点拨:∵BA1平分∠ABC,CA1平分∠ACD,
∴∠A1BC=∠ABC,∠A1CD=∠ACD.
∵∠A1CD=∠A1+∠A1BC,
即∠ACD=∠A1+∠ABC,
∴∠A1=(∠ACD-∠ABC).
∵∠A+∠ABC=∠ACD,
∴∠A=∠ACD-∠ABC,
∴∠A1=∠A.
同理可得∠A2=∠A1=∠A,…,
以此类推∠A2 022=∠A==°.
三、 19.证明:∵AB∥EF,AB∥CD(已知),
∴EF∥CD(平行于同一条直线的两条直线平行),
∴∠3=∠CGE(两直线平行,内错角相等),
∴∠3-∠1=∠CGE-∠1=∠BGE(等式的性质).
∵AB∥EG(已知),
∴∠2+∠BGE=180°(两直线平行,同旁内角互补),
∴∠2+∠3-∠1=180°(等量代换).
20.解:(1)是;90°
(2)∵一个“智慧三角形”的“智慧角”为108°,
∴这个三角形的另一个内角为108°÷3=36°.
又∵180°-108°-36°=36°,
∴这个“智慧三角形”的三个内角的度数分别为36°,36°,108°.
21.解:(1)是假命题.反例:当k>0,b=0时,一次函数y=kx+b的图象也不经过第二象限.
(2)是真命题.
已知:如图,AB=AC,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.
证明:∵AB=AC,
∴∠B=∠C.
又∵BD=CD,∠BED=∠CFD=90°,
∴△BED≌△CFD.
∴DE=DF.
22.(1)证明:∵∠1=∠BAC,
∴AB∥EF.
∵AB∥CD,
∴EF∥CD.
(2)解:由(1)知AB∥EF,
∴∠B+∠BFE=180°.
∵∠BFE=∠2+∠3=65°,
∴∠B=115°.
∵∠1是△AGF的外角,
∴∠1=∠3+∠GAF=35°.
由(1)知EF∥CD,
∴∠ACD=∠1=35°.
23.解:∵AD∥BC,
∴∠FED=∠EFG=55°,
∠2+∠1=180°.
由折叠的性质得∠FED=∠FEG,
∴∠1=180°-∠FED-∠FEG=180°-2∠FED=70°.
∴∠2=180°-∠1=110°.
24.解:(1)平行;垂直;垂直
(2)(答案不唯一)①
证明:∵∠A=90°,ME⊥BC,
∴∠A=∠CEM=90°,
∴∠C+∠ABC=90°,
∠C+∠CME=90°,
∴∠CME=∠ABC.
∵∠CME+∠AME=180°,
∴∠ABC+∠AME=180°.
∵BD平分∠ABC,MF平分∠AME.
∴∠ABD=∠ABC,∠AMF=∠AME.
∴∠ABD+∠AMF=(∠ABC+∠AME)=90°.
又∵∠AMF+∠AFM=90°,
∴∠AFM=∠ABD.
∴BD∥MF.
一、选择题(每题3分,共30分)
1.“两条直线相交成直角,就称这两条直线互相垂直”这个句子是( )
A.定义 B.结论 C.基本事实 D.定理
2.如果a∥b,b∥c,那么a∥c,这个推理的依据是( )
A.等量代换
B.同位角相等,两直线平行
C.垂直于同一条直线的两条直线平行
D.平行于同一条直线的两条直线平行
3.如图,AB∥CD,FE⊥DB,垂足为点E,∠1=50°,则∠2的度数是( )
A.60° B.50° C.40° D.30°
4.命题:①对顶角相等;②同角的补角相等;③相等的角是对顶角;④内错角相等.其中假命题是( )
A.①② B.①③ C.②④ D.③④
5.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.两直线平行,同位角相等
B.同旁内角互补,两直线平行
C.内错角相等,两直线平行
D.同位角相等,两直线平行
6.如图,在下列条件中,不能判定直线a与b平行的是( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠5 D.∠3+∠4=180°
7.如图,已知△ABC中,点D在AC上,连接BD,延长BC至点E,连接DE,则下列结论不成立的是( )
A.∠DCE>∠ADB B.∠ADB>∠DBC
C.∠ADB>∠ACB D.∠ADB>∠DEC
8.如图,∠1+∠2+∠3+∠4=( )
A.360° B.180° C.280° D.320°
9.如图,已知∠1=120°,∠2=60°,∠3+∠4=180°,则在结论①a∥b;②a∥c;③b∥c;④∠3=∠2中,正确的个数是( )
A.1个 B.2个 C.3个 D.4个
10.如图,点P是△ABC三条角平分线的交点,若∠BPC=108°,则下列结论中正确的是( )
A.∠BAC=54° B.∠BAC=36°
C.∠ABC+∠ACB=108° D.∠ABC+∠ACB=72°
二、填空题(每题3分,共24分)
11.把命题“对顶角相等”改写成“如果……那么……”的形式为__________________________________________.
12.请举反例说明命题 “对于任意实数x,x2+5x+5的值总是整数”是假命题,你举的反例是x=________.(写出一个x的值即可)
13.如图,DF平分∠CDE,∠CDF=50°,∠C=80°,则________∥________.
14.如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F.若∠1=42°,则∠2=________.
15.对于同一平面内的三条直线,给出下列5个论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c.以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题.
已知:________;结论:________;理由: ________________________.
16.有个零件如图所示,已知∠A=10°,∠B=75°,∠C=15°,则∠ADC=________.
17.“足球比赛中,足球向着球门方向接近球门,足球越接近球门,射门角度(射球点与两门柱形成的夹角)就越大.”如图所示,这样说是________(填“合理”或“不合理”)的.
18.如图,在△ABC中,∠A=64°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;∠A2BC和∠A2CD的平分线交于点A3,得∠A3;…,则∠A2 022=________.
三、解答题(19题8分,20,21题每题10分,22,23题每题12分,24题14分,共66分)
19.如图,已知AB∥EF,AB∥CD.
求证:∠2+∠3-∠1=180°.(关键步骤要写理由)
20.阅读理解:
如果一个三角形满足一个内角α是另一个内角β的3倍时,那么我们称这个三角形为“智慧三角形”.其中α称为“智慧角”.
解答问题:
一个内角为60°的直角三角形______(填“是”或“不是”)“智慧三角形”;
若是,“智慧角”是______.
已知一个“智慧三角形”的“智慧角”为108°,求这个“智慧三角形”各个
内角的度数.
21.判断下列命题的真假,若为假命题,请举出反例;若为真命题,请给予证明.
(1)若一次函数y=kx+b的图象不经过第二象限,则k>0,b<0;
(2)等腰三角形底边上的中点到两腰的距离相等.
22.如图,在四边形ABCD中,AB∥CD,点E,F分别在AD,BC边上,连接AC交EF于G,连接AF,已知∠1=∠BAC.
(1)求证:EF∥CD;
(2)若∠CAF=15°,∠2=45°,∠3=20°,求∠B和∠ACD的度数.
23.如图,把一张长方形纸片ABCD沿EF折叠后,点D,C分别落在点D′,C′的位置,ED′与BC的交点为G,若∠EFG=55°,求∠1,∠2的度数.
24.小明在学习三角形知识时,发现如下三个有趣的结论:在直角三角形ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为点E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD,MF的位置关系是________;
如图②,M为边AC反向延长线上一点,则BD,MF的位置关系是________;
如图③,M为边AC的延长线上一点,则BD,MF的位置关系是________.
(2)请就图①、图②或图③中的任意一种情况给出证明,我选图________来证明.
答案
一、1.A 2.D 3.C 4.D 5.D 6.C 7.A 8.C 9.C 10.B
二、11.如果两个角是对顶角,那么这两个角相等
12.(答案不唯一) 13.CB;DE 14.159°
15.①②;④;平行于同一条直线的两直线平行(答案不唯一)
16.100°
17.合理
18.° 点拨:∵BA1平分∠ABC,CA1平分∠ACD,
∴∠A1BC=∠ABC,∠A1CD=∠ACD.
∵∠A1CD=∠A1+∠A1BC,
即∠ACD=∠A1+∠ABC,
∴∠A1=(∠ACD-∠ABC).
∵∠A+∠ABC=∠ACD,
∴∠A=∠ACD-∠ABC,
∴∠A1=∠A.
同理可得∠A2=∠A1=∠A,…,
以此类推∠A2 022=∠A==°.
三、 19.证明:∵AB∥EF,AB∥CD(已知),
∴EF∥CD(平行于同一条直线的两条直线平行),
∴∠3=∠CGE(两直线平行,内错角相等),
∴∠3-∠1=∠CGE-∠1=∠BGE(等式的性质).
∵AB∥EG(已知),
∴∠2+∠BGE=180°(两直线平行,同旁内角互补),
∴∠2+∠3-∠1=180°(等量代换).
20.解:(1)是;90°
(2)∵一个“智慧三角形”的“智慧角”为108°,
∴这个三角形的另一个内角为108°÷3=36°.
又∵180°-108°-36°=36°,
∴这个“智慧三角形”的三个内角的度数分别为36°,36°,108°.
21.解:(1)是假命题.反例:当k>0,b=0时,一次函数y=kx+b的图象也不经过第二象限.
(2)是真命题.
已知:如图,AB=AC,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.
证明:∵AB=AC,
∴∠B=∠C.
又∵BD=CD,∠BED=∠CFD=90°,
∴△BED≌△CFD.
∴DE=DF.
22.(1)证明:∵∠1=∠BAC,
∴AB∥EF.
∵AB∥CD,
∴EF∥CD.
(2)解:由(1)知AB∥EF,
∴∠B+∠BFE=180°.
∵∠BFE=∠2+∠3=65°,
∴∠B=115°.
∵∠1是△AGF的外角,
∴∠1=∠3+∠GAF=35°.
由(1)知EF∥CD,
∴∠ACD=∠1=35°.
23.解:∵AD∥BC,
∴∠FED=∠EFG=55°,
∠2+∠1=180°.
由折叠的性质得∠FED=∠FEG,
∴∠1=180°-∠FED-∠FEG=180°-2∠FED=70°.
∴∠2=180°-∠1=110°.
24.解:(1)平行;垂直;垂直
(2)(答案不唯一)①
证明:∵∠A=90°,ME⊥BC,
∴∠A=∠CEM=90°,
∴∠C+∠ABC=90°,
∠C+∠CME=90°,
∴∠CME=∠ABC.
∵∠CME+∠AME=180°,
∴∠ABC+∠AME=180°.
∵BD平分∠ABC,MF平分∠AME.
∴∠ABD=∠ABC,∠AMF=∠AME.
∴∠ABD+∠AMF=(∠ABC+∠AME)=90°.
又∵∠AMF+∠AFM=90°,
∴∠AFM=∠ABD.
∴BD∥MF.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
