2021-2022学年数学人教A版(2019)选择性必修第一册3.1 椭圆 课后尖子生培优练(Word含答案解析)
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)选择性必修第一册3.1 椭圆 课后尖子生培优练(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 745.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 17:08:36 | ||
图片预览




文档简介
3.1椭圆课后尖子生培优练--2021--2022学年人教A(2019)版高二上学期第三章圆锥曲线的方程
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.椭圆的焦点坐标是( )
A., B.,
C., D.,
2.若方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是( )
A.(0,+∞) B.(0,2) C.(1,+∞) D.(0,1)
3.已知点分别是椭圆的左 右焦点,点P在此椭圆上,,则的面积等于
A. B. C. D.
4.椭圆两焦点为 ,在椭圆上,若的面积的最大值为12,则椭圆方程是( )
A. B.
C. D.
5.已知圆,从圆上任意一点向轴作垂线段,为垂足,则线段的中点的轨迹方程为( )
A. B. C. D.
6.已知椭圆C:的左 右顶点分别为,,且以线段为直径的圆与直线相切,则椭圆C的离心率为( )
A. B. C. D.
7.已知椭圆C:x21的焦点分别为F1,F2,P是椭圆C上的动点,则下列结论正确的是( )
A.|PF1|+|PF2|=2
B.△PF1F2面积的最大值是
C.椭圆C的离心率为
D.以线段F1F2为直径的圆与直线相切
8.嫦娥四号月球探测器于2018年12月8日搭载长征三号乙运载火箭在西昌卫星发射中心发射.12日下午4点43分左右,嫦娥四号顺利进入了以月球球心为一个焦点的椭圆形轨道,如图中轨道③所示,其近月点与月球表面距离为公里,远月点与月球表面距离为公里.已知月球的直径为公里,则该椭圆形轨道的离心率约为
A. B. C. D.
评卷人得分
二、多选题
9.关于椭圆,以下说法正确的是( )
A.长轴长为 B.焦距为
C.离心率为 D.左顶点的坐标为
10.已知椭圆的焦距为4,则( )
A.椭圆C的焦点在x轴上 B.椭圆C的长轴长是短轴长的倍
C.椭圆C的离心率为 D.椭圆C上的点到其一个焦点的最大距离为
11.已知是椭圆上一点,,是其左右焦点,则下列选项中正确的是( )
A.椭圆的焦距为2 B.椭圆的离心率
C. D.的面积的最大值是4
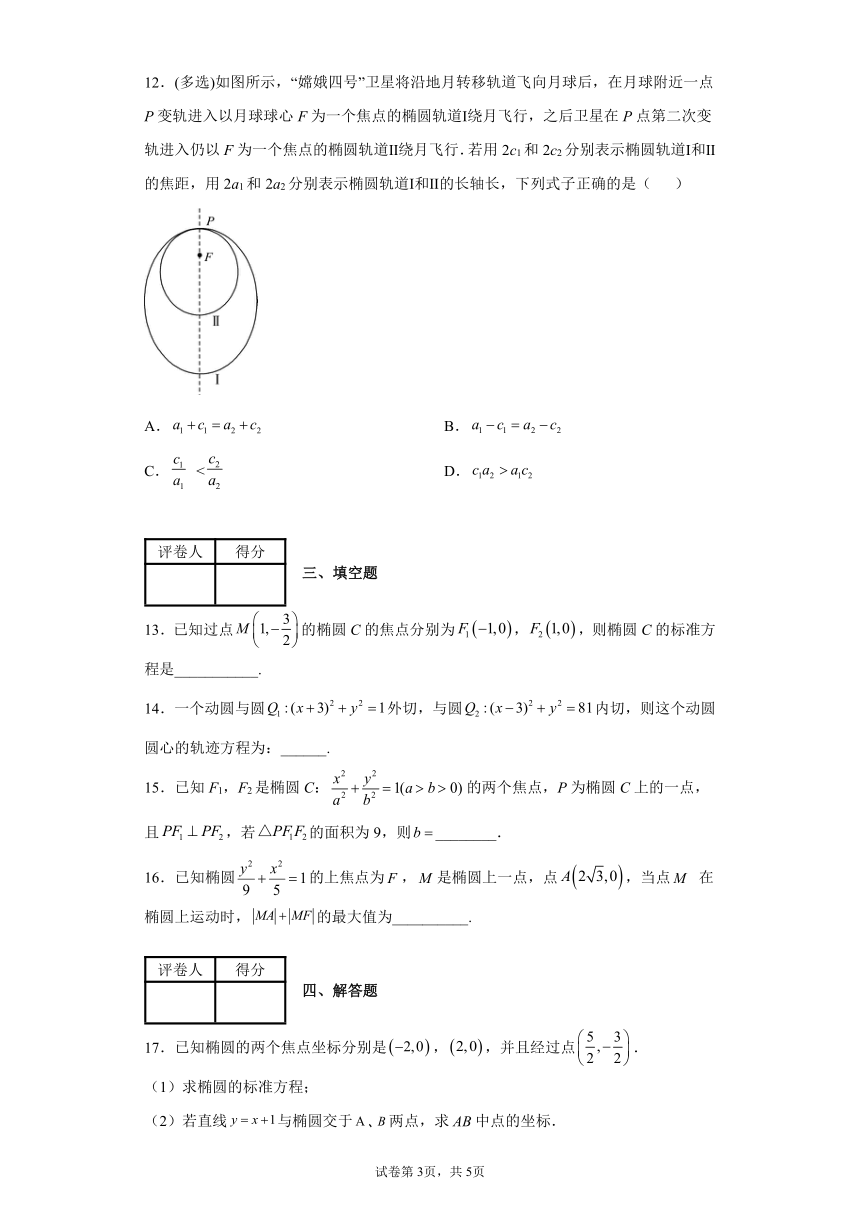
12.(多选)如图所示,“嫦娥四号”卫星将沿地月转移轨道飞向月球后,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行.若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,下列式子正确的是( )
A. B.
C. < D.
评卷人得分
三、填空题
13.已知过点的椭圆C的焦点分别为,,则椭圆C的标准方程是___________.
14.一个动圆与圆外切,与圆内切,则这个动圆圆心的轨迹方程为:______.
15.已知F1,F2是椭圆C:的两个焦点,P为椭圆C上的一点,且,若的面积为9,则________.
16.已知椭圆的上焦点为,是椭圆上一点,点,当点 在椭圆上运动时,的最大值为__________.
评卷人得分
四、解答题
17.已知椭圆的两个焦点坐标分别是,,并且经过点.
(1)求椭圆的标准方程;
(2)若直线与椭圆交于 两点,求中点的坐标.
18.在平面直角坐标系中,已知点到两点的距离之和等于,设点的轨迹为曲线.
(1)求曲线的方程.
(2)若直线与曲线有公共点,求实数的取值范围.
19.椭圆E与有共同的焦点,且经过点
(1)求椭圆E的标准方程和离心率;
(2)设F为E的左焦点,M为椭圆E上任意一点,求的最大值.
20.已知椭圆的离心率为,短轴一个端点到右焦点的距离为3.
(1)求椭圆C的方程;
(2)设直线交椭圆C于A、B两点,求线段AB的中点坐标.
21.如图,设点在轴上,且关于原点对称.点满足,且的面积为.
(Ⅰ)求点的坐标;
(Ⅱ)以为焦点,且过点的椭圆记为.设是上一点,且,求的取值范围.
22.已知焦点在轴上的椭圆:,短轴长为,椭圆左顶点到左焦点的距离为.
(1)求椭圆的标准方程;
(2)如图,已知点,点是椭圆的右顶点,直线与椭圆交于不同的两点 ,两点都在轴上方,且.证明直线过定点,并求出该定点坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
【解】根据方程可得,且焦点在x轴,
又,所以,
所以焦点坐标为,.
故选:B
2.D
【解】
因为方程,即 表示焦点在轴上的椭圆,
所以 ,即 ,
所以实数的取值范围是.
故选:D.
3.B
【解】
椭圆
则,所以,
则
由余弦定理可知
代入化简可得,
则,
故选:B.
4.B
【解】
由题意,当点在短轴端点时,的面积的最大值为12,
可得,解得,又,
故
故椭圆的方程为
故选:B
5.A
【解】
设线段的中点,,
所以,解得,
又点在圆上,
则,即.
故选:A
6.D
【解】因为椭圆C:的左 右顶点分别为,,
因此以为直径的圆的半径为,圆心坐标为,
又该圆与直线相切,
所以圆心到直线的距离等于半径,即,则,
因此,即,所以离心率为.
故选:D.
7.D
【解】由题意可知,椭圆C:x21的焦点在y轴上,长半轴长a,短半轴长,
设,,则,设,
对于选项A:|PF1|+|PF2|=,故A错误;
对于选项B:因为△PF1F2面积为,故B错误;
对于选项C:椭圆的离心率e,故C错误;
对于选项D:以线段F1F2为直径的圆的圆心为原点O(0,0),半径,
故原点O(0,0)到直线的距离,
从而以线段F1F2为直径的圆与直线x+y0相切,故D正确.
故选:D.
8.B
【解】
如下图,F为月球的球心,月球半径为:×3476=1738,
依题意,|AF|=100+1738=1838,
|BF|=400+1738=2138.
2a=1838+2138,
a=1988,
a+c=2138,
c=2138-1988=150,
椭圆的离心率为:,
选B.
9.BCD
【解】
椭圆的焦点在轴上,,.
对于A选项,该椭圆的长轴长为,A错误;
对于B选项,该椭圆的焦距为,B对;
对于C选项,该椭圆的离心率为,C对;
对于D选项,该椭圆的左顶点坐标为,D对.
故选:BCD.
10.BC
解析因为,所以,所以焦点在轴上,故A错误;
又因为焦距为,所以,所以,所以,
所以长轴长,短轴长,所以,故B正确;
因为,所以离心率,故C正确;
因为椭圆方程,取一个焦点,设椭圆上的点,
所以,
又因为,当时取最大值,所以,故D错误;
故选:BC.
11.BD
【解】,∴,,
焦距,,当M为短轴的端点时的面积的取得最大值,是,
故选:BD.
12.BD
【解】观察图形可知,即A不正确;,即B正确;
由, 知,,即,从而,即: ,即D正确,C不正确.
故选:BD
13.
【解】由题意,,所以,
所以椭圆方程为.
故答案为:.
14.
【解】设动圆的圆心为,半径为R,
因为动圆与圆外切,与圆内切,
所以,
所以,
所以动圆圆心的轨迹为以为焦点的椭圆,
所以,
所以动圆圆心的轨迹方程为,
故答案为:
15.3
【解】
设,由椭圆的定义可得,
又由,可得,
可得,即,
所以的面积为,
又因为的面积为9,即,解得.
故答案为:
16.
解:如图所示:
设椭圆的下焦点为,
,
,,
又,
即,
,
又,
当且仅当,,共线且在线段上时等号成立,
,
,
,
的最大值为.
故答案为:.
17.【解】(1)由于椭圆的焦点在轴上,所以设它的标准方程为,
由椭圆定义知,
,
所以,所以,
所求椭圆标准方程为.
(2)设直线与椭圆的交点为,,
联立方程,得,
得,.
设的中点坐标为,则,,
所以中点坐标为.
18.解:(1)由己知得
由椭圆定义可知,轨迹是以,为焦点,焦距长,长轴长的椭圆.
所以,
所以曲线的方程是.
(2)由得.
,
因为直线与曲线有公共点,
所以,即,
解得,或.
故实数的取值范围是.
19.【解】(1)由,可得,
设椭圆E的标准方程:,且经过点.
,解得,
所以椭圆E的标准方程:,
.
(2)由(1)可知:,,
设 (为参数),
则 ,,
所以
,()
当时,取得最大值,即的最大值为.
20.【解】(1)因为椭圆的离心率为,短轴一个端点到右焦点的距离为3,所以,所以
所以椭圆C的方程为
(2)设
由可得,所以
所以线段AB的中点坐标为
21.【解】(Ⅰ)如图所示:
设,
则直线的方程为,直线的方程为.
由 解得
所以.
故的面积.
所以,
解得.
所以点的坐标为.
(Ⅱ)由(Ⅰ)得.
所以, .
设以为焦点且过点的椭圆方程为.
则,又,
所以椭圆的方程为.
所以, 即.
因为,所以.
所以.
所以的取值范围是.
22.【解】
(1)由得,
所以椭圆的标准方程为.
(2)当直线斜率不存在时,直线与椭圆交于不同的两点分布在轴两侧,不合题意.
所以直线斜率存在,设直线的方程为.
设、,
由得,
所以,.
因为,
所以,
即,整理得
化简得,
所以直线的方程为,
所以直线过定点.
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.椭圆的焦点坐标是( )
A., B.,
C., D.,
2.若方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是( )
A.(0,+∞) B.(0,2) C.(1,+∞) D.(0,1)
3.已知点分别是椭圆的左 右焦点,点P在此椭圆上,,则的面积等于
A. B. C. D.
4.椭圆两焦点为 ,在椭圆上,若的面积的最大值为12,则椭圆方程是( )
A. B.
C. D.
5.已知圆,从圆上任意一点向轴作垂线段,为垂足,则线段的中点的轨迹方程为( )
A. B. C. D.
6.已知椭圆C:的左 右顶点分别为,,且以线段为直径的圆与直线相切,则椭圆C的离心率为( )
A. B. C. D.
7.已知椭圆C:x21的焦点分别为F1,F2,P是椭圆C上的动点,则下列结论正确的是( )
A.|PF1|+|PF2|=2
B.△PF1F2面积的最大值是
C.椭圆C的离心率为
D.以线段F1F2为直径的圆与直线相切
8.嫦娥四号月球探测器于2018年12月8日搭载长征三号乙运载火箭在西昌卫星发射中心发射.12日下午4点43分左右,嫦娥四号顺利进入了以月球球心为一个焦点的椭圆形轨道,如图中轨道③所示,其近月点与月球表面距离为公里,远月点与月球表面距离为公里.已知月球的直径为公里,则该椭圆形轨道的离心率约为
A. B. C. D.
评卷人得分
二、多选题
9.关于椭圆,以下说法正确的是( )
A.长轴长为 B.焦距为
C.离心率为 D.左顶点的坐标为
10.已知椭圆的焦距为4,则( )
A.椭圆C的焦点在x轴上 B.椭圆C的长轴长是短轴长的倍
C.椭圆C的离心率为 D.椭圆C上的点到其一个焦点的最大距离为
11.已知是椭圆上一点,,是其左右焦点,则下列选项中正确的是( )
A.椭圆的焦距为2 B.椭圆的离心率
C. D.的面积的最大值是4
12.(多选)如图所示,“嫦娥四号”卫星将沿地月转移轨道飞向月球后,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行.若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,下列式子正确的是( )
A. B.
C. < D.
评卷人得分
三、填空题
13.已知过点的椭圆C的焦点分别为,,则椭圆C的标准方程是___________.
14.一个动圆与圆外切,与圆内切,则这个动圆圆心的轨迹方程为:______.
15.已知F1,F2是椭圆C:的两个焦点,P为椭圆C上的一点,且,若的面积为9,则________.
16.已知椭圆的上焦点为,是椭圆上一点,点,当点 在椭圆上运动时,的最大值为__________.
评卷人得分
四、解答题
17.已知椭圆的两个焦点坐标分别是,,并且经过点.
(1)求椭圆的标准方程;
(2)若直线与椭圆交于 两点,求中点的坐标.
18.在平面直角坐标系中,已知点到两点的距离之和等于,设点的轨迹为曲线.
(1)求曲线的方程.
(2)若直线与曲线有公共点,求实数的取值范围.
19.椭圆E与有共同的焦点,且经过点
(1)求椭圆E的标准方程和离心率;
(2)设F为E的左焦点,M为椭圆E上任意一点,求的最大值.
20.已知椭圆的离心率为,短轴一个端点到右焦点的距离为3.
(1)求椭圆C的方程;
(2)设直线交椭圆C于A、B两点,求线段AB的中点坐标.
21.如图,设点在轴上,且关于原点对称.点满足,且的面积为.
(Ⅰ)求点的坐标;
(Ⅱ)以为焦点,且过点的椭圆记为.设是上一点,且,求的取值范围.
22.已知焦点在轴上的椭圆:,短轴长为,椭圆左顶点到左焦点的距离为.
(1)求椭圆的标准方程;
(2)如图,已知点,点是椭圆的右顶点,直线与椭圆交于不同的两点 ,两点都在轴上方,且.证明直线过定点,并求出该定点坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
【解】根据方程可得,且焦点在x轴,
又,所以,
所以焦点坐标为,.
故选:B
2.D
【解】
因为方程,即 表示焦点在轴上的椭圆,
所以 ,即 ,
所以实数的取值范围是.
故选:D.
3.B
【解】
椭圆
则,所以,
则
由余弦定理可知
代入化简可得,
则,
故选:B.
4.B
【解】
由题意,当点在短轴端点时,的面积的最大值为12,
可得,解得,又,
故
故椭圆的方程为
故选:B
5.A
【解】
设线段的中点,,
所以,解得,
又点在圆上,
则,即.
故选:A
6.D
【解】因为椭圆C:的左 右顶点分别为,,
因此以为直径的圆的半径为,圆心坐标为,
又该圆与直线相切,
所以圆心到直线的距离等于半径,即,则,
因此,即,所以离心率为.
故选:D.
7.D
【解】由题意可知,椭圆C:x21的焦点在y轴上,长半轴长a,短半轴长,
设,,则,设,
对于选项A:|PF1|+|PF2|=,故A错误;
对于选项B:因为△PF1F2面积为,故B错误;
对于选项C:椭圆的离心率e,故C错误;
对于选项D:以线段F1F2为直径的圆的圆心为原点O(0,0),半径,
故原点O(0,0)到直线的距离,
从而以线段F1F2为直径的圆与直线x+y0相切,故D正确.
故选:D.
8.B
【解】
如下图,F为月球的球心,月球半径为:×3476=1738,
依题意,|AF|=100+1738=1838,
|BF|=400+1738=2138.
2a=1838+2138,
a=1988,
a+c=2138,
c=2138-1988=150,
椭圆的离心率为:,
选B.
9.BCD
【解】
椭圆的焦点在轴上,,.
对于A选项,该椭圆的长轴长为,A错误;
对于B选项,该椭圆的焦距为,B对;
对于C选项,该椭圆的离心率为,C对;
对于D选项,该椭圆的左顶点坐标为,D对.
故选:BCD.
10.BC
解析因为,所以,所以焦点在轴上,故A错误;
又因为焦距为,所以,所以,所以,
所以长轴长,短轴长,所以,故B正确;
因为,所以离心率,故C正确;
因为椭圆方程,取一个焦点,设椭圆上的点,
所以,
又因为,当时取最大值,所以,故D错误;
故选:BC.
11.BD
【解】,∴,,
焦距,,当M为短轴的端点时的面积的取得最大值,是,
故选:BD.
12.BD
【解】观察图形可知,即A不正确;,即B正确;
由, 知,,即,从而,即: ,即D正确,C不正确.
故选:BD
13.
【解】由题意,,所以,
所以椭圆方程为.
故答案为:.
14.
【解】设动圆的圆心为,半径为R,
因为动圆与圆外切,与圆内切,
所以,
所以,
所以动圆圆心的轨迹为以为焦点的椭圆,
所以,
所以动圆圆心的轨迹方程为,
故答案为:
15.3
【解】
设,由椭圆的定义可得,
又由,可得,
可得,即,
所以的面积为,
又因为的面积为9,即,解得.
故答案为:
16.
解:如图所示:
设椭圆的下焦点为,
,
,,
又,
即,
,
又,
当且仅当,,共线且在线段上时等号成立,
,
,
,
的最大值为.
故答案为:.
17.【解】(1)由于椭圆的焦点在轴上,所以设它的标准方程为,
由椭圆定义知,
,
所以,所以,
所求椭圆标准方程为.
(2)设直线与椭圆的交点为,,
联立方程,得,
得,.
设的中点坐标为,则,,
所以中点坐标为.
18.解:(1)由己知得
由椭圆定义可知,轨迹是以,为焦点,焦距长,长轴长的椭圆.
所以,
所以曲线的方程是.
(2)由得.
,
因为直线与曲线有公共点,
所以,即,
解得,或.
故实数的取值范围是.
19.【解】(1)由,可得,
设椭圆E的标准方程:,且经过点.
,解得,
所以椭圆E的标准方程:,
.
(2)由(1)可知:,,
设 (为参数),
则 ,,
所以
,()
当时,取得最大值,即的最大值为.
20.【解】(1)因为椭圆的离心率为,短轴一个端点到右焦点的距离为3,所以,所以
所以椭圆C的方程为
(2)设
由可得,所以
所以线段AB的中点坐标为
21.【解】(Ⅰ)如图所示:
设,
则直线的方程为,直线的方程为.
由 解得
所以.
故的面积.
所以,
解得.
所以点的坐标为.
(Ⅱ)由(Ⅰ)得.
所以, .
设以为焦点且过点的椭圆方程为.
则,又,
所以椭圆的方程为.
所以, 即.
因为,所以.
所以.
所以的取值范围是.
22.【解】
(1)由得,
所以椭圆的标准方程为.
(2)当直线斜率不存在时,直线与椭圆交于不同的两点分布在轴两侧,不合题意.
所以直线斜率存在,设直线的方程为.
设、,
由得,
所以,.
因为,
所以,
即,整理得
化简得,
所以直线的方程为,
所以直线过定点.
