第三章 位置与坐标 章节复习检测题 2021-2022学年北师大版八年级数学上册(Word版含答案)
文档属性
| 名称 | 第三章 位置与坐标 章节复习检测题 2021-2022学年北师大版八年级数学上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 229.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 10:41:11 | ||
图片预览



文档简介
第三章 位置与坐标
100分
一、选择题(2分×14=28分)
1.在平面直角坐标系中,点A(2,-3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.点P(3,-5)到x轴、y轴的距离分别是( )
A.3、5 B.3、-5 C.5、3 D.-5、3
3.如果p(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(-2,0) B.(0,-2) C.(1,0) D.(0,1)
4.一个矩形,长为6,宽为4,若以该矩形的两条对称轴为坐标轴建立平面直角坐标系,下面哪个点不在矩形上( )
A.(3,-2) B.(-3,3) C.(-3,2) D.(0,-2)
5.已知点M到x轴的距离为1,到y轴的距离为2,则M点的坐标为( )
A.(1,2) B.(-1,-2)
C.(1,-2) D.(2,1)、(2,-1)、(-2,1)、(-2,-1)
6.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是( )
A.(2011,0) B.(2011,1) C.(2011,2) D.(2010,0)
7.如图,在平面直角坐标系中,点A(1,1)、B(-1,1)、C(-1,-2)、D(1,-2) ,按A→B→C→D→A…排列,则第2018个点所在的坐标是( )
A.(1,1) B.(-1,1) C.(-1,-2) D.(1,-2)
8.已知点A(a,1)与点B(-4,b)关于原点对称,则a+b的值为( )
A.5 B.-5 C.3 D.-3
9.在平面直角坐标系中,点P(m-3,4-2m)不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.在平面直角坐标系xOy中,线段AB的两个端点的坐标分别为A(-1,-1)、B(1,2).平移线段AB,得到线段A′B′,若点A的对应点为A′(3,-1),则点B的对应点B′的坐标是( )
A.(4,2) B.(5,2) C.(6,2) D.(5,3)
11.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )
A.(-2,1) B.(-1,1) C.(1,-2) D.(-1,-2)
12.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )
A.(4,0) B.(1,0) C.(-2,0) D.(2,0)
13. 在平面直角坐标系中,点A、B关于y轴对称,点A的坐标是(2,-8),则点B的坐标是( )
A.(-2,-8) B.(2,8) C.(-2,8) D.(8,2)
14.一个正方形在平面直角坐标系中三个顶点的坐标为(-2,-3)、(-2,1)、(2,1),则第四个顶点的坐标为( )
A.(2,2) B.(3,2) C.(2,-3) D.(2,3)
二、填空题(4分×6=24分)
15.按规律排列一列数对(1,2)、(4,5)、(9,10)…第5个有序数对是 .
16. 在平面直角坐标系中,把点A(2,3)向左移一个单位得到A′,则点A′的坐标为 .
17. 已知点A(-2,1)、B(-6,0),若白棋A飞挂后,黑棋C尖顶,黑棋C的坐标为 .
18.如图,在直角坐标系中,△OBC的顶点O(0,0)、B(-6,0),且∠OCB=90°,OC=BC,则点C关于y轴对称的点C′的坐标是 .
19.已知线段AB=3,AB∥x轴,若点A的坐标为(-1,2),则点B的坐标是 .
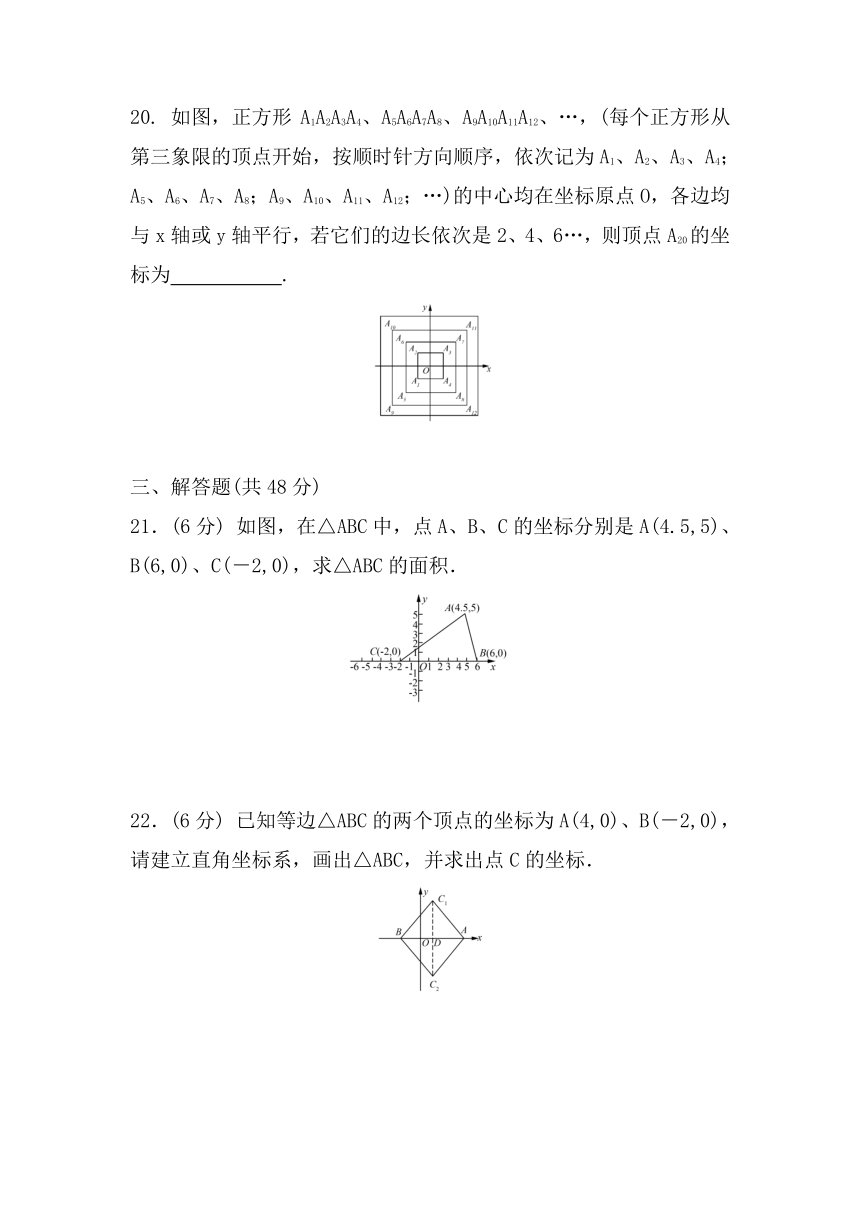
20. 如图,正方形A1A2A3A4、A5A6A7A8、A9A10A11A12、…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1、A2、A3、A4;A5、A6、A7、A8;A9、A10、A11、A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2、4、6…,则顶点A20的坐标为 .
三、解答题(共48分)
21.(6分) 如图,在△ABC中,点A、B、C的坐标分别是A(4.5,5)、B(6,0)、C(-2,0),求△ABC的面积.
22.(6分) 已知等边△ABC的两个顶点的坐标为A(4,0)、B(-2,0),请建立直角坐标系,画出△ABC,并求出点C的坐标.
23. (6分) 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,求第2017秒时,点P的坐标.
24.(9分)已知点A(a-1,-2)、B(-3,b+1).根据以下要求确定a、b的值:
(1)直线AB ∥ x轴;
(2)直线AB ∥ y轴;
(3)A、B两点在第二、四象限的角平分线上.
25.(10分)坐标平面内有4个点A(0,2)、
B(-1,0)、C(1,-1)、D(3,1).
(1)建立坐标系,描出这4个点;
(2)顺次连接A、B、C、D,组成四边形ABCD,求四边形ABCD的面积.
26.(11分)先阅读下列一段文字,再回答问题.
已知在平面内两点的坐标分别为P1(x1,y1)、P2(x2,y2),则该两点间的距离公式为P1P2=.
同时,当两点在同一坐标轴上或所在直线平行于x轴或垂直于x轴时,两点间距离公式可以化简为|x2-x1|或|y2-y1|.
(1)若已知两点A(3,5)、B(-2,-1),试求A、B两点间的距离;
(2)已知一个三角形各顶点坐标为A(0,6)、B(-3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.
答案:
一、
1-14 DCBBD CBCAB BBAC
二、
15. (25,26)
16. (1,3)
17. (-1,1)
18. (3,3)
19. (-4,2)或(2,2)
20. (5,-5)
三、
21. 解:BC=|6-(-2)|=8.作AD⊥BC于D,高AD=5,所以S△ABC=BC·AD=×8×5=20.
22. 解:如图,作C1D⊥x轴于点D,则AB=4-(-2)=6,AD=BD=3,C1D=3,∴C1点的坐标为(1,3),C2点的坐标为(1,-3).
23. 解:半圆的周长为π,点P每秒走半圆,P1(1,1)、P2(2,0)、P3(3,-1)、P4(4,0)、P5(5,1)、P6(6,0)…按此变化规律第2017秒点P坐标(2017,1).
24. 解:(1)∵直线AB ∥ x轴,∴点A与点B的纵坐标相同,∴b+1=-2,∴b=-3;
(2)∵直线AB ∥ y轴,∴点A与点B的横坐标相同,∴a-1=-3,∴a=-2;
(3)∵A、B两点在第二、四象限的角平分线上,∴a-1+(-2)=0,b+1+(-3)=0,∴a=3,b=2.
25. 解:(1)坐标系及4个点的位置,如图所示;
(2)如图,用矩形EFGH围住四边形ABCD,则S四边形ABCD=S矩形EFGH-S△ABE-S△BCF-S△CDG-S△ADH=3×4-×1×2-×1×2-×2×2-×1×3=.
26. 解:(1)AB==;
(2)能.因为:AB==5,BC==6,AC==5,所以AB=AC,即△ABC为等腰三角形.
100分
一、选择题(2分×14=28分)
1.在平面直角坐标系中,点A(2,-3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.点P(3,-5)到x轴、y轴的距离分别是( )
A.3、5 B.3、-5 C.5、3 D.-5、3
3.如果p(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(-2,0) B.(0,-2) C.(1,0) D.(0,1)
4.一个矩形,长为6,宽为4,若以该矩形的两条对称轴为坐标轴建立平面直角坐标系,下面哪个点不在矩形上( )
A.(3,-2) B.(-3,3) C.(-3,2) D.(0,-2)
5.已知点M到x轴的距离为1,到y轴的距离为2,则M点的坐标为( )
A.(1,2) B.(-1,-2)
C.(1,-2) D.(2,1)、(2,-1)、(-2,1)、(-2,-1)
6.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是( )
A.(2011,0) B.(2011,1) C.(2011,2) D.(2010,0)
7.如图,在平面直角坐标系中,点A(1,1)、B(-1,1)、C(-1,-2)、D(1,-2) ,按A→B→C→D→A…排列,则第2018个点所在的坐标是( )
A.(1,1) B.(-1,1) C.(-1,-2) D.(1,-2)
8.已知点A(a,1)与点B(-4,b)关于原点对称,则a+b的值为( )
A.5 B.-5 C.3 D.-3
9.在平面直角坐标系中,点P(m-3,4-2m)不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.在平面直角坐标系xOy中,线段AB的两个端点的坐标分别为A(-1,-1)、B(1,2).平移线段AB,得到线段A′B′,若点A的对应点为A′(3,-1),则点B的对应点B′的坐标是( )
A.(4,2) B.(5,2) C.(6,2) D.(5,3)
11.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )
A.(-2,1) B.(-1,1) C.(1,-2) D.(-1,-2)
12.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )
A.(4,0) B.(1,0) C.(-2,0) D.(2,0)
13. 在平面直角坐标系中,点A、B关于y轴对称,点A的坐标是(2,-8),则点B的坐标是( )
A.(-2,-8) B.(2,8) C.(-2,8) D.(8,2)
14.一个正方形在平面直角坐标系中三个顶点的坐标为(-2,-3)、(-2,1)、(2,1),则第四个顶点的坐标为( )
A.(2,2) B.(3,2) C.(2,-3) D.(2,3)
二、填空题(4分×6=24分)
15.按规律排列一列数对(1,2)、(4,5)、(9,10)…第5个有序数对是 .
16. 在平面直角坐标系中,把点A(2,3)向左移一个单位得到A′,则点A′的坐标为 .
17. 已知点A(-2,1)、B(-6,0),若白棋A飞挂后,黑棋C尖顶,黑棋C的坐标为 .
18.如图,在直角坐标系中,△OBC的顶点O(0,0)、B(-6,0),且∠OCB=90°,OC=BC,则点C关于y轴对称的点C′的坐标是 .
19.已知线段AB=3,AB∥x轴,若点A的坐标为(-1,2),则点B的坐标是 .
20. 如图,正方形A1A2A3A4、A5A6A7A8、A9A10A11A12、…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1、A2、A3、A4;A5、A6、A7、A8;A9、A10、A11、A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2、4、6…,则顶点A20的坐标为 .
三、解答题(共48分)
21.(6分) 如图,在△ABC中,点A、B、C的坐标分别是A(4.5,5)、B(6,0)、C(-2,0),求△ABC的面积.
22.(6分) 已知等边△ABC的两个顶点的坐标为A(4,0)、B(-2,0),请建立直角坐标系,画出△ABC,并求出点C的坐标.
23. (6分) 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,求第2017秒时,点P的坐标.
24.(9分)已知点A(a-1,-2)、B(-3,b+1).根据以下要求确定a、b的值:
(1)直线AB ∥ x轴;
(2)直线AB ∥ y轴;
(3)A、B两点在第二、四象限的角平分线上.
25.(10分)坐标平面内有4个点A(0,2)、
B(-1,0)、C(1,-1)、D(3,1).
(1)建立坐标系,描出这4个点;
(2)顺次连接A、B、C、D,组成四边形ABCD,求四边形ABCD的面积.
26.(11分)先阅读下列一段文字,再回答问题.
已知在平面内两点的坐标分别为P1(x1,y1)、P2(x2,y2),则该两点间的距离公式为P1P2=.
同时,当两点在同一坐标轴上或所在直线平行于x轴或垂直于x轴时,两点间距离公式可以化简为|x2-x1|或|y2-y1|.
(1)若已知两点A(3,5)、B(-2,-1),试求A、B两点间的距离;
(2)已知一个三角形各顶点坐标为A(0,6)、B(-3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.
答案:
一、
1-14 DCBBD CBCAB BBAC
二、
15. (25,26)
16. (1,3)
17. (-1,1)
18. (3,3)
19. (-4,2)或(2,2)
20. (5,-5)
三、
21. 解:BC=|6-(-2)|=8.作AD⊥BC于D,高AD=5,所以S△ABC=BC·AD=×8×5=20.
22. 解:如图,作C1D⊥x轴于点D,则AB=4-(-2)=6,AD=BD=3,C1D=3,∴C1点的坐标为(1,3),C2点的坐标为(1,-3).
23. 解:半圆的周长为π,点P每秒走半圆,P1(1,1)、P2(2,0)、P3(3,-1)、P4(4,0)、P5(5,1)、P6(6,0)…按此变化规律第2017秒点P坐标(2017,1).
24. 解:(1)∵直线AB ∥ x轴,∴点A与点B的纵坐标相同,∴b+1=-2,∴b=-3;
(2)∵直线AB ∥ y轴,∴点A与点B的横坐标相同,∴a-1=-3,∴a=-2;
(3)∵A、B两点在第二、四象限的角平分线上,∴a-1+(-2)=0,b+1+(-3)=0,∴a=3,b=2.
25. 解:(1)坐标系及4个点的位置,如图所示;
(2)如图,用矩形EFGH围住四边形ABCD,则S四边形ABCD=S矩形EFGH-S△ABE-S△BCF-S△CDG-S△ADH=3×4-×1×2-×1×2-×2×2-×1×3=.
26. 解:(1)AB==;
(2)能.因为:AB==5,BC==6,AC==5,所以AB=AC,即△ABC为等腰三角形.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
