1.2 30°,45°,60°的三角函数值 课件(共20张PPT)
文档属性
| 名称 | 1.2 30°,45°,60°的三角函数值 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:56:23 | ||
图片预览




文档简介
(共20张PPT)
§1.2 30°,45°,60°
的三角函数值
北师版九年级下册 直角三角形的三边关系
学习目标
1.经历探索30°,45°,60°角的三角函数值的过程,提升思维水平,进一步熟记其值.(难点)
2.学会含有30°,45°,60°角的三角函数值的简单计算.(重点)
3.能根据30°,45°,60°角的三角函数值,解决一些简单问题.(重点)
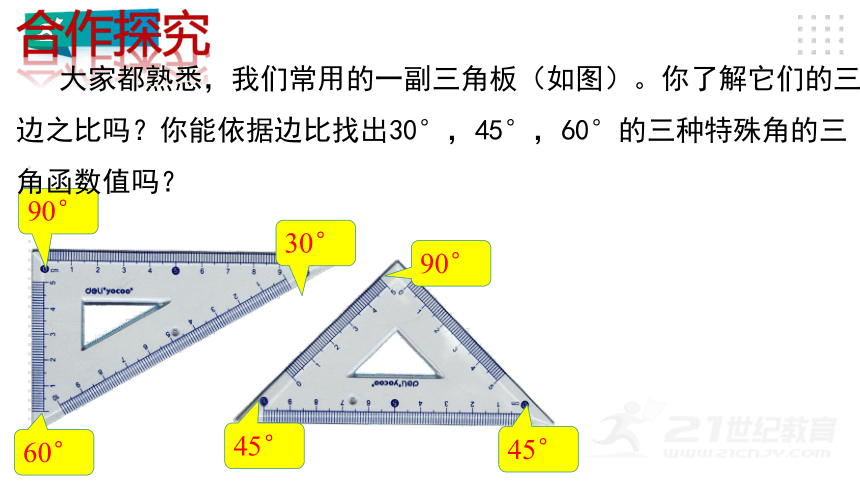
cos A=
1.正弦、余弦、正切、的定义
A
c
b
a
C
B
对边
邻边
斜边
┓
在△ABC中,∠C为直角.
∠A的对边
斜边
a
c
∠A的邻边
斜边
b
c
sin A=
tanA=
∠A的对边
∠A的邻边
=
a
b
=
=
知识回顾
45°
45°
60°
90°
90°
30°
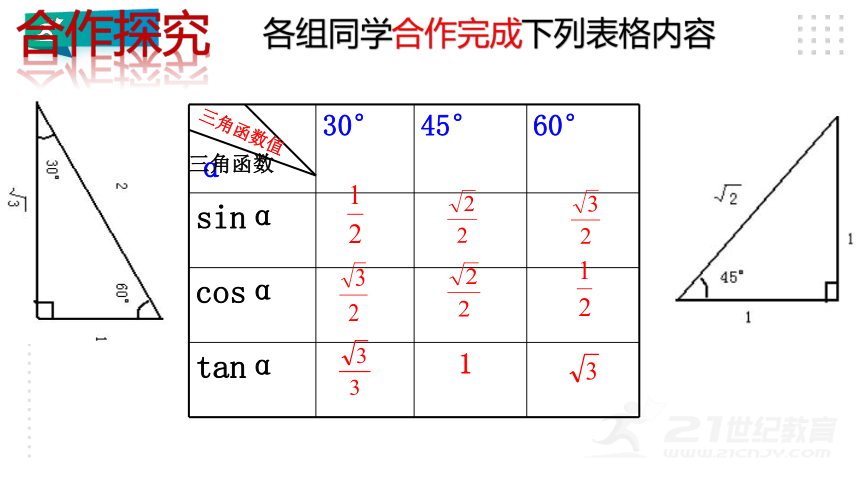
合作探究
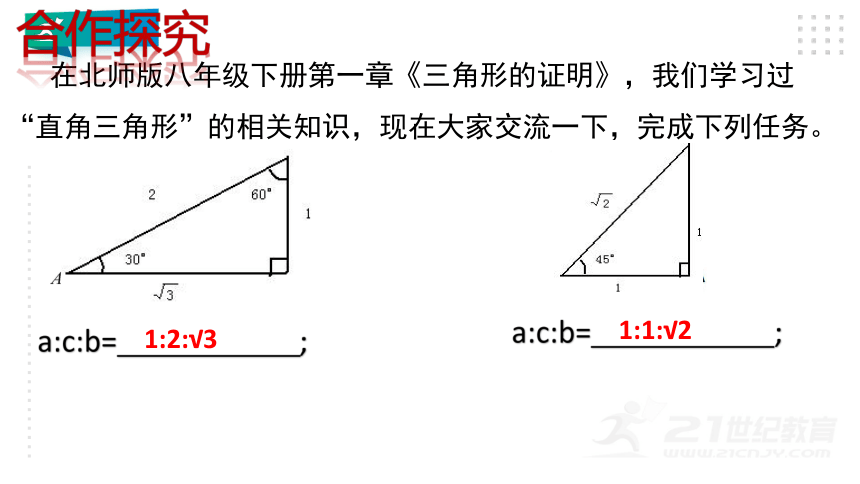
大家都熟悉,我们常用的一副三角板(如图)。你了解它们的三边之比吗?你能依据边比找出30°,45°,60°的三种特殊角的三角函数值吗?
在北师版八年级下册第一章《三角形的证明》,我们学习过
“直角三角形”的相关知识,现在大家交流一下,完成下列任务。
合作探究
a:c:b= ;
1:2:√3
a:c:b= ;
1:1:√2
合作探究
各组同学合作完成下列表格内容
α 30° 45° 60°
sinα
cosα
tanα
1
三角函数
三角函数值
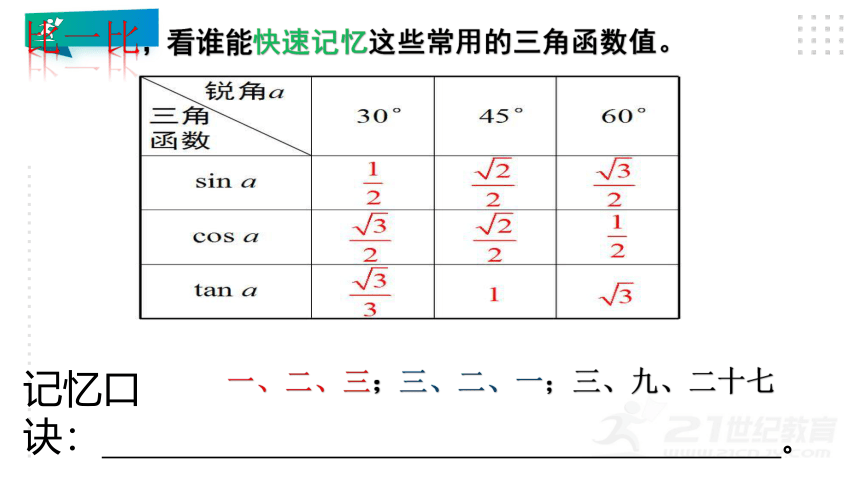
比一比,看谁能快速记忆这些常用的三角函数值。
记忆口诀: 。
一、二、三;三、二、一;三、九、二十七
【例1】计算:
(1)sin30°+cos45°;
(2)sin260°+cos260°-tan45°
特别注意:sin260°,这里表示(sin60°)2,其它情况类似。
例题精讲
一、由“角”求“值”
【例2】一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.91 m).
解∶如图1-10根据题意可知、
∠AOD=-1/2×60°=30°,OD-=2.5m,
OC=OD cos30°=2.5×√3/2≈2.165(m)
AC=2.5-2.165≈0.34(m).
所以,最高位置与最低位置的高度差约为0.34m.
例题精讲
1.计算∶
(1)sin60°-tan45°; (2)cos60°+tan45°:
(3)sin 45°+sin60°-2cos45°.
自主练习
如图,BC=7 m,∠BAC=30°,
∴AB= = = =14(m).
所以,扶梯的长度是14 m.
2.某商场有一自动扶梯、其倾斜角为30°,高为7m 扶梯的长度是多少
问题解决
3.如图,身高1.75m的小丽用一个两锐角分别为 30°和60°的三角尺测量一棵树的高度(∠A=30°),已知她与树之间的距离为5m,那么这棵树大约有多高 (结果精确到0.1m)
【例1】求满足下列条件的锐角α:
2sinα- =0
(2) tanα- 1=0
α=60°
α=30°
(3) sinA=1,则锐角A= ;
若 sin(β+15°)= ,锐角β= ,
此时cosβ= .
45°
45°
简答题
二、由“值”求“角”
例题精讲
例题精讲
【例2】(1)点M(-sin60°,cos60°), 关于x轴对称的点的坐标是( )
(2)在△ABC中,∠A、∠B都是锐角,且 , ,则
∠C= .
C
120°
D
1、如图,钓鱼竿AC长6m,露在水面上的鱼线BC长3√2m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到 AC"的位置,此时露在水面上的鱼线B'C'为3√3,则鱼竿转过的角度是( )
A.60°B.45° C.15° D. 90°
拓展提升
C
2、如图,点A、B、C均在小正方形的顶点上,且每个小正方形的边长均为1,则cos∠BAC的值为( )
拓展提升
B
解∶连接 BC,·每个小正方形的边长均为1,
AB=√5,BC=√5,AC=√10. "(√5)2+(√5)2=(√0)2,
△ABC是直角三角形,cos∠BAC=√2/2
故选∶B.
3、 在△ ABC 中,∠ A,∠ B 均为锐角,且∠ A,∠ B
满足 试判断△ ABC 的形状,并说明理由 .
拓展提升
解析:先根据条件,结合特殊角的三角函数值求出两个内角的度数,即可判断出三角形的形状 .
解:△ ABC 是直角三角形 .理由如下:
又∵∠ A , ∠ B 均为锐角,
∴∠ A=60°,∠ B=30° .
∴∠ A + ∠ B=60° +30° =90° .
∴△ ABC 是直角三角形 .
1、在Rt△ABC中,∠C=90°,各边都扩大为原来的5倍,则锐角A的三角函数值( )
A.不变 B.扩大5倍 C.缩小5倍 D.不能确定
3、计算∶tan30°sin60°+cos230°一sin245°tan45°
当堂测试
A
(2),(3),(4)
解:原式=3/4
课堂小结
30° 45° 60°
sin A
cos A
tan A
打乱顺序重新记:
1
§1.2 30°,45°,60°
的三角函数值
北师版九年级下册 直角三角形的三边关系
学习目标
1.经历探索30°,45°,60°角的三角函数值的过程,提升思维水平,进一步熟记其值.(难点)
2.学会含有30°,45°,60°角的三角函数值的简单计算.(重点)
3.能根据30°,45°,60°角的三角函数值,解决一些简单问题.(重点)
cos A=
1.正弦、余弦、正切、的定义
A
c
b
a
C
B
对边
邻边
斜边
┓
在△ABC中,∠C为直角.
∠A的对边
斜边
a
c
∠A的邻边
斜边
b
c
sin A=
tanA=
∠A的对边
∠A的邻边
=
a
b
=
=
知识回顾
45°
45°
60°
90°
90°
30°
合作探究
大家都熟悉,我们常用的一副三角板(如图)。你了解它们的三边之比吗?你能依据边比找出30°,45°,60°的三种特殊角的三角函数值吗?
在北师版八年级下册第一章《三角形的证明》,我们学习过
“直角三角形”的相关知识,现在大家交流一下,完成下列任务。
合作探究
a:c:b= ;
1:2:√3
a:c:b= ;
1:1:√2
合作探究
各组同学合作完成下列表格内容
α 30° 45° 60°
sinα
cosα
tanα
1
三角函数
三角函数值
比一比,看谁能快速记忆这些常用的三角函数值。
记忆口诀: 。
一、二、三;三、二、一;三、九、二十七
【例1】计算:
(1)sin30°+cos45°;
(2)sin260°+cos260°-tan45°
特别注意:sin260°,这里表示(sin60°)2,其它情况类似。
例题精讲
一、由“角”求“值”
【例2】一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.91 m).
解∶如图1-10根据题意可知、
∠AOD=-1/2×60°=30°,OD-=2.5m,
OC=OD cos30°=2.5×√3/2≈2.165(m)
AC=2.5-2.165≈0.34(m).
所以,最高位置与最低位置的高度差约为0.34m.
例题精讲
1.计算∶
(1)sin60°-tan45°; (2)cos60°+tan45°:
(3)sin 45°+sin60°-2cos45°.
自主练习
如图,BC=7 m,∠BAC=30°,
∴AB= = = =14(m).
所以,扶梯的长度是14 m.
2.某商场有一自动扶梯、其倾斜角为30°,高为7m 扶梯的长度是多少
问题解决
3.如图,身高1.75m的小丽用一个两锐角分别为 30°和60°的三角尺测量一棵树的高度(∠A=30°),已知她与树之间的距离为5m,那么这棵树大约有多高 (结果精确到0.1m)
【例1】求满足下列条件的锐角α:
2sinα- =0
(2) tanα- 1=0
α=60°
α=30°
(3) sinA=1,则锐角A= ;
若 sin(β+15°)= ,锐角β= ,
此时cosβ= .
45°
45°
简答题
二、由“值”求“角”
例题精讲
例题精讲
【例2】(1)点M(-sin60°,cos60°), 关于x轴对称的点的坐标是( )
(2)在△ABC中,∠A、∠B都是锐角,且 , ,则
∠C= .
C
120°
D
1、如图,钓鱼竿AC长6m,露在水面上的鱼线BC长3√2m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到 AC"的位置,此时露在水面上的鱼线B'C'为3√3,则鱼竿转过的角度是( )
A.60°B.45° C.15° D. 90°
拓展提升
C
2、如图,点A、B、C均在小正方形的顶点上,且每个小正方形的边长均为1,则cos∠BAC的值为( )
拓展提升
B
解∶连接 BC,·每个小正方形的边长均为1,
AB=√5,BC=√5,AC=√10. "(√5)2+(√5)2=(√0)2,
△ABC是直角三角形,cos∠BAC=√2/2
故选∶B.
3、 在△ ABC 中,∠ A,∠ B 均为锐角,且∠ A,∠ B
满足 试判断△ ABC 的形状,并说明理由 .
拓展提升
解析:先根据条件,结合特殊角的三角函数值求出两个内角的度数,即可判断出三角形的形状 .
解:△ ABC 是直角三角形 .理由如下:
又∵∠ A , ∠ B 均为锐角,
∴∠ A=60°,∠ B=30° .
∴∠ A + ∠ B=60° +30° =90° .
∴△ ABC 是直角三角形 .
1、在Rt△ABC中,∠C=90°,各边都扩大为原来的5倍,则锐角A的三角函数值( )
A.不变 B.扩大5倍 C.缩小5倍 D.不能确定
3、计算∶tan30°sin60°+cos230°一sin245°tan45°
当堂测试
A
(2),(3),(4)
解:原式=3/4
课堂小结
30° 45° 60°
sin A
cos A
tan A
打乱顺序重新记:
1
