1.4 解直角三角形 课件(共20张PPT)
文档属性
| 名称 | 1.4 解直角三角形 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:56:23 | ||
图片预览








文档简介
(共20张PPT)
§1.4 解直角三角形
北师版九年级下册 直角三角形的三边关系
学习目标
1.理解 解直角三角形的意义;(重点)
2.理解解直角三角形的方法并能熟练解题. (重点、难点)
3、通过本节的学习进一步提升学生综合分析、解决问题的能力。
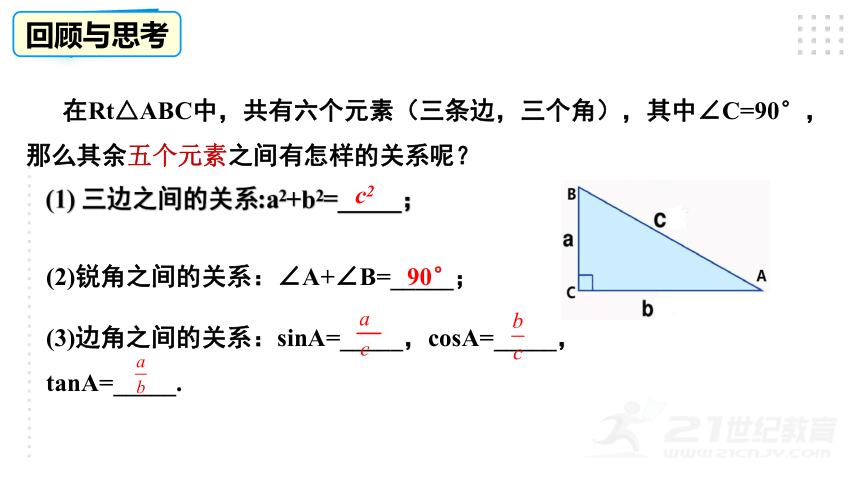
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,
tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
回顾与思考
例题精讲
【例1】 如图,在Rt△ABC中,∠C=90°, ,求这个直角三角形的其他元素.
解:在Rt△ABC中,a2+b2=c2,
∵a=√15,b=√5
∴∠B=30°
∠A=90°-30°=60°
一、知道两边长,求其它元素
像上述问题中,知道直角三角形某两个元素,求出其它元素的方法,叫做解直角三角形。
那么在Rt△ABC中,如果知道一个锐角,一条边长,你能求出其它元素吗?接下来我们继续探讨一下。
归纳小结
【例2】 如图,在Rt△ABC中,∠C=90°,b=30, ∠B=25°,求这个直角三角形的其他元素.
二、知道一个锐角,一条边长,求其它元素
例题精讲
解:在Rt△ABC中,∠C=90°,∠B=25°
∴∠A=65°
∵ sinB=b=30
∴tanB=
a==
(注意:sin25°≈0.42,tan25°≈0.47)
归纳小结
通过上述两个问题的讨论,大家慢慢会发现,在直角三角形中,只要知道一个边,和另一个元素,其它元素均可算出。
小组PK“加分赛”
在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,
根据下列条件求出直角三角形的其他元素(角度精确到1°)∶
(1)已知a=4,b=8;(提示:tan27°≈0.5)
(2)已知b=10,∠B=60°;
(3)己知c=20,∠A=60°.
解:(1)在Rt△ABC中,∠C=90°,a=4,b=8.
∴c=
∵tanA=
∴∠A≈27°,∠B≈63°.
解:(2)在Rt△ABC中,∠C=90°,∠B=60°,
∴∠A=30°.
∵ tanB= ,b=10,
∴a= .
∵ sinB= ,b=10,
∴c= .
解:(3)在Rt△ABC中,∠C=90°,∠A=60°,
∴∠B=30°.
∵ cosA= ,c=20,
∴b=10.
∵ sinA= ,c=20,
∴a= .
个人限时“加分赛”
2.在Rt△ABC'中,∠C=90°、∠A、∠B、∠C所对的边分别为a,b、c、根据下列条件求出直角二角形的其他元素∶
(1)c=20、∠A=45°: (2)a=36、∠B=30°
解:(1)∵tanA=
∴b=20,∠B=45°
∴c
(2)∵∠B=30°
∵sinA=
∴c=
∴∠A=60°
∵sinB=
∴b=
【例3】如图,在△ABC中,AC=6,BC=8,∠C=60°.求△ABC的面积。
拓展提升
解:作BD⊥AC.
∵∠C=60°,BC=8
∴CD=4,BD=4√3
∵S△ABC=1/2×AC×BD
∴S△ABC=12√3
分析:根据三角形性面积=1/2底×高,可以考虑作BC边上(或AC边上的高),利用∠C=30°,求出高即可。
变式1
在△ABC中,AC=6,BC=8,∠C= 30°. 求△ABC的面积。
变式2
在△ABC中,AC=6,BC=8,∠C= α. 求△ABC的面积。
变式3
在△ABC中,AC= b,BC= a,∠C= α. 求△ABC的面积。
解:略。
S△ABC=12
解:略。
S△ABC=12sinC
解:略。
S△ABC=1/2absinC
1、(2018·天津) cos30°的值为( )
A.√2/2 B.√3/2 C.1 D.√3
2.(2018·孝感)如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA 的值为( )
A. B. C. D.
B
A
中考链接
3.(2018·宜昌)如图,要测量小河两岸相对的两点P,A间的距离,可以在小河边取PA的垂线PB上一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于( )
A.100sin35°米 B.100sin55°米 C.100tan35°米 D.100tan55°米
C
4、(2019·长春)如图,一把梯子靠在垂直水平地面的墙上,梯子AB的长是3米.若梯子与地面的夹角为α,则梯子顶端到地面的距离 BC为( )
A.3sina米 B.3cosa米 C.米 D.米
A
5.(2019·衢州)如图,人字梯AB,AC的长都为2米,当α=50°时,人字梯顶端离地面的高度 AD是__ 米.(结果精确到0.1 m.参考数据∶sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
5
6.(2018·金华)如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为( )
B
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
一、理解并熟记以下关系:
课堂小结
二、特别注意:解决“直角三角形”问题时:
1、善于画图来分析解答;
2、在非直角三角形问题中,要善于通过作出适当的“垂线”将问题转化成“直角三角形”问题;
3、遇到某些不能直接计算的问题时,要灵活设定未知数来解决问题.
§1.4 解直角三角形
北师版九年级下册 直角三角形的三边关系
学习目标
1.理解 解直角三角形的意义;(重点)
2.理解解直角三角形的方法并能熟练解题. (重点、难点)
3、通过本节的学习进一步提升学生综合分析、解决问题的能力。
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,
tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
回顾与思考
例题精讲
【例1】 如图,在Rt△ABC中,∠C=90°, ,求这个直角三角形的其他元素.
解:在Rt△ABC中,a2+b2=c2,
∵a=√15,b=√5
∴∠B=30°
∠A=90°-30°=60°
一、知道两边长,求其它元素
像上述问题中,知道直角三角形某两个元素,求出其它元素的方法,叫做解直角三角形。
那么在Rt△ABC中,如果知道一个锐角,一条边长,你能求出其它元素吗?接下来我们继续探讨一下。
归纳小结
【例2】 如图,在Rt△ABC中,∠C=90°,b=30, ∠B=25°,求这个直角三角形的其他元素.
二、知道一个锐角,一条边长,求其它元素
例题精讲
解:在Rt△ABC中,∠C=90°,∠B=25°
∴∠A=65°
∵ sinB=b=30
∴tanB=
a==
(注意:sin25°≈0.42,tan25°≈0.47)
归纳小结
通过上述两个问题的讨论,大家慢慢会发现,在直角三角形中,只要知道一个边,和另一个元素,其它元素均可算出。
小组PK“加分赛”
在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,
根据下列条件求出直角三角形的其他元素(角度精确到1°)∶
(1)已知a=4,b=8;(提示:tan27°≈0.5)
(2)已知b=10,∠B=60°;
(3)己知c=20,∠A=60°.
解:(1)在Rt△ABC中,∠C=90°,a=4,b=8.
∴c=
∵tanA=
∴∠A≈27°,∠B≈63°.
解:(2)在Rt△ABC中,∠C=90°,∠B=60°,
∴∠A=30°.
∵ tanB= ,b=10,
∴a= .
∵ sinB= ,b=10,
∴c= .
解:(3)在Rt△ABC中,∠C=90°,∠A=60°,
∴∠B=30°.
∵ cosA= ,c=20,
∴b=10.
∵ sinA= ,c=20,
∴a= .
个人限时“加分赛”
2.在Rt△ABC'中,∠C=90°、∠A、∠B、∠C所对的边分别为a,b、c、根据下列条件求出直角二角形的其他元素∶
(1)c=20、∠A=45°: (2)a=36、∠B=30°
解:(1)∵tanA=
∴b=20,∠B=45°
∴c
(2)∵∠B=30°
∵sinA=
∴c=
∴∠A=60°
∵sinB=
∴b=
【例3】如图,在△ABC中,AC=6,BC=8,∠C=60°.求△ABC的面积。
拓展提升
解:作BD⊥AC.
∵∠C=60°,BC=8
∴CD=4,BD=4√3
∵S△ABC=1/2×AC×BD
∴S△ABC=12√3
分析:根据三角形性面积=1/2底×高,可以考虑作BC边上(或AC边上的高),利用∠C=30°,求出高即可。
变式1
在△ABC中,AC=6,BC=8,∠C= 30°. 求△ABC的面积。
变式2
在△ABC中,AC=6,BC=8,∠C= α. 求△ABC的面积。
变式3
在△ABC中,AC= b,BC= a,∠C= α. 求△ABC的面积。
解:略。
S△ABC=12
解:略。
S△ABC=12sinC
解:略。
S△ABC=1/2absinC
1、(2018·天津) cos30°的值为( )
A.√2/2 B.√3/2 C.1 D.√3
2.(2018·孝感)如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA 的值为( )
A. B. C. D.
B
A
中考链接
3.(2018·宜昌)如图,要测量小河两岸相对的两点P,A间的距离,可以在小河边取PA的垂线PB上一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于( )
A.100sin35°米 B.100sin55°米 C.100tan35°米 D.100tan55°米
C
4、(2019·长春)如图,一把梯子靠在垂直水平地面的墙上,梯子AB的长是3米.若梯子与地面的夹角为α,则梯子顶端到地面的距离 BC为( )
A.3sina米 B.3cosa米 C.米 D.米
A
5.(2019·衢州)如图,人字梯AB,AC的长都为2米,当α=50°时,人字梯顶端离地面的高度 AD是__ 米.(结果精确到0.1 m.参考数据∶sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
5
6.(2018·金华)如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为( )
B
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
一、理解并熟记以下关系:
课堂小结
二、特别注意:解决“直角三角形”问题时:
1、善于画图来分析解答;
2、在非直角三角形问题中,要善于通过作出适当的“垂线”将问题转化成“直角三角形”问题;
3、遇到某些不能直接计算的问题时,要灵活设定未知数来解决问题.
