1.5 三角函数的应用 课件(共18张PPT)
文档属性
| 名称 | 1.5 三角函数的应用 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:56:23 | ||
图片预览



文档简介
(共17张PPT)
§1.5 三角形函数的应用
北师版九年级下册 直角三角形的三边关系
学习目标
1、经历应用三角函数解决实际问题的过程,进一步体会三角函数在解决问题过程的意义;
2、理解方位角、仰角、俯角的概念并能运用其解决相关应用问题;(重点)
3、深刻体会“背靠背”模型在解题中的运用,并能融会贯通地去解决各类问题.(难点)
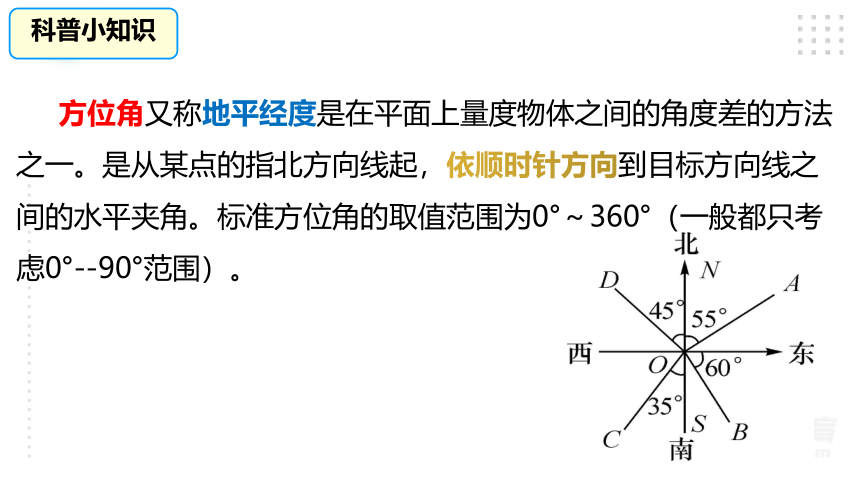
科普小知识
方位角又称地平经度是在平面上量度物体之间的角度差的方法之一。是从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角。标准方位角的取值范围为0°~360°(一般都只考虑0°--90°范围)。
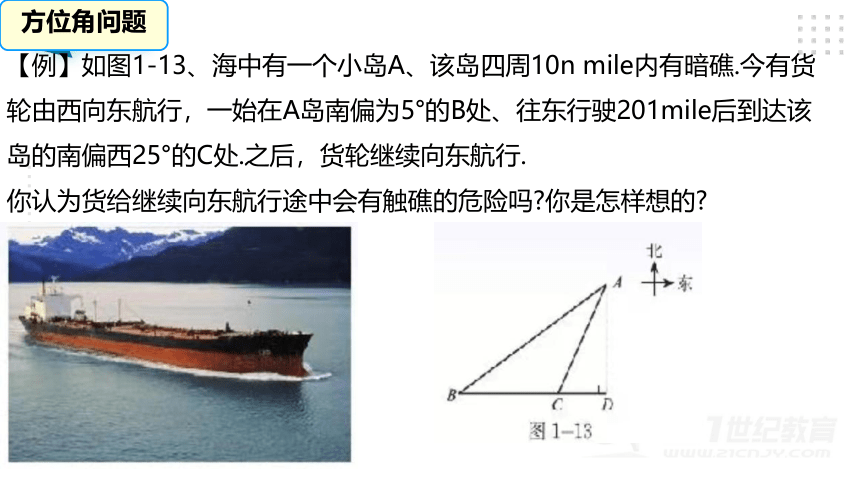
【例】如图1-13、海中有一个小岛A、该岛四周10n mile内有暗礁.今有货轮由西向东航行,一始在A岛南偏为5°的B处、往东行驶201mile后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.
你认为货给继续向东航行途中会有触礁的危险吗 你是怎样想的
方位角问题
解∶不会有触礁的危险.
如图,过点A作AD⊥BD交BC的延长线于点D.
设AD的长为xn mile. ∵AD⊥BD,∴∠ADB=90°,
∴△ACD,△ABD为直角三角形.
tan 55°=,tan25°=
∴BD≈1.4x,CD≈0.5x. ∵BD-CD =BC,∴1.4x-0.5x= 20,
即 0.9x = 20,解得x= >10
答∶货轮继续向东航行不会有触礁的危险.
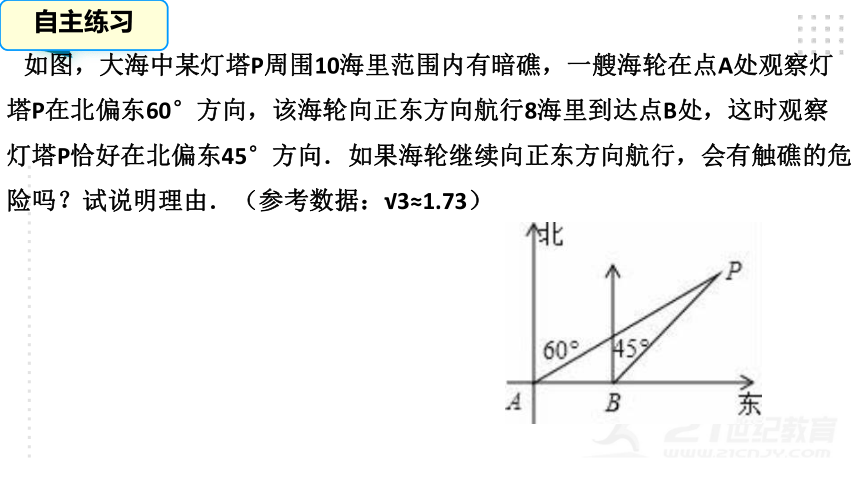
如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向.如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由.(参考数据:√3≈1.73)
自主练习
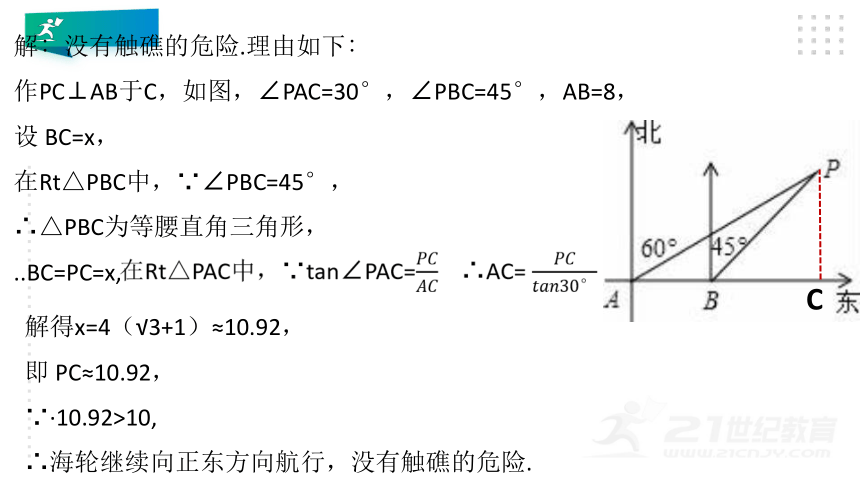
解∶没有触礁的危险.理由如下∶
作PC⊥AB于C,如图,∠PAC=30°,∠PBC=45°,AB=8,
设 BC=x,
在Rt△PBC中,∵∠PBC=45°,
∴△PBC为等腰直角三角形,
..BC=PC=x,
解得x=4(√3+1)≈10.92,
即 PC≈10.92,
∵·10.92>10,
∴海轮继续向正东方向航行,没有触礁的危险.
C
【例2】如图,一艘货轮以36kn的速度在海面上航行,当它有驶到A交时,发现它的东北方向有一灯塔B.货轮继续句北航行40min后到达C处.发现灯塔B在它北偏东75°方向、求此时货轮与灯塔B的距离(结果精确到0.01n mie).
方位角问题
分析:通过初步审题,会发现一时不易找出算法。所以,遇见此种图形,大家今后一定要留意它的辅助线添法——
45°
30°
“背靠背”型
解:如图所示∶过点C作CD⊥AB于点D,
∵∠A=45°,∠1=75°,∠ACD=45°,∠DCB=60°, 则∠B=30°,
则DC=ACsin45°=24x√2/2=12√2(km)
故BC=2CD=24√2≈33.9(km)
答∶此时货轮与灯塔B的距离约为33.9km.
D
∵一艘货轮以36km的速度在海面上航行,
向北航行40min后到达C点,
∴AC=36×2/3=24(km)
方法总结
运用解直角三角形的知识解决实际问题的步骤:
(1)将实际问题抽象为数学问题——画出平面图形;
(2)适当添加垂线,将问题转化为解直角三角形的问题;
(3)根据条件的特点,选用适当的锐角三角形函数来求出答案
特别注意:关键的解题模型——“背靠背”型
45°
30°
【例1】如图1-14、小明想测量塔CD的高度.他在A 处仰里塔顶,测得仰角为30°,再往塔的方向前进50m 至 B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m)
仰角、俯角问题
想一想
【例2】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
仰角、俯角问题
分析:解本题,需要用到“方程思想”一般情况下,所问即所设——设EF=x米。当然此题也可以仅设EG的高为x米。
CA=DB= BG-DG=(x-1.5)米.
仰角、俯角问题
分析:此题较为简单,主要是找准需用的“直角三角形”,比如,第一问考虑使用Rt△BAC,第二问考虑使用Rt△DCE,借助解直角三角形的方法即可轻松解决。
AC=20√3米
CD=(80√3-120)米
当堂测试
1、(2019·孝感)如图,在P处利用测角仪B测得某建筑物 AB 的顶端B 点的仰角为60°,点C的仰角为45°,点P到建筑物的距离为 PD=20 米,
则 BC= 米.
(20√3-20)
提示:此题较为简单,通过观察可以发现PD分别位于两个直角三角形Rt△CDP和Rt△BDP中, 借助解直角三角形的方法分别算出BD和CD即可。
2、有--座建筑物,在地面上 A点测得其顶点C的仰角为30°,向建筑物前进 50m到B点,又测得C的仰角为45°,求建筑物的高度(结果精确到0.1m,√2≈1.414,√3≈1.732).
当堂测试
分析:此题主要是用好“数形结合思想”,正确画出草图,并且所问即所设,设出楼高CD=x米以后,分别利用其在Rt△CDB和Rt△ADC,表示出DA并借助∠A=30°,利用AD=√3CD,列出方程,即可轻松解决。
最后注意保留一位小数。
楼高CD=25+25√3≈68.3米
课堂小结
1、通过本节课的初步学习,熟知“方位角”“仰角、俯角”的概念;
2、注意解实际问题中的解题模型——“背靠背”的运用,逐步体会,并灵活掌握不同问题中的运用;
3、要加强对图形的认知,善于依据问题,画出问题图形,以便准确分析问题,同时深刻体会“方程思想”的重要应用.
§1.5 三角形函数的应用
北师版九年级下册 直角三角形的三边关系
学习目标
1、经历应用三角函数解决实际问题的过程,进一步体会三角函数在解决问题过程的意义;
2、理解方位角、仰角、俯角的概念并能运用其解决相关应用问题;(重点)
3、深刻体会“背靠背”模型在解题中的运用,并能融会贯通地去解决各类问题.(难点)
科普小知识
方位角又称地平经度是在平面上量度物体之间的角度差的方法之一。是从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角。标准方位角的取值范围为0°~360°(一般都只考虑0°--90°范围)。
【例】如图1-13、海中有一个小岛A、该岛四周10n mile内有暗礁.今有货轮由西向东航行,一始在A岛南偏为5°的B处、往东行驶201mile后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.
你认为货给继续向东航行途中会有触礁的危险吗 你是怎样想的
方位角问题
解∶不会有触礁的危险.
如图,过点A作AD⊥BD交BC的延长线于点D.
设AD的长为xn mile. ∵AD⊥BD,∴∠ADB=90°,
∴△ACD,△ABD为直角三角形.
tan 55°=,tan25°=
∴BD≈1.4x,CD≈0.5x. ∵BD-CD =BC,∴1.4x-0.5x= 20,
即 0.9x = 20,解得x= >10
答∶货轮继续向东航行不会有触礁的危险.
如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向.如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由.(参考数据:√3≈1.73)
自主练习
解∶没有触礁的危险.理由如下∶
作PC⊥AB于C,如图,∠PAC=30°,∠PBC=45°,AB=8,
设 BC=x,
在Rt△PBC中,∵∠PBC=45°,
∴△PBC为等腰直角三角形,
..BC=PC=x,
解得x=4(√3+1)≈10.92,
即 PC≈10.92,
∵·10.92>10,
∴海轮继续向正东方向航行,没有触礁的危险.
C
【例2】如图,一艘货轮以36kn的速度在海面上航行,当它有驶到A交时,发现它的东北方向有一灯塔B.货轮继续句北航行40min后到达C处.发现灯塔B在它北偏东75°方向、求此时货轮与灯塔B的距离(结果精确到0.01n mie).
方位角问题
分析:通过初步审题,会发现一时不易找出算法。所以,遇见此种图形,大家今后一定要留意它的辅助线添法——
45°
30°
“背靠背”型
解:如图所示∶过点C作CD⊥AB于点D,
∵∠A=45°,∠1=75°,∠ACD=45°,∠DCB=60°, 则∠B=30°,
则DC=ACsin45°=24x√2/2=12√2(km)
故BC=2CD=24√2≈33.9(km)
答∶此时货轮与灯塔B的距离约为33.9km.
D
∵一艘货轮以36km的速度在海面上航行,
向北航行40min后到达C点,
∴AC=36×2/3=24(km)
方法总结
运用解直角三角形的知识解决实际问题的步骤:
(1)将实际问题抽象为数学问题——画出平面图形;
(2)适当添加垂线,将问题转化为解直角三角形的问题;
(3)根据条件的特点,选用适当的锐角三角形函数来求出答案
特别注意:关键的解题模型——“背靠背”型
45°
30°
【例1】如图1-14、小明想测量塔CD的高度.他在A 处仰里塔顶,测得仰角为30°,再往塔的方向前进50m 至 B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m)
仰角、俯角问题
想一想
【例2】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
仰角、俯角问题
分析:解本题,需要用到“方程思想”一般情况下,所问即所设——设EF=x米。当然此题也可以仅设EG的高为x米。
CA=DB= BG-DG=(x-1.5)米.
仰角、俯角问题
分析:此题较为简单,主要是找准需用的“直角三角形”,比如,第一问考虑使用Rt△BAC,第二问考虑使用Rt△DCE,借助解直角三角形的方法即可轻松解决。
AC=20√3米
CD=(80√3-120)米
当堂测试
1、(2019·孝感)如图,在P处利用测角仪B测得某建筑物 AB 的顶端B 点的仰角为60°,点C的仰角为45°,点P到建筑物的距离为 PD=20 米,
则 BC= 米.
(20√3-20)
提示:此题较为简单,通过观察可以发现PD分别位于两个直角三角形Rt△CDP和Rt△BDP中, 借助解直角三角形的方法分别算出BD和CD即可。
2、有--座建筑物,在地面上 A点测得其顶点C的仰角为30°,向建筑物前进 50m到B点,又测得C的仰角为45°,求建筑物的高度(结果精确到0.1m,√2≈1.414,√3≈1.732).
当堂测试
分析:此题主要是用好“数形结合思想”,正确画出草图,并且所问即所设,设出楼高CD=x米以后,分别利用其在Rt△CDB和Rt△ADC,表示出DA并借助∠A=30°,利用AD=√3CD,列出方程,即可轻松解决。
最后注意保留一位小数。
楼高CD=25+25√3≈68.3米
课堂小结
1、通过本节课的初步学习,熟知“方位角”“仰角、俯角”的概念;
2、注意解实际问题中的解题模型——“背靠背”的运用,逐步体会,并灵活掌握不同问题中的运用;
3、要加强对图形的认知,善于依据问题,画出问题图形,以便准确分析问题,同时深刻体会“方程思想”的重要应用.
