苏科版八年级数学上册 3.3 勾股定理的简单应用课件(19张)
文档属性
| 名称 | 苏科版八年级数学上册 3.3 勾股定理的简单应用课件(19张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 10:53:17 | ||
图片预览





文档简介
(共19张PPT)
八年级(上册)
初中数学
3.3 勾股定理的简单应用
一、预习·质疑
1.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,且 ,则这个三角形是_________三角形, __________为直角
2. 一个直角三角形的两直角边分别为3和4, 其斜边上的高是__________
3.要登上8m高的建筑物,为了安全需要,需使梯子底端离建筑物6m.问至少需要 米的梯子?
4.小明和小强的跑步速度分别是6m/s和8m/s,他们同时从同一地点分别向东、南练习跑步,那么从出发开始需__________s可以相距100m
直角
2.4
10
10
1.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,且 ,则这个三角形是_________三角形, __________为直角
2. 一个直角三角形的两直角边分别为3和4, 其斜边上的高是__________
3.要登上8m高的建筑物,为了安全需要,需使梯子底端离建筑物6m.问至少需要 米的梯子?
4.小明和小强的跑步速度分别是6m/s和8m/s,他们同时从同一地点分别向东、南练习跑步,那么从出发开始需__________s可以相距100m
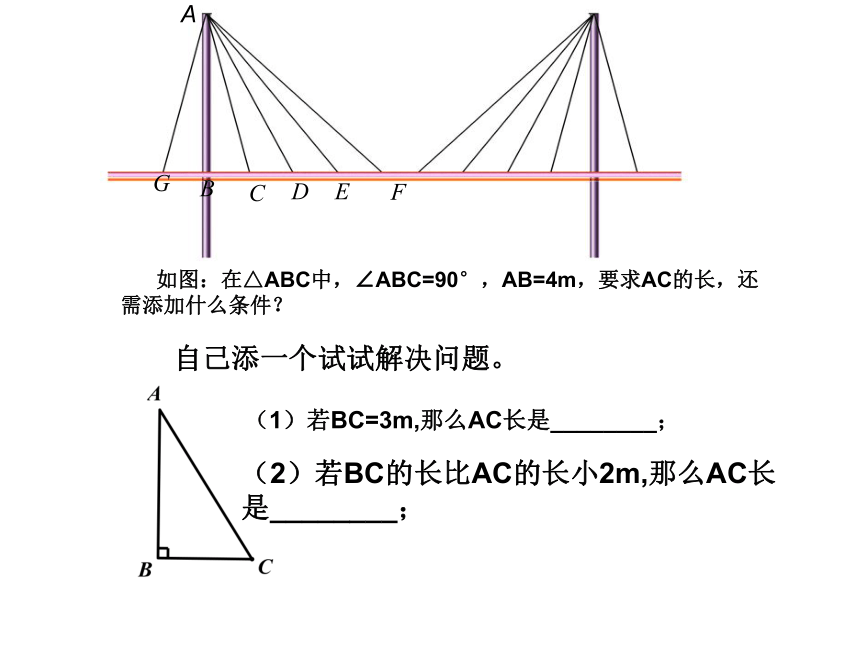
从远处看,斜拉桥的索塔、桥面与拉索组成许多直角三角形.
观察
已知桥面以上索塔AB的高,怎样计算AC、AD、AE、AF、AG的长.
A
B
C
E
F
G
D
如图:在△ABC中,∠ABC=90°,AB=4m,要求AC的长,还需添加什么条件?
自己添一个试试解决问题。
(1)若BC=3m,那么AC长是________;
(2)若BC的长比AC的长小2m,那么AC长是________;
B
C
E
F
G
D
A
九章算术中的“折竹”问题:今有竹高一丈,末折抵地,去根三尺,问折者高几何?
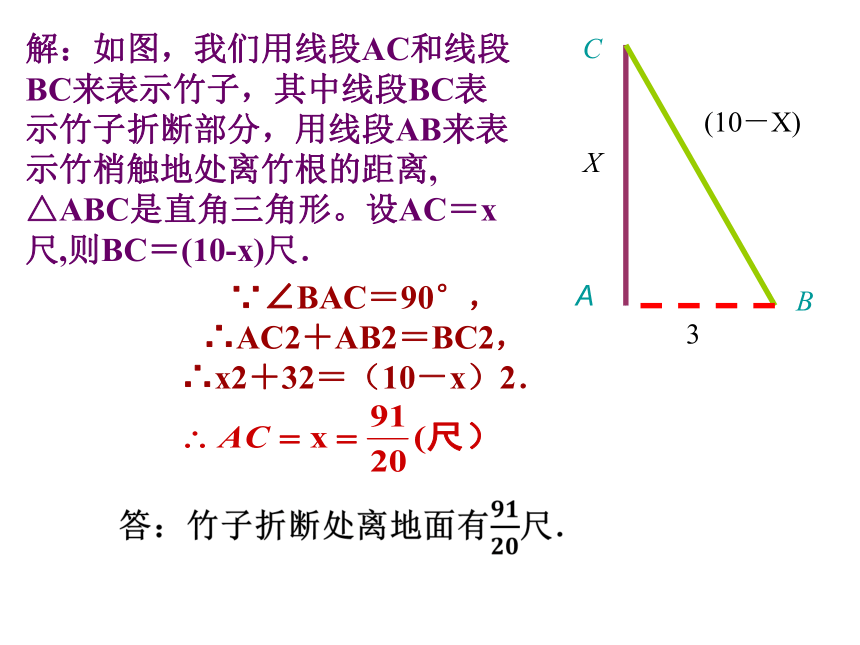
意思是:有一根意竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?
解:如图,我们用线段AC和线段BC来表示竹子,其中线段BC表示竹子折断部分,用线段AB来表示竹梢触地处离竹根的距离, △ABC是直角三角形。设AC=x尺,则BC=(10-x)尺.
∵∠BAC=90°,
∴AC2+AB2=BC2,
∴x2+32=(10-x)2.
C
B
X
(10-X)
3
A
拓展延伸
1.如图,有大小两棵树,大树AB高是8米,小树CD高是3米,两棵树的水平距离BD是12米,一只小鸟从小树顶C飞到大树顶A,至少飞多少米?
生活问题
2·小亮和同学们在操超场上玩,抬头仰望五星红旗,大家想知道旗杆到底有多高.小亮发现杆上绳子垂到地面多2米,把绳子下端拉离旗杆底8米,下端刚好接触地面,你能解决这个问题吗?请先画图,再解决这个问题.
例1: 如图,在△ABC中, AB=26,BC=20,BC边上的中线AD=24,求AC.
D
C
B
A
∴BD=CD= BC= ×20=10.
∵AD2+BD2=576+100=676,
AB 2=262=676,
解:∵AD是BC边上的中线,
∴AD2+BD2=AB2,
∴ ∠ADB=90°,AD垂直平分BC.
∴AC=AB=26.
D
C
B
A
26
20
24
变式1.如图,在△ABC中,AD⊥BC,AB=15,AD=12,AC=13,求△ABC的周长和面积.
D
C
B
A
周长为42
面积为84
变式2 .如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.求AG的长。
聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上。如图(1)所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的。若将树干的侧面展开成一个平面,如图(2),可清楚的看出葛藤在这个平面上是沿直线上升的。
(1)
(2)
数学奇闻
勾股定理与它的逆定理在应用上有什么区别?
勾股定理主要应用于求线段的长度、图形的周长、面积;
勾股定理的逆定理用于判断三角形的形状。
1、数形结合思想 2、转化思想
从勾股定理的应用中我们进一步体会到直角
三角形与等腰三角形有着密切的联系;把研究等
腰三角形转化为研究直角三角形,这是研究问题
的一种策略.
3.3 勾股定理的简单应用
变式3:在△ABC中AB=14,BC=15,AC=13,求△ABC面积。
变式4某农民开垦出一块三边长分别为7m,8m,9m三角形地块准备种植花生,聪明的同学你能帮他算一算这块地的面积吗?
《引葭赴岸》
“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个边长为10尺的正方形池塘,一棵芦苇AB生长在它的中央,高出水面部分BC为一尺。如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B’.问水深和芦苇长各为多少?
八年级(上册)
初中数学
3.3 勾股定理的简单应用
一、预习·质疑
1.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,且 ,则这个三角形是_________三角形, __________为直角
2. 一个直角三角形的两直角边分别为3和4, 其斜边上的高是__________
3.要登上8m高的建筑物,为了安全需要,需使梯子底端离建筑物6m.问至少需要 米的梯子?
4.小明和小强的跑步速度分别是6m/s和8m/s,他们同时从同一地点分别向东、南练习跑步,那么从出发开始需__________s可以相距100m
直角
2.4
10
10
1.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,且 ,则这个三角形是_________三角形, __________为直角
2. 一个直角三角形的两直角边分别为3和4, 其斜边上的高是__________
3.要登上8m高的建筑物,为了安全需要,需使梯子底端离建筑物6m.问至少需要 米的梯子?
4.小明和小强的跑步速度分别是6m/s和8m/s,他们同时从同一地点分别向东、南练习跑步,那么从出发开始需__________s可以相距100m
从远处看,斜拉桥的索塔、桥面与拉索组成许多直角三角形.
观察
已知桥面以上索塔AB的高,怎样计算AC、AD、AE、AF、AG的长.
A
B
C
E
F
G
D
如图:在△ABC中,∠ABC=90°,AB=4m,要求AC的长,还需添加什么条件?
自己添一个试试解决问题。
(1)若BC=3m,那么AC长是________;
(2)若BC的长比AC的长小2m,那么AC长是________;
B
C
E
F
G
D
A
九章算术中的“折竹”问题:今有竹高一丈,末折抵地,去根三尺,问折者高几何?
意思是:有一根意竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?
解:如图,我们用线段AC和线段BC来表示竹子,其中线段BC表示竹子折断部分,用线段AB来表示竹梢触地处离竹根的距离, △ABC是直角三角形。设AC=x尺,则BC=(10-x)尺.
∵∠BAC=90°,
∴AC2+AB2=BC2,
∴x2+32=(10-x)2.
C
B
X
(10-X)
3
A
拓展延伸
1.如图,有大小两棵树,大树AB高是8米,小树CD高是3米,两棵树的水平距离BD是12米,一只小鸟从小树顶C飞到大树顶A,至少飞多少米?
生活问题
2·小亮和同学们在操超场上玩,抬头仰望五星红旗,大家想知道旗杆到底有多高.小亮发现杆上绳子垂到地面多2米,把绳子下端拉离旗杆底8米,下端刚好接触地面,你能解决这个问题吗?请先画图,再解决这个问题.
例1: 如图,在△ABC中, AB=26,BC=20,BC边上的中线AD=24,求AC.
D
C
B
A
∴BD=CD= BC= ×20=10.
∵AD2+BD2=576+100=676,
AB 2=262=676,
解:∵AD是BC边上的中线,
∴AD2+BD2=AB2,
∴ ∠ADB=90°,AD垂直平分BC.
∴AC=AB=26.
D
C
B
A
26
20
24
变式1.如图,在△ABC中,AD⊥BC,AB=15,AD=12,AC=13,求△ABC的周长和面积.
D
C
B
A
周长为42
面积为84
变式2 .如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.求AG的长。
聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上。如图(1)所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的。若将树干的侧面展开成一个平面,如图(2),可清楚的看出葛藤在这个平面上是沿直线上升的。
(1)
(2)
数学奇闻
勾股定理与它的逆定理在应用上有什么区别?
勾股定理主要应用于求线段的长度、图形的周长、面积;
勾股定理的逆定理用于判断三角形的形状。
1、数形结合思想 2、转化思想
从勾股定理的应用中我们进一步体会到直角
三角形与等腰三角形有着密切的联系;把研究等
腰三角形转化为研究直角三角形,这是研究问题
的一种策略.
3.3 勾股定理的简单应用
变式3:在△ABC中AB=14,BC=15,AC=13,求△ABC面积。
变式4某农民开垦出一块三边长分别为7m,8m,9m三角形地块准备种植花生,聪明的同学你能帮他算一算这块地的面积吗?
《引葭赴岸》
“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个边长为10尺的正方形池塘,一棵芦苇AB生长在它的中央,高出水面部分BC为一尺。如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B’.问水深和芦苇长各为多少?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
