2021-2022学年华东师大版数学七年级上册3.3.2多项式课件(21张)
文档属性
| 名称 | 2021-2022学年华东师大版数学七年级上册3.3.2多项式课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 11:01:45 | ||
图片预览


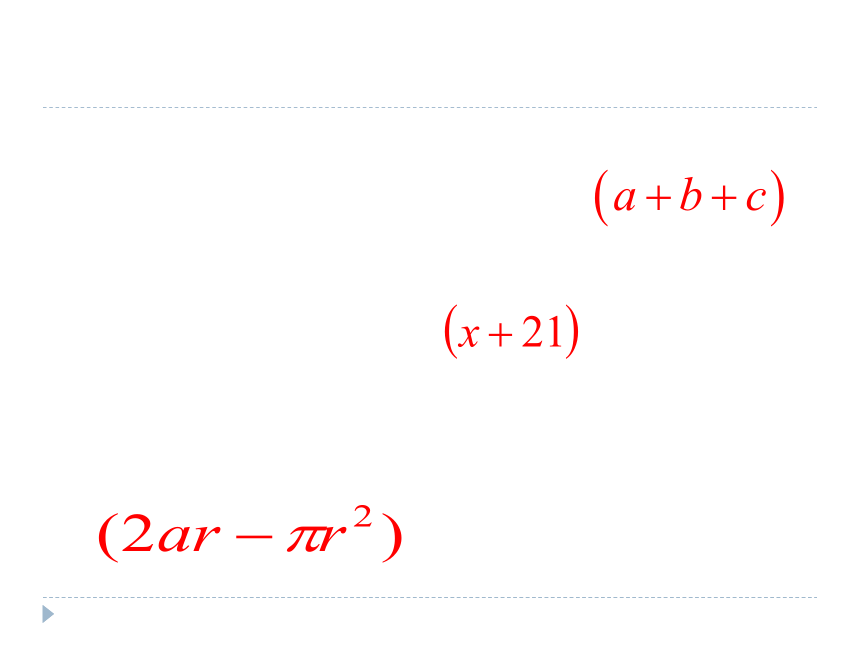





文档简介
(共21张PPT)
多 项 式
3.3 多项式
学习目标
1、掌握多项式、多项式的项、项数、次数,以及常数项的概念。
3、归纳出整式的概念。会区别单项式和多项式。
2、会准确迅速地确定一个多项式的项数和次数。
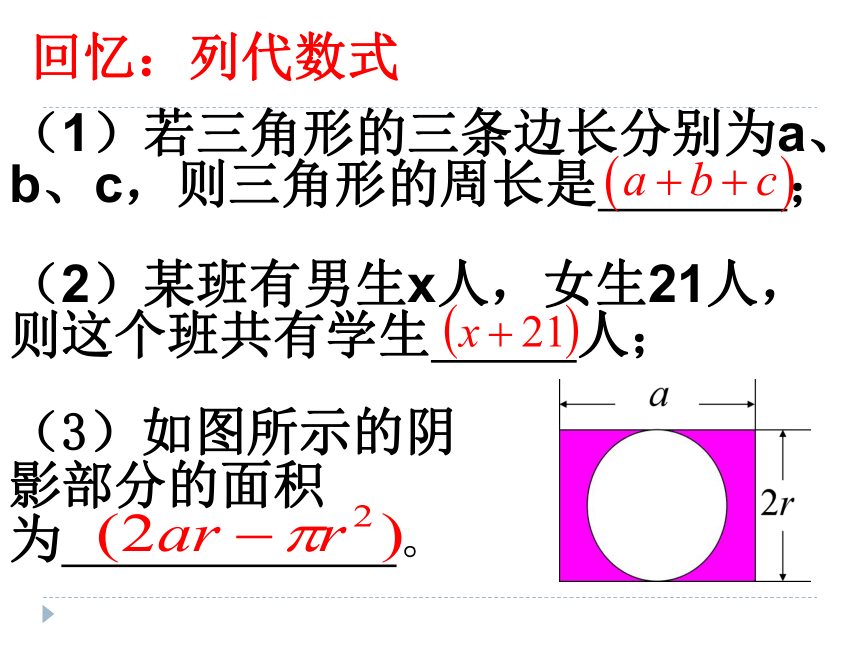
(1)若三角形的三条边长分别为a、b、c,则三角形的周长是 ;
(2)某班有男生x人,女生21人,则这个班共有学生 人;
回忆:列代数式
(3)如图所示的阴影部分的面积为 。
这些代数式有什么特点
特点:由单项式
相加构成的.
多项式的概念
几个单项式的和叫做多项式。
多项式中每个单项式叫
多项式的项。
不含字母的项,叫常数项。
一个多项式含有几项就叫
几项式。
多项式里,次数最高项的
次数, 就是多项式的次数。
1、这个多项式共有几项 是哪几项
2、这个多项式的次数是什么
这个多项式的项有 、 、
是常数项.
是一次项,
是二次项,
这个多项式的次数是2.
多项式的命名
一个多项式含有几项就叫
几项式。
多项式里,次数最高项的
次数, 就是多项式的次数。
多项式一般命名为几次几项式。
你能给左边的多项式
命名吗?
多项式的命名
二次三项式
一次三项式
一次二项式
二次二项式
理解并判断:
(1)多项式a3-a2b+ab2-b3的项为a3、a2b、ab2、b3,次数为12;
(2)多项式3n4-2n2+1的次数为4,常数项为1。
注意!
1、多项式的次数为最高次项的次数 。
2、多项式的每一项都包括它前面的符号。
√
×
例题解析:
例1 指出下列多项式的项和次数:
(1)2x-1+3x2 (2)4x3+2x2y2-2y2
解:(1)多项式2x-1+3x2的项有 2x、-1、3x2,次数是2.
(2)多项式4x3+2x2y2-2y2的项有 4x3 、2x2y2 、-2y2 , 次数是4.
例题解析:
例2 指出下列多项式是几次几项式。
(1)x3-x+1
(2)x3-2x2y2+3y2
【注意】几次几项式的答法: 用中文的一、二、三……等来答。
解: (1) x3 -x+1 是三次三项式
(2)x3-2x2y2+3y2 是四次三项式
课内探讨
想一想:多项式的次数与单项式的次数有什么区别和联系?
从定义来区分:
多项式里,次数最高项的次数,就是多项式的次数。
一个单项式中,所有字母的指数的和,叫做这个单项式的次数。
单项式与多项式统称整式。
整式定义
你能说出单项式、多项式、整式之间的关系吗?
1、判断下列各代数式是否是整式?
(1)–1; (2)r; (3)
(4) ;(5) ;(6)
2、 是 次 项式,其中三次项系数是 ,二次项为 ,常数项为 ,写出所有的项 。 【注意】某一项的次数是几就叫几次项。
三
三
1
3、指出下列多项式是几次几项式:
(1)2x+1+3 x2
(2)1+ 4m4
(3)2 x2-3xy+y2
(4)4 x3+2x-3y2
思维升级
1.多项式3x2n +6x-1是关于x的二次三项式(n是正整数),求n的值。
2.已知代数式3xn-(m-1)x+1是关于x的三次二项式,求m、n的值。
1、多项式的定义,多项式的项,多项式的次数及常数项。
课堂小结:
2、整式。
作业:
P100 习题
3.3第2、3题
多 项 式
3.3 多项式
学习目标
1、掌握多项式、多项式的项、项数、次数,以及常数项的概念。
3、归纳出整式的概念。会区别单项式和多项式。
2、会准确迅速地确定一个多项式的项数和次数。
(1)若三角形的三条边长分别为a、b、c,则三角形的周长是 ;
(2)某班有男生x人,女生21人,则这个班共有学生 人;
回忆:列代数式
(3)如图所示的阴影部分的面积为 。
这些代数式有什么特点
特点:由单项式
相加构成的.
多项式的概念
几个单项式的和叫做多项式。
多项式中每个单项式叫
多项式的项。
不含字母的项,叫常数项。
一个多项式含有几项就叫
几项式。
多项式里,次数最高项的
次数, 就是多项式的次数。
1、这个多项式共有几项 是哪几项
2、这个多项式的次数是什么
这个多项式的项有 、 、
是常数项.
是一次项,
是二次项,
这个多项式的次数是2.
多项式的命名
一个多项式含有几项就叫
几项式。
多项式里,次数最高项的
次数, 就是多项式的次数。
多项式一般命名为几次几项式。
你能给左边的多项式
命名吗?
多项式的命名
二次三项式
一次三项式
一次二项式
二次二项式
理解并判断:
(1)多项式a3-a2b+ab2-b3的项为a3、a2b、ab2、b3,次数为12;
(2)多项式3n4-2n2+1的次数为4,常数项为1。
注意!
1、多项式的次数为最高次项的次数 。
2、多项式的每一项都包括它前面的符号。
√
×
例题解析:
例1 指出下列多项式的项和次数:
(1)2x-1+3x2 (2)4x3+2x2y2-2y2
解:(1)多项式2x-1+3x2的项有 2x、-1、3x2,次数是2.
(2)多项式4x3+2x2y2-2y2的项有 4x3 、2x2y2 、-2y2 , 次数是4.
例题解析:
例2 指出下列多项式是几次几项式。
(1)x3-x+1
(2)x3-2x2y2+3y2
【注意】几次几项式的答法: 用中文的一、二、三……等来答。
解: (1) x3 -x+1 是三次三项式
(2)x3-2x2y2+3y2 是四次三项式
课内探讨
想一想:多项式的次数与单项式的次数有什么区别和联系?
从定义来区分:
多项式里,次数最高项的次数,就是多项式的次数。
一个单项式中,所有字母的指数的和,叫做这个单项式的次数。
单项式与多项式统称整式。
整式定义
你能说出单项式、多项式、整式之间的关系吗?
1、判断下列各代数式是否是整式?
(1)–1; (2)r; (3)
(4) ;(5) ;(6)
2、 是 次 项式,其中三次项系数是 ,二次项为 ,常数项为 ,写出所有的项 。 【注意】某一项的次数是几就叫几次项。
三
三
1
3、指出下列多项式是几次几项式:
(1)2x+1+3 x2
(2)1+ 4m4
(3)2 x2-3xy+y2
(4)4 x3+2x-3y2
思维升级
1.多项式3x2n +6x-1是关于x的二次三项式(n是正整数),求n的值。
2.已知代数式3xn-(m-1)x+1是关于x的三次二项式,求m、n的值。
1、多项式的定义,多项式的项,多项式的次数及常数项。
课堂小结:
2、整式。
作业:
P100 习题
3.3第2、3题
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
