人教版九年级上册数学22.1.4二次函数的图象和性质教学设计
文档属性
| 名称 | 人教版九年级上册数学22.1.4二次函数的图象和性质教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 76.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 11:17:56 | ||
图片预览



文档简介
《二次函数的图象和性质》教学设计
一、内容和内容解析
(一)内容
二次函数的图象和性质.
(二)内容解析
类比一次函数图象和性质的研究,采用从特殊函数到一般函数的研究方法.最简单二次函数的图象和性质,对a>0、a<0分别进行探究.通过用描点法在同一坐标系内画出的图象,引导学生观察这些函数图象的共同点和不同点,归纳得出二次函数的的图象和性质,同样类比研究的性质,最后从对称性、最值、增减性几个方面归纳出,体现了研究代数学问题的一般方法.
二、目标和目标解析
(一)教学目标
1.理解并掌握二次函数的图象和性质;
2.经历、探索二次函数图象性质的过程,学会研究函数性质的方法,培养观察、思考、归纳的良好思维习惯.
重点与难点:
重点:二次函数的图象和性质.
难点:数形结合探讨二次函数的图象和性质.
(二)目标解析
1.二次函数性质是由解析式和自变量取值范围决定的,所以从解析式分析得到函数图象的示意图和函数的性质,用图象来验证性质.
2.通过对多个函数图象的对比,发现共性,归纳函数的性质,帮助学生直观地理解二次函数的性质.
三、教学问题诊断分析
画二次函数的图象时学生容易出现的问题是点与点之间用折线连接,尤其在顶点附近部分图象画不好,可以让学生多画几对点,图象本身就是近似的,点取的越多越接近于标准.
本节课突出培养从特殊到一般、数形结合和类比思想解决问题,为学生学习后续函数、研究后续函数的图形和性质奠定扎实的基础.
本课的教学重点是理解二次函数的图象和性质,从解析式、表格、图象三种途径分别发现函数性质、理解函数性质.
本课的教学难点是二次函数的图象和性质的探究过程.
四、教学过程设计
(一)温故知新
1.回顾研究一次函数的基本方法:概念→图象和性质→应用性质.
2.按怎样的顺序研究一次函数的图象和性质?
令b=0,特殊的一次函数即正比例函数→b≠0的一次函数 ,可以通过正比例函数上下平移或左右平移得到即特殊→一般.
3.如何来研究二次函数的图形和性质呢?
引导学生仿照一次函数的研究方法,从特殊形式的二次函数入手,如:令时或令时或令时,从最简单、最特殊的形式开始研究,从而引出本节课的重点:探究二次函数的图象和性质.
师生活动:回忆一次函数的研究顺序,寻找最特殊的二次函数并入手研究二次函数的性质.
【设计意图】回顾一次函数的研究程序:概念→图象和性质→应用,类比研究二次函数的图象和性质.既巩固函数的研究方法,又引出今天学习的内容.
(二)合作交流,探究性质
1.从最简单的二次函数开始研究它的图象和性质.分a>0 和a<0,先研究a>0,并从a=1入手探究的图象和性质.
(1)从解析式研究函数的图象和性质.
从解析式研究下面的内容:
①自变量取值范围:x取全体实数;
②函数值y的取值范围:;
③当x取相反数时,函数y值相等;(对称性)
④当x=0时,y有最小值,y的最小值为0;
⑤当时,y随着x的增大而增大,当时,y随着x的增大而减小;
⑥图象分布于第一、二象限和原点;
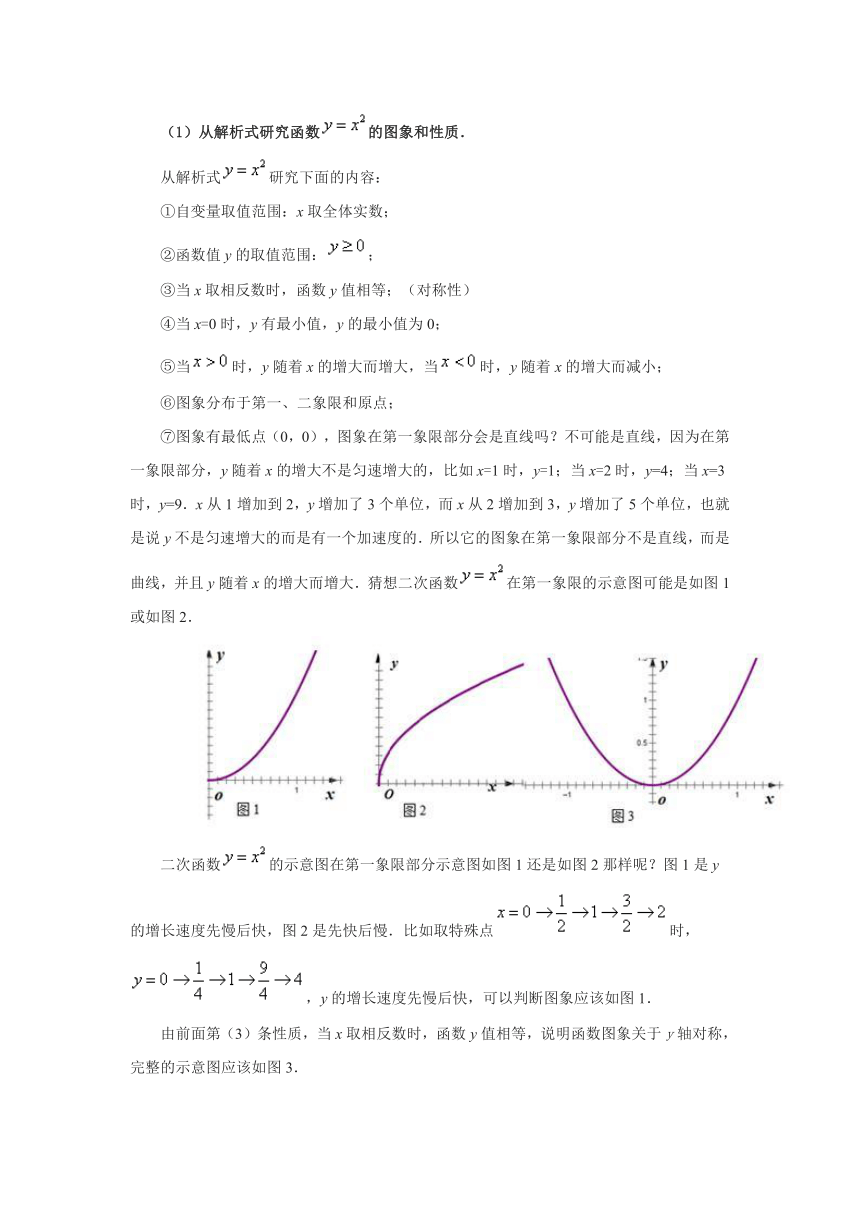
⑦图象有最低点(0,0),图象在第一象限部分会是直线吗?不可能是直线,因为在第一象限部分,y随着x的增大不是匀速增大的,比如x=1时,y=1;当x=2时,y=4;当x=3时,y=9.x从1增加到2,y增加了3个单位,而x从2增加到3,y增加了5个单位,也就是说y不是匀速增大的而是有一个加速度的.所以它的图象在第一象限部分不是直线,而是曲线,并且y随着x的增大而增大.猜想二次函数在第一象限的示意图可能是如图1或如图2.
二次函数的示意图在第一象限部分示意图如图1还是如图2那样呢?图1是y的增长速度先慢后快,图2是先快后慢.比如取特殊点时,,y的增长速度先慢后快,可以判断图象应该如图1.
由前面第(3)条性质,当x取相反数时,函数y值相等,说明函数图象关于y轴对称,完整的示意图应该如图3.
归纳二次函数的性质:
图象关于y轴对称; 图象有最低点(0,0); 在y轴左侧,y随着x的增大而减小;在y轴右侧,y随着x的增大而增大.
师生活动:由解析式分析函数图象和性质,从自变量和函数值范围、对称性、增减性、最值等几个方面分析,得到函数性质和猜想函数示意图.
【设计意图】学会从函数解析式研究函数性质的方法,了解对一个新函数应该从哪些内容、按什么顺序研究它的性质,为探究函数性质的知识体系打下基础,并从中积累基本的数学活动经验.
(2)从表格研究函数的图象和性质.
为了得到准确的的图象,用描点法来画.
描点法的步骤是列表、描点、连线.列表时根据自变量的对称性取一些有代表性的对称点,由于时,,估计学生画图时会出现问题,建议在0到1之间多取几对数,如.
引导学生从表格发现二次函数的性质:
图象关于y轴对称; 图象有最低点(0,0);在y轴左侧,y随着x的增大而减小;在y轴右侧,y随着x的增大而增大.
学生在画图过程中容易出现点与点之间用折线连接,突破的办法就是多取几对点,尤其是自变量在0在1之间.
师生活动:用描点法画准确的的图象,先列表,取代表性的一些特殊值,从表格探究函数的性质.
【设计意图】从表格发现函数的图象和性质,从多种角度帮助学生理解函数的图象和性质,突出重点,突破难点,为学生后续研究函数性质奠定基础.
(3)从图象研究函数的性质.
用描点法得到y= x2的图象,给图象命名.二次函数y= x2的图象形状类似于投篮或掷铅球时球在空中所经过的路线,只是这条曲线开口向上,这条曲线叫抛物线y= x2.
二次函数的图象都是抛物线.
一般地,二次函数的图象叫做抛物线 .
抛物线y= x2关于y轴对称,y轴是它的对称轴.
对称轴与抛物线的交点叫做抛物线的顶点.
抛物线y= x2在x轴上方(除顶点外),顶点是它的最低点,开口向上,并且向上无限伸展; 当x=0时,函数 y的值最小,最小值是0.
在对称轴左侧(或x<0时),y随着x的增大而减小;
在对称轴右侧(或x>0时),y随着x的增大而增大.
师生活动:对照描点法画出的y= x2.的图象,给图象命名.在经历解析式、表格分析函数性质的基础上,归纳二次函数y= x2.的性质.
【设计意图】用描点法画出准确的图象验证猜想所得示意图,对照图象研究函数性质.从解析式、列表、图象三种函数表示法分别研究函数性质,帮助学生理解函数的性质.
2.从特殊到一般地归纳函数的图象和性质
画一画:在同一坐标系中画出下列函数的图象:y= x2 、y= 2x2 、y=x2、、、,并比较它们的相同点与不同点.
让学生讨论、交流,达成共识,当时,抛物线开口向上,在对称轴的左侧,抛物线自左向右下降;在对称轴的右侧,抛物线自左向右上升,顶点是抛物线上位置最低点.图象的这些特点,反映了当时,函数的性质;当时,函数值y随x的增大而减小;与时,函数值y随x的增大而增大,当时,函数值取得最小值,最小值是y=0.
当时,抛物线开口向下,在对称轴的左侧,抛物线自左向右上升;在对称轴的右侧,抛物线自左向右下降,顶点是抛物线上位置最高点.图象的这些特点,反映了当时,函数的性质;当x<0时,函数值y随x的增大而增大;与x>0时,函数值y随x的增大而减小,当x=0时,函数值取得最大值,最大值是y=0.
师生活动:在同一坐标系中画出不同的函数图象,合作交流,归纳二次函数的图象和性质.
【设计意图】通过对函数图象的画和分析,让学生一方面熟悉二次函数图象,见到二次函数想到抛物线,另一方面归纳总结的性质,渗透从特殊到一般的方法.对于a对抛物线开口大小的影响,教师还可以借助几何画板演示,多展示一些抛物线,给学生以直观的形象,进一步加深理解.
(三)新知应用,加深理解
例1 (1)抛物线的顶点坐标是 ,对称轴是 ,在 侧,y随着x的增大而增大;在 侧,y随着x的增大而减小,当 x= 时,函数 y的值最 ,最 值是 ,抛物线在x轴的 方(除顶点外).
(2)抛物线在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的 ,当x = 0时,函数y的值最 ,最 值是 ;当x 0时,y < 0.
师生活动:直接应用函数的图象和性质,二次函数的图象分两类,开口向上和向下.
【设计意图】巩固刚学的图象和性质,要求学生见解析式想图象.
例2 已知二次函数.
(1)当m取何值时,它的图象开口向下;
(2)当x>0时,y随x的增大而增大,求函数关系式.
师生活动:联系二次函数概念,直接考查函数的图象和性质.
【设计意图】建构新旧知识体系,要求学生从函数性质想图象.
(四)巩固概念,学以致用
巩固练习:教科书32页练习,增加一问:说出函数的增减性.
【设计意图】见函数想图象,数形结合,巩固二次函数的图象和性质.
(五)归纳小结,反思提高
不仅总结今天所学的知识,重点归纳数学方法和数学思维.
1.从函数解析式、表格、图象研究函数图象和性质的几个方面:自变量取值范围,函数值取值范围,对称性,最值,增减性等.
2.二次函数的图象和性质.
3.数形结合──图象和性质密不可分.由图象想性质、由性质想图象.
(六)布置作业:
1.完成表格.
y=ax2 图象 (草图) 开口方向 顶点 对称轴 有最高或最低点 最值
a>0
a<0
2.教科书习题22.1巩固练习第3,4题.
五、目标检测设计
1.抛物线共有的性质是( ).
A.开口向上 B.对称轴都是轴 C.都有最高点 D.顶点都是原点
【设计意图】考查对二次函数的性质.
2.已知函数y=(m2-3m)的图象是抛物线,则函数的解析式为 ,抛物线的顶点坐标为______,对称轴为______,开口______.
【设计意图】由自变量的二次和的条件得到函数解析式,从解析式得到函数性质.
3.二次函数中,当时,与的大小关系是 .
【设计意图】考查对二次函数的增减性.
一、内容和内容解析
(一)内容
二次函数的图象和性质.
(二)内容解析
类比一次函数图象和性质的研究,采用从特殊函数到一般函数的研究方法.最简单二次函数的图象和性质,对a>0、a<0分别进行探究.通过用描点法在同一坐标系内画出的图象,引导学生观察这些函数图象的共同点和不同点,归纳得出二次函数的的图象和性质,同样类比研究的性质,最后从对称性、最值、增减性几个方面归纳出,体现了研究代数学问题的一般方法.
二、目标和目标解析
(一)教学目标
1.理解并掌握二次函数的图象和性质;
2.经历、探索二次函数图象性质的过程,学会研究函数性质的方法,培养观察、思考、归纳的良好思维习惯.
重点与难点:
重点:二次函数的图象和性质.
难点:数形结合探讨二次函数的图象和性质.
(二)目标解析
1.二次函数性质是由解析式和自变量取值范围决定的,所以从解析式分析得到函数图象的示意图和函数的性质,用图象来验证性质.
2.通过对多个函数图象的对比,发现共性,归纳函数的性质,帮助学生直观地理解二次函数的性质.
三、教学问题诊断分析
画二次函数的图象时学生容易出现的问题是点与点之间用折线连接,尤其在顶点附近部分图象画不好,可以让学生多画几对点,图象本身就是近似的,点取的越多越接近于标准.
本节课突出培养从特殊到一般、数形结合和类比思想解决问题,为学生学习后续函数、研究后续函数的图形和性质奠定扎实的基础.
本课的教学重点是理解二次函数的图象和性质,从解析式、表格、图象三种途径分别发现函数性质、理解函数性质.
本课的教学难点是二次函数的图象和性质的探究过程.
四、教学过程设计
(一)温故知新
1.回顾研究一次函数的基本方法:概念→图象和性质→应用性质.
2.按怎样的顺序研究一次函数的图象和性质?
令b=0,特殊的一次函数即正比例函数→b≠0的一次函数 ,可以通过正比例函数上下平移或左右平移得到即特殊→一般.
3.如何来研究二次函数的图形和性质呢?
引导学生仿照一次函数的研究方法,从特殊形式的二次函数入手,如:令时或令时或令时,从最简单、最特殊的形式开始研究,从而引出本节课的重点:探究二次函数的图象和性质.
师生活动:回忆一次函数的研究顺序,寻找最特殊的二次函数并入手研究二次函数的性质.
【设计意图】回顾一次函数的研究程序:概念→图象和性质→应用,类比研究二次函数的图象和性质.既巩固函数的研究方法,又引出今天学习的内容.
(二)合作交流,探究性质
1.从最简单的二次函数开始研究它的图象和性质.分a>0 和a<0,先研究a>0,并从a=1入手探究的图象和性质.
(1)从解析式研究函数的图象和性质.
从解析式研究下面的内容:
①自变量取值范围:x取全体实数;
②函数值y的取值范围:;
③当x取相反数时,函数y值相等;(对称性)
④当x=0时,y有最小值,y的最小值为0;
⑤当时,y随着x的增大而增大,当时,y随着x的增大而减小;
⑥图象分布于第一、二象限和原点;
⑦图象有最低点(0,0),图象在第一象限部分会是直线吗?不可能是直线,因为在第一象限部分,y随着x的增大不是匀速增大的,比如x=1时,y=1;当x=2时,y=4;当x=3时,y=9.x从1增加到2,y增加了3个单位,而x从2增加到3,y增加了5个单位,也就是说y不是匀速增大的而是有一个加速度的.所以它的图象在第一象限部分不是直线,而是曲线,并且y随着x的增大而增大.猜想二次函数在第一象限的示意图可能是如图1或如图2.
二次函数的示意图在第一象限部分示意图如图1还是如图2那样呢?图1是y的增长速度先慢后快,图2是先快后慢.比如取特殊点时,,y的增长速度先慢后快,可以判断图象应该如图1.
由前面第(3)条性质,当x取相反数时,函数y值相等,说明函数图象关于y轴对称,完整的示意图应该如图3.
归纳二次函数的性质:
图象关于y轴对称; 图象有最低点(0,0); 在y轴左侧,y随着x的增大而减小;在y轴右侧,y随着x的增大而增大.
师生活动:由解析式分析函数图象和性质,从自变量和函数值范围、对称性、增减性、最值等几个方面分析,得到函数性质和猜想函数示意图.
【设计意图】学会从函数解析式研究函数性质的方法,了解对一个新函数应该从哪些内容、按什么顺序研究它的性质,为探究函数性质的知识体系打下基础,并从中积累基本的数学活动经验.
(2)从表格研究函数的图象和性质.
为了得到准确的的图象,用描点法来画.
描点法的步骤是列表、描点、连线.列表时根据自变量的对称性取一些有代表性的对称点,由于时,,估计学生画图时会出现问题,建议在0到1之间多取几对数,如.
引导学生从表格发现二次函数的性质:
图象关于y轴对称; 图象有最低点(0,0);在y轴左侧,y随着x的增大而减小;在y轴右侧,y随着x的增大而增大.
学生在画图过程中容易出现点与点之间用折线连接,突破的办法就是多取几对点,尤其是自变量在0在1之间.
师生活动:用描点法画准确的的图象,先列表,取代表性的一些特殊值,从表格探究函数的性质.
【设计意图】从表格发现函数的图象和性质,从多种角度帮助学生理解函数的图象和性质,突出重点,突破难点,为学生后续研究函数性质奠定基础.
(3)从图象研究函数的性质.
用描点法得到y= x2的图象,给图象命名.二次函数y= x2的图象形状类似于投篮或掷铅球时球在空中所经过的路线,只是这条曲线开口向上,这条曲线叫抛物线y= x2.
二次函数的图象都是抛物线.
一般地,二次函数的图象叫做抛物线 .
抛物线y= x2关于y轴对称,y轴是它的对称轴.
对称轴与抛物线的交点叫做抛物线的顶点.
抛物线y= x2在x轴上方(除顶点外),顶点是它的最低点,开口向上,并且向上无限伸展; 当x=0时,函数 y的值最小,最小值是0.
在对称轴左侧(或x<0时),y随着x的增大而减小;
在对称轴右侧(或x>0时),y随着x的增大而增大.
师生活动:对照描点法画出的y= x2.的图象,给图象命名.在经历解析式、表格分析函数性质的基础上,归纳二次函数y= x2.的性质.
【设计意图】用描点法画出准确的图象验证猜想所得示意图,对照图象研究函数性质.从解析式、列表、图象三种函数表示法分别研究函数性质,帮助学生理解函数的性质.
2.从特殊到一般地归纳函数的图象和性质
画一画:在同一坐标系中画出下列函数的图象:y= x2 、y= 2x2 、y=x2、、、,并比较它们的相同点与不同点.
让学生讨论、交流,达成共识,当时,抛物线开口向上,在对称轴的左侧,抛物线自左向右下降;在对称轴的右侧,抛物线自左向右上升,顶点是抛物线上位置最低点.图象的这些特点,反映了当时,函数的性质;当时,函数值y随x的增大而减小;与时,函数值y随x的增大而增大,当时,函数值取得最小值,最小值是y=0.
当时,抛物线开口向下,在对称轴的左侧,抛物线自左向右上升;在对称轴的右侧,抛物线自左向右下降,顶点是抛物线上位置最高点.图象的这些特点,反映了当时,函数的性质;当x<0时,函数值y随x的增大而增大;与x>0时,函数值y随x的增大而减小,当x=0时,函数值取得最大值,最大值是y=0.
师生活动:在同一坐标系中画出不同的函数图象,合作交流,归纳二次函数的图象和性质.
【设计意图】通过对函数图象的画和分析,让学生一方面熟悉二次函数图象,见到二次函数想到抛物线,另一方面归纳总结的性质,渗透从特殊到一般的方法.对于a对抛物线开口大小的影响,教师还可以借助几何画板演示,多展示一些抛物线,给学生以直观的形象,进一步加深理解.
(三)新知应用,加深理解
例1 (1)抛物线的顶点坐标是 ,对称轴是 ,在 侧,y随着x的增大而增大;在 侧,y随着x的增大而减小,当 x= 时,函数 y的值最 ,最 值是 ,抛物线在x轴的 方(除顶点外).
(2)抛物线在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的 ,当x = 0时,函数y的值最 ,最 值是 ;当x 0时,y < 0.
师生活动:直接应用函数的图象和性质,二次函数的图象分两类,开口向上和向下.
【设计意图】巩固刚学的图象和性质,要求学生见解析式想图象.
例2 已知二次函数.
(1)当m取何值时,它的图象开口向下;
(2)当x>0时,y随x的增大而增大,求函数关系式.
师生活动:联系二次函数概念,直接考查函数的图象和性质.
【设计意图】建构新旧知识体系,要求学生从函数性质想图象.
(四)巩固概念,学以致用
巩固练习:教科书32页练习,增加一问:说出函数的增减性.
【设计意图】见函数想图象,数形结合,巩固二次函数的图象和性质.
(五)归纳小结,反思提高
不仅总结今天所学的知识,重点归纳数学方法和数学思维.
1.从函数解析式、表格、图象研究函数图象和性质的几个方面:自变量取值范围,函数值取值范围,对称性,最值,增减性等.
2.二次函数的图象和性质.
3.数形结合──图象和性质密不可分.由图象想性质、由性质想图象.
(六)布置作业:
1.完成表格.
y=ax2 图象 (草图) 开口方向 顶点 对称轴 有最高或最低点 最值
a>0
a<0
2.教科书习题22.1巩固练习第3,4题.
五、目标检测设计
1.抛物线共有的性质是( ).
A.开口向上 B.对称轴都是轴 C.都有最高点 D.顶点都是原点
【设计意图】考查对二次函数的性质.
2.已知函数y=(m2-3m)的图象是抛物线,则函数的解析式为 ,抛物线的顶点坐标为______,对称轴为______,开口______.
【设计意图】由自变量的二次和的条件得到函数解析式,从解析式得到函数性质.
3.二次函数中,当时,与的大小关系是 .
【设计意图】考查对二次函数的增减性.
同课章节目录
