2021-2022学年数学 人教A版(2019)必修第一册第四章 指数函数与对数函数 讲义
文档属性
| 名称 | 2021-2022学年数学 人教A版(2019)必修第一册第四章 指数函数与对数函数 讲义 |
|
|
| 格式 | docx | ||
| 文件大小 | 629.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 00:00:00 | ||
图片预览




文档简介
高一数学必修一专题:指数函数与对数函数
第一部分:指数函数与对数函数性质与图像
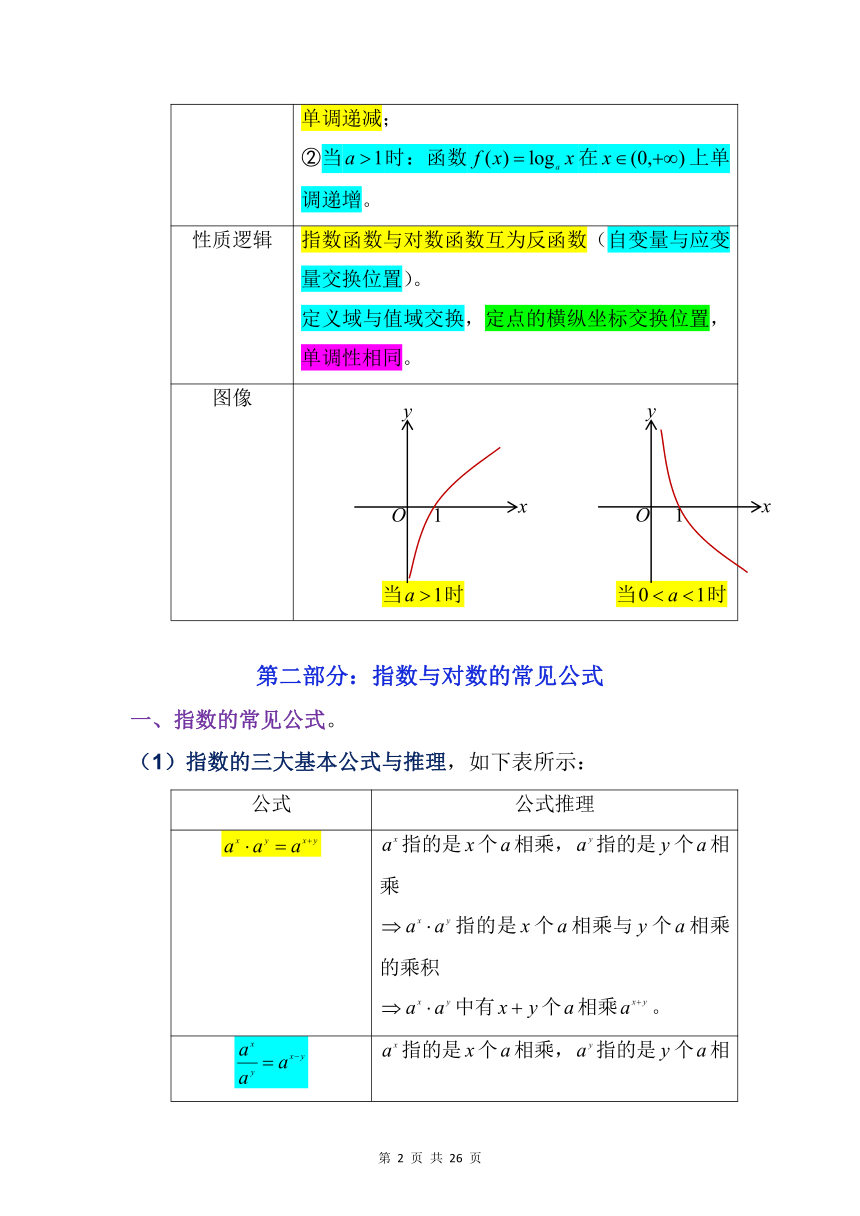
一、指数函数的图像与性质,如下表所示:
通式 指数函数通式:(且)
定义域、值域 ①定义域:;②值域:。
定点 指数函数一定过点(任何数的零次方都等于)
单调性 ①当时:函数在上单调递减; ②当时:函数在上单调递增。
图像 当时 当时
二、对数函数的图像与性质,如下表所示:
通式 对数函数的通式:(且)
定义域、值域 定义域:;值域:。
定点 对数函数一定过点(是任何数的零次方)
单调性 ①当时:函数在上单调递减; ②当时:函数在上单调递增。
性质逻辑 指数函数与对数函数互为反函数(自变量与应变量交换位置)。 定义域与值域交换,定点的横纵坐标交换位置,单调性相同。
图像 当时 当时
第二部分:指数与对数的常见公式
一、指数的常见公式。
(1)指数的三大基本公式与推理,如下表所示:
公式 公式推理
指的是个相乘,指的是个相乘 指的是个相乘与个相乘的乘积 中有个相乘。
指的是个相乘,指的是个相乘 指的是个相乘与个相乘的比值, 分子分母都约分掉个,分母消失,分子 剩余个相乘。
指的是个相乘,指的是个相乘 指的是个相乘。
(2)指数的三大其他公式与推理,如下表所示:
公式 公式推理
指的是个相乘,指的是个相乘 指的是个相乘与个相乘的乘积 中个相乘。
,分子有个相乘,分母有个相乘 ,一共有个相乘。
任何数的零次方等于。
二、对数的常见公式。
(1)对数的三大基本公式与推理,如下表所示:
公式 公式推理
假设:,。 方程左边。 方程右边。
假设:,。 方程左边。 方程右边。
假设:。 方程左边。 方程右边。
(2)对数的换底公式和推论与推理,如下表所示:
公式 公式推理
换底公式 假设:,。 方程左边。 方程右边。
根据换底公式得到:。
根据换底公式得到:, 。
① ② 底数与真数约分 根据换底公式得到:, 。
(3)对数的其他公式与推理,如下表所示:
公式 公式推理
。
假设:。。
第三部分:指数与对数的不等式
一、指数不等式的题型。
(1)指数不等式的题型解法,如下表所示:
指数不等式 解法设计
解不等式 解:第一种情况:当时:, 恒成立。 第二种情况:当时:,。 ①当时:函数在上单调递增。 函数值越大,自变量越大。 ②当时:函数在上单调递减。 函数值越大,自变量越小。
解不等式 解:第一种情况:当时:, 恒成立。 第二种情况:当时:,。 ①当时:函数在上单调递增。 函数值越大,自变量越大。 ②当时:函数在上单调递减。 函数值越大,自变量越小。
解不等式 解:第一种情况:当时:, 不成立(不等式不成立)。 第二种情况:当时:,。 ①当时:函数在上单调递增。 函数值越大,自变量越大。 ②当时:函数在上单调递减。 函数值越大,自变量越小。
解不等式 解:第一种情况:当时:, 不成立(不等式不成立)。 第二种情况:当时:,。 ①当时:函数在上单调递增。 函数值越大,自变量越大。 ②当时:函数在上单调递减。 函数值越大,自变量越小。
(2)指数不等式的例题讲解,如下表所示:
例题 解法设计
解不等式 解:恒成立。
解不等式 解: 。
解不等式 解: 。
解不等式 解:不成立(无解)。
解不等式 解:。
解不等式 解: ,。
(3)指数不等式的跟踪训练,如下表所示:
跟踪训练 解答区域
训练一:解不等式: 。 解:
训练二:解不等式: 。 解:
训练三:解不等式: 。 解:
训练四:解不等式: 。 解:
训练五:解不等式: 。 解:
训练六:解不等式: 。 解:
训练七:解不等式: 。 解:
训练八:解不等式: 。 解:
(4)指数不等式的跟踪训练参考答案,如下表所示:
训练一: 训练二:
训练三: 训练四:
训练五: 训练六:
训练七: 训练八:
二、对数不等式的题型。
(1)对数不等式的题型解法,如下表所示:
对数不等式 解法设计
解不等式 解:根据对数函数的真数大于零得到:。 ,。 ①当时:函数在上单调递减 ,。 ②当时:函数在上单调递增 ,。
解不等式 解:根据对数函数的真数大于零得到:。 ,。 ①当时:函数在上单调递减 ,。 ②当时:函数在上单调递增 ,。
解不等式 解:根据对数函数的真数大于零得到:。 ,。 ①当时:函数在上单调递减 ,。 ②当时:函数在上单调递增 ,。
解不等式 解:根据对数函数的真数大于零得到:。 ,。 ①当时:函数在上单调递减 ,。 ②当时:函数在上单调递增 ,。
(2)对数不等式的例题讲解,如下表所示:
例题 解法设计
解不等式 解:根据对数函数真数大于零得到:。 , ,。
解不等式 解:根据对数函数真数大于零得到:。 , , 。
解不等式 解:根据对数函数真数大于零得到:。 , ,。
解不等式 解:根据对数函数真数大于零得到:。 , ,。
(3)对数不等式的跟踪训练,如下表所示:
跟踪训练 解答区域
训练一:解不等式 解:
训练二:解不等式 解:
训练三:解不等式 解:
训练四:解不等式 解:
(4)对数不等式的跟踪训练参考答案,如下表所示:
训练一: 训练二:
训练三: 训练四:
第四部分:指数函数与对数函数的单调性
一、指数函数单调性的题型。
(1)指数函数单调性的题型原理,如下表所示:
题型 解法设计
题型一:判断:复合函数的单调性。 解:如下表所示: 的范围的范围单调性在上单调递增在上单调递减在上单调递减在上单调递增
题型二:判断:复合函数的单调性。 解:如下表所示: 的范围的正负单调性在上单调递减 在上单调递增在上单调递增 在上单调递减在上单调递增 在上单调递减在上单调递减 在上单调递增
题型三:判断:复合函数的单调性。 解:如下表所示: 的范围的范围单调性在上单调递增在上单调递减在上单调递减在上单调递增
题型四:判断:复合函数的单调性。 解:如下表所示: 的范围的范围单调性在上单调递增在上单调递减在上单调递减在上单调递增
(2)指数函数单调性的例题讲解,如下表所示:
例题 解法设计
例题一:判断:复合函数的单调性。 解:复合函数是由和组成。 在上单调递减,单调递减 复合函数在上单调递增。
例题二:判断:复合函数的单调性。 解:复合函数是由和组成。 的对称轴:。 ①在上单调递减; ②在上单调递增。 在定义域上单调递增。 所以:复合函数的单调性: ①在上单调递减; ②在上单调递增。
例题三:判断:复合函数的单调性。 解:复合函数是由和组成。 在上单调递减,单调递增 复合函数在上单调递减。
例题四:判断:复合函数的单调性。 解:复合函数是由和组成。 在单调递增;单调递减 复合函数在单调递减。
(3)指数函数单调性的跟踪训练,如下表所示:
跟踪训练 解答区域
训练一:判断:复合函数的单调性。 解:
训练二:判断:复合函数的单调性。 解:
训练三:判断:复合函数的单调性。 解:
训练四:判断:复合函数的单调性。 解:
(4)指数函数单调性的跟踪训练参考答案,如下表所示:
训练一:在上单调递减 训练二:在上单调递减 在上单调递增
训练三:在上单调递减 训练四:在上单调递增
二、对数函数单调性的题型。
(1)对数函数单调性的题型原理,如下表所示:
题型 解法设计
题型一:判断:复合函数 的单调性。 解:如下表所示: 的范围的正负的单调性在上单调递增在上单调递减在上单调递减在上单调递增
题型二:判断:复合函数 的单调性。 解:(1)当,时:如下表所示: 的范围的单调性在上单调递减 在上单调递增在上单调递增 在上单调递减
(2)当,时:如下表所示: 的范围的单调性在上单调递减 在上单调递增在上单调递增 在上单调递减
(3)当,时:如下表所示: 的范围的单调性在上单调递减 在上单调递增在上单调递增 在上单调递减
(4)当,时:如下表所示: 的范围的单调性在上单调递增 在上单调递减在上单调递减 在上单调递增
题型三:判断:复合函数的单调性。 解:如下表所示: 的范围的范围的单调性在上单调递增在上单调递减在上单调递减在上单调递增
题型四:判断:复合函数的单调性。 解:如下表所示: 的范围的范围的单调性在上单调递增在上单调递减在上单调递减在上单调递增
(2)对数函数单调性的例题讲解,如下表所示:
例题 解法设计
例题一:判断:复合函数的单调性。 解:定义域:。 复合函数是由和组成。 在上单调递增,单调递增 在上单调递增。
例题二:判断:复合函数的单调性。 解:定义域:。 复合函数是由和组成。在定义域区间上单调递减。 ①在上单调递减; ②在上单调递增。 所以:复合函数的单调性: ①在上单调递增; ②在上单调递减。
例题三:判断:复合函数的单调性。 解:定义域:。 复合函数是由和组成。 在上单调递增,单调递增。 所以:在上单调递增。
例题四:判断:复合函数的单调性。 解:定义域:。 是由和组成。 在上单调递减,单调递增 在上单调递减。
(3)对数函数单调性的跟踪训练,如下表所示:
跟踪训练 解答区域
训练一:判断:复合函数的单调性。
训练二:判断:复合函数的单调性。
训练三:判断:复合函数的单调性。
训练四:判断:复合函数的单调性。
训练五:判断:复合函数的单调性。
训练六:判断:复合函数的单调性。
训练七:判断:复合函数的单调性。
训练八:判断:复合函数的单调性。
(4)对数函数单调性的跟踪训练参考答案,如下表所示:
训练一:在上单调递增 训练二:在上单调递减
训练三:在上单调递减 在上单调递增 训练四:在上单调递增 在上单调递减
训练五:在上单调递增 在上单调递减 训练六:在上单调递增
训练七:在上单调递减 训练八:在上单调递减
第一部分:指数函数与对数函数性质与图像
一、指数函数的图像与性质,如下表所示:
通式 指数函数通式:(且)
定义域、值域 ①定义域:;②值域:。
定点 指数函数一定过点(任何数的零次方都等于)
单调性 ①当时:函数在上单调递减; ②当时:函数在上单调递增。
图像 当时 当时
二、对数函数的图像与性质,如下表所示:
通式 对数函数的通式:(且)
定义域、值域 定义域:;值域:。
定点 对数函数一定过点(是任何数的零次方)
单调性 ①当时:函数在上单调递减; ②当时:函数在上单调递增。
性质逻辑 指数函数与对数函数互为反函数(自变量与应变量交换位置)。 定义域与值域交换,定点的横纵坐标交换位置,单调性相同。
图像 当时 当时
第二部分:指数与对数的常见公式
一、指数的常见公式。
(1)指数的三大基本公式与推理,如下表所示:
公式 公式推理
指的是个相乘,指的是个相乘 指的是个相乘与个相乘的乘积 中有个相乘。
指的是个相乘,指的是个相乘 指的是个相乘与个相乘的比值, 分子分母都约分掉个,分母消失,分子 剩余个相乘。
指的是个相乘,指的是个相乘 指的是个相乘。
(2)指数的三大其他公式与推理,如下表所示:
公式 公式推理
指的是个相乘,指的是个相乘 指的是个相乘与个相乘的乘积 中个相乘。
,分子有个相乘,分母有个相乘 ,一共有个相乘。
任何数的零次方等于。
二、对数的常见公式。
(1)对数的三大基本公式与推理,如下表所示:
公式 公式推理
假设:,。 方程左边。 方程右边。
假设:,。 方程左边。 方程右边。
假设:。 方程左边。 方程右边。
(2)对数的换底公式和推论与推理,如下表所示:
公式 公式推理
换底公式 假设:,。 方程左边。 方程右边。
根据换底公式得到:。
根据换底公式得到:, 。
① ② 底数与真数约分 根据换底公式得到:, 。
(3)对数的其他公式与推理,如下表所示:
公式 公式推理
。
假设:。。
第三部分:指数与对数的不等式
一、指数不等式的题型。
(1)指数不等式的题型解法,如下表所示:
指数不等式 解法设计
解不等式 解:第一种情况:当时:, 恒成立。 第二种情况:当时:,。 ①当时:函数在上单调递增。 函数值越大,自变量越大。 ②当时:函数在上单调递减。 函数值越大,自变量越小。
解不等式 解:第一种情况:当时:, 恒成立。 第二种情况:当时:,。 ①当时:函数在上单调递增。 函数值越大,自变量越大。 ②当时:函数在上单调递减。 函数值越大,自变量越小。
解不等式 解:第一种情况:当时:, 不成立(不等式不成立)。 第二种情况:当时:,。 ①当时:函数在上单调递增。 函数值越大,自变量越大。 ②当时:函数在上单调递减。 函数值越大,自变量越小。
解不等式 解:第一种情况:当时:, 不成立(不等式不成立)。 第二种情况:当时:,。 ①当时:函数在上单调递增。 函数值越大,自变量越大。 ②当时:函数在上单调递减。 函数值越大,自变量越小。
(2)指数不等式的例题讲解,如下表所示:
例题 解法设计
解不等式 解:恒成立。
解不等式 解: 。
解不等式 解: 。
解不等式 解:不成立(无解)。
解不等式 解:。
解不等式 解: ,。
(3)指数不等式的跟踪训练,如下表所示:
跟踪训练 解答区域
训练一:解不等式: 。 解:
训练二:解不等式: 。 解:
训练三:解不等式: 。 解:
训练四:解不等式: 。 解:
训练五:解不等式: 。 解:
训练六:解不等式: 。 解:
训练七:解不等式: 。 解:
训练八:解不等式: 。 解:
(4)指数不等式的跟踪训练参考答案,如下表所示:
训练一: 训练二:
训练三: 训练四:
训练五: 训练六:
训练七: 训练八:
二、对数不等式的题型。
(1)对数不等式的题型解法,如下表所示:
对数不等式 解法设计
解不等式 解:根据对数函数的真数大于零得到:。 ,。 ①当时:函数在上单调递减 ,。 ②当时:函数在上单调递增 ,。
解不等式 解:根据对数函数的真数大于零得到:。 ,。 ①当时:函数在上单调递减 ,。 ②当时:函数在上单调递增 ,。
解不等式 解:根据对数函数的真数大于零得到:。 ,。 ①当时:函数在上单调递减 ,。 ②当时:函数在上单调递增 ,。
解不等式 解:根据对数函数的真数大于零得到:。 ,。 ①当时:函数在上单调递减 ,。 ②当时:函数在上单调递增 ,。
(2)对数不等式的例题讲解,如下表所示:
例题 解法设计
解不等式 解:根据对数函数真数大于零得到:。 , ,。
解不等式 解:根据对数函数真数大于零得到:。 , , 。
解不等式 解:根据对数函数真数大于零得到:。 , ,。
解不等式 解:根据对数函数真数大于零得到:。 , ,。
(3)对数不等式的跟踪训练,如下表所示:
跟踪训练 解答区域
训练一:解不等式 解:
训练二:解不等式 解:
训练三:解不等式 解:
训练四:解不等式 解:
(4)对数不等式的跟踪训练参考答案,如下表所示:
训练一: 训练二:
训练三: 训练四:
第四部分:指数函数与对数函数的单调性
一、指数函数单调性的题型。
(1)指数函数单调性的题型原理,如下表所示:
题型 解法设计
题型一:判断:复合函数的单调性。 解:如下表所示: 的范围的范围单调性在上单调递增在上单调递减在上单调递减在上单调递增
题型二:判断:复合函数的单调性。 解:如下表所示: 的范围的正负单调性在上单调递减 在上单调递增在上单调递增 在上单调递减在上单调递增 在上单调递减在上单调递减 在上单调递增
题型三:判断:复合函数的单调性。 解:如下表所示: 的范围的范围单调性在上单调递增在上单调递减在上单调递减在上单调递增
题型四:判断:复合函数的单调性。 解:如下表所示: 的范围的范围单调性在上单调递增在上单调递减在上单调递减在上单调递增
(2)指数函数单调性的例题讲解,如下表所示:
例题 解法设计
例题一:判断:复合函数的单调性。 解:复合函数是由和组成。 在上单调递减,单调递减 复合函数在上单调递增。
例题二:判断:复合函数的单调性。 解:复合函数是由和组成。 的对称轴:。 ①在上单调递减; ②在上单调递增。 在定义域上单调递增。 所以:复合函数的单调性: ①在上单调递减; ②在上单调递增。
例题三:判断:复合函数的单调性。 解:复合函数是由和组成。 在上单调递减,单调递增 复合函数在上单调递减。
例题四:判断:复合函数的单调性。 解:复合函数是由和组成。 在单调递增;单调递减 复合函数在单调递减。
(3)指数函数单调性的跟踪训练,如下表所示:
跟踪训练 解答区域
训练一:判断:复合函数的单调性。 解:
训练二:判断:复合函数的单调性。 解:
训练三:判断:复合函数的单调性。 解:
训练四:判断:复合函数的单调性。 解:
(4)指数函数单调性的跟踪训练参考答案,如下表所示:
训练一:在上单调递减 训练二:在上单调递减 在上单调递增
训练三:在上单调递减 训练四:在上单调递增
二、对数函数单调性的题型。
(1)对数函数单调性的题型原理,如下表所示:
题型 解法设计
题型一:判断:复合函数 的单调性。 解:如下表所示: 的范围的正负的单调性在上单调递增在上单调递减在上单调递减在上单调递增
题型二:判断:复合函数 的单调性。 解:(1)当,时:如下表所示: 的范围的单调性在上单调递减 在上单调递增在上单调递增 在上单调递减
(2)当,时:如下表所示: 的范围的单调性在上单调递减 在上单调递增在上单调递增 在上单调递减
(3)当,时:如下表所示: 的范围的单调性在上单调递减 在上单调递增在上单调递增 在上单调递减
(4)当,时:如下表所示: 的范围的单调性在上单调递增 在上单调递减在上单调递减 在上单调递增
题型三:判断:复合函数的单调性。 解:如下表所示: 的范围的范围的单调性在上单调递增在上单调递减在上单调递减在上单调递增
题型四:判断:复合函数的单调性。 解:如下表所示: 的范围的范围的单调性在上单调递增在上单调递减在上单调递减在上单调递增
(2)对数函数单调性的例题讲解,如下表所示:
例题 解法设计
例题一:判断:复合函数的单调性。 解:定义域:。 复合函数是由和组成。 在上单调递增,单调递增 在上单调递增。
例题二:判断:复合函数的单调性。 解:定义域:。 复合函数是由和组成。在定义域区间上单调递减。 ①在上单调递减; ②在上单调递增。 所以:复合函数的单调性: ①在上单调递增; ②在上单调递减。
例题三:判断:复合函数的单调性。 解:定义域:。 复合函数是由和组成。 在上单调递增,单调递增。 所以:在上单调递增。
例题四:判断:复合函数的单调性。 解:定义域:。 是由和组成。 在上单调递减,单调递增 在上单调递减。
(3)对数函数单调性的跟踪训练,如下表所示:
跟踪训练 解答区域
训练一:判断:复合函数的单调性。
训练二:判断:复合函数的单调性。
训练三:判断:复合函数的单调性。
训练四:判断:复合函数的单调性。
训练五:判断:复合函数的单调性。
训练六:判断:复合函数的单调性。
训练七:判断:复合函数的单调性。
训练八:判断:复合函数的单调性。
(4)对数函数单调性的跟踪训练参考答案,如下表所示:
训练一:在上单调递增 训练二:在上单调递减
训练三:在上单调递减 在上单调递增 训练四:在上单调递增 在上单调递减
训练五:在上单调递增 在上单调递减 训练六:在上单调递增
训练七:在上单调递减 训练八:在上单调递减
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
