6.1习题课:圆周运动的描述 课件(共20张PPT)
文档属性
| 名称 | 6.1习题课:圆周运动的描述 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 839.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-08 21:25:46 | ||
图片预览







文档简介
(共20张PPT)
Me
ercu
aeydoson
在图5.5-3中,设物体做圆周运动的半径为r,由A运动到B的时间为△t,AB弧长为
△,AB弧对应的园心角为△0。当△以弧度为单位时,△=4
△l=r△
由于△l=At,△=OMt,代入上式后得到
0=r
(3)
这表明,在圆周运动中,线速度的大小等于角速度大小与半径的乘积。
B
O
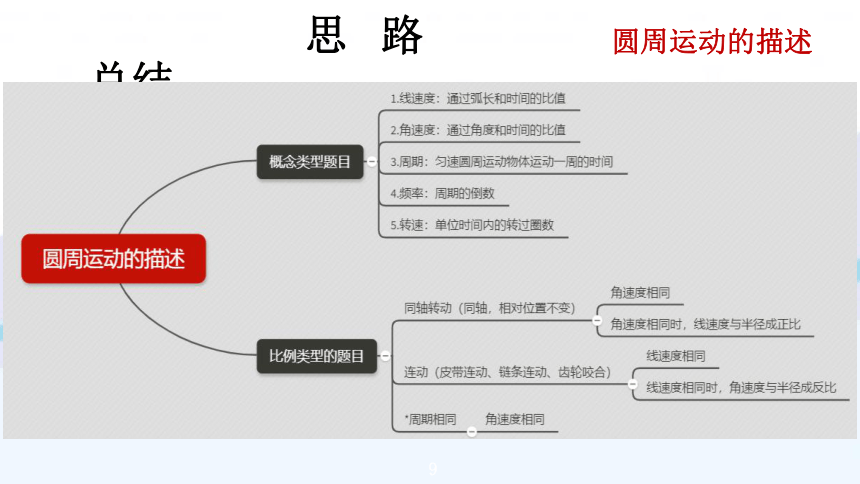
1线速度:通过弧长和时间的比值
2角速度:通过角度和时间的比值
概念类型题I
3周期:匀速圆周运动物体运动一周的时间
4频率:周期的倒数
5转速:单位时间内的转过圈数
圆周运动的描述
角速度相同
同轴转动(同轴,相对位置不变)
角速度相同时,线速度与半径成正比
比例类型的题
线速度相同
连动(皮带连动、链条连动、齿轮咬合)
线速度相同时,角速度与半径成反比
周期相同角速度相同
△
B
乙
图56-3质点从A运动到B的速度变化量
定义
指向圆心的加速度只改变线速度方向,不影响大小
若实际加速度指向圆心即可称为物体运动的向心加速度速度大小不变
径向分量改变线速度方向
与实际加速度区分
向心加速度
若实际加速度不指向圆心切向分量改变线速度大小
速度大小发生变化
4丌
匀速圆周运动的向心加速度的种表达方式
a
27
1判断物体的运动情况(是否有周期性)
圆周运动周期性问题
2找到两个运动物体间的联系
运动时间t
3根据匀速圆周运动的周期性解决问题=1t△tn△tT
Me
ercu
aeydoson
在图5.5-3中,设物体做圆周运动的半径为r,由A运动到B的时间为△t,AB弧长为
△,AB弧对应的园心角为△0。当△以弧度为单位时,△=4
△l=r△
由于△l=At,△=OMt,代入上式后得到
0=r
(3)
这表明,在圆周运动中,线速度的大小等于角速度大小与半径的乘积。
B
O
1线速度:通过弧长和时间的比值
2角速度:通过角度和时间的比值
概念类型题I
3周期:匀速圆周运动物体运动一周的时间
4频率:周期的倒数
5转速:单位时间内的转过圈数
圆周运动的描述
角速度相同
同轴转动(同轴,相对位置不变)
角速度相同时,线速度与半径成正比
比例类型的题
线速度相同
连动(皮带连动、链条连动、齿轮咬合)
线速度相同时,角速度与半径成反比
周期相同角速度相同
△
B
乙
图56-3质点从A运动到B的速度变化量
定义
指向圆心的加速度只改变线速度方向,不影响大小
若实际加速度指向圆心即可称为物体运动的向心加速度速度大小不变
径向分量改变线速度方向
与实际加速度区分
向心加速度
若实际加速度不指向圆心切向分量改变线速度大小
速度大小发生变化
4丌
匀速圆周运动的向心加速度的种表达方式
a
27
1判断物体的运动情况(是否有周期性)
圆周运动周期性问题
2找到两个运动物体间的联系
运动时间t
3根据匀速圆周运动的周期性解决问题=1t△tn△tT
