第十二章 全等三角形 综合复习大全(含解析)
文档属性
| 名称 | 第十二章 全等三角形 综合复习大全(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
全等三角形综合复习大全
知识梳理
三角形全等的判定一
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.
三角形全等的判定二
有两边和它们的夹角对应相等的两个三角形全等(简称“边角边”或“SAS”)
三角形全等的判定三
两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
三角形全等的判定四
两个角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”).
三角形全等的判定五
斜边与一直角边对应相等的两个直角三角形全等.(HL)
特别注意:全等三角形的判定中没有边边角定理,即不存在SSA定理
角平分线的性质定理:角平分线上的点到角两边的距离相等。
角平分线的判定定理:到一个角的两边的距离相等的点,在这个角的平分线上。
巩固练习
一.全等三角形的性质(共2小题)
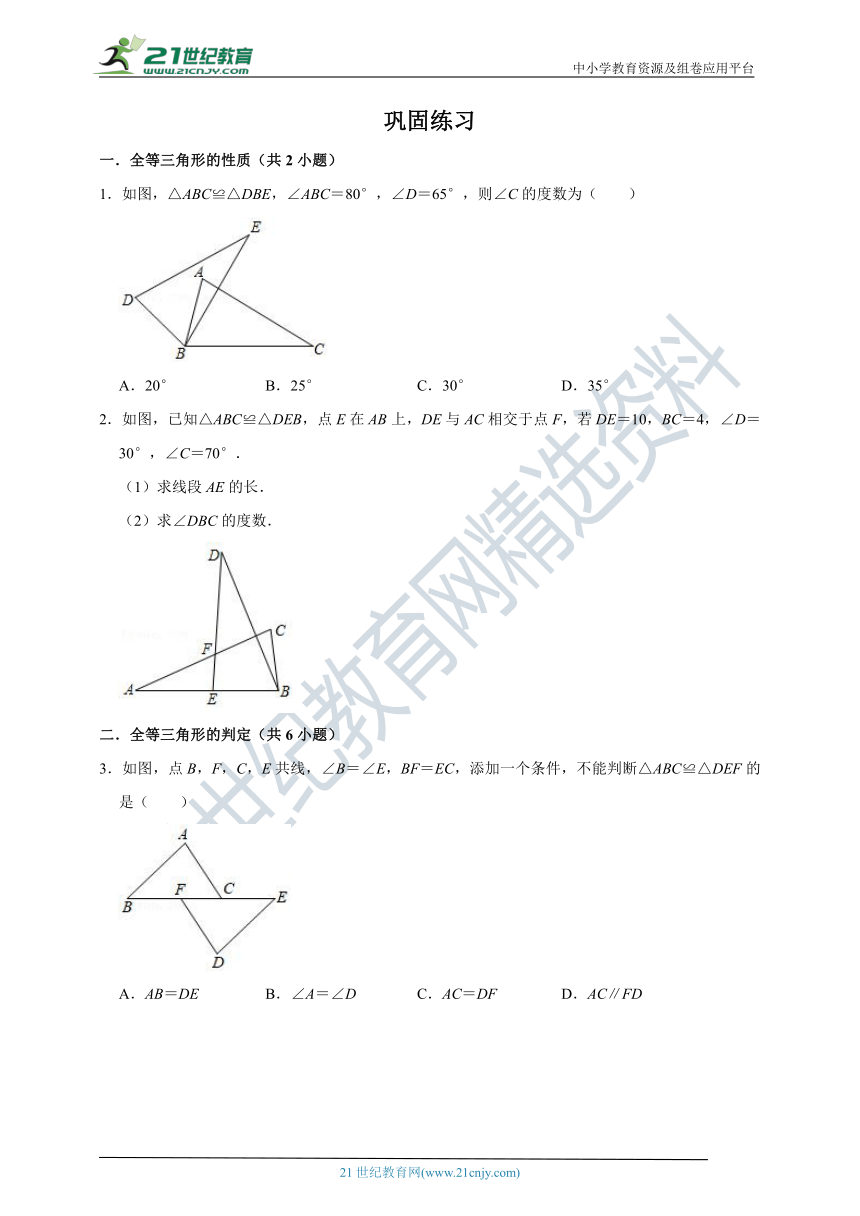
1.如图,△ABC≌△DBE,∠ABC=80°,∠D=65°,则∠C的度数为( )
A.20° B.25° C.30° D.35°
2.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
二.全等三角形的判定(共6小题)
3.如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠A=∠D C.AC=DF D.AC∥FD
4.如图,在△ABC和△DCB中,∠ACB=∠DBC,添加一个条件,不能证明△ABC和△DCB全等的是( )
A.∠ABC=∠DCB B.AB=DC C.AC=DB D.∠A=∠D
5.如图,已知AD=AE,∠B=∠C.求证:△ACD≌△ABE.
6.如图,点A、F、C、D在同一各直线上.AB∥DE.AB=DE,AF=DC.求证:△ABC≌△DEF.
7.如图,在△ABC和△DEF中,边AC,DE交于点H,AB∥DE,AB=DE,BE=CF.
(1)若∠B=55°,∠ACB=100°,求∠CHE的度数.
(2)求证:△ABC≌△DEF.
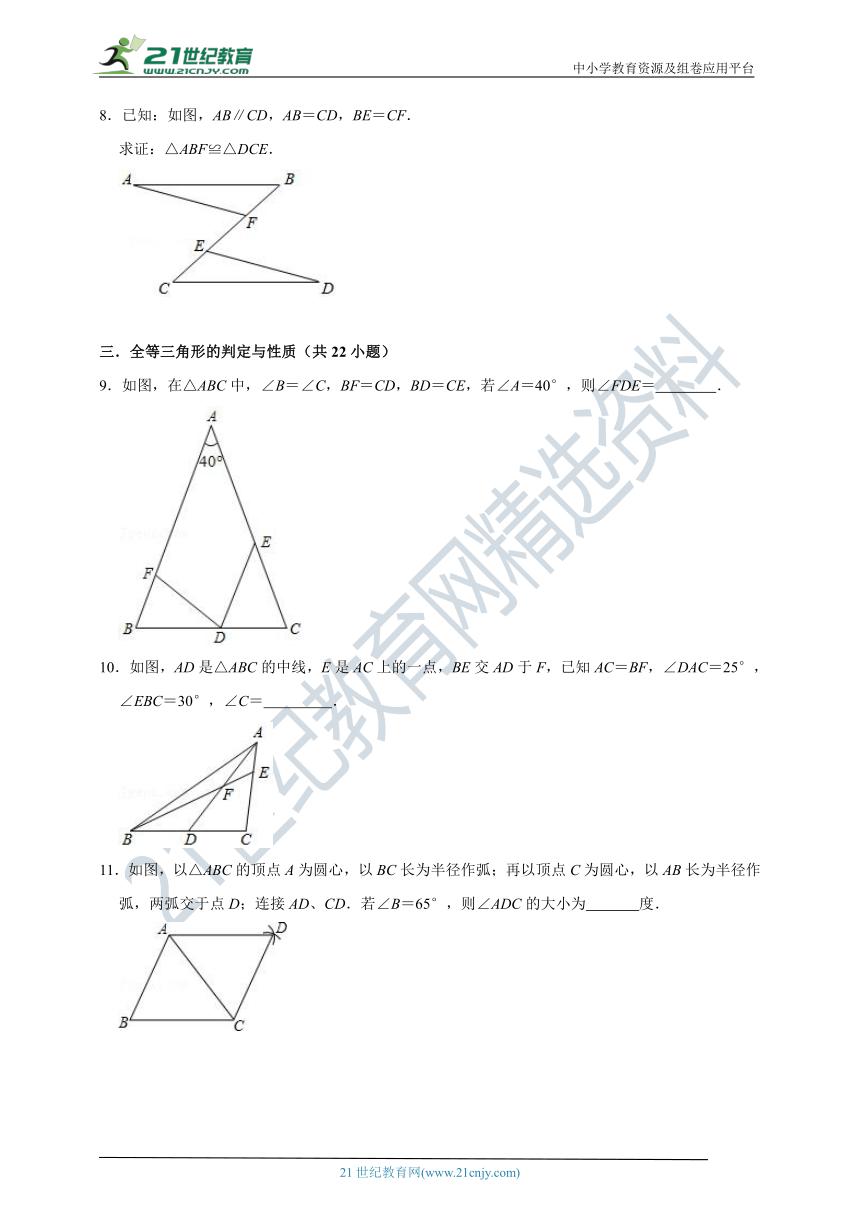
8.已知:如图,AB∥CD,AB=CD,BE=CF.
求证:△ABF≌△DCE.
三.全等三角形的判定与性质(共22小题)
9.如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,若∠A=40°,则∠FDE= .
10.如图,AD是△ABC的中线,E是AC上的一点,BE交AD于F,已知AC=BF,∠DAC=25°,∠EBC=30°,∠C= .
11.如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连接AD、CD.若∠B=65°,则∠ADC的大小为 度.
12.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:AD+DE=BC;
(2)若∠BDC=70°,求∠ADB的度数.
13.如图,在△ABC中,AB=AC,D是边BC延长线上一点,连接AD,过A做AE=AD,且∠DAE=∠BAC,连接CE交AD于点F.
(1)求证:△ABD≌△ACE;
(2)若∠FCD=34°,求∠B的度数.
14.如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于E点,DE=EF.
(1)求证:△ADE≌△CFE;
(2)若AB=5,CF=4,求BD的长.
15.如图,在△ABC中,D是边BC上的点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF,CE=BF.求证:∠B=∠C.
16.如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)求∠EAF的度数.
17.如图,在四边形ABCD中,AB∥CD,连接BD,点E在BD上,连接CE,若∠1=∠2,AB=ED,求证:DB=CD.
18.如图,AC∥BD,∠C=90°,AC=BE,AB=DE,求证:DE⊥AB.
19.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,BE,AD相交于点F,BF=AC.
(1)求证:△BDF≌△ADC.
(2)若AF=1,DC=2,求AB的长.
20.如图,BE⊥AE,CF⊥AE,垂足分别为E、F,D是EF的中点,CF=AF.
(1)请说明CD=BD;
(2)若BE=6,DE=3,请直接写出△ACD的面积.
21.如图,点D、E、F、B在同一直线上,DE=BF,CE=AF,EC∥AF.
(1)求证:AB=CD;
(2)若∠A=30°,∠D=40°,求∠DEC的度数.
22.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.
(1)求证:△ABD≌△EDC;
(2)若AB=2,BE=3,求CD的长.
23.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.
(1)求证:△ABE≌△CDF;
(2)连接BC,若∠CFD=100°,∠BCE=30°,求∠CBE的度数.
24.如图,在△ABC中,点D,E,F分别在AB,BC,AC上,∠B=∠C=∠DEF=60°,BD=CE.
(1)求证:∠BDE=∠CEF;
(2)若DE=3,求EF的长.
25.如图,已知△ABC和△CDE均是直角三角形,∠ACB=∠CED=90°,AC=CE,AB⊥CD于点F.
(1)求证:△ABC≌△CDE;
(2)若点B是EC的中点,DE=10cm,求AE的长.
26.如图,AD⊥CD,BC⊥CD,∠AED=∠EBC,AD=CE,求证:AE=EB.
27.如图,△ABC中,AB=AC,AD是BC边上的高,CE是AB边上的高,AE=CE.
求证:(1)△AEF≌△CEB;
(2)AF=2CD.
28.如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,E是对角线AC上一点,连接BE,DE.
(1)求证:BE=DE.
(2)当BE∥CD,∠BAD=78°时,求∠BED的度数.
29.如图,已知AB=AC,CD⊥AB,BE⊥AC,垂足分别为点D、E.求证:BD=CE.
30.已知:如图,AB=DC,AC=DB,AC和BD相交于点O.点E是BC的中点,连接OE.
(1)求证:△ABC≌△DCB;
(2)求∠BEO的度数.
四.角平分线的性质(共11小题)
31.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.8 B.7.5 C.15 D.无法确定
32.如图,已知△ABC中,∠C=90o,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,且AB=10,则△DEB的周长为( )
A.9 B.5 C.10 D.不能确定
33.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D,DE=3cm,那么CE等于( )
A.cm B.2cm C.3cm D.4cm
34.如图,三条公路两两相交,现计划修建一个油库,计划使得该油库到三条公路的距离相等,则油库的可选位置有( )处.
A.1 B.2 C.3 D.4
35.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,BC=10cm,点D到AB的距离为4cm,则DB=( )
A.6cm B.8cm C.5cm D.4cm
36.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=9.6cm,则D到AB的距离为( )
A.2.2cm B.3.2cm C.4.8cm D.6.4cm
37.如图,AD是△ABC的角平分线,DF⊥AB于点F,且DE=DG,S△ADG=24,S△AED=18,则△DEF的面积为( )
A.2 B.3 C.4 D.6
38.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=18,S△ABD=27,则CD的长为( )
A.4 B.8 C.3 D.6
39.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF⊥AB,交AB于点F,交BE于点D,若BC=8cm,DF=3cm,则△CDB的面积为( )
A.12cm2 B.8cm2 C.6cm2 D.4cm2
40.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是152cm2,AB=20cm,AC=18cm,求DE的长.
41.如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长.
全等三角形
参考答案与试题解析
一.全等三角形的性质(共2小题)
1.如图,△ABC≌△DBE,∠ABC=80°,∠D=65°,则∠C的度数为( )
A.20° B.25° C.30° D.35°
【分析】根据全等三角形的对应角相等得到∠DBE=∠ABC,根据三角形内角和定理计算,得到答案.
【解答】解:∵△ABC≌△DBE,∠ABC=80°,
∴∠DBE=∠ABC=80°,
∵∠D=65°,
∴∠C=180°﹣∠DBE﹣∠D=35°,
故选:D.
2.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
【分析】(1)根据全等三角形的性质得到AB=DE=10,BE=BC=4,结合图形计算,得到答案;
(2)根据全等三角形的性质得到∠BAC=∠D=30°,∠DBE=∠C=70°,根据三角形内角和定理求出∠ABC,计算即可.
【解答】解:(1)∵△ABC≌△DEB,DE=10,BC=4,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠C=70°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
二.全等三角形的判定(共6小题)
3.如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠A=∠D C.AC=DF D.AC∥FD
【分析】根据全等三角形的判定方法,可以判断添加各个选项中的条件是否能够判断△ABC≌△DEF,本题得以解决.
【解答】解:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
又∵∠B=∠E,
∴当添加条件AB=DE时,△ABC≌△DEF(SAS),故选项A不符合题意;
当添加条件∠A=∠D时,△ABC≌△DEF(AAS),故选项B不符合题意;
当添加条件AC=DF时,无法判断△ABC≌△DEF,故选项C符合题意;
当添加条件AC∥FD时,则∠ACB=∠DFE,故△ABC≌△DEF(ASA),故选项D不符合题意;
故选:C.
4.如图,在△ABC和△DCB中,∠ACB=∠DBC,添加一个条件,不能证明△ABC和△DCB全等的是( )
A.∠ABC=∠DCB B.AB=DC C.AC=DB D.∠A=∠D
【分析】根据证明三角形全等的条件AAS,SAS,ASA,SSS逐一验证选项即可.
【解答】解:在△ABC和△DCB中,
∵∠ACB=∠DBC,BC=BC,
A:当∠ABC=∠DCB时,△ABC≌△DCB(ASA),
故A能证明;
B:当AB=DC时,不能证明两三角形全等,
故B不能证明;
C:当AC=DB时,△ABC≌△DCB(SAS),
故C能证明;
D:当∠A=∠D时,△ABC≌△DCB(AAS),
故D能证明;
故选:B.
5.如图,已知AD=AE,∠B=∠C.求证:△ACD≌△ABE.
【分析】根据题目中的条件,利用AAS可以证明△ACD≌△ABE.
【解答】证明:在△ACD和△ABE中,
,
∴△ACD≌△ABE(AAS).
6.如图,点A、F、C、D在同一各直线上.AB∥DE.AB=DE,AF=DC.求证:△ABC≌△DEF.
【分析】根据平行线的性质得出∠A=∠D,求出AC=DF,再根据全等三角形的判定定理推出即可.
【解答】证明:∵AB∥DE,
∴∠A=∠D,
∵AF=DC,
∴AF+CF=DC+CF,
即AC=DF,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
7.如图,在△ABC和△DEF中,边AC,DE交于点H,AB∥DE,AB=DE,BE=CF.
(1)若∠B=55°,∠ACB=100°,求∠CHE的度数.
(2)求证:△ABC≌△DEF.
【分析】(1)根据三角形内角和定理求出∠A,再根据平行线的性质得出∠CHE=∠A即可;
(2)根据平行线的性质得出∠B=∠DEF,求出BC=EF,再根据全等三角形的判定定理推出即可.
【解答】(1)解:∵∠B=55°,∠ACB=100°,
∴∠A=180°﹣∠B﹣∠ACB=25°,
∵AB∥DE,
∴∠CHE=∠A=25°;
(2)证明:∵AB∥DE,
∴∠B=∠DEF,
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
8.已知:如图,AB∥CD,AB=CD,BE=CF.
求证:△ABF≌△DCE.
【分析】根据BE=CF求出BF=CE,根据平行线的性质得出∠B=∠C,再根据全等三角形的判定定理推出即可.
【解答】证明:∵BE=CF,
∴BE﹣EF=CF﹣EF,
即BF=CE,
∵AB∥CD,
∴∠B=∠C,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(SAS).
三.全等三角形的判定与性质(共22小题)
9.如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,若∠A=40°,则∠FDE= 70° .
【分析】根据全等三角形的判定推出△BFD≌△CDE,根据全等三角形的性质得出∠BFD=∠CDE,根据三角形的内角和定理求出∠B=∠C=(180°﹣∠A)=70°,求出∠FDB+∠EDC=∠FDB+∠BFD=180°﹣∠B=110°,再求出答案即可.
【解答】解:在△BFD和△CDE中,
,
∴△BFD≌△CDE(SAS),
∴∠BFD=∠CDE,
∵∠B=∠C,∠A=40°,
∴∠B=∠C=(180°﹣∠A)=70°,
∴∠FDB+∠CDE=∠FDB+∠BFD=180°﹣∠B=110°,
∴∠FDE=180°﹣(∠FDB+∠EDC)=180°﹣110°=70°,
故答案为:70°.
10.如图,AD是△ABC的中线,E是AC上的一点,BE交AD于F,已知AC=BF,∠DAC=25°,∠EBC=30°,∠C= 100° .
【分析】延长AD到M,使得DM=AD,连接BM,证△BDM≌△CDA(SAS),得BM=AC=BF,∠M=∠DAC=25°,∠C=∠DBM,再证△BFM是等腰三角形,求出∠MBF的度数,即可解决问题.
【解答】解:如图,延长AD到M,使得DM=AD,连接BM,如图所示:
在△BDM和△CDA中,
,
∴△BDM≌△CDA(SAS),
∴BM=AC=BF,∠M=∠DAC=25°,∠C=∠DBM,
∵BF=AC,
∴BF=BM,
∴∠M=∠BFM=25°,
∴∠MBF=180°﹣∠M﹣∠BFM=130°,
∵∠EBC=30°,
∴∠DBM=∠MBF﹣∠EBC=100°,
∴∠C=∠DBM=100°,
故答案为:100°.
11.如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连接AD、CD.若∠B=65°,则∠ADC的大小为 65 度.
【分析】根据作法可得AB=CD,BC=AD,然后利用“边边边”证明△ABC和△CDA全等,再根据全等三角形对应角相等解答.
【解答】解:∵以点A为圆心,以BC长为半径作弧;以顶点C为圆心,以AB长为半径作弧,两弧交于点D,
∴AB=CD,BC=AD,
在△ABC和△CDA中,
,
∴△ABC≌△CDA(SSS),
∴∠ADC=∠B=65°.
故答案为:65.
12.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:AD+DE=BC;
(2)若∠BDC=70°,求∠ADB的度数.
【分析】(1)由“ASA”可证△ADB≌△EBC,可得BC=BD,可得结论;
(2)由等腰三角形的性质可得∠BDC=∠BCD=70°,即可求解.
【解答】证明:(1)∵AD∥BC,
∴∠ADB=∠CBE,
在△ADB和△EBC中,
,
∴△ADB≌△EBC(ASA),
∴BC=BD,
∵BE+DE=DB,
∴AD+DE=BC;
(2)∵BC=BD,
∴∠BDC=∠BCD=70°,
∴∠DBC=40°,
∴∠ADB=40°.
13.如图,在△ABC中,AB=AC,D是边BC延长线上一点,连接AD,过A做AE=AD,且∠DAE=∠BAC,连接CE交AD于点F.
(1)求证:△ABD≌△ACE;
(2)若∠FCD=34°,求∠B的度数.
【分析】(1)根据题意AB=AC、AE=AD,只需证明其对应两边的夹角相等即可证明△ABD≌△ACE;
(2)根据图形得出∠ACB+ACE+∠FCE=180°,将相等的角代入求解即可.
【解答】(1)证明:∵∠DAE=∠BAC,
∴∠DAE+∠DAC=∠BAC+∠DAC,即∠EAC=∠DAB,
在△ABD和△ACE中,
,
∴△ABD∽△ACE(SAS).
(2)由(1)可知∠B=∠ACB=ACE,
∵∠ACB+ACE+∠FCE=180°,
即2∠B+34°=180°,
∴∠B=73°.
14.如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于E点,DE=EF.
(1)求证:△ADE≌△CFE;
(2)若AB=5,CF=4,求BD的长.
【分析】(1)利用角角边定理判定即可;
(2)利用全等三角形对应边相等可得AD的长,用AB﹣AD即可得出结论.
【解答】(1)证明:∵CF∥AB,
∴∠ADF=∠F,∠A=∠ECF.
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS).
(2)∵△ADE≌△CFE,
∴AD=CF=4.
∴BD=AB﹣AD=5﹣4=1.
15.如图,在△ABC中,D是边BC上的点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF,CE=BF.求证:∠B=∠C.
【分析】由垂直的定义,DE=DF,CE=BF证明△BDF≌△CDE,得出对应角相等即可.
【解答】证明:∵DE⊥AC,DF⊥AB,
∴∠BFD=∠CED=90°,
在△BDF和△CDE中,
,
∴△BDF≌△CDE(SAS),
∴∠B=∠C.
16.如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)求∠EAF的度数.
【分析】(1)利用SAS证明△AEB≌△FAC可证明结论;
(2)由全等三角形的性质可得∠E=∠CAF,由余角的定义可求得∠EAF的度数.
【解答】(1)证明:∵CD⊥AB,BE⊥AC,
∴∠CAD+∠ACD=∠CAD+∠EBA=90°,
∴∠ACD=∠EBA,
在△AEB和△FAC中,
,
∴△AEB≌△FAC(SAS),
∴AE=FA;
(2)解:∵△AEB≌△FAC,
∴∠E=∠CAF,
∵∠E+∠EAG=90°,
∴∠CAF+∠EAG=90°,
即∠EAF=90°.
17.如图,在四边形ABCD中,AB∥CD,连接BD,点E在BD上,连接CE,若∠1=∠2,AB=ED,求证:DB=CD.
【分析】根据AB∥CD,可得∠ABD=∠EDC,利用AAS证明△ABD≌△EDC,即可得结论.
【解答】证明:∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
∴DB=CD.
18.如图,AC∥BD,∠C=90°,AC=BE,AB=DE,求证:DE⊥AB.
【分析】先根据平行线的性质求出∠DBE=∠C=90°,再由HL定理可判定△ACB≌△EBD,由全等三角形的性质解答即可.
【解答】证明:设AB与DE相交于点M,
∵AC∥BD,
∴∠C+∠DBE=180°,
∵∠C=90°,
∴∠DBE=90°,
在Rt△ACB与Rt△EBD中,
,
∴Rt△ACB≌Rt△EBD(HL),
∴∠ABC=∠D,
∵∠D+∠MEB=90°,
∴∠ABC+∠MEB=90°,
∴∠EMB=180°﹣∠ABC﹣∠MEB=90°,
∴DE⊥AB.
19.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,BE,AD相交于点F,BF=AC.
(1)求证:△BDF≌△ADC.
(2)若AF=1,DC=2,求AB的长.
【分析】(1)根据对顶角和三角形内角和得到∠FBD=∠CAD,利用AAS定理证明;
(2)由全等可得DF=DC=2,BD=AD=1+2=3,再利用勾股定理可得答案.
【解答】(1)证明:∵AD⊥BC,BE⊥AC,
∴∠FDB=∠CDA=∠AEF=90°,
∵∠FBD+∠FDB+∠BFD=180°,
∠CAD+∠AEF+∠AFE=180°,
又∵∠BFD=∠AFE,
∴∠FBD=∠CAD,
∵在△ADC和△BDF中,
,
∴△ADC≌△BDF(AAS).
(2)解:由(1)得:DF=DC=2,
∴BD=AD=1+2=3,
Rt△ABD中,AB==3.
20.如图,BE⊥AE,CF⊥AE,垂足分别为E、F,D是EF的中点,CF=AF.
(1)请说明CD=BD;
(2)若BE=6,DE=3,请直接写出△ACD的面积.
【分析】(1)由BE⊥AE,CF⊥AE,得∠BED=∠CFD,再由D是EF的中点,得ED=FD,根据角边角公里可得出△BED与△CFD全等,进而可得结论;
(2)由全等可得CF=EB=6,然后可得DF=3,再计算出AD的长,利用三角形面积公式可得答案.
【解答】解:(1)∵BE⊥AE,CF⊥AE,
∴∠BED=∠CFD,
∵D是EF的中点,
∴ED=FD,
在△BED与△CFD中,
,
∴△BED≌△CFD(ASA),
∴CD=BD;
(2)由(1)得:CF=EB=6,
∵AF=CF,
∴AF=6,
∵D是EF的中点,
∴DF=DE=3,
∴AD=9,
∴△ACD的面积:AD CF=×9×6=27.
21.如图,点D、E、F、B在同一直线上,DE=BF,CE=AF,EC∥AF.
(1)求证:AB=CD;
(2)若∠A=30°,∠D=40°,求∠DEC的度数.
【分析】(1)根据平行线的性质和全等三角形的判定与性质可得结论;
(2)根据全等三角形的性质及三角形内角和定理可得答案.
【解答】(1)证明:∵EC∥AF,
∴∠CEB=∠AFD,
∴∠CED=∠AFB,
在△CED和△AFB中,
,
∴△CED≌△AFB(SAS),
∴AB=CD;
(2)解:由(1)得△CED≌△AFB,
∴∠C=∠A=40°,
∴∠DEC=180°﹣(∠D+∠C)=180°﹣(30°+40°)=110°.
22.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.
(1)求证:△ABD≌△EDC;
(2)若AB=2,BE=3,求CD的长.
【分析】(1)由“AAS”即可证△ABD≌△EDC;
(2)结合(1)可得AB=DE,BD=CD,可得结论.
【解答】(1)证明:∵AB∥CD,
∴∠ABD=∠EDC.
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
(2)∵△ABD≌△EDC,
∴AB=DE=2,BD=CD,
∴CD=BD=DE+BE=2+3=5.
23.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.
(1)求证:△ABE≌△CDF;
(2)连接BC,若∠CFD=100°,∠BCE=30°,求∠CBE的度数.
【分析】(1)根据SAS证明即可.
(2)利用全等三角形的性质以及三角形内角和定理解决问题即可.
【解答】(1)证明:∵AB∥CD,
∴∠A=∠DCF,
∵AF=CE,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS).
(2)∵△ABE≌△CDF,
∴∠AEB=∠CFD=100°,
∴∠BEC=180°﹣100°=80°,
∴∠CBE=180°﹣80°﹣30°=70°.
24.如图,在△ABC中,点D,E,F分别在AB,BC,AC上,∠B=∠C=∠DEF=60°,BD=CE.
(1)求证:∠BDE=∠CEF;
(2)若DE=3,求EF的长.
【分析】(1)由三角形内角和定理及平角的定义可得出答案;
(2)证明△BDE≌△CEF( ASA),由全等三角形的性质得出DE=EF.
【解答】(1)证明:∵∠B+∠BDE+∠BED=180°,∠DEF+∠FEC+∠BED=180°,∠B=∠DEF=60°,
∴∠BDE=∠CEF;
(2)解:在△BDE和△CEF中,
,
∴△BDE≌△CEF( ASA),
∴DE=EF,
∵DE=3,
∴EF=3.
25.如图,已知△ABC和△CDE均是直角三角形,∠ACB=∠CED=90°,AC=CE,AB⊥CD于点F.
(1)求证:△ABC≌△CDE;
(2)若点B是EC的中点,DE=10cm,求AE的长.
【分析】(1)根据ASA即可证明结论;
(2)结合(1)可得DE=BC=10cm,根据点B是EC的中点,可得EC=2BC=20cm,根据勾股定理即可求出AE的长.
【解答】(1)证明:∵AB⊥CD,
∴∠FAC+∠ACF=90°,
∵∠ACE=90°,
∴∠DCB+∠ACF=90°,
∴∠FAC=∠DCB,
∴AC=EC,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(ASA);
(2)解:∵△ABC≌△CDE,
∴DE=BC=10cm,
∵点B是EC的中点,
∴EC=2BC=20cm,
∴AC=EC=20cm,
在Rt△AEC中,根据勾股定理,得
AE==20(cm).
26.如图,AD⊥CD,BC⊥CD,∠AED=∠EBC,AD=CE,求证:AE=EB.
【分析】由“AAS”可证△ADE≌△ECB,可得AE=BE.
【解答】证明:∵AD⊥CD,BC⊥CD,
∴∠C=∠D=90°,
在△ADE和△ECB中,
,
∴△ADE≌△ECB(AAS),
∴AE=BE.
27.如图,△ABC中,AB=AC,AD是BC边上的高,CE是AB边上的高,AE=CE.
求证:(1)△AEF≌△CEB;
(2)AF=2CD.
【分析】(1)先证∠EAF=∠ECB,再结合∠AEF=∠CEB=90°且AE=CE利用全等三角形的判定得△AEF≌△CEB;
(2)由全等三角形的性质得AF=BC,由等腰三角形的性质“三线合一”得BC=2CD,等量代换得出结论.
【解答】证明:(1)∵CE⊥AB,
∴∠AEF=∠CEB=90°.
∴∠AFE+∠EAF=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CFD+∠ECB=90°,
又∵∠AFE=∠CFD,
∴∠EAF=∠ECB.
在△AEF和△CEB中,
,
∴△AEF≌△CEB(ASA);
(2)∵△AEF≌△CEB,
∴AF=BC,
∵AB=AC,AD⊥BC
∴CD=BD,BC=2CD.
∴AF=2CD.
28.如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,E是对角线AC上一点,连接BE,DE.
(1)求证:BE=DE.
(2)当BE∥CD,∠BAD=78°时,求∠BED的度数.
【分析】(1)由角平分线的性质得∠BAE=∠DAE,由SAS证得△BAE≌△DAE,即可得出结论;
(2)由△BAE≌△DAE,得出∠BEA=∠DEA,推出∠BEC=∠DEC,易求∠BAC=∠DAC=∠BAD=39°,由等腰三角形与三角形内角和定理求出∠ACD=∠ADC=70.5°,由平行线的定义得出∠BEC=∠ACD=70.5°,即可得出结果.
【解答】(1)证明:∵AC平分∠BAD,
∴∠BAE=∠DAE,
在△BAE和△DAE中,
,
∴△BAE≌△DAE(SAS),
∴BE=DE;
(2)解:由(1)得:△BAE≌△DAE,
∴∠BEA=∠DEA,
∴∠BEC=∠DEC,
∵AC平分∠BAD,∠BAD=78°,
∴∠BAC=∠DAC=∠BAD=×78°=39°,
∵AC=AD,
∴∠ACD=∠ADC=×(180°﹣39°)=70.5°,
∵BE∥CD,
∴∠BEC=∠ACD=70.5°,
∴∠BEC=∠DEC=70.5°,
∴∠BED=2×70.5°=141°.
29.如图,已知AB=AC,CD⊥AB,BE⊥AC,垂足分别为点D、E.求证:BD=CE.
【分析】由“AAS”可证△ABE≌△ACD,可得AD=AE,再根据线段的差可得BD=CE.
【解答】证明:∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°.
在△ABE和△ACD中
,
∴△ABE≌△ACD(AAS)
∴AD=AE,
又∵AB=AC,
∴BD=CE.
30.已知:如图,AB=DC,AC=DB,AC和BD相交于点O.点E是BC的中点,连接OE.
(1)求证:△ABC≌△DCB;
(2)求∠BEO的度数.
【分析】(1)根据“SSS”可以进行证明;
(2)由(1)得∠OBC=∠OCB,得到△BOC 是等腰三角形,再利用等腰三角形三线合一可得结论.
【解答】(1)证明:在△ABC和△DCB中,
,
∴△ABC≌△DCB(SSS).
(2)解:由(1)得:∠OBC=∠OCB,
∴△BOC 是等腰三角形.
∵点E是BC的中点,
∴OE⊥BC,
∴∠BEO=90°.
四.角平分线的性质(共11小题)
31.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.8 B.7.5 C.15 D.无法确定
【分析】过D点作DE⊥BC于E,如图,根据角平分线的性质得到DE=DA=3,然后根据三角形面积公式计算.
【解答】解:过D点作DE⊥BC于E,如图,
∵BD平分∠ABC,DE⊥BC,DA⊥AB,
∴DE=DA=3,
∴△BCD的面积=×5×3=7.5.
故选:B.
32.如图,已知△ABC中,∠C=90o,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,且AB=10,则△DEB的周长为( )
A.9 B.5 C.10 D.不能确定
【分析】先利用角平分线的性质得到DE=DC,再证明Rt△ACD≌Rt△AED得到AC=AE,然后利用等线段代换得到△DEB的周长=AB.
【解答】解:∵AD平分∠CAB,DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∵AC=BC,
∴BC=AE,
∴△DEB的周长=BD+DE+BE=BD+CD+BE=BC+BE=AE+BE=AB=10.
故选:C.
33.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D,DE=3cm,那么CE等于( )
A.cm B.2cm C.3cm D.4cm
【分析】直接利用角平分线的性质求解.
【解答】解:∵BE平分∠ABC,ED⊥AB,EC⊥BC,
∴EC=ED=3cm.
故选:C.
34.如图,三条公路两两相交,现计划修建一个油库,计划使得该油库到三条公路的距离相等,则油库的可选位置有( )处.
A.1 B.2 C.3 D.4
【分析】作三条公路所组成的三角形的内角平分线和外角平分线,然后根据角平分线的性质得到它们的交点满足条件.
【解答】解:如图,油库的可选位置有4处.
故选:D.
35.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,BC=10cm,点D到AB的距离为4cm,则DB=( )
A.6cm B.8cm C.5cm D.4cm
【分析】过点D作DE⊥AB于E,根据角平分线的性质得到DC=DE,结合图形计算,得到答案.
【解答】解:过点D作DE⊥AB于E,
由题意得,DE=4cm,
∵AD平分∠BAC,∠ACB=90°,DE⊥AB,
∴DC=DE=4(cm),
∴BD=BC﹣DC=6(cm),
故选:A.
36.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=9.6cm,则D到AB的距离为( )
A.2.2cm B.3.2cm C.4.8cm D.6.4cm
【分析】过D点作DE⊥AB于E,如图,先计算出DC=3.2cm,然后根据角平分线的性质得到DE=DC=3.2cm.
【解答】解:过D点作DE⊥AB于E,如图,
∵BD:DC=2:1,
∴DC=BC=×9.6=3.2(cm),
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DE=DC=3.2cm,
即D到AB的距离为3.2cm.
故选:B.
37.如图,AD是△ABC的角平分线,DF⊥AB于点F,且DE=DG,S△ADG=24,S△AED=18,则△DEF的面积为( )
A.2 B.3 C.4 D.6
【分析】过点D作DH⊥AC于H,根据角平分线的性质得到DH=DF,进而证明Rt△DEF≌Rt△DGH,根据全等三角形的性质得到△DEF的面积=△DGH的面积,根据题意列出方程,解方程得到答案.
【解答】解:过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DH=DF,
在Rt△DEF和Rt△DGH中,
,
∴Rt△DEF≌Rt△DGH(HL),
∴△DEF的面积=△DGH的面积,
设△DEF的面积=△DGH的面积=S,
同理可证,Rt△ADF≌Rt△ADH,
∴△ADF的面积=△ADH的面积,
∴24﹣S=18+S,
解得,S=3,
故选:B.
38.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=18,S△ABD=27,则CD的长为( )
A.4 B.8 C.3 D.6
【分析】过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得DE=CD,然后利用△ABD的面积公式列式计算即可得解.
【解答】解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=AB DE=×18 DE=27,
解得:DE=3,
∴CD=3.
故选:C.
39.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF⊥AB,交AB于点F,交BE于点D,若BC=8cm,DF=3cm,则△CDB的面积为( )
A.12cm2 B.8cm2 C.6cm2 D.4cm2
【分析】作DH⊥BC于点H,利用角平分线上的点到两边的距离相等,即可求出对应三角形的高,即可求解.
【解答】解:作DH⊥BC于点H,如图:
∵BE平分∠ABC,CF⊥AB,DH⊥BC.
∴DH=DF.
∵DF=3cm.
∴DH=3cm.
∵BC=8cm.
∴△CDB的面积为:=12cm2.
故选:A.
40.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是152cm2,AB=20cm,AC=18cm,求DE的长.
【分析】根据S△ABC=S△ABD+S△ACD,再利用角平分线的性质即可解决问题.
【解答】解:∵AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∵S△ABC=S△ABD+S△ACD,
∴S△ABC=,
∵△ABC面积是152cm2,AB=20cm,AC=18cm,
∴152=,
∴10DE+9DF=152,
∵DE=DF,
∴19DE=152,
∴DE=8.
41.如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长.
【分析】根据角平分线性质得出DE=DF,根据三角形的面积公式得出关于DE的方程,求出即可.
【解答】解:∵BD平分∠ABC交AC于点D,DE⊥AB,DF⊥BC,
∴DE=DF,
∵AB=6,BC=8,S△ABC=28,
∴S△ABC=S△ABD+S△BCD=AB DE+BC DF=DE (AB+BC)=28,
即DE(6+8)=28,∴DE=4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
全等三角形综合复习大全
知识梳理
三角形全等的判定一
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.
三角形全等的判定二
有两边和它们的夹角对应相等的两个三角形全等(简称“边角边”或“SAS”)
三角形全等的判定三
两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
三角形全等的判定四
两个角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”).
三角形全等的判定五
斜边与一直角边对应相等的两个直角三角形全等.(HL)
特别注意:全等三角形的判定中没有边边角定理,即不存在SSA定理
角平分线的性质定理:角平分线上的点到角两边的距离相等。
角平分线的判定定理:到一个角的两边的距离相等的点,在这个角的平分线上。
巩固练习
一.全等三角形的性质(共2小题)
1.如图,△ABC≌△DBE,∠ABC=80°,∠D=65°,则∠C的度数为( )
A.20° B.25° C.30° D.35°
2.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
二.全等三角形的判定(共6小题)
3.如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠A=∠D C.AC=DF D.AC∥FD
4.如图,在△ABC和△DCB中,∠ACB=∠DBC,添加一个条件,不能证明△ABC和△DCB全等的是( )
A.∠ABC=∠DCB B.AB=DC C.AC=DB D.∠A=∠D
5.如图,已知AD=AE,∠B=∠C.求证:△ACD≌△ABE.
6.如图,点A、F、C、D在同一各直线上.AB∥DE.AB=DE,AF=DC.求证:△ABC≌△DEF.
7.如图,在△ABC和△DEF中,边AC,DE交于点H,AB∥DE,AB=DE,BE=CF.
(1)若∠B=55°,∠ACB=100°,求∠CHE的度数.
(2)求证:△ABC≌△DEF.
8.已知:如图,AB∥CD,AB=CD,BE=CF.
求证:△ABF≌△DCE.
三.全等三角形的判定与性质(共22小题)
9.如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,若∠A=40°,则∠FDE= .
10.如图,AD是△ABC的中线,E是AC上的一点,BE交AD于F,已知AC=BF,∠DAC=25°,∠EBC=30°,∠C= .
11.如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连接AD、CD.若∠B=65°,则∠ADC的大小为 度.
12.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:AD+DE=BC;
(2)若∠BDC=70°,求∠ADB的度数.
13.如图,在△ABC中,AB=AC,D是边BC延长线上一点,连接AD,过A做AE=AD,且∠DAE=∠BAC,连接CE交AD于点F.
(1)求证:△ABD≌△ACE;
(2)若∠FCD=34°,求∠B的度数.
14.如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于E点,DE=EF.
(1)求证:△ADE≌△CFE;
(2)若AB=5,CF=4,求BD的长.
15.如图,在△ABC中,D是边BC上的点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF,CE=BF.求证:∠B=∠C.
16.如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)求∠EAF的度数.
17.如图,在四边形ABCD中,AB∥CD,连接BD,点E在BD上,连接CE,若∠1=∠2,AB=ED,求证:DB=CD.
18.如图,AC∥BD,∠C=90°,AC=BE,AB=DE,求证:DE⊥AB.
19.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,BE,AD相交于点F,BF=AC.
(1)求证:△BDF≌△ADC.
(2)若AF=1,DC=2,求AB的长.
20.如图,BE⊥AE,CF⊥AE,垂足分别为E、F,D是EF的中点,CF=AF.
(1)请说明CD=BD;
(2)若BE=6,DE=3,请直接写出△ACD的面积.
21.如图,点D、E、F、B在同一直线上,DE=BF,CE=AF,EC∥AF.
(1)求证:AB=CD;
(2)若∠A=30°,∠D=40°,求∠DEC的度数.
22.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.
(1)求证:△ABD≌△EDC;
(2)若AB=2,BE=3,求CD的长.
23.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.
(1)求证:△ABE≌△CDF;
(2)连接BC,若∠CFD=100°,∠BCE=30°,求∠CBE的度数.
24.如图,在△ABC中,点D,E,F分别在AB,BC,AC上,∠B=∠C=∠DEF=60°,BD=CE.
(1)求证:∠BDE=∠CEF;
(2)若DE=3,求EF的长.
25.如图,已知△ABC和△CDE均是直角三角形,∠ACB=∠CED=90°,AC=CE,AB⊥CD于点F.
(1)求证:△ABC≌△CDE;
(2)若点B是EC的中点,DE=10cm,求AE的长.
26.如图,AD⊥CD,BC⊥CD,∠AED=∠EBC,AD=CE,求证:AE=EB.
27.如图,△ABC中,AB=AC,AD是BC边上的高,CE是AB边上的高,AE=CE.
求证:(1)△AEF≌△CEB;
(2)AF=2CD.
28.如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,E是对角线AC上一点,连接BE,DE.
(1)求证:BE=DE.
(2)当BE∥CD,∠BAD=78°时,求∠BED的度数.
29.如图,已知AB=AC,CD⊥AB,BE⊥AC,垂足分别为点D、E.求证:BD=CE.
30.已知:如图,AB=DC,AC=DB,AC和BD相交于点O.点E是BC的中点,连接OE.
(1)求证:△ABC≌△DCB;
(2)求∠BEO的度数.
四.角平分线的性质(共11小题)
31.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.8 B.7.5 C.15 D.无法确定
32.如图,已知△ABC中,∠C=90o,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,且AB=10,则△DEB的周长为( )
A.9 B.5 C.10 D.不能确定
33.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D,DE=3cm,那么CE等于( )
A.cm B.2cm C.3cm D.4cm
34.如图,三条公路两两相交,现计划修建一个油库,计划使得该油库到三条公路的距离相等,则油库的可选位置有( )处.
A.1 B.2 C.3 D.4
35.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,BC=10cm,点D到AB的距离为4cm,则DB=( )
A.6cm B.8cm C.5cm D.4cm
36.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=9.6cm,则D到AB的距离为( )
A.2.2cm B.3.2cm C.4.8cm D.6.4cm
37.如图,AD是△ABC的角平分线,DF⊥AB于点F,且DE=DG,S△ADG=24,S△AED=18,则△DEF的面积为( )
A.2 B.3 C.4 D.6
38.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=18,S△ABD=27,则CD的长为( )
A.4 B.8 C.3 D.6
39.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF⊥AB,交AB于点F,交BE于点D,若BC=8cm,DF=3cm,则△CDB的面积为( )
A.12cm2 B.8cm2 C.6cm2 D.4cm2
40.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是152cm2,AB=20cm,AC=18cm,求DE的长.
41.如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长.
全等三角形
参考答案与试题解析
一.全等三角形的性质(共2小题)
1.如图,△ABC≌△DBE,∠ABC=80°,∠D=65°,则∠C的度数为( )
A.20° B.25° C.30° D.35°
【分析】根据全等三角形的对应角相等得到∠DBE=∠ABC,根据三角形内角和定理计算,得到答案.
【解答】解:∵△ABC≌△DBE,∠ABC=80°,
∴∠DBE=∠ABC=80°,
∵∠D=65°,
∴∠C=180°﹣∠DBE﹣∠D=35°,
故选:D.
2.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
【分析】(1)根据全等三角形的性质得到AB=DE=10,BE=BC=4,结合图形计算,得到答案;
(2)根据全等三角形的性质得到∠BAC=∠D=30°,∠DBE=∠C=70°,根据三角形内角和定理求出∠ABC,计算即可.
【解答】解:(1)∵△ABC≌△DEB,DE=10,BC=4,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠C=70°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
二.全等三角形的判定(共6小题)
3.如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠A=∠D C.AC=DF D.AC∥FD
【分析】根据全等三角形的判定方法,可以判断添加各个选项中的条件是否能够判断△ABC≌△DEF,本题得以解决.
【解答】解:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
又∵∠B=∠E,
∴当添加条件AB=DE时,△ABC≌△DEF(SAS),故选项A不符合题意;
当添加条件∠A=∠D时,△ABC≌△DEF(AAS),故选项B不符合题意;
当添加条件AC=DF时,无法判断△ABC≌△DEF,故选项C符合题意;
当添加条件AC∥FD时,则∠ACB=∠DFE,故△ABC≌△DEF(ASA),故选项D不符合题意;
故选:C.
4.如图,在△ABC和△DCB中,∠ACB=∠DBC,添加一个条件,不能证明△ABC和△DCB全等的是( )
A.∠ABC=∠DCB B.AB=DC C.AC=DB D.∠A=∠D
【分析】根据证明三角形全等的条件AAS,SAS,ASA,SSS逐一验证选项即可.
【解答】解:在△ABC和△DCB中,
∵∠ACB=∠DBC,BC=BC,
A:当∠ABC=∠DCB时,△ABC≌△DCB(ASA),
故A能证明;
B:当AB=DC时,不能证明两三角形全等,
故B不能证明;
C:当AC=DB时,△ABC≌△DCB(SAS),
故C能证明;
D:当∠A=∠D时,△ABC≌△DCB(AAS),
故D能证明;
故选:B.
5.如图,已知AD=AE,∠B=∠C.求证:△ACD≌△ABE.
【分析】根据题目中的条件,利用AAS可以证明△ACD≌△ABE.
【解答】证明:在△ACD和△ABE中,
,
∴△ACD≌△ABE(AAS).
6.如图,点A、F、C、D在同一各直线上.AB∥DE.AB=DE,AF=DC.求证:△ABC≌△DEF.
【分析】根据平行线的性质得出∠A=∠D,求出AC=DF,再根据全等三角形的判定定理推出即可.
【解答】证明:∵AB∥DE,
∴∠A=∠D,
∵AF=DC,
∴AF+CF=DC+CF,
即AC=DF,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
7.如图,在△ABC和△DEF中,边AC,DE交于点H,AB∥DE,AB=DE,BE=CF.
(1)若∠B=55°,∠ACB=100°,求∠CHE的度数.
(2)求证:△ABC≌△DEF.
【分析】(1)根据三角形内角和定理求出∠A,再根据平行线的性质得出∠CHE=∠A即可;
(2)根据平行线的性质得出∠B=∠DEF,求出BC=EF,再根据全等三角形的判定定理推出即可.
【解答】(1)解:∵∠B=55°,∠ACB=100°,
∴∠A=180°﹣∠B﹣∠ACB=25°,
∵AB∥DE,
∴∠CHE=∠A=25°;
(2)证明:∵AB∥DE,
∴∠B=∠DEF,
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
8.已知:如图,AB∥CD,AB=CD,BE=CF.
求证:△ABF≌△DCE.
【分析】根据BE=CF求出BF=CE,根据平行线的性质得出∠B=∠C,再根据全等三角形的判定定理推出即可.
【解答】证明:∵BE=CF,
∴BE﹣EF=CF﹣EF,
即BF=CE,
∵AB∥CD,
∴∠B=∠C,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(SAS).
三.全等三角形的判定与性质(共22小题)
9.如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,若∠A=40°,则∠FDE= 70° .
【分析】根据全等三角形的判定推出△BFD≌△CDE,根据全等三角形的性质得出∠BFD=∠CDE,根据三角形的内角和定理求出∠B=∠C=(180°﹣∠A)=70°,求出∠FDB+∠EDC=∠FDB+∠BFD=180°﹣∠B=110°,再求出答案即可.
【解答】解:在△BFD和△CDE中,
,
∴△BFD≌△CDE(SAS),
∴∠BFD=∠CDE,
∵∠B=∠C,∠A=40°,
∴∠B=∠C=(180°﹣∠A)=70°,
∴∠FDB+∠CDE=∠FDB+∠BFD=180°﹣∠B=110°,
∴∠FDE=180°﹣(∠FDB+∠EDC)=180°﹣110°=70°,
故答案为:70°.
10.如图,AD是△ABC的中线,E是AC上的一点,BE交AD于F,已知AC=BF,∠DAC=25°,∠EBC=30°,∠C= 100° .
【分析】延长AD到M,使得DM=AD,连接BM,证△BDM≌△CDA(SAS),得BM=AC=BF,∠M=∠DAC=25°,∠C=∠DBM,再证△BFM是等腰三角形,求出∠MBF的度数,即可解决问题.
【解答】解:如图,延长AD到M,使得DM=AD,连接BM,如图所示:
在△BDM和△CDA中,
,
∴△BDM≌△CDA(SAS),
∴BM=AC=BF,∠M=∠DAC=25°,∠C=∠DBM,
∵BF=AC,
∴BF=BM,
∴∠M=∠BFM=25°,
∴∠MBF=180°﹣∠M﹣∠BFM=130°,
∵∠EBC=30°,
∴∠DBM=∠MBF﹣∠EBC=100°,
∴∠C=∠DBM=100°,
故答案为:100°.
11.如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连接AD、CD.若∠B=65°,则∠ADC的大小为 65 度.
【分析】根据作法可得AB=CD,BC=AD,然后利用“边边边”证明△ABC和△CDA全等,再根据全等三角形对应角相等解答.
【解答】解:∵以点A为圆心,以BC长为半径作弧;以顶点C为圆心,以AB长为半径作弧,两弧交于点D,
∴AB=CD,BC=AD,
在△ABC和△CDA中,
,
∴△ABC≌△CDA(SSS),
∴∠ADC=∠B=65°.
故答案为:65.
12.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:AD+DE=BC;
(2)若∠BDC=70°,求∠ADB的度数.
【分析】(1)由“ASA”可证△ADB≌△EBC,可得BC=BD,可得结论;
(2)由等腰三角形的性质可得∠BDC=∠BCD=70°,即可求解.
【解答】证明:(1)∵AD∥BC,
∴∠ADB=∠CBE,
在△ADB和△EBC中,
,
∴△ADB≌△EBC(ASA),
∴BC=BD,
∵BE+DE=DB,
∴AD+DE=BC;
(2)∵BC=BD,
∴∠BDC=∠BCD=70°,
∴∠DBC=40°,
∴∠ADB=40°.
13.如图,在△ABC中,AB=AC,D是边BC延长线上一点,连接AD,过A做AE=AD,且∠DAE=∠BAC,连接CE交AD于点F.
(1)求证:△ABD≌△ACE;
(2)若∠FCD=34°,求∠B的度数.
【分析】(1)根据题意AB=AC、AE=AD,只需证明其对应两边的夹角相等即可证明△ABD≌△ACE;
(2)根据图形得出∠ACB+ACE+∠FCE=180°,将相等的角代入求解即可.
【解答】(1)证明:∵∠DAE=∠BAC,
∴∠DAE+∠DAC=∠BAC+∠DAC,即∠EAC=∠DAB,
在△ABD和△ACE中,
,
∴△ABD∽△ACE(SAS).
(2)由(1)可知∠B=∠ACB=ACE,
∵∠ACB+ACE+∠FCE=180°,
即2∠B+34°=180°,
∴∠B=73°.
14.如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于E点,DE=EF.
(1)求证:△ADE≌△CFE;
(2)若AB=5,CF=4,求BD的长.
【分析】(1)利用角角边定理判定即可;
(2)利用全等三角形对应边相等可得AD的长,用AB﹣AD即可得出结论.
【解答】(1)证明:∵CF∥AB,
∴∠ADF=∠F,∠A=∠ECF.
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS).
(2)∵△ADE≌△CFE,
∴AD=CF=4.
∴BD=AB﹣AD=5﹣4=1.
15.如图,在△ABC中,D是边BC上的点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF,CE=BF.求证:∠B=∠C.
【分析】由垂直的定义,DE=DF,CE=BF证明△BDF≌△CDE,得出对应角相等即可.
【解答】证明:∵DE⊥AC,DF⊥AB,
∴∠BFD=∠CED=90°,
在△BDF和△CDE中,
,
∴△BDF≌△CDE(SAS),
∴∠B=∠C.
16.如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)求∠EAF的度数.
【分析】(1)利用SAS证明△AEB≌△FAC可证明结论;
(2)由全等三角形的性质可得∠E=∠CAF,由余角的定义可求得∠EAF的度数.
【解答】(1)证明:∵CD⊥AB,BE⊥AC,
∴∠CAD+∠ACD=∠CAD+∠EBA=90°,
∴∠ACD=∠EBA,
在△AEB和△FAC中,
,
∴△AEB≌△FAC(SAS),
∴AE=FA;
(2)解:∵△AEB≌△FAC,
∴∠E=∠CAF,
∵∠E+∠EAG=90°,
∴∠CAF+∠EAG=90°,
即∠EAF=90°.
17.如图,在四边形ABCD中,AB∥CD,连接BD,点E在BD上,连接CE,若∠1=∠2,AB=ED,求证:DB=CD.
【分析】根据AB∥CD,可得∠ABD=∠EDC,利用AAS证明△ABD≌△EDC,即可得结论.
【解答】证明:∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
∴DB=CD.
18.如图,AC∥BD,∠C=90°,AC=BE,AB=DE,求证:DE⊥AB.
【分析】先根据平行线的性质求出∠DBE=∠C=90°,再由HL定理可判定△ACB≌△EBD,由全等三角形的性质解答即可.
【解答】证明:设AB与DE相交于点M,
∵AC∥BD,
∴∠C+∠DBE=180°,
∵∠C=90°,
∴∠DBE=90°,
在Rt△ACB与Rt△EBD中,
,
∴Rt△ACB≌Rt△EBD(HL),
∴∠ABC=∠D,
∵∠D+∠MEB=90°,
∴∠ABC+∠MEB=90°,
∴∠EMB=180°﹣∠ABC﹣∠MEB=90°,
∴DE⊥AB.
19.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,BE,AD相交于点F,BF=AC.
(1)求证:△BDF≌△ADC.
(2)若AF=1,DC=2,求AB的长.
【分析】(1)根据对顶角和三角形内角和得到∠FBD=∠CAD,利用AAS定理证明;
(2)由全等可得DF=DC=2,BD=AD=1+2=3,再利用勾股定理可得答案.
【解答】(1)证明:∵AD⊥BC,BE⊥AC,
∴∠FDB=∠CDA=∠AEF=90°,
∵∠FBD+∠FDB+∠BFD=180°,
∠CAD+∠AEF+∠AFE=180°,
又∵∠BFD=∠AFE,
∴∠FBD=∠CAD,
∵在△ADC和△BDF中,
,
∴△ADC≌△BDF(AAS).
(2)解:由(1)得:DF=DC=2,
∴BD=AD=1+2=3,
Rt△ABD中,AB==3.
20.如图,BE⊥AE,CF⊥AE,垂足分别为E、F,D是EF的中点,CF=AF.
(1)请说明CD=BD;
(2)若BE=6,DE=3,请直接写出△ACD的面积.
【分析】(1)由BE⊥AE,CF⊥AE,得∠BED=∠CFD,再由D是EF的中点,得ED=FD,根据角边角公里可得出△BED与△CFD全等,进而可得结论;
(2)由全等可得CF=EB=6,然后可得DF=3,再计算出AD的长,利用三角形面积公式可得答案.
【解答】解:(1)∵BE⊥AE,CF⊥AE,
∴∠BED=∠CFD,
∵D是EF的中点,
∴ED=FD,
在△BED与△CFD中,
,
∴△BED≌△CFD(ASA),
∴CD=BD;
(2)由(1)得:CF=EB=6,
∵AF=CF,
∴AF=6,
∵D是EF的中点,
∴DF=DE=3,
∴AD=9,
∴△ACD的面积:AD CF=×9×6=27.
21.如图,点D、E、F、B在同一直线上,DE=BF,CE=AF,EC∥AF.
(1)求证:AB=CD;
(2)若∠A=30°,∠D=40°,求∠DEC的度数.
【分析】(1)根据平行线的性质和全等三角形的判定与性质可得结论;
(2)根据全等三角形的性质及三角形内角和定理可得答案.
【解答】(1)证明:∵EC∥AF,
∴∠CEB=∠AFD,
∴∠CED=∠AFB,
在△CED和△AFB中,
,
∴△CED≌△AFB(SAS),
∴AB=CD;
(2)解:由(1)得△CED≌△AFB,
∴∠C=∠A=40°,
∴∠DEC=180°﹣(∠D+∠C)=180°﹣(30°+40°)=110°.
22.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.
(1)求证:△ABD≌△EDC;
(2)若AB=2,BE=3,求CD的长.
【分析】(1)由“AAS”即可证△ABD≌△EDC;
(2)结合(1)可得AB=DE,BD=CD,可得结论.
【解答】(1)证明:∵AB∥CD,
∴∠ABD=∠EDC.
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
(2)∵△ABD≌△EDC,
∴AB=DE=2,BD=CD,
∴CD=BD=DE+BE=2+3=5.
23.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.
(1)求证:△ABE≌△CDF;
(2)连接BC,若∠CFD=100°,∠BCE=30°,求∠CBE的度数.
【分析】(1)根据SAS证明即可.
(2)利用全等三角形的性质以及三角形内角和定理解决问题即可.
【解答】(1)证明:∵AB∥CD,
∴∠A=∠DCF,
∵AF=CE,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS).
(2)∵△ABE≌△CDF,
∴∠AEB=∠CFD=100°,
∴∠BEC=180°﹣100°=80°,
∴∠CBE=180°﹣80°﹣30°=70°.
24.如图,在△ABC中,点D,E,F分别在AB,BC,AC上,∠B=∠C=∠DEF=60°,BD=CE.
(1)求证:∠BDE=∠CEF;
(2)若DE=3,求EF的长.
【分析】(1)由三角形内角和定理及平角的定义可得出答案;
(2)证明△BDE≌△CEF( ASA),由全等三角形的性质得出DE=EF.
【解答】(1)证明:∵∠B+∠BDE+∠BED=180°,∠DEF+∠FEC+∠BED=180°,∠B=∠DEF=60°,
∴∠BDE=∠CEF;
(2)解:在△BDE和△CEF中,
,
∴△BDE≌△CEF( ASA),
∴DE=EF,
∵DE=3,
∴EF=3.
25.如图,已知△ABC和△CDE均是直角三角形,∠ACB=∠CED=90°,AC=CE,AB⊥CD于点F.
(1)求证:△ABC≌△CDE;
(2)若点B是EC的中点,DE=10cm,求AE的长.
【分析】(1)根据ASA即可证明结论;
(2)结合(1)可得DE=BC=10cm,根据点B是EC的中点,可得EC=2BC=20cm,根据勾股定理即可求出AE的长.
【解答】(1)证明:∵AB⊥CD,
∴∠FAC+∠ACF=90°,
∵∠ACE=90°,
∴∠DCB+∠ACF=90°,
∴∠FAC=∠DCB,
∴AC=EC,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(ASA);
(2)解:∵△ABC≌△CDE,
∴DE=BC=10cm,
∵点B是EC的中点,
∴EC=2BC=20cm,
∴AC=EC=20cm,
在Rt△AEC中,根据勾股定理,得
AE==20(cm).
26.如图,AD⊥CD,BC⊥CD,∠AED=∠EBC,AD=CE,求证:AE=EB.
【分析】由“AAS”可证△ADE≌△ECB,可得AE=BE.
【解答】证明:∵AD⊥CD,BC⊥CD,
∴∠C=∠D=90°,
在△ADE和△ECB中,
,
∴△ADE≌△ECB(AAS),
∴AE=BE.
27.如图,△ABC中,AB=AC,AD是BC边上的高,CE是AB边上的高,AE=CE.
求证:(1)△AEF≌△CEB;
(2)AF=2CD.
【分析】(1)先证∠EAF=∠ECB,再结合∠AEF=∠CEB=90°且AE=CE利用全等三角形的判定得△AEF≌△CEB;
(2)由全等三角形的性质得AF=BC,由等腰三角形的性质“三线合一”得BC=2CD,等量代换得出结论.
【解答】证明:(1)∵CE⊥AB,
∴∠AEF=∠CEB=90°.
∴∠AFE+∠EAF=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CFD+∠ECB=90°,
又∵∠AFE=∠CFD,
∴∠EAF=∠ECB.
在△AEF和△CEB中,
,
∴△AEF≌△CEB(ASA);
(2)∵△AEF≌△CEB,
∴AF=BC,
∵AB=AC,AD⊥BC
∴CD=BD,BC=2CD.
∴AF=2CD.
28.如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,E是对角线AC上一点,连接BE,DE.
(1)求证:BE=DE.
(2)当BE∥CD,∠BAD=78°时,求∠BED的度数.
【分析】(1)由角平分线的性质得∠BAE=∠DAE,由SAS证得△BAE≌△DAE,即可得出结论;
(2)由△BAE≌△DAE,得出∠BEA=∠DEA,推出∠BEC=∠DEC,易求∠BAC=∠DAC=∠BAD=39°,由等腰三角形与三角形内角和定理求出∠ACD=∠ADC=70.5°,由平行线的定义得出∠BEC=∠ACD=70.5°,即可得出结果.
【解答】(1)证明:∵AC平分∠BAD,
∴∠BAE=∠DAE,
在△BAE和△DAE中,
,
∴△BAE≌△DAE(SAS),
∴BE=DE;
(2)解:由(1)得:△BAE≌△DAE,
∴∠BEA=∠DEA,
∴∠BEC=∠DEC,
∵AC平分∠BAD,∠BAD=78°,
∴∠BAC=∠DAC=∠BAD=×78°=39°,
∵AC=AD,
∴∠ACD=∠ADC=×(180°﹣39°)=70.5°,
∵BE∥CD,
∴∠BEC=∠ACD=70.5°,
∴∠BEC=∠DEC=70.5°,
∴∠BED=2×70.5°=141°.
29.如图,已知AB=AC,CD⊥AB,BE⊥AC,垂足分别为点D、E.求证:BD=CE.
【分析】由“AAS”可证△ABE≌△ACD,可得AD=AE,再根据线段的差可得BD=CE.
【解答】证明:∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°.
在△ABE和△ACD中
,
∴△ABE≌△ACD(AAS)
∴AD=AE,
又∵AB=AC,
∴BD=CE.
30.已知:如图,AB=DC,AC=DB,AC和BD相交于点O.点E是BC的中点,连接OE.
(1)求证:△ABC≌△DCB;
(2)求∠BEO的度数.
【分析】(1)根据“SSS”可以进行证明;
(2)由(1)得∠OBC=∠OCB,得到△BOC 是等腰三角形,再利用等腰三角形三线合一可得结论.
【解答】(1)证明:在△ABC和△DCB中,
,
∴△ABC≌△DCB(SSS).
(2)解:由(1)得:∠OBC=∠OCB,
∴△BOC 是等腰三角形.
∵点E是BC的中点,
∴OE⊥BC,
∴∠BEO=90°.
四.角平分线的性质(共11小题)
31.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.8 B.7.5 C.15 D.无法确定
【分析】过D点作DE⊥BC于E,如图,根据角平分线的性质得到DE=DA=3,然后根据三角形面积公式计算.
【解答】解:过D点作DE⊥BC于E,如图,
∵BD平分∠ABC,DE⊥BC,DA⊥AB,
∴DE=DA=3,
∴△BCD的面积=×5×3=7.5.
故选:B.
32.如图,已知△ABC中,∠C=90o,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,且AB=10,则△DEB的周长为( )
A.9 B.5 C.10 D.不能确定
【分析】先利用角平分线的性质得到DE=DC,再证明Rt△ACD≌Rt△AED得到AC=AE,然后利用等线段代换得到△DEB的周长=AB.
【解答】解:∵AD平分∠CAB,DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∵AC=BC,
∴BC=AE,
∴△DEB的周长=BD+DE+BE=BD+CD+BE=BC+BE=AE+BE=AB=10.
故选:C.
33.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D,DE=3cm,那么CE等于( )
A.cm B.2cm C.3cm D.4cm
【分析】直接利用角平分线的性质求解.
【解答】解:∵BE平分∠ABC,ED⊥AB,EC⊥BC,
∴EC=ED=3cm.
故选:C.
34.如图,三条公路两两相交,现计划修建一个油库,计划使得该油库到三条公路的距离相等,则油库的可选位置有( )处.
A.1 B.2 C.3 D.4
【分析】作三条公路所组成的三角形的内角平分线和外角平分线,然后根据角平分线的性质得到它们的交点满足条件.
【解答】解:如图,油库的可选位置有4处.
故选:D.
35.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,BC=10cm,点D到AB的距离为4cm,则DB=( )
A.6cm B.8cm C.5cm D.4cm
【分析】过点D作DE⊥AB于E,根据角平分线的性质得到DC=DE,结合图形计算,得到答案.
【解答】解:过点D作DE⊥AB于E,
由题意得,DE=4cm,
∵AD平分∠BAC,∠ACB=90°,DE⊥AB,
∴DC=DE=4(cm),
∴BD=BC﹣DC=6(cm),
故选:A.
36.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=9.6cm,则D到AB的距离为( )
A.2.2cm B.3.2cm C.4.8cm D.6.4cm
【分析】过D点作DE⊥AB于E,如图,先计算出DC=3.2cm,然后根据角平分线的性质得到DE=DC=3.2cm.
【解答】解:过D点作DE⊥AB于E,如图,
∵BD:DC=2:1,
∴DC=BC=×9.6=3.2(cm),
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DE=DC=3.2cm,
即D到AB的距离为3.2cm.
故选:B.
37.如图,AD是△ABC的角平分线,DF⊥AB于点F,且DE=DG,S△ADG=24,S△AED=18,则△DEF的面积为( )
A.2 B.3 C.4 D.6
【分析】过点D作DH⊥AC于H,根据角平分线的性质得到DH=DF,进而证明Rt△DEF≌Rt△DGH,根据全等三角形的性质得到△DEF的面积=△DGH的面积,根据题意列出方程,解方程得到答案.
【解答】解:过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DH=DF,
在Rt△DEF和Rt△DGH中,
,
∴Rt△DEF≌Rt△DGH(HL),
∴△DEF的面积=△DGH的面积,
设△DEF的面积=△DGH的面积=S,
同理可证,Rt△ADF≌Rt△ADH,
∴△ADF的面积=△ADH的面积,
∴24﹣S=18+S,
解得,S=3,
故选:B.
38.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=18,S△ABD=27,则CD的长为( )
A.4 B.8 C.3 D.6
【分析】过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得DE=CD,然后利用△ABD的面积公式列式计算即可得解.
【解答】解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=AB DE=×18 DE=27,
解得:DE=3,
∴CD=3.
故选:C.
39.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF⊥AB,交AB于点F,交BE于点D,若BC=8cm,DF=3cm,则△CDB的面积为( )
A.12cm2 B.8cm2 C.6cm2 D.4cm2
【分析】作DH⊥BC于点H,利用角平分线上的点到两边的距离相等,即可求出对应三角形的高,即可求解.
【解答】解:作DH⊥BC于点H,如图:
∵BE平分∠ABC,CF⊥AB,DH⊥BC.
∴DH=DF.
∵DF=3cm.
∴DH=3cm.
∵BC=8cm.
∴△CDB的面积为:=12cm2.
故选:A.
40.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是152cm2,AB=20cm,AC=18cm,求DE的长.
【分析】根据S△ABC=S△ABD+S△ACD,再利用角平分线的性质即可解决问题.
【解答】解:∵AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∵S△ABC=S△ABD+S△ACD,
∴S△ABC=,
∵△ABC面积是152cm2,AB=20cm,AC=18cm,
∴152=,
∴10DE+9DF=152,
∵DE=DF,
∴19DE=152,
∴DE=8.
41.如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长.
【分析】根据角平分线性质得出DE=DF,根据三角形的面积公式得出关于DE的方程,求出即可.
【解答】解:∵BD平分∠ABC交AC于点D,DE⊥AB,DF⊥BC,
∴DE=DF,
∵AB=6,BC=8,S△ABC=28,
∴S△ABC=S△ABD+S△BCD=AB DE+BC DF=DE (AB+BC)=28,
即DE(6+8)=28,∴DE=4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
