2021-2022学年华东师大版数学七年级上册3.3.3升幂排列与降幂排列课件(第三课时 20张)
文档属性
| 名称 | 2021-2022学年华东师大版数学七年级上册3.3.3升幂排列与降幂排列课件(第三课时 20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 692.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 11:09:13 | ||
图片预览







文档简介
(共20张PPT)
3.升幂排列和降幂排列
华东师大版七年级(上册)
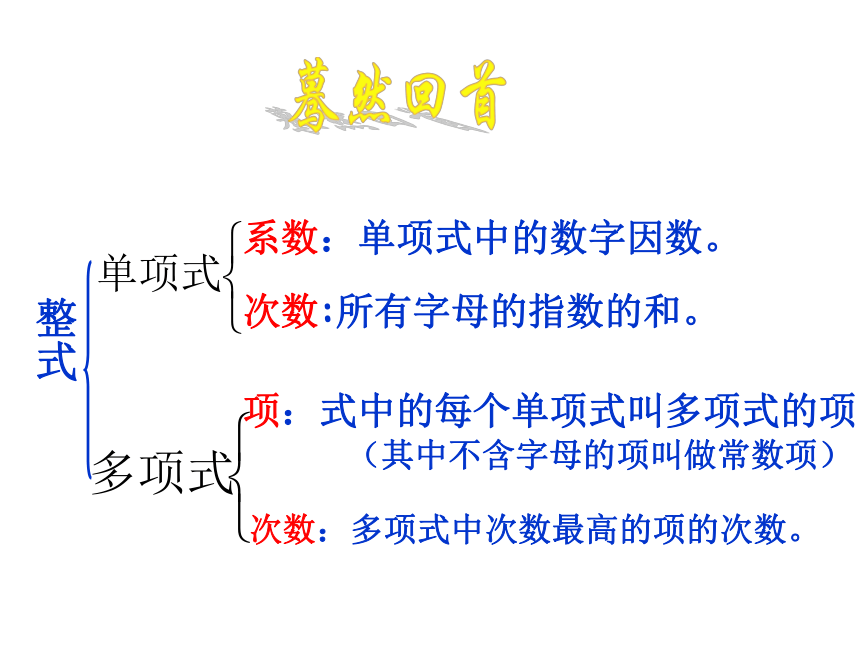
次数:所有字母的指数的和。
系数:单项式中的数字因数。
项:式中的每个单项式叫多项式的项。
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数。
整式
成长的足迹
1. 单项式m2n2的系数是_______,
次数是______, m2n2是____次单项式.
2. 多项式x+y-z是单项式 , ,___的和,它是___次___项式.
3. 多项式3m3-2m-5+m2的常数项是____,
一次项是_____, 二次项的系数是_____.
1
4
4
x
y
-z
1
3
-2m
-2
4.如果-5xym-1为4次单项式,则m=____.
4
5.若-ax2yb+1是关于x、y的五次单项式,且系数为-1/2,则a= ,b= .
1/2
2
6.下列说法中,正确的是( )
D
成长的足迹
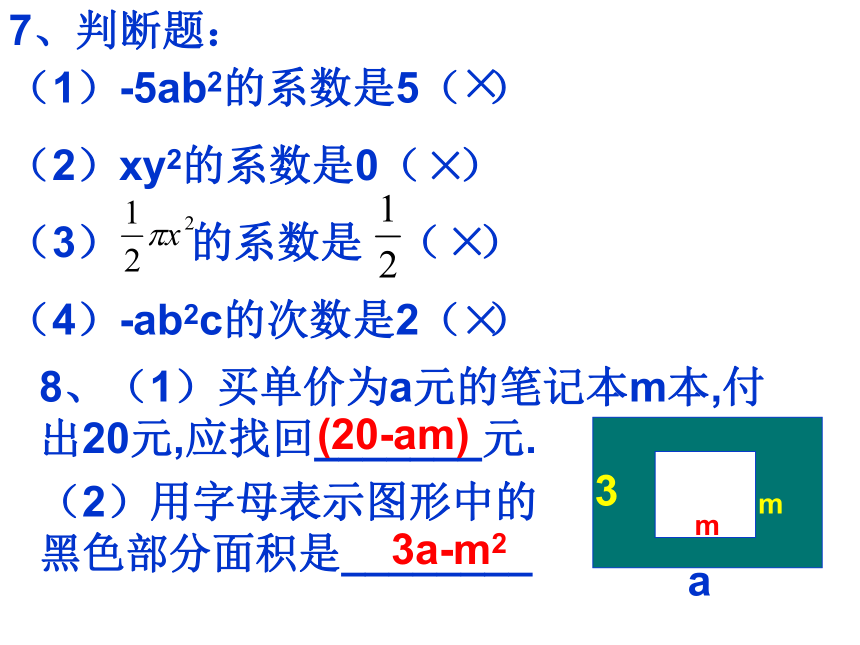
8、(1)买单价为a元的笔记本m本,付出20元,应找回_______元.
(20-am)
(2)用字母表示图形中的黑色部分面积是________
a
3
m
m
3a-m2
7、判断题:
(1)-5ab2的系数是5( )
(2)xy2的系数是0( )
(3) 的系数是 ( )
(4)-ab2c的次数是2( )
×
×
×
×
9.下列式子中哪些是单项式,哪些是多项式,哪些是整式
10.己知多项式
不含x3项和x2项,求当x=-1时这个多项式的值.
解:根据题意,有
{
{
∴
∴
原多项式为
当x=-1时,
11.已知代数式3xn-(m-1)x+1是关于x的三次二项式,求m、n的值。
12. 是 次 项式,其中三次项系数是 ,二次项为 ,常数项为 ,写出所有的项 。
三
三
多项式x +x+1的项是_____
问题1.如果交换多项式各项位置,所得到
的多项式与原多项式是否相等?为什么?
相等(加法交换律)
问题2.任意交换x +x+1中各项的位置,可以得到几种不同的排列方式?请一一列举出来.
可以得到6种不同的排列方式,即x +x+1, x+x +1, x+1+x , x +1+x, 1+x+ x , 1+x +x.
问题3.以上六种排列中,你认为哪几种比较整齐?
x +x+1 ,1+x+ x 这样的排列比较整齐.
问题4.你认为是什么特点使得两种排列比较整齐呢?
这两种排列有一个共同特点,那就是x的指数是逐渐变小(或变大)的.
这样整齐的写法除了美观之外,还会为今后的计算带来方便。因而我们常常把一个多项式各项的位置按照其中某一个字母的指数大小顺序来排列.
例如把多项式 按x的指数从大到小的顺序排列是 ,按x指数从小到大的顺序排列是 .
降幂排列:把一个多项式按某个字母的指数按从大到小的顺序排列起来,叫做把多项式按这个字母降幂排列。
升幂排列:把一个多项式按某个字母的指数按从小到大的顺序排列起来,叫做把多项式按这个字母升幂排列。
如 是按x的降幂排列
如 是按x的升幂排列
提问:
1. x +x+1是按x的____排列.
2. 1+x+x 是按x的____排列.
降幂
升幂
例1、把多项式
按r升幂进行排列。
解:按r升幂进行排列是:
注意
交换位置时,符号跟项走,第一项系数为正数时,正号可以省略.
例2:把多项式 重新排列.
注意:
含有两个或两个以上字母的多项式,常常按照其中某一字母升幂或降幂排列.
(1) 按a升幂排列 ; (2)按a降幂排列
解:
(1) 按a升幂排列为
(2)按a降幂排列为
想一想:
如果是(1) 按b升幂排列 ; (2)按b降幂排列,结果回怎样呢?
例3、把多项式
按x升幂进行排列。
(1)重新排列多项式时,每一项一定要连同它的符号一起移动;
(2)含有两个或两个以上字母的多项式,常常按照其中某个字母升幂排列或降幂排列。
解:按x升幂排列是
思维升级
把 看成一个“字母”,把代数式
按“字母”(2x-y)的次数作升幂排列。若2x-y=3,试求这个代数式的值。
开放题
写一个含有字母x,y的多项式,满足下列条件:
①六次四项式。②每一项的系数是1或-1。③不
含常数项。④每一项必须同时含字母x,y,但不能
含其他字母。⑤按x的升幂排列。
本节课我们学了什么?
升幂排列,降幂排列。
P104习题3.3第5,6题
爱数学
爱数学周报
再见
3.升幂排列和降幂排列
华东师大版七年级(上册)
次数:所有字母的指数的和。
系数:单项式中的数字因数。
项:式中的每个单项式叫多项式的项。
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数。
整式
成长的足迹
1. 单项式m2n2的系数是_______,
次数是______, m2n2是____次单项式.
2. 多项式x+y-z是单项式 , ,___的和,它是___次___项式.
3. 多项式3m3-2m-5+m2的常数项是____,
一次项是_____, 二次项的系数是_____.
1
4
4
x
y
-z
1
3
-2m
-2
4.如果-5xym-1为4次单项式,则m=____.
4
5.若-ax2yb+1是关于x、y的五次单项式,且系数为-1/2,则a= ,b= .
1/2
2
6.下列说法中,正确的是( )
D
成长的足迹
8、(1)买单价为a元的笔记本m本,付出20元,应找回_______元.
(20-am)
(2)用字母表示图形中的黑色部分面积是________
a
3
m
m
3a-m2
7、判断题:
(1)-5ab2的系数是5( )
(2)xy2的系数是0( )
(3) 的系数是 ( )
(4)-ab2c的次数是2( )
×
×
×
×
9.下列式子中哪些是单项式,哪些是多项式,哪些是整式
10.己知多项式
不含x3项和x2项,求当x=-1时这个多项式的值.
解:根据题意,有
{
{
∴
∴
原多项式为
当x=-1时,
11.已知代数式3xn-(m-1)x+1是关于x的三次二项式,求m、n的值。
12. 是 次 项式,其中三次项系数是 ,二次项为 ,常数项为 ,写出所有的项 。
三
三
多项式x +x+1的项是_____
问题1.如果交换多项式各项位置,所得到
的多项式与原多项式是否相等?为什么?
相等(加法交换律)
问题2.任意交换x +x+1中各项的位置,可以得到几种不同的排列方式?请一一列举出来.
可以得到6种不同的排列方式,即x +x+1, x+x +1, x+1+x , x +1+x, 1+x+ x , 1+x +x.
问题3.以上六种排列中,你认为哪几种比较整齐?
x +x+1 ,1+x+ x 这样的排列比较整齐.
问题4.你认为是什么特点使得两种排列比较整齐呢?
这两种排列有一个共同特点,那就是x的指数是逐渐变小(或变大)的.
这样整齐的写法除了美观之外,还会为今后的计算带来方便。因而我们常常把一个多项式各项的位置按照其中某一个字母的指数大小顺序来排列.
例如把多项式 按x的指数从大到小的顺序排列是 ,按x指数从小到大的顺序排列是 .
降幂排列:把一个多项式按某个字母的指数按从大到小的顺序排列起来,叫做把多项式按这个字母降幂排列。
升幂排列:把一个多项式按某个字母的指数按从小到大的顺序排列起来,叫做把多项式按这个字母升幂排列。
如 是按x的降幂排列
如 是按x的升幂排列
提问:
1. x +x+1是按x的____排列.
2. 1+x+x 是按x的____排列.
降幂
升幂
例1、把多项式
按r升幂进行排列。
解:按r升幂进行排列是:
注意
交换位置时,符号跟项走,第一项系数为正数时,正号可以省略.
例2:把多项式 重新排列.
注意:
含有两个或两个以上字母的多项式,常常按照其中某一字母升幂或降幂排列.
(1) 按a升幂排列 ; (2)按a降幂排列
解:
(1) 按a升幂排列为
(2)按a降幂排列为
想一想:
如果是(1) 按b升幂排列 ; (2)按b降幂排列,结果回怎样呢?
例3、把多项式
按x升幂进行排列。
(1)重新排列多项式时,每一项一定要连同它的符号一起移动;
(2)含有两个或两个以上字母的多项式,常常按照其中某个字母升幂排列或降幂排列。
解:按x升幂排列是
思维升级
把 看成一个“字母”,把代数式
按“字母”(2x-y)的次数作升幂排列。若2x-y=3,试求这个代数式的值。
开放题
写一个含有字母x,y的多项式,满足下列条件:
①六次四项式。②每一项的系数是1或-1。③不
含常数项。④每一项必须同时含字母x,y,但不能
含其他字母。⑤按x的升幂排列。
本节课我们学了什么?
升幂排列,降幂排列。
P104习题3.3第5,6题
爱数学
爱数学周报
再见
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
