七年级数学11.2 三角形全等的判定(HL)
文档属性
| 名称 | 七年级数学11.2 三角形全等的判定(HL) |  | |
| 格式 | zip | ||
| 文件大小 | 297.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-16 19:54:16 | ||
图片预览


文档简介
(共18张PPT)
三角形全等的判定(HL)
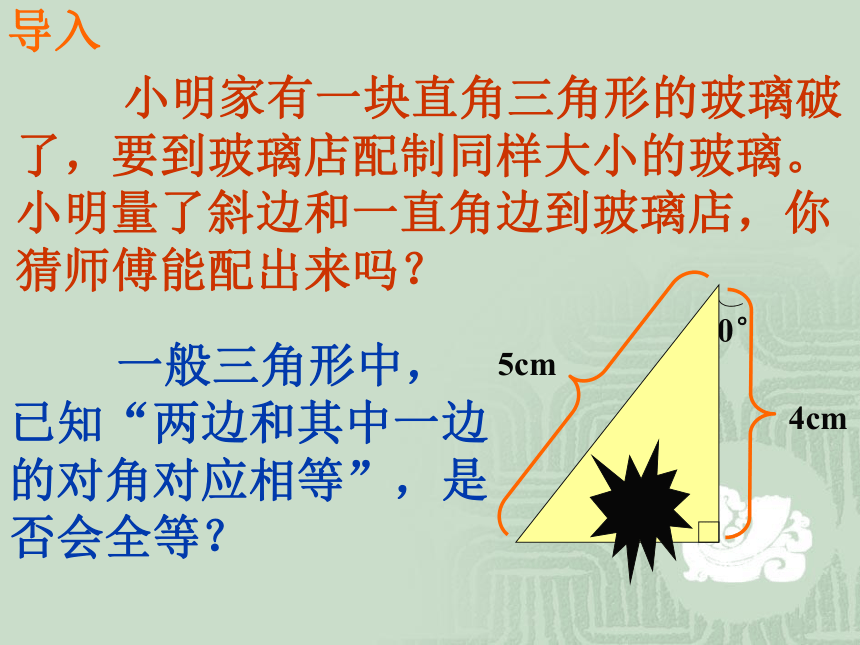
导入
小明家有一块直角三角形的玻璃破
了,要到玻璃店配制同样大小的玻璃。
小明量了斜边和一直角边到玻璃店,你
猜师傅能配出来吗?
5cm
80°
4cm
一般三角形中,
已知“两边和其中一边
的对角对应相等”,是
否会全等?
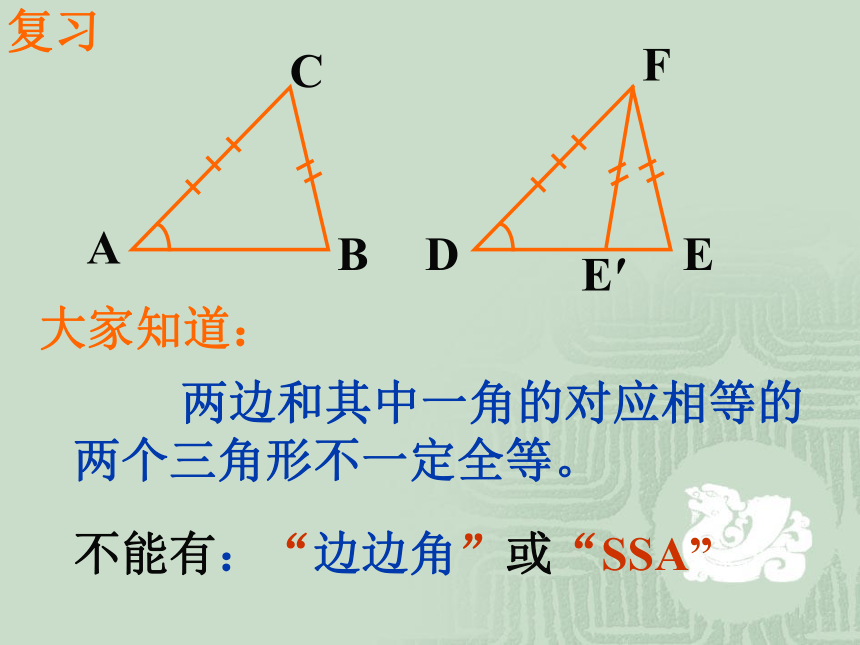
复习
大家知道:
两边和其中一角的对应相等的
两个三角形不一定全等。
不能有:“边边角”或“SSA”
A
B
C
D
E
F
E′
探究
你能画一个斜边为5cm,一直角边
为4cm的直角三角形吗?
Ⅰ.画∠MCN=90°;
Ⅱ.在射线CN上截取CA=4cm;
Ⅲ.以A为圆心,5cm为半径画弧,交CM
于点B;
同桌交流:你们画的三角形有什么
关系?
Ⅳ.连接AB。
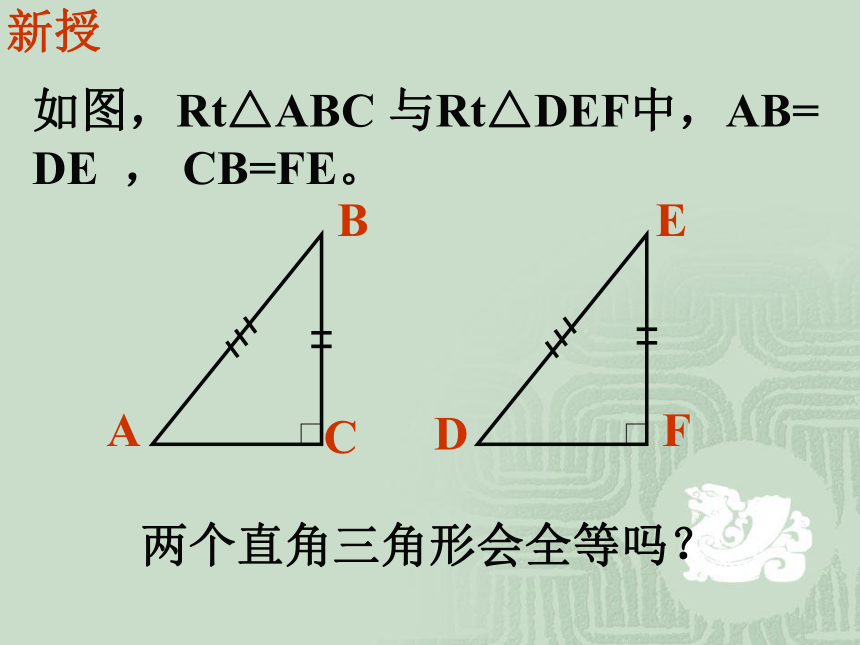
新授
如图,Rt△ABC 与Rt△DEF中,AB=
DE , CB=FE。
两个直角三角形会全等吗?
A
B
C
D
E
F
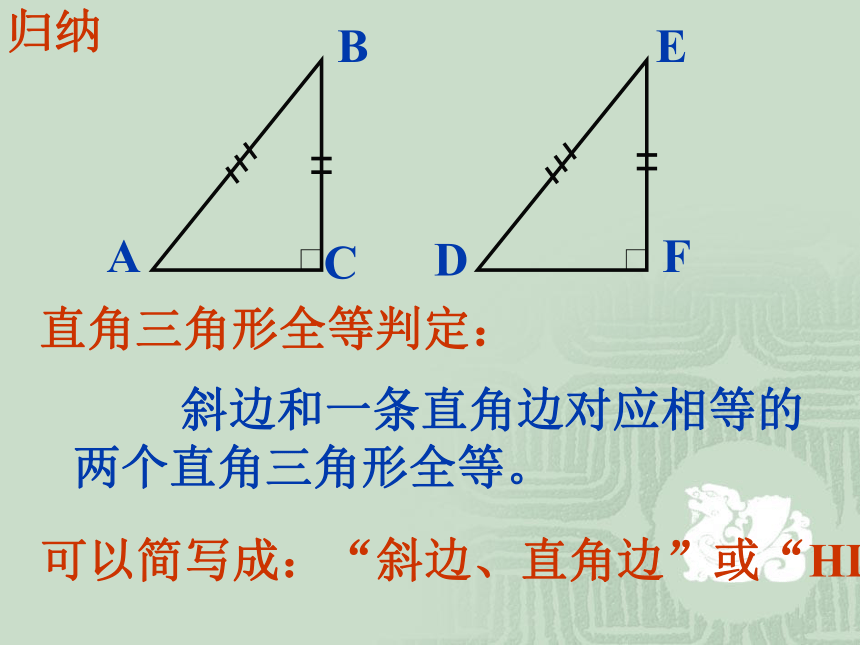
归纳
直角三角形全等判定:
斜边和一条直角边对应相等的两个直角三角形全等。
可以简写成:“斜边、直角边”或“HL”
A
B
C
D
E
F
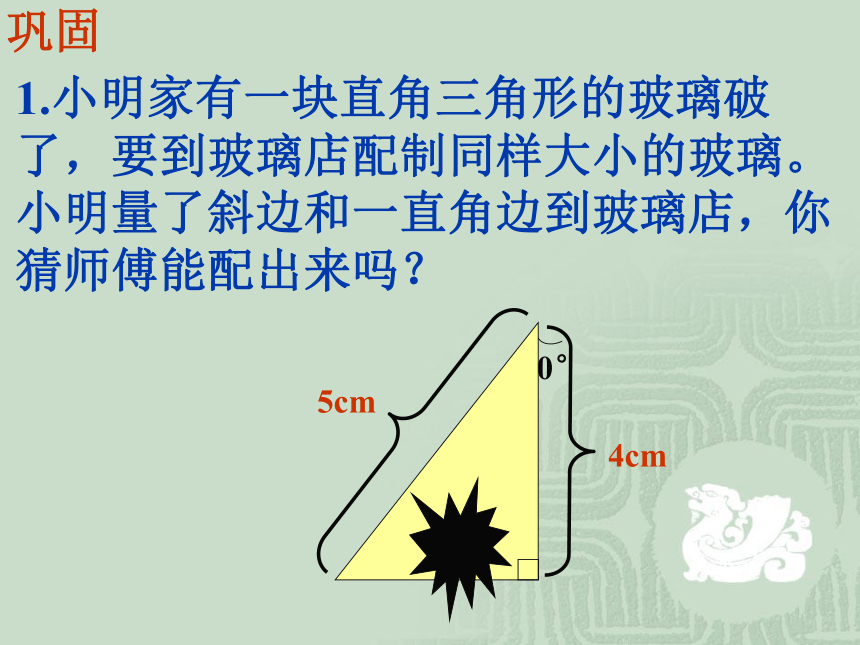
巩固
1.小明家有一块直角三角形的玻璃破
了,要到玻璃店配制同样大小的玻璃。
小明量了斜边和一直角边到玻璃店,你
猜师傅能配出来吗?
5cm
80°
4cm
巩固
2. Rt△ABC与Rt△DEF的各边如图所
示,那么Rt△ABC与Rt△DEF全等吗?
为什么?
A
B
C
F
E
6cm
6cm
D
注意:字母的对应位置。
4cm
4cm
3.如图,C是路段AB的中点,两人从C点同时出发,以相同的速度沿两条直线行走,并同时到达D、E两地。DA⊥AB,EB⊥AB ,D 、E与路段AB
的距离相等吗?
为什么?
巩固
A
B
D
C
E
范例
例1.如图,AC⊥BC,BD⊥AD,AC=BD。
求证:BC=AD。
根据条件选择合适的三角形
方法:
A
B
C
D
公共边
隐含条件:
巩固
4.如图,已知AB=CD,AE⊥BC,DF⊥
BC,CE=BF。
求证:AE=DF。
部分共边
隐含条件:
D
A
B
C
F
E
巩固
5.如图,已知在Rt△ABC与Rt△A'B'C'
中∠C=∠C'=90°,AC=A'C',BC=
B'C',则Rt△ABC与Rt△A'B'C'全等的
根据是( )
A HL
B ASA
C SAS
D SSA
直角三角形判定:SSS, SAS,
ASA(AAS), HL
A
B
C
A'
B'
C'
例2.如图,∠ABD=∠ACD=90°,BD=CD,AD与BC相交于点E。
求证:BE=CE。
范例
A
B
C
D
E
巩固
6.已知:如图,点P在线段AB上,
AC⊥AB于A, DB⊥AB于B,PC=
PD,AC=PB。
求证:PC⊥PD 。
P
A
C
D
B
小结
2、隐含条件的找法
1、直角三角形全等判定:
3、直角三角形全等判定的应用:
通过证明直角三角形全等,从而证明相关的边相等或角相等
公共边或部分共边
HL,
SSS,SAS,ASA(AAS)
作业
1.如图,在△ABC中,D是BC的中点,
DE⊥AB于E, DF⊥AC于F,且BE=
CF。
求证:AD平分∠BAC。
A
B
C
D
E
F
巩固
2.已知:如图,已知AE是△ABC的高,
D 为AC上一点,AE交BD于点F,且FE=CE,BF=AC。
求证:BD⊥AC。
B
A
F
D
E
C
三角形全等的判定(HL)
导入
小明家有一块直角三角形的玻璃破
了,要到玻璃店配制同样大小的玻璃。
小明量了斜边和一直角边到玻璃店,你
猜师傅能配出来吗?
5cm
80°
4cm
一般三角形中,
已知“两边和其中一边
的对角对应相等”,是
否会全等?
复习
大家知道:
两边和其中一角的对应相等的
两个三角形不一定全等。
不能有:“边边角”或“SSA”
A
B
C
D
E
F
E′
探究
你能画一个斜边为5cm,一直角边
为4cm的直角三角形吗?
Ⅰ.画∠MCN=90°;
Ⅱ.在射线CN上截取CA=4cm;
Ⅲ.以A为圆心,5cm为半径画弧,交CM
于点B;
同桌交流:你们画的三角形有什么
关系?
Ⅳ.连接AB。
新授
如图,Rt△ABC 与Rt△DEF中,AB=
DE , CB=FE。
两个直角三角形会全等吗?
A
B
C
D
E
F
归纳
直角三角形全等判定:
斜边和一条直角边对应相等的两个直角三角形全等。
可以简写成:“斜边、直角边”或“HL”
A
B
C
D
E
F
巩固
1.小明家有一块直角三角形的玻璃破
了,要到玻璃店配制同样大小的玻璃。
小明量了斜边和一直角边到玻璃店,你
猜师傅能配出来吗?
5cm
80°
4cm
巩固
2. Rt△ABC与Rt△DEF的各边如图所
示,那么Rt△ABC与Rt△DEF全等吗?
为什么?
A
B
C
F
E
6cm
6cm
D
注意:字母的对应位置。
4cm
4cm
3.如图,C是路段AB的中点,两人从C点同时出发,以相同的速度沿两条直线行走,并同时到达D、E两地。DA⊥AB,EB⊥AB ,D 、E与路段AB
的距离相等吗?
为什么?
巩固
A
B
D
C
E
范例
例1.如图,AC⊥BC,BD⊥AD,AC=BD。
求证:BC=AD。
根据条件选择合适的三角形
方法:
A
B
C
D
公共边
隐含条件:
巩固
4.如图,已知AB=CD,AE⊥BC,DF⊥
BC,CE=BF。
求证:AE=DF。
部分共边
隐含条件:
D
A
B
C
F
E
巩固
5.如图,已知在Rt△ABC与Rt△A'B'C'
中∠C=∠C'=90°,AC=A'C',BC=
B'C',则Rt△ABC与Rt△A'B'C'全等的
根据是( )
A HL
B ASA
C SAS
D SSA
直角三角形判定:SSS, SAS,
ASA(AAS), HL
A
B
C
A'
B'
C'
例2.如图,∠ABD=∠ACD=90°,BD=CD,AD与BC相交于点E。
求证:BE=CE。
范例
A
B
C
D
E
巩固
6.已知:如图,点P在线段AB上,
AC⊥AB于A, DB⊥AB于B,PC=
PD,AC=PB。
求证:PC⊥PD 。
P
A
C
D
B
小结
2、隐含条件的找法
1、直角三角形全等判定:
3、直角三角形全等判定的应用:
通过证明直角三角形全等,从而证明相关的边相等或角相等
公共边或部分共边
HL,
SSS,SAS,ASA(AAS)
作业
1.如图,在△ABC中,D是BC的中点,
DE⊥AB于E, DF⊥AC于F,且BE=
CF。
求证:AD平分∠BAC。
A
B
C
D
E
F
巩固
2.已知:如图,已知AE是△ABC的高,
D 为AC上一点,AE交BD于点F,且FE=CE,BF=AC。
求证:BD⊥AC。
B
A
F
D
E
C
