15.2分式的运算 同步练习-2021-2022学年人教版数学八年级上册(Word版含答案)
文档属性
| 名称 | 15.2分式的运算 同步练习-2021-2022学年人教版数学八年级上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 174.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 19:47:25 | ||
图片预览



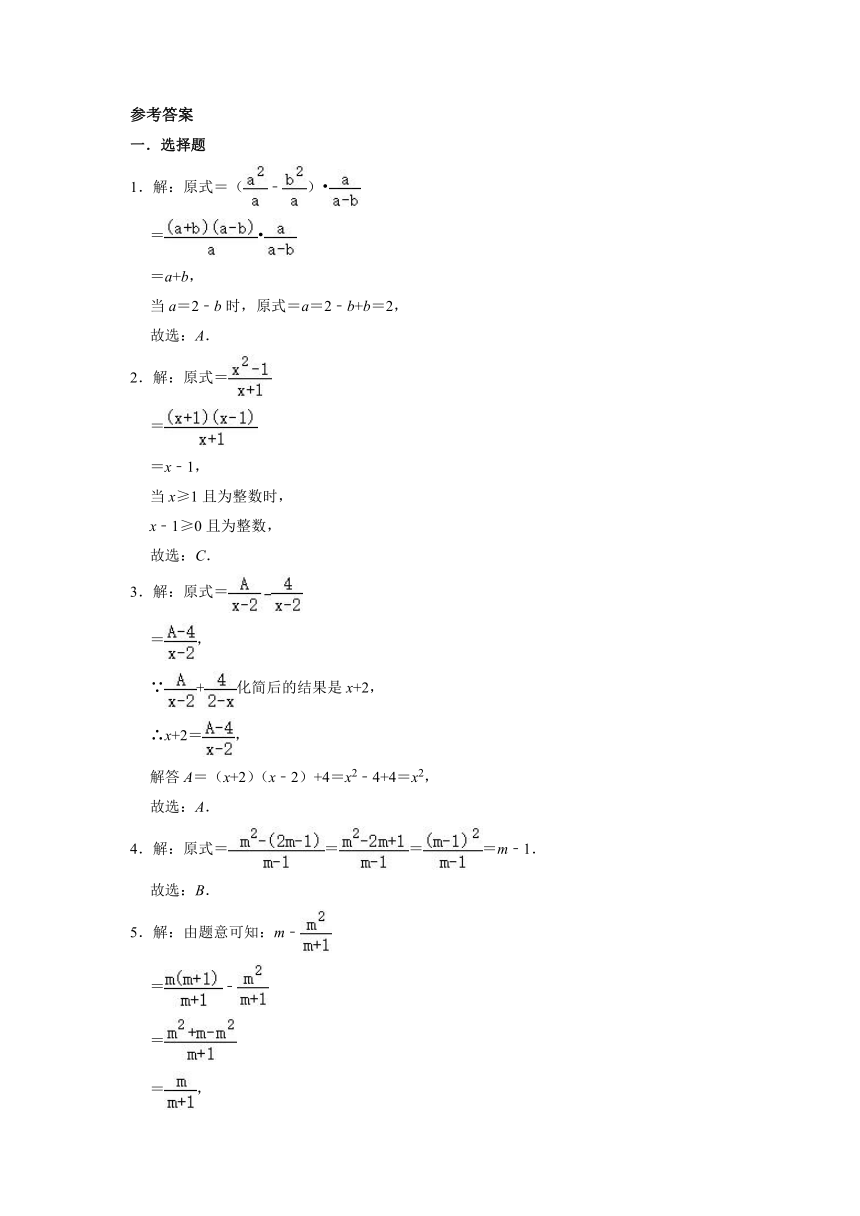
文档简介
15.2分式的运算
一.选择题
1.当a=2﹣b时,计算()的值为( )
A.2 B.﹣2 C. D.
2.若x为正整数,则计算的结果是( )
A.正整数 B.负整数 C.非负整数 D.非正整数
3.如果分式+化简后的结果是x+2,则A表示的整式( )
A.x2 B.x2+4x+8 C.x2﹣8 D.﹣x2
4.计算的结果是( )
A.m+1 B.m﹣1 C.m﹣2 D.﹣m﹣2
5.在计算÷时,把运算符号“÷”看成了“+”,得到的计算结果是m,则这道题正确的结果是( )
A.m B. C.m﹣1 D.
6.中国抗疫取得了巨大成就,堪称奇迹,为世界各国防控疫情提供了重要借鉴和支持,让中国人民倍感自豪.2020年1月12日,世界卫生组织正式将2019新型冠状病毒命名为2019﹣nCoV.该病毒的直径在0.00000008米~0.00000012米,将0.00000012用科学记数法表示为( )
A.12×10﹣7 B.1.2×10﹣6 C.1.2×10﹣7 D.0.12×10﹣6
7.如果m2+3m﹣1=0,那么代数式(m﹣) 的值是( )
A.﹣3 B.﹣1 C.1 D.3
8.嘉嘉在做“先化简,再求值:,其中x=1.”时,误将2x+3中2x前的系数2漏掉,那么他的计算结果与正确结果( )
A.相等 B.相差 C.和为0 D.积为﹣1
9.化简的结果为,则M为( )
A. B. C. D.
10.已知x﹣=1,则的值是( )
A. B. C. D.
二.填空题
11.计算 (1﹣)÷(a﹣b)= .
12.计算的结果是 .
13.(x+2+)÷= .
14.化简:的结果为 ;= .
15.若+=2,则= .
三.解答题
16.计算:
(1);
(2).
17.小蕊在作业本上写完一个代数式的正确计算过程,不小心墨水洒了,遮住了原代数式的一部分(被墨水遮住的部分用△代替),该式为.
(1)求被墨水遮住部分的代数式;
(2)原代数式的值能等于﹣1吗?请说明理由.
18.如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这个分式为“和谐分式”.
(1)下列分式:①;②;③,其中是“和谐分式”的是 (填写序号即可);
(2)若a为整数,且为“和谐分式”,写出满足条件的a的值为 ;
(3)在化简时,小明和小娟分别进行了如下三步变形:
小明:原式==,
小娟:原式=﹣==,
你比较欣赏谁的做法?先进行选择,再根据你的选择完成化简过程,并说明你选择的理由.
参考答案
一.选择题
1.解:原式=(﹣)
=
=a+b,
当a=2﹣b时,原式=a=2﹣b+b=2,
故选:A.
2.解:原式=
=
=x﹣1,
当x≥1且为整数时,
x﹣1≥0且为整数,
故选:C.
3.解:原式=
=,
∵+化简后的结果是x+2,
∴x+2=,
解答A=(x+2)(x﹣2)+4=x2﹣4+4=x2,
故选:A.
4.解:原式====m﹣1.
故选:B.
5.解:由题意可知:m﹣
=﹣
=
=,
∴÷
=
=m,
故选:A.
6.解:将0.00000012用科学记数法表示为1.2×10﹣7.
故选:C.
7.解:原式=,
=,
=,
=(m+3)m,
=m2+3m,
∵m2+3m﹣1=0,
∴m2+3m=1,
故选:C.
8.解:﹣
=﹣
=﹣,
当x=1时,原式=﹣=﹣,
﹣
=﹣
=,
当x=1时,原式==﹣1,
﹣1﹣(﹣)=,
∴计算结果与正确结果相差,
故选:B.
9.解:由题意得,M=﹣=﹣==.
故选:C.
10.解:∵x﹣=1,
∴(x﹣)2=1,
∴x2+=3,
原式的倒数为,
∴原式=,
故选:C.
二.填空题
11.解:原式=()
=
=,
故答案为:.
12.解:原式=
=,
故答案为:.
13.解:原式=[]÷
=÷
=
=﹣,
故答案为;﹣.
14.解:x÷
=x
=.
=÷
=÷
=
=.
故答案为:,.
15.解:由题意可知:x+y=2xy,
∴原式=
=
=
=,
故答案为:.
三.解答题
16.解:(1)原式=
=﹣;
(2)原式=
=
=
=.
17.解:(1)∵,
∴被墨水遮住部分的代数式是 +
=﹣
=;
(2)原代数式的值不能等于﹣1,
理由是:=﹣1,
x+1=﹣(x﹣1),
解得:x=0,
要使分式(﹣)÷有意义,必须x﹣1≠0且x+1≠0且x≠0,
即x不能为1,﹣1,0,
所以原代数式的值不能等于﹣1.
18.解:(1)①分子或分母都不可以因式分解,不符合题意;
②分母可以因式分解,且这个分式不可约分,符合题意;
③这个分式可以约分,不符合题意;
故答案为:②;
(2)将分母变成完全平方公式得:x2±4x+4,此时a=±4;
将分母变形成(x+1)(x+4),此时a=5;
故答案为:±4或5;
(3)我欣赏小娟的做法,
原式=
=
=,
理由:小娟利用了和谐分式,通分时找到了最简公分母.
一.选择题
1.当a=2﹣b时,计算()的值为( )
A.2 B.﹣2 C. D.
2.若x为正整数,则计算的结果是( )
A.正整数 B.负整数 C.非负整数 D.非正整数
3.如果分式+化简后的结果是x+2,则A表示的整式( )
A.x2 B.x2+4x+8 C.x2﹣8 D.﹣x2
4.计算的结果是( )
A.m+1 B.m﹣1 C.m﹣2 D.﹣m﹣2
5.在计算÷时,把运算符号“÷”看成了“+”,得到的计算结果是m,则这道题正确的结果是( )
A.m B. C.m﹣1 D.
6.中国抗疫取得了巨大成就,堪称奇迹,为世界各国防控疫情提供了重要借鉴和支持,让中国人民倍感自豪.2020年1月12日,世界卫生组织正式将2019新型冠状病毒命名为2019﹣nCoV.该病毒的直径在0.00000008米~0.00000012米,将0.00000012用科学记数法表示为( )
A.12×10﹣7 B.1.2×10﹣6 C.1.2×10﹣7 D.0.12×10﹣6
7.如果m2+3m﹣1=0,那么代数式(m﹣) 的值是( )
A.﹣3 B.﹣1 C.1 D.3
8.嘉嘉在做“先化简,再求值:,其中x=1.”时,误将2x+3中2x前的系数2漏掉,那么他的计算结果与正确结果( )
A.相等 B.相差 C.和为0 D.积为﹣1
9.化简的结果为,则M为( )
A. B. C. D.
10.已知x﹣=1,则的值是( )
A. B. C. D.
二.填空题
11.计算 (1﹣)÷(a﹣b)= .
12.计算的结果是 .
13.(x+2+)÷= .
14.化简:的结果为 ;= .
15.若+=2,则= .
三.解答题
16.计算:
(1);
(2).
17.小蕊在作业本上写完一个代数式的正确计算过程,不小心墨水洒了,遮住了原代数式的一部分(被墨水遮住的部分用△代替),该式为.
(1)求被墨水遮住部分的代数式;
(2)原代数式的值能等于﹣1吗?请说明理由.
18.如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这个分式为“和谐分式”.
(1)下列分式:①;②;③,其中是“和谐分式”的是 (填写序号即可);
(2)若a为整数,且为“和谐分式”,写出满足条件的a的值为 ;
(3)在化简时,小明和小娟分别进行了如下三步变形:
小明:原式==,
小娟:原式=﹣==,
你比较欣赏谁的做法?先进行选择,再根据你的选择完成化简过程,并说明你选择的理由.
参考答案
一.选择题
1.解:原式=(﹣)
=
=a+b,
当a=2﹣b时,原式=a=2﹣b+b=2,
故选:A.
2.解:原式=
=
=x﹣1,
当x≥1且为整数时,
x﹣1≥0且为整数,
故选:C.
3.解:原式=
=,
∵+化简后的结果是x+2,
∴x+2=,
解答A=(x+2)(x﹣2)+4=x2﹣4+4=x2,
故选:A.
4.解:原式====m﹣1.
故选:B.
5.解:由题意可知:m﹣
=﹣
=
=,
∴÷
=
=m,
故选:A.
6.解:将0.00000012用科学记数法表示为1.2×10﹣7.
故选:C.
7.解:原式=,
=,
=,
=(m+3)m,
=m2+3m,
∵m2+3m﹣1=0,
∴m2+3m=1,
故选:C.
8.解:﹣
=﹣
=﹣,
当x=1时,原式=﹣=﹣,
﹣
=﹣
=,
当x=1时,原式==﹣1,
﹣1﹣(﹣)=,
∴计算结果与正确结果相差,
故选:B.
9.解:由题意得,M=﹣=﹣==.
故选:C.
10.解:∵x﹣=1,
∴(x﹣)2=1,
∴x2+=3,
原式的倒数为,
∴原式=,
故选:C.
二.填空题
11.解:原式=()
=
=,
故答案为:.
12.解:原式=
=,
故答案为:.
13.解:原式=[]÷
=÷
=
=﹣,
故答案为;﹣.
14.解:x÷
=x
=.
=÷
=÷
=
=.
故答案为:,.
15.解:由题意可知:x+y=2xy,
∴原式=
=
=
=,
故答案为:.
三.解答题
16.解:(1)原式=
=﹣;
(2)原式=
=
=
=.
17.解:(1)∵,
∴被墨水遮住部分的代数式是 +
=﹣
=;
(2)原代数式的值不能等于﹣1,
理由是:=﹣1,
x+1=﹣(x﹣1),
解得:x=0,
要使分式(﹣)÷有意义,必须x﹣1≠0且x+1≠0且x≠0,
即x不能为1,﹣1,0,
所以原代数式的值不能等于﹣1.
18.解:(1)①分子或分母都不可以因式分解,不符合题意;
②分母可以因式分解,且这个分式不可约分,符合题意;
③这个分式可以约分,不符合题意;
故答案为:②;
(2)将分母变成完全平方公式得:x2±4x+4,此时a=±4;
将分母变形成(x+1)(x+4),此时a=5;
故答案为:±4或5;
(3)我欣赏小娟的做法,
原式=
=
=,
理由:小娟利用了和谐分式,通分时找到了最简公分母.
