2020-2021学年华东师大版九年级数学下册第27章圆 达标检测卷(word版含答案)
文档属性
| 名称 | 2020-2021学年华东师大版九年级数学下册第27章圆 达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 393.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 22:59:59 | ||
图片预览



文档简介
第27章达标检测卷
一、选择题(每题3分,共30分)
1.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A.点P在⊙O外 B.点P在⊙O内 C.点P在⊙O上 D.无法确定
2.如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( )
A.8 B.4 C.10 D.5
3.给出下列四个结论,其中正确的结论为( )
A.三点确定一个圆
B.直径是最长的弦
C.圆周角是圆心角的一半
D.长度相等的弧是等弧
4.如图,在⊙O中,CD⊥AB,∠A=58°,则∠BOD等于( )
A.58° B.32° C.116° D.64°
5.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠A=30°,则⊙O的半径是( )
A.1 B.2 C. D.
6.如果一个扇形的半径是3,弧长是π,那么此扇形的圆心角的度数为( )
A.30° B.45° C.60° D.90°
7.如图,在Rt△ABC中,∠A=90°,BC=2,以BC的中点O为圆心的圆分别与AB,AC相切于D,E两点,则的长为( )
A. B. C.π D.2π
8.如图,在边长为2的正方形ABCD中,先以点D为圆心,DA为半径画,再以BC为直径画半圆.若阴影部分①的面积为S1,阴影部分②的面积为S2,则S2-S1的值为( )
A.-4 B.+4 C.-4 D.+2
9.已知一弧长为l的弧所对的圆心角为120°,那么它所对的弦长为( )
A.l B.l C.l D.l
10.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边都相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边都相切……按这样的规律进行下去,正六边形A10B10C10D10E10F10的边长为( )
A. B. C. D.
二、填空题(每题3分,共24分)
11.如图,点A,B,C在⊙O上,∠AOC=60°,则∠ABC的度数是________.
12.如图,已知⊙O的半径为3,点O到直线l的距离OA=5,将直线l沿射线AO方向平移m个单位后,⊙O与直线l相切,则m=________.
13.如图,AD为⊙O的直径,AD=6 cm,∠DAC=∠ABC,则AC=________.
14.直角三角形的两边长分别为16和12,则此直角三角形的外接圆的半径是________.
15.如图,PA,PB是⊙O的切线,切点分别为A,B,直线EF也是⊙O的切线,Q是切点,分别交PA,PB于点E,F.若∠APB=50°,则∠EOF的度数为________.
16.一个圆锥形漏斗,某同学测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为________.
17.太极是中国文化史上的一个重要概念.如图所示的太极图是先以AB为直径作一个大圆⊙O,再以OB,OA为直径分别向左、向右作两个半圆而成.若AB=10 cm,记,,的长分别为l1,l2,l3,则l1+l2+l3=________cm.
18.中国魏晋时期的数学家刘徽首创“割圆术”,奠定了中国圆周率计算在世界上的领先地位.刘徽提出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”,由此求得圆周率π的近似值.如图,设半径为r的圆内接正n边形的周长为C,圆的直径为d,当n=6时,π≈==3,则当n=12时,π≈≈________.(结果精确到0.01,参考数据:sin 15°=cos 75°≈0.259,sin 75°=cos 15°≈0.966)
三、解答题(19、20题每题10分,21、22题每题11分,23、24题每题12分,共66分)
19.如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上,连结DE,BE.
(1)若∠AOD=60°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
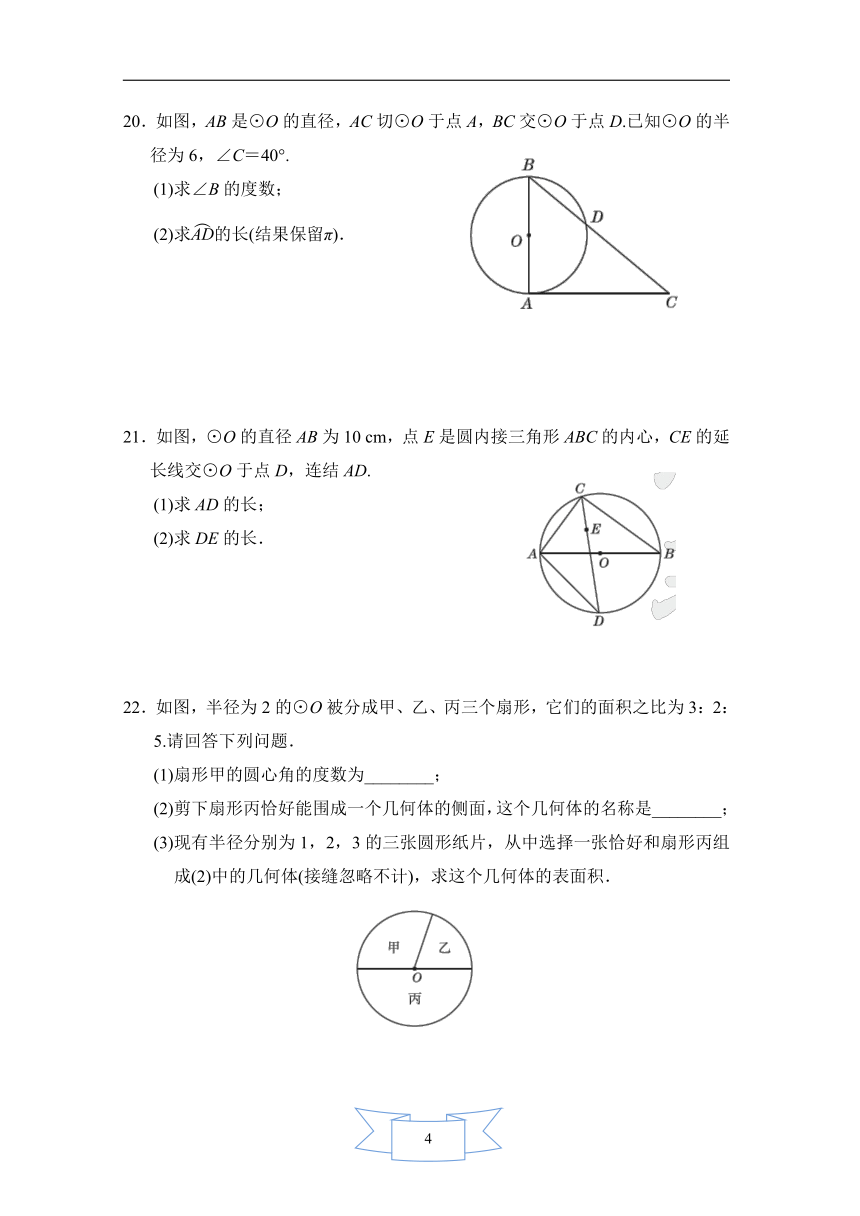
20.如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于点D.已知⊙O的半径为6,∠C=40°.
(1)求∠B的度数;
(2)求的长(结果保留π).
21.如图,⊙O的直径AB为10 cm,点E是圆内接三角形ABC的内心,CE的延长线交⊙O于点D,连结AD.
(1)求AD的长;
(2)求DE的长.
22.如图,半径为2的⊙O被分成甲、乙、丙三个扇形,它们的面积之比为3:2:5.请回答下列问题.
(1)扇形甲的圆心角的度数为________;
(2)剪下扇形丙恰好能围成一个几何体的侧面,这个几何体的名称是________;
(3)现有半径分别为1,2,3的三张圆形纸片,从中选择一张恰好和扇形丙组成(2)中的几何体(接缝忽略不计),求这个几何体的表面积.
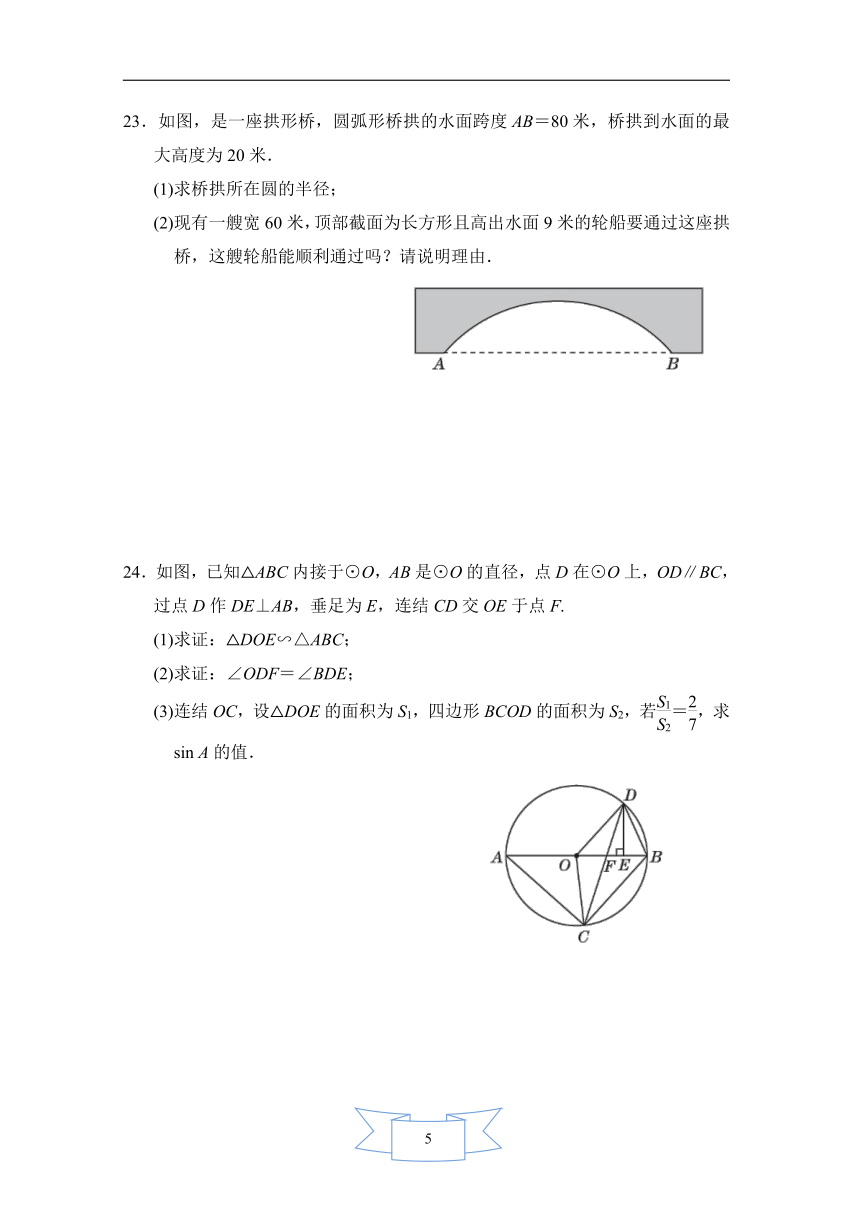
23.如图,是一座拱形桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.
(1)求桥拱所在圆的半径;
(2)现有一艘宽60米,顶部截面为长方形且高出水面9米的轮船要通过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
24.如图,已知△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连结CD交OE于点F.
(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连结OC,设△DOE的面积为S1,四边形BCOD的面积为S2,若=,求sin A的值.
答案
一、1.A
2.D
3.B
4.D
5.A 点拨:本题运用数形结合思想.如图,过点B作直径BB′,连结B′C,则∠B′=∠A=30°,∠B′CB=90°,∴BC=B′B,∴B′B=2×1=2,故⊙O的半径是1.
6.C
7.B 点拨:如图,连结OD、OE.设⊙O的半径为r.∵⊙O分别与AB、AC相切于D、E两点,∴OE⊥AC,OD⊥AB.∵∠A=90°,∴∠DOE=90°,OD∥AC.∵点O是BC的中点,∴OD是△ABC的中位线,∴OD=AC,∴AC=2r.同理可得AB=2r.∴AB=AC.又∵∠A=90°,∴∠B=45°.∵BC=2,∴由勾股定理可得AB=2,∴r=1,∴的长为=,故选B.
8.A 点拨:由题图可知,扇形ADC的面积+半圆形BC的面积+阴影部分①的面积-正方形ABCD的面积=阴影部分②的面积,∴S2-S1=扇形ADC的面积+半圆形BC的面积-正方形ABCD的面积=+π-22=-4.
9.C 点拨:设该弧所在⊙O的半径为r,所对的弦为AB.如图,过点O作OC⊥AB于点C.∵∠AOB=120°,∴的长为=l,则r=l.∵∠AOB=120°,∴∠OBC=30°,∴OC=OB,∴BC==l,∴AB=2BC=l.
10.D 点拨:∵正六边形A1B1C1D1E1F1的边长为2=,∴正六边形A2B2C2D2E2F2的外接圆的半径为,则正六边形A2B2C2D2E2F2的边长为=.同理,正六边形A3B3C3D3E3F3的边长为=……正六边形AnBnCnDnEnFn的边长为.当n=10时,正六边形A10B10C10D10E10F10的边长为===,故选D.
二、11.150° 12.2或8
13.3 cm 14.8或10 15.65°
16.15π 17.10π
18.3.11 点拨:圆的内接正十二边形被半径分成12个如图所示的等腰三角形,其顶角为30°.作OH⊥AB于点H,则∠AOH=15°.∵AO=BO=r,∴在Rt△AOH中,sin∠AOH=,即sin 15°=,∴AH=r×sin 15°,AB=2AH=2r×sin 15°,∴C=12×2r×sin 15°=24r×sin 15°.又∵d=2r,∴π≈=≈3.11.
三、19.解:(1)∵OD⊥AB,∴=,
∴∠DEB=∠AOD=30°.
(2)在Rt△AOC中,OC=3,OA=5,由勾股定理得AC=4,
∴AB=2AC=8.
20.解:(1)∵AB是⊙O的直径,AC切⊙O于点A,
∴∠BAC=90°.
∵∠C=40°,∴∠B=50°.
(2)如图,连结OD.∵∠B=50°,
∴∠AOD=2∠B=100°,
∴的长为=π.
21.解:(1)如图,连结BD.
∵AB为⊙O的直径,
∴∠ACB=∠ADB=90°.
∵点E是圆内接三角形ABC的内心,
∴CE平分∠ACB,∴∠1=45°,
∴∠DBA=∠1=45°,
∴△ADB为等腰直角三角形,
∴AD=AB=×10=5(cm).
(2)如图,连结AE.
∵点E是圆内接三角形ABC的内心,
∴∠2=∠4.
∵∠1=∠5,∴∠3=∠1+∠2=∠5+∠4,
即∠3=∠DAE,∴DE=DA=5 cm.
22.解:(1)108°
(2)圆锥
(3)扇形丙的圆心角的度数为360°×=180°.
设剪下扇形丙能围成的圆锥的底面半径为x.根据题意,得2πx=,∴x=1,
∴选择半径为1的圆形纸片恰好和扇形丙组成(2)中的几何体,该几何体的表面积为π×12+=3π.
23.解:(1)如图,设点E是桥拱所在圆的圆心.
过点E作EF⊥AB于点F,延长EF交⊙E于点C,连结AE,
则CF=20米.由垂径定理知,F是AB的中点,
∴AF=FB=AB=40米.设桥拱所在圆的半径为r米,由勾股定理,
得AE2=AF2+EF2=AF2+(CE-CF)2,
即r2=402+(r-20)2,解得r=50.
∴桥拱所在圆的半径为50米.
(2)这艘轮船能顺利通过.理由如下:
如图,设MN=60米,MN∥AB,
EC与MN的交点为D,连结EM.
易知DE⊥MN,
∴MD=30米,
∴DE===40(米).
∵EF=EC-CF=50-20=30(米),
∴DF=DE-EF=40-30=10(米).
∵10米>9米,∴这艘轮船能顺利通过.
24.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°.∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB.
∵OD∥BC,∴∠DOE=∠ABC,
∴△DOE∽△ABC.
(2)证明:∵△DOE∽△ABC,
∴∠ODE=∠A.
∵∠A=∠BDC,∴∠ODE=∠BDC,
∴∠ODF=∠BDE.
(3)解:∵△DOE∽△ABC,
∴==,
即S△ABC=4S△DOE=4S1.
∵OA=OB,∴S△BOC=S△ABC,即S△BOC=2S1.
∵=,S2=S△BOC+S△DOE+S△DBE=2S1+S1+S△DBE,
∴S△DBE=S1,
∴BE=OE,即OE=OB=OD,
∴sin A=sin∠ODE==.
一、选择题(每题3分,共30分)
1.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A.点P在⊙O外 B.点P在⊙O内 C.点P在⊙O上 D.无法确定
2.如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( )
A.8 B.4 C.10 D.5
3.给出下列四个结论,其中正确的结论为( )
A.三点确定一个圆
B.直径是最长的弦
C.圆周角是圆心角的一半
D.长度相等的弧是等弧
4.如图,在⊙O中,CD⊥AB,∠A=58°,则∠BOD等于( )
A.58° B.32° C.116° D.64°
5.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠A=30°,则⊙O的半径是( )
A.1 B.2 C. D.
6.如果一个扇形的半径是3,弧长是π,那么此扇形的圆心角的度数为( )
A.30° B.45° C.60° D.90°
7.如图,在Rt△ABC中,∠A=90°,BC=2,以BC的中点O为圆心的圆分别与AB,AC相切于D,E两点,则的长为( )
A. B. C.π D.2π
8.如图,在边长为2的正方形ABCD中,先以点D为圆心,DA为半径画,再以BC为直径画半圆.若阴影部分①的面积为S1,阴影部分②的面积为S2,则S2-S1的值为( )
A.-4 B.+4 C.-4 D.+2
9.已知一弧长为l的弧所对的圆心角为120°,那么它所对的弦长为( )
A.l B.l C.l D.l
10.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边都相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边都相切……按这样的规律进行下去,正六边形A10B10C10D10E10F10的边长为( )
A. B. C. D.
二、填空题(每题3分,共24分)
11.如图,点A,B,C在⊙O上,∠AOC=60°,则∠ABC的度数是________.
12.如图,已知⊙O的半径为3,点O到直线l的距离OA=5,将直线l沿射线AO方向平移m个单位后,⊙O与直线l相切,则m=________.
13.如图,AD为⊙O的直径,AD=6 cm,∠DAC=∠ABC,则AC=________.
14.直角三角形的两边长分别为16和12,则此直角三角形的外接圆的半径是________.
15.如图,PA,PB是⊙O的切线,切点分别为A,B,直线EF也是⊙O的切线,Q是切点,分别交PA,PB于点E,F.若∠APB=50°,则∠EOF的度数为________.
16.一个圆锥形漏斗,某同学测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为________.
17.太极是中国文化史上的一个重要概念.如图所示的太极图是先以AB为直径作一个大圆⊙O,再以OB,OA为直径分别向左、向右作两个半圆而成.若AB=10 cm,记,,的长分别为l1,l2,l3,则l1+l2+l3=________cm.
18.中国魏晋时期的数学家刘徽首创“割圆术”,奠定了中国圆周率计算在世界上的领先地位.刘徽提出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”,由此求得圆周率π的近似值.如图,设半径为r的圆内接正n边形的周长为C,圆的直径为d,当n=6时,π≈==3,则当n=12时,π≈≈________.(结果精确到0.01,参考数据:sin 15°=cos 75°≈0.259,sin 75°=cos 15°≈0.966)
三、解答题(19、20题每题10分,21、22题每题11分,23、24题每题12分,共66分)
19.如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上,连结DE,BE.
(1)若∠AOD=60°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
20.如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于点D.已知⊙O的半径为6,∠C=40°.
(1)求∠B的度数;
(2)求的长(结果保留π).
21.如图,⊙O的直径AB为10 cm,点E是圆内接三角形ABC的内心,CE的延长线交⊙O于点D,连结AD.
(1)求AD的长;
(2)求DE的长.
22.如图,半径为2的⊙O被分成甲、乙、丙三个扇形,它们的面积之比为3:2:5.请回答下列问题.
(1)扇形甲的圆心角的度数为________;
(2)剪下扇形丙恰好能围成一个几何体的侧面,这个几何体的名称是________;
(3)现有半径分别为1,2,3的三张圆形纸片,从中选择一张恰好和扇形丙组成(2)中的几何体(接缝忽略不计),求这个几何体的表面积.
23.如图,是一座拱形桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.
(1)求桥拱所在圆的半径;
(2)现有一艘宽60米,顶部截面为长方形且高出水面9米的轮船要通过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
24.如图,已知△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连结CD交OE于点F.
(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连结OC,设△DOE的面积为S1,四边形BCOD的面积为S2,若=,求sin A的值.
答案
一、1.A
2.D
3.B
4.D
5.A 点拨:本题运用数形结合思想.如图,过点B作直径BB′,连结B′C,则∠B′=∠A=30°,∠B′CB=90°,∴BC=B′B,∴B′B=2×1=2,故⊙O的半径是1.
6.C
7.B 点拨:如图,连结OD、OE.设⊙O的半径为r.∵⊙O分别与AB、AC相切于D、E两点,∴OE⊥AC,OD⊥AB.∵∠A=90°,∴∠DOE=90°,OD∥AC.∵点O是BC的中点,∴OD是△ABC的中位线,∴OD=AC,∴AC=2r.同理可得AB=2r.∴AB=AC.又∵∠A=90°,∴∠B=45°.∵BC=2,∴由勾股定理可得AB=2,∴r=1,∴的长为=,故选B.
8.A 点拨:由题图可知,扇形ADC的面积+半圆形BC的面积+阴影部分①的面积-正方形ABCD的面积=阴影部分②的面积,∴S2-S1=扇形ADC的面积+半圆形BC的面积-正方形ABCD的面积=+π-22=-4.
9.C 点拨:设该弧所在⊙O的半径为r,所对的弦为AB.如图,过点O作OC⊥AB于点C.∵∠AOB=120°,∴的长为=l,则r=l.∵∠AOB=120°,∴∠OBC=30°,∴OC=OB,∴BC==l,∴AB=2BC=l.
10.D 点拨:∵正六边形A1B1C1D1E1F1的边长为2=,∴正六边形A2B2C2D2E2F2的外接圆的半径为,则正六边形A2B2C2D2E2F2的边长为=.同理,正六边形A3B3C3D3E3F3的边长为=……正六边形AnBnCnDnEnFn的边长为.当n=10时,正六边形A10B10C10D10E10F10的边长为===,故选D.
二、11.150° 12.2或8
13.3 cm 14.8或10 15.65°
16.15π 17.10π
18.3.11 点拨:圆的内接正十二边形被半径分成12个如图所示的等腰三角形,其顶角为30°.作OH⊥AB于点H,则∠AOH=15°.∵AO=BO=r,∴在Rt△AOH中,sin∠AOH=,即sin 15°=,∴AH=r×sin 15°,AB=2AH=2r×sin 15°,∴C=12×2r×sin 15°=24r×sin 15°.又∵d=2r,∴π≈=≈3.11.
三、19.解:(1)∵OD⊥AB,∴=,
∴∠DEB=∠AOD=30°.
(2)在Rt△AOC中,OC=3,OA=5,由勾股定理得AC=4,
∴AB=2AC=8.
20.解:(1)∵AB是⊙O的直径,AC切⊙O于点A,
∴∠BAC=90°.
∵∠C=40°,∴∠B=50°.
(2)如图,连结OD.∵∠B=50°,
∴∠AOD=2∠B=100°,
∴的长为=π.
21.解:(1)如图,连结BD.
∵AB为⊙O的直径,
∴∠ACB=∠ADB=90°.
∵点E是圆内接三角形ABC的内心,
∴CE平分∠ACB,∴∠1=45°,
∴∠DBA=∠1=45°,
∴△ADB为等腰直角三角形,
∴AD=AB=×10=5(cm).
(2)如图,连结AE.
∵点E是圆内接三角形ABC的内心,
∴∠2=∠4.
∵∠1=∠5,∴∠3=∠1+∠2=∠5+∠4,
即∠3=∠DAE,∴DE=DA=5 cm.
22.解:(1)108°
(2)圆锥
(3)扇形丙的圆心角的度数为360°×=180°.
设剪下扇形丙能围成的圆锥的底面半径为x.根据题意,得2πx=,∴x=1,
∴选择半径为1的圆形纸片恰好和扇形丙组成(2)中的几何体,该几何体的表面积为π×12+=3π.
23.解:(1)如图,设点E是桥拱所在圆的圆心.
过点E作EF⊥AB于点F,延长EF交⊙E于点C,连结AE,
则CF=20米.由垂径定理知,F是AB的中点,
∴AF=FB=AB=40米.设桥拱所在圆的半径为r米,由勾股定理,
得AE2=AF2+EF2=AF2+(CE-CF)2,
即r2=402+(r-20)2,解得r=50.
∴桥拱所在圆的半径为50米.
(2)这艘轮船能顺利通过.理由如下:
如图,设MN=60米,MN∥AB,
EC与MN的交点为D,连结EM.
易知DE⊥MN,
∴MD=30米,
∴DE===40(米).
∵EF=EC-CF=50-20=30(米),
∴DF=DE-EF=40-30=10(米).
∵10米>9米,∴这艘轮船能顺利通过.
24.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°.∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB.
∵OD∥BC,∴∠DOE=∠ABC,
∴△DOE∽△ABC.
(2)证明:∵△DOE∽△ABC,
∴∠ODE=∠A.
∵∠A=∠BDC,∴∠ODE=∠BDC,
∴∠ODF=∠BDE.
(3)解:∵△DOE∽△ABC,
∴==,
即S△ABC=4S△DOE=4S1.
∵OA=OB,∴S△BOC=S△ABC,即S△BOC=2S1.
∵=,S2=S△BOC+S△DOE+S△DBE=2S1+S1+S△DBE,
∴S△DBE=S1,
∴BE=OE,即OE=OB=OD,
∴sin A=sin∠ODE==.
