七年级数学5.2.2 平行线的判定
文档属性
| 名称 | 七年级数学5.2.2 平行线的判定 | 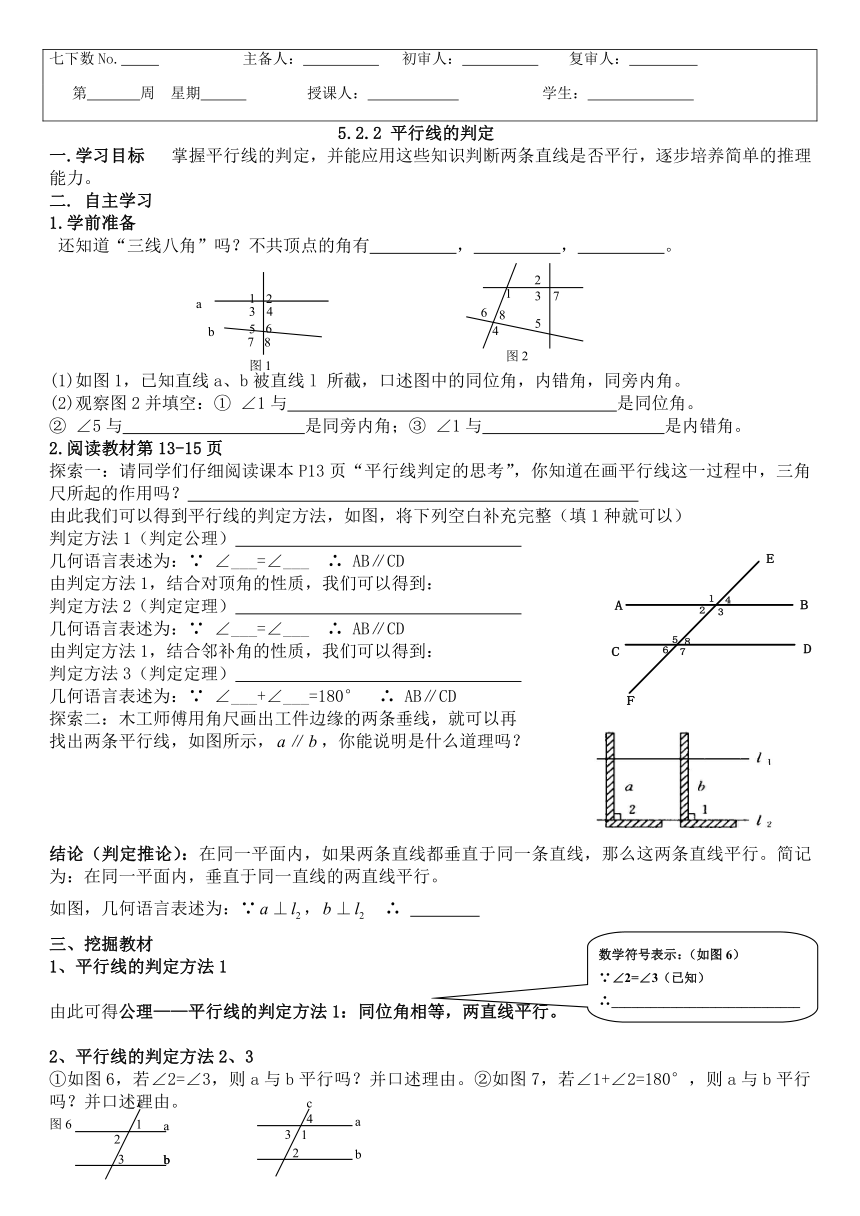 | |
| 格式 | zip | ||
| 文件大小 | 42.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-16 20:26:36 | ||
图片预览

文档简介
七下数No. 主备人: 初审人: 复审人:
第 周 星期 授课人: 学生:
5.2.2 平行线的判定
一.学习目标 掌握平行线的判定,并能应用这些知识判断两条直线是否平行,逐步培养简单的推理能力。
二. 自主学习
1.学前准备
还知道“三线八角”吗?不共顶点的角有 , , 。
(1)如图1,已知直线a、b被直线l 所截,口述图中的同位角,内错角,同旁内角。
(2)观察图2并填空:① ∠1与 是同位角。
② ∠5与 是同旁内角;③ ∠1与 是内错角。
2.阅读教材第13-15页
探索一:请同学们仔细阅读课本P13页“平行线判定的思考”,你知道在画平行线这一过程中,三角尺所起的作用吗?
由此我们可以得到平行线的判定方法,如图,将下列空白补充完整(填1种就可以)
判定方法1(判定公理)
几何语言表述为:∵ ∠___=∠___ ∴ AB∥CD
由判定方法1,结合对顶角的性质,我们可以得到:
判定方法2(判定定理)
几何语言表述为:∵ ∠___=∠___ ∴ AB∥CD
由判定方法1,结合邻补角的性质,我们可以得到:
判定方法3(判定定理)
几何语言表述为:∵ ∠___+∠___=180° ∴ AB∥CD
探索二:木工师傅用角尺画出工件边缘的两条垂线,就可以再
找出两条平行线,如图所示,∥,你能说明是什么道理吗?
结论(判定推论):在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。简记为:在同一平面内,垂直于同一直线的两直线平行。
如图,几何语言表述为:∵⊥,⊥ ∴
三、挖掘教材
1、平行线的判定方法1
由此可得公理——平行线的判定方法1:同位角相等,两直线平行。
2、平行线的判定方法2、3
①如图6,若∠2=∠3,则a与b平行吗?并口述理由。②如图7,若∠1+∠2=180°,则a与b平行吗?并口述理由。
图6
由此可以下得定理:
平行线的判定方法2:内错角相等,两直线平行。
平行线的判定方法3:同旁内角互补,两直线平行。
3、平行线的判定方法4:
如图10,(1)已知a⊥m,b⊥m,请判断直线
a与b间的位置关系;(2)用一句话总结出(1)中所包含的结论。
解:(1)直线a与b ,理由为:
∵a⊥m,b⊥m( )
∴∠1=∠2= ( )
∴b∥c( )
由此得到以下定理:
平行线的判定方法4:垂直于同一直线的两直线 。
思考:以上问题还有其它方法证明直线b∥c吗?试一试吧!
五、课堂检测
(一)、基础练习
1、在同一平面内,直线a、b相交于P,若a∥c,则b与c的位置关系是 。
2、不相邻的两个直角,如果它们有一边在同一直线上,那么另一边的位置关系是 。
3、如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C。
(1)由∠CBE=∠A可以判断___∥___,根据是_________________。
(2)由∠CBE=∠C可以判断___∥___,根据是_________________。
4、如图1所示,下列条件中,能判断AB∥CD的是( )毛
A.∠BAD=∠BCD B.∠1=∠2 C.∠3=∠4 D.∠BAC=∠ACD
(图1) (图2) (图3)
5、如图2所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
6、如图3所示,能判断AB∥CE的条件是( )
A.∠A=∠ACE B.∠A=∠ECD C.∠B=∠BCA D.∠B=∠ACE
7、如图,直线AB、CD被直线EF所截,∠1=∠2,直线AB和CD平行吗?为什么?
(二)、拓展探究
8、如图所示,已知直线a、b、c、d、e且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为 什么?
9、如图所示,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么,直线AB、CD的位置关系如何?
说明你的理由.
b
a
2
12111
3132111
43132111
543132111
6566643132111
76566643132111
876566643132111
图1
1
22
3
5
4
图2
6
7
8
数学符号表示:(如图6)
∵∠2=∠3(已知)
∴_____________________________
∴ a ∥b(内错角相等,两直线平行)
c
a
b
1
2
3
4
a
b
c
2
3
b
1
数学符号表示:(如图7)
∵_______________________(已知)
∴ a ∥b(同旁内角互补,两直线平行)
m
a
b
1
2
图10
数学符号表示:
∵a⊥m,b⊥m(已知)
∴ a ∥b(垂直于同一条直线的两直线平行)
第 周 星期 授课人: 学生:
5.2.2 平行线的判定
一.学习目标 掌握平行线的判定,并能应用这些知识判断两条直线是否平行,逐步培养简单的推理能力。
二. 自主学习
1.学前准备
还知道“三线八角”吗?不共顶点的角有 , , 。
(1)如图1,已知直线a、b被直线l 所截,口述图中的同位角,内错角,同旁内角。
(2)观察图2并填空:① ∠1与 是同位角。
② ∠5与 是同旁内角;③ ∠1与 是内错角。
2.阅读教材第13-15页
探索一:请同学们仔细阅读课本P13页“平行线判定的思考”,你知道在画平行线这一过程中,三角尺所起的作用吗?
由此我们可以得到平行线的判定方法,如图,将下列空白补充完整(填1种就可以)
判定方法1(判定公理)
几何语言表述为:∵ ∠___=∠___ ∴ AB∥CD
由判定方法1,结合对顶角的性质,我们可以得到:
判定方法2(判定定理)
几何语言表述为:∵ ∠___=∠___ ∴ AB∥CD
由判定方法1,结合邻补角的性质,我们可以得到:
判定方法3(判定定理)
几何语言表述为:∵ ∠___+∠___=180° ∴ AB∥CD
探索二:木工师傅用角尺画出工件边缘的两条垂线,就可以再
找出两条平行线,如图所示,∥,你能说明是什么道理吗?
结论(判定推论):在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。简记为:在同一平面内,垂直于同一直线的两直线平行。
如图,几何语言表述为:∵⊥,⊥ ∴
三、挖掘教材
1、平行线的判定方法1
由此可得公理——平行线的判定方法1:同位角相等,两直线平行。
2、平行线的判定方法2、3
①如图6,若∠2=∠3,则a与b平行吗?并口述理由。②如图7,若∠1+∠2=180°,则a与b平行吗?并口述理由。
图6
由此可以下得定理:
平行线的判定方法2:内错角相等,两直线平行。
平行线的判定方法3:同旁内角互补,两直线平行。
3、平行线的判定方法4:
如图10,(1)已知a⊥m,b⊥m,请判断直线
a与b间的位置关系;(2)用一句话总结出(1)中所包含的结论。
解:(1)直线a与b ,理由为:
∵a⊥m,b⊥m( )
∴∠1=∠2= ( )
∴b∥c( )
由此得到以下定理:
平行线的判定方法4:垂直于同一直线的两直线 。
思考:以上问题还有其它方法证明直线b∥c吗?试一试吧!
五、课堂检测
(一)、基础练习
1、在同一平面内,直线a、b相交于P,若a∥c,则b与c的位置关系是 。
2、不相邻的两个直角,如果它们有一边在同一直线上,那么另一边的位置关系是 。
3、如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C。
(1)由∠CBE=∠A可以判断___∥___,根据是_________________。
(2)由∠CBE=∠C可以判断___∥___,根据是_________________。
4、如图1所示,下列条件中,能判断AB∥CD的是( )毛
A.∠BAD=∠BCD B.∠1=∠2 C.∠3=∠4 D.∠BAC=∠ACD
(图1) (图2) (图3)
5、如图2所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
6、如图3所示,能判断AB∥CE的条件是( )
A.∠A=∠ACE B.∠A=∠ECD C.∠B=∠BCA D.∠B=∠ACE
7、如图,直线AB、CD被直线EF所截,∠1=∠2,直线AB和CD平行吗?为什么?
(二)、拓展探究
8、如图所示,已知直线a、b、c、d、e且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为 什么?
9、如图所示,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么,直线AB、CD的位置关系如何?
说明你的理由.
b
a
2
12111
3132111
43132111
543132111
6566643132111
76566643132111
876566643132111
图1
1
22
3
5
4
图2
6
7
8
数学符号表示:(如图6)
∵∠2=∠3(已知)
∴_____________________________
∴ a ∥b(内错角相等,两直线平行)
c
a
b
1
2
3
4
a
b
c
2
3
b
1
数学符号表示:(如图7)
∵_______________________(已知)
∴ a ∥b(同旁内角互补,两直线平行)
m
a
b
1
2
图10
数学符号表示:
∵a⊥m,b⊥m(已知)
∴ a ∥b(垂直于同一条直线的两直线平行)
