3.3.8正方形形的判定

(共17张PPT)
初中数学九年级上册
（苏科版）
1.3 正方形的判定
学习目标：
1.会证明正方形的判定定理.
2.能综合运用正方形的判定定理进行计算与证明.
教学重点：
正方形判定定理与平行四边形、矩形、正方形
判定定理的综合应用.
教学难点：
平行四边形、矩形、正方形判定定理的综合应用.
（一）知识梳理
1． 叫正方形．
2.由定义得正方形的判定方法：
的矩形叫正方形．
的菱形叫正方形．
既是 又是 的四边形叫正方形．
自主探究
有一组邻边相等,有一个角是直角且的平行四边形
有一组邻边相等
有一个角是直角
菱形
矩形
（一）知识梳理
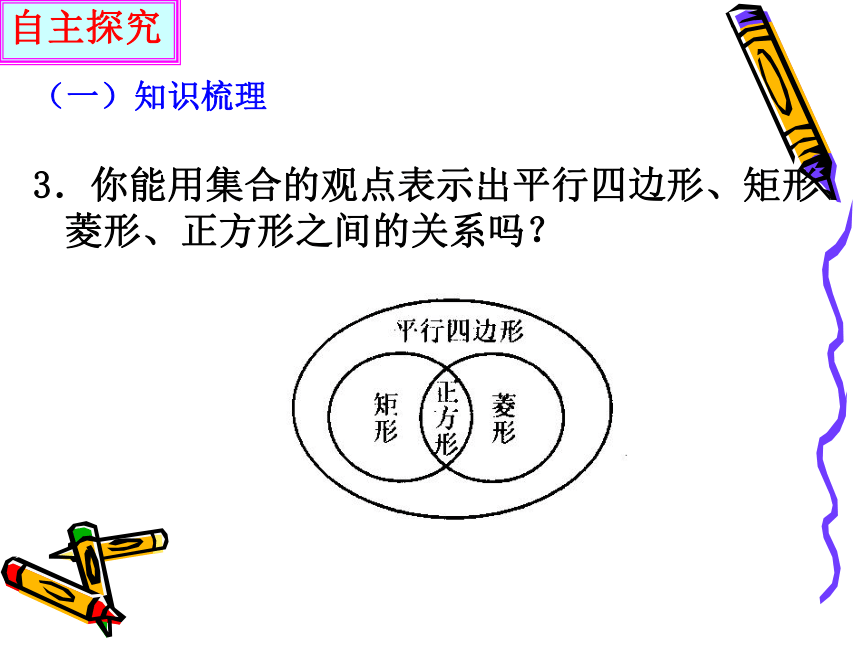
3．你能用集合的观点表示出平行四边形、矩形、菱形、正方形之间的关系吗？
自主探究
定义：
有一组邻边相等且有一个角是直角的平行四边形是正方形.
2. 正方形的判定方法
自主探究
定理：
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
3.如何证明正方形的判定定理？
（1）有一组邻边相等的矩形是正方形.
（2）有一个角是直角的菱形是正方形.
自主探究
动手实践
(1)用直尺和圆规作正方形；
(2)把长方形的纸片通过折纸，剪出一个正方
形纸片.说说你作图和剪纸的理由.
例1．
已知：如图，在Rt△ABC中，∠ACB=90°，CD
是∠ACB 的平分线，交AB于D，作
DE⊥AC，DF⊥BC，垂足为E、F．
求证：四边形DECF是正方形．
自主合作
证明：
∵ CD平分∠ACB， DE⊥BC， DF⊥AC，
∴ DE＝DF（角平分线上的点到角的两边距离相等）．
又∵ ∠DEC＝∠ECF＝∠CFD＝90°，
∴ 四边形CFDE是矩形（有三个角是直角的四边形是矩形），
又DE＝DF
∴ 四边形CFDE是正方形（有一组邻边相等的矩形是正方形）．
例2．
如图，以△ABC的边AB、AC为边的等边三角形ABD
和等边三角形ACE，四边形ADFE是平行四边形．
（1）当∠BAC满足＿＿＿＿时，四边形ADFE是矩形．
（2）当∠BAC满足＿＿＿＿时，平行四边形
ADFE不存在．
（3）当△ABC分别满足什么条件时，平行四
边形是菱形？是正方形？并说明理由．
自主合作
例3：
已知，如图，E、F、G、H分别是正方形ABCD各
边的中点，AF、BG、CH、DE分别两两相
交于点A′、B′、C′、D′ ．
求证：四边形A′B′C′D′是正方形 ．
自主合作
思考：
若例3的条件改为点E、F、G、H分别在正方形ABCD的各边上，且AE=BF=CG=DH，则四边形A′B′C′D′是正方形吗 证明你的结论.
自主合作
1．判断下列命题是否正确，并说明理由.
1.有一组邻边相等有一个角是直角的四边形是正方形;
2.有一个角是直角的菱形是正方形;
3.对角线相等的菱形是正方形;
4.对角线互相垂直的平行四边形是正方形;
5.对角线互相垂直平分且相等的四边形是正方形;
6.一组邻边相等且对角线互相平分且相等的四边形是正方形;
自主展示
X
X
使用正方形判定定理时要注意基础图形是四边形、平行四边形、矩形还是菱形.
X
自主展示
2．已知，四边形ABCD的对角线AC、BD相交于点O，则下列能判断它是正方形的条件的是：（ ）
（Ａ） AB=BC CD⊥DA
（Ｂ） AC=BC=CD=DA
（Ｃ） AO=CO，BO=DO，AC⊥BD
（Ｄ） AO=BO=CO=DO， AC⊥BD
D
3．证明：对角线互相垂直的矩形是正方形．
4．证明：对角线相等的菱形是正方形．
自主展示
如图①矩形ABCD的对角线AC、BD交于点O，过点D作DP∥OC，且DP＝OC，连结PC，
则四边形CODP是菱形．
(1)如果题目中的矩形变为菱形如图②,结论应变为什么？试说明．
(2)如果题目中的矩形变为正方形如图③，结论又应变为什么？ 并说明理由．
自主拓展
①
②
③
1.本节课你学到了哪些知识？
（正方形的判定定理）
2.本节课中你最大的收获是什么？
自主评价