3.4等腰梯形的性质和判定

(共15张PPT)
1.4 等腰梯形的性质和判定
学习目标：
1．掌握等腰梯形性质和判定的有关证明．
2．能够运用等腰梯形的性质和判定进行有
关问题的论证和计算，进一步培养学生
的分析能力和计算能力．
3．通过添加辅助线，把梯形的问题转化成
平行四边形或三角形问题，使学生体会
图形变换的方法和转化的思想．
教学重点：
解决梯形问题的基本方法（将梯形转化为平行四边形和三角形及正确运用辅助线）．
教学难点：
等腰梯形的性质和判定．
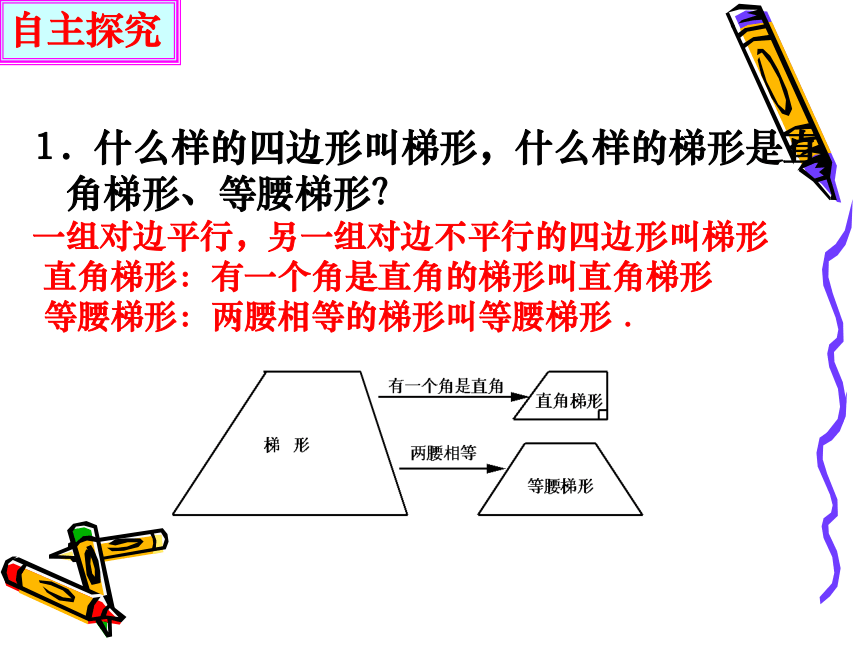
1．什么样的四边形叫梯形，什么样的梯形是直角梯形、等腰梯形？
一组对边平行，另一组对边不平行的四边形叫梯形
直角梯形：有一个角是直角的梯形叫直角梯形
等腰梯形：两腰相等的梯形叫等腰梯形 .
自主探究
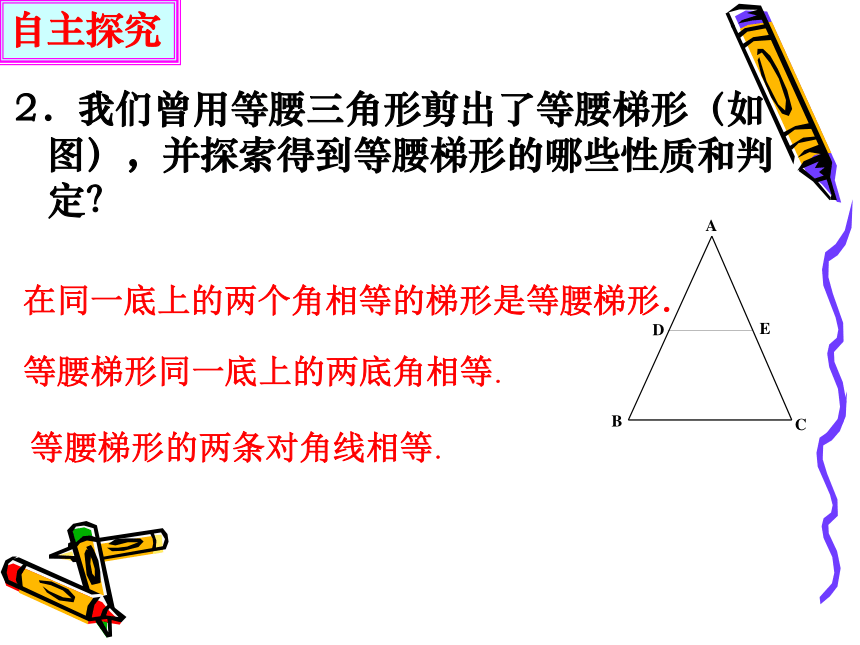
2．我们曾用等腰三角形剪出了等腰梯形（如图），并探索得到等腰梯形的哪些性质和判定？
自主探究
在同一底上的两个角相等的梯形是等腰梯形．
等腰梯形同一底上的两底角相等．
等腰梯形的两条对角线相等．
（一）等腰梯形的判定
1.定理：
在同一底上的两个角相等的梯形是等腰梯形．
自主合作
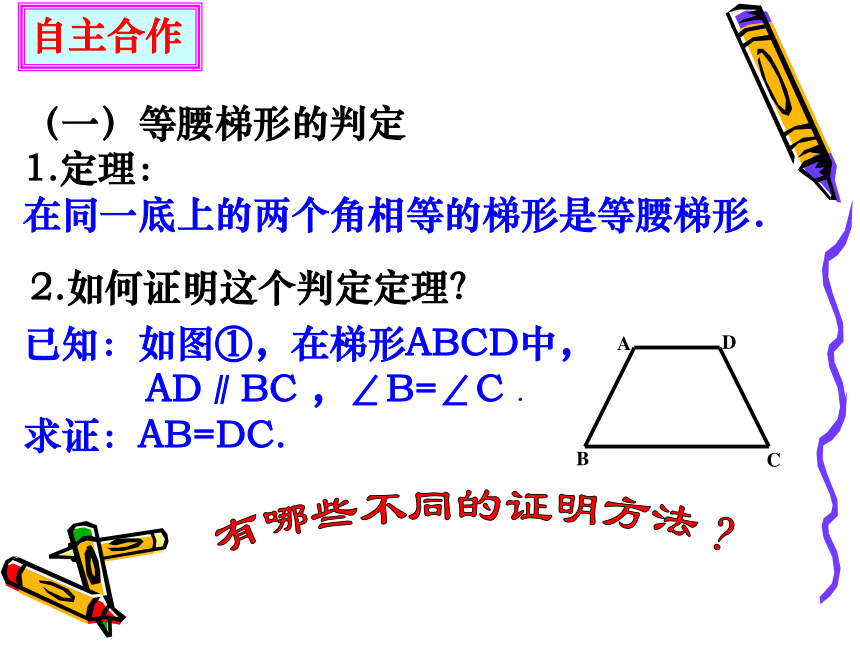
2.如何证明这个判定定理？
已知：如图①，在梯形ABCD中，
AD∥BC ，∠B=∠C ．
求证：AB=DC.
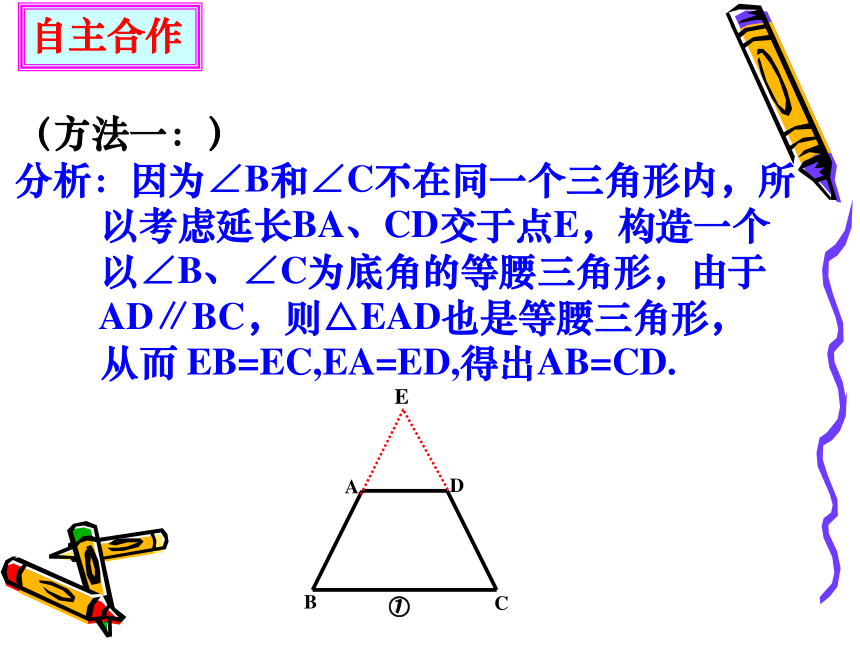
（方法一：）
分析：因为∠B和∠C不在同一个三角形内，所
以考虑延长BA、CD交于点E，构造一个
以∠B、∠C为底角的等腰三角形，由于
AD∥BC，则△EAD也是等腰三角形，
从而 EB=EC,EA=ED,得出AB=CD.
自主合作
E
①
（方法二：）
分析：如图②，过点D作DE∥AB，交BC
于E，得∠DEC=∠B=∠C，所以得
DE=DC .
自主合作
E
②
（方法三：）
分析：如图③作高AE、DF，通过证
Rt△ABE ≌ Rt△DFC推出AB=DC．
自主合作
③
E
F
（一）等腰梯形的性质
1.定理：
等腰梯形在同一底上的两个角相等．
等腰梯形的两条对角线相等．
自主合作
2.如何证明这两个性质定理？
已知：在梯形ABCD中，AD∥BC ，AB=DC.
求证： ∠B=∠C ．
求证：AC=BD．
解决梯形问题常用的方法 ：
自主拓展
（1）“平移一腰”，构造平行四边形和等腰三角形；
（2）“作高”：使两腰在两个直角三角形中
（3）“移对角线”：使两条对角线在同一个三角形中．
（4）“延腰”：构造具有公共角的两个等腰三角形．
（5）“等积变形”，连结梯形上底一端点和另一腰中点，并
延长与下底延长线交于一点，构成全等三角形．
E
E
F
E
1.本节课你学到了哪些知识？
2.本节课中你最大的收获是什么？
自主评价
1．证明：两条对角线相等的梯形是等腰梯形．
2．证明：等腰梯形一底的中点到另一底两端的
距离相等．
自主展示
3．若等腰梯形两底之差等于一腰的长，求腰
与两底夹角的度数．
如图，在等腰梯形ABCD中，AD∥BC，AB=CD=5，AD=6，BC=12．动点P从D点出发沿DC以每秒1个单位的速度向终点C运动，动点Q从点C出发沿CB以每秒2个单位的速度向点B运动，两点同时出发，当点P到达C点时，点Q随之停止运动．
（1）梯形ABCD的面积是 ；
（2）当PQ∥AB时，P点离开D点的时间等于 秒（3）当P、Q、C三点构成直角三角形时，P点离开
D点几秒？
自主拓展