2021-2022学年黑龙江省哈尔滨六十九中七年级(上)诊断数学试卷(10月份)(五四学制)(Word版 含解析)
文档属性
| 名称 | 2021-2022学年黑龙江省哈尔滨六十九中七年级(上)诊断数学试卷(10月份)(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 301.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 09:25:09 | ||
图片预览



文档简介
2021-2022学年黑龙江省哈尔滨六十九中七年级(上)诊断数学试卷(10月份)(五四学制)
一、选择题:(每题3分,共30分)
1.(3分)下列等式中是一元一次方程的是( )
A. B.x﹣y=0 C.3﹣2=1 D.x=0
2.(3分)下列各图中∠1和∠2为对顶角的是( )
A. B.
C. D.
3.(3分)下列方程中,解为x=2的方程是( )
A.4x=2 B.3x+6=0 C. D.7x﹣14=0
4.(3分)如图,∠AOC=135°,则∠BOC的度数为( )
A.55° B.45° C.35° D.25°
5.(3分)根据“x的3倍与5的和比x的多2”可列方程( )
A. B.
C. D.
6.(3分)将(3x+2)﹣2(2x﹣1)去括号正确的是( )
A.3x+2﹣2x+1 B.3x+2﹣4x+1 C.3x+2﹣4x﹣2 D.3x+2﹣4x+2
7.(3分)解方程1﹣,去分母,得( )
A.1﹣x﹣3=3x B.6﹣x﹣3=3x C.6﹣x+3=3x D.1﹣x+3=3x
8.(3分)如图,点A到线段BC的距离指的是下列哪条线段的长度( )
A.AB B.AC C.AD D.AE
9.(3分)下列等式变形正确的是( )
A.如果,那么
B.如果,那么x=3
C.如果mx=my,那么x=y
D.如果x﹣3=y﹣3,那么x﹣y=0
10.(3分)一商店把彩电按标价的九折出售,仍可获利20%,若该彩电的标价是3200元,则彩电的进价为多少元?设彩电的进价为x元/台,则可列方程为( )
A.3200×90%=20%x B.3200×90%=(1+20%)x
C.90%x=3200×20% D.90%x=3200×(1+20%)
二、填空题(每小题3分,共计30分)
11.(3分)一元一次方程3x+6=0的解是x= .
12.(3分)如图,口渴的马儿在A点处想尽快地到达小河边喝水,它应该沿着线路AB奔跑,其中的数学依据是 .
13.(3分)已知方程(m+1)x|m|+3=0是关于x的一元一次方程,则m的值是 .
14.(3分)若方程3x+6=12的解也是6x+3a=24的解,则a的值为 .
15.(3分)如图,若AB,AF被ED所截,则∠1与 是内错角.
16.(3分)一艘轮船在水中由A地开往B地,顺水航行用了4小时,由B地开往A地,逆水航行比顺水航行多用了1小时,已知此船在静水中速度是18千米/时,水流速度为 千米/小时.
17.(3分)七年级男生入住一楼,如果每间住6人,恰好空出一间;如果每间住5人就有4人没有房间住.那么一楼共有 间.
18.(3分)已知对于非零的两个实数a、b,规定a b=b﹣,若1 (x+1)=1,则x的值为 .
19.(3分)如图,直线AB与直线CD相交于点O,∠BOC:∠BOD=1:2,射线OE⊥CD,则∠BOE度数为 .
20.(3分)如图,点O在直线AB上,OC⊥OD于O,OE平分∠AOD,OF平分∠BOC,则∠EOF的度数为 .
三、解答题(21题6分,22题6分,23题5分,24题5分,25题6分,26题6分,27题6分,共计40分)
21.(6分)解方程:
(1)7x+6=8﹣3x;
(2).
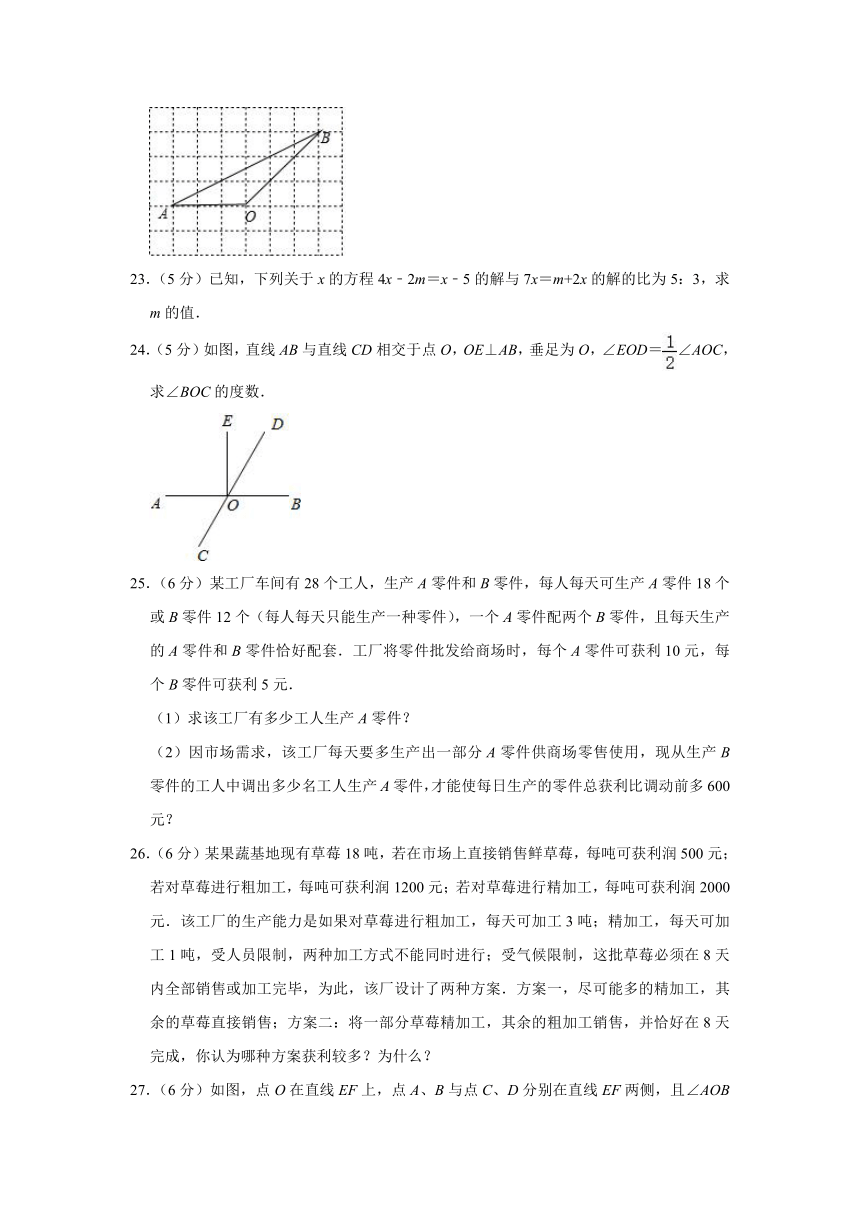
22.(6分)画图并回答:
在下图6×8的正方形网格中,每个小正方形的边长都为1个单位长度,△AOB的顶点A、B、O都在正方形网格的格点(两条虚线的交点)上.
(1)过点O画AB的垂线,交AB于点D;
(2)画点B到AO的垂线段BE;
(3)请直接写出三角形ABO的面积.
23.(5分)已知,下列关于x的方程4x﹣2m=x﹣5的解与7x=m+2x的解的比为5:3,求m的值.
24.(5分)如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=∠AOC,求∠BOC的度数.
25.(6分)某工厂车间有28个工人,生产A零件和B零件,每人每天可生产A零件18个或B零件12个(每人每天只能生产一种零件),一个A零件配两个B零件,且每天生产的A零件和B零件恰好配套.工厂将零件批发给商场时,每个A零件可获利10元,每个B零件可获利5元.
(1)求该工厂有多少工人生产A零件?
(2)因市场需求,该工厂每天要多生产出一部分A零件供商场零售使用,现从生产B零件的工人中调出多少名工人生产A零件,才能使每日生产的零件总获利比调动前多600元?
26.(6分)某果蔬基地现有草莓18吨,若在市场上直接销售鲜草莓,每吨可获利润500元;若对草莓进行粗加工,每吨可获利润1200元;若对草莓进行精加工,每吨可获利润2000元.该工厂的生产能力是如果对草莓进行粗加工,每天可加工3吨;精加工,每天可加工1吨,受人员限制,两种加工方式不能同时进行;受气候限制,这批草莓必须在8天内全部销售或加工完毕,为此,该厂设计了两种方案.方案一,尽可能多的精加工,其余的草莓直接销售;方案二:将一部分草莓精加工,其余的粗加工销售,并恰好在8天完成,你认为哪种方案获利较多?为什么?
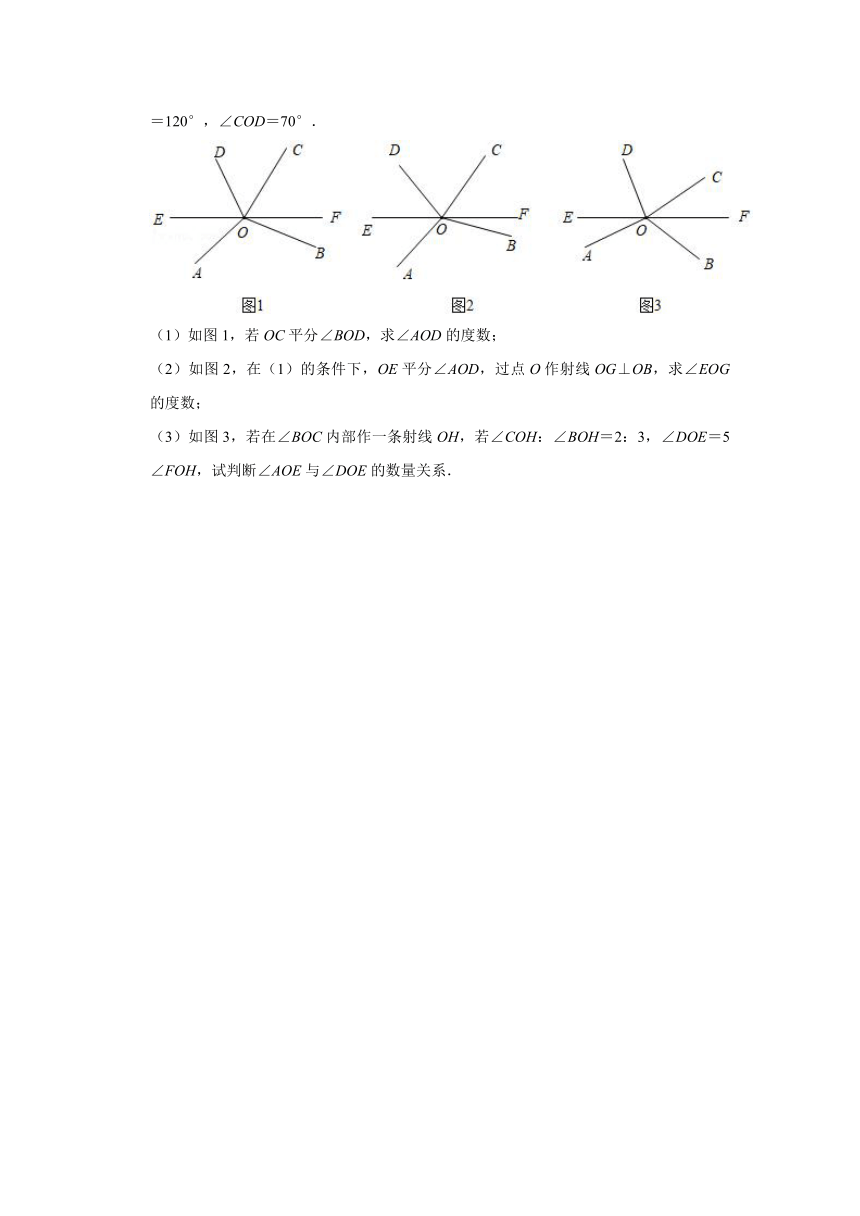
27.(6分)如图,点O在直线EF上,点A、B与点C、D分别在直线EF两侧,且∠AOB=120°,∠COD=70°.
(1)如图1,若OC平分∠BOD,求∠AOD的度数;
(2)如图2,在(1)的条件下,OE平分∠AOD,过点O作射线OG⊥OB,求∠EOG的度数;
(3)如图3,若在∠BOC内部作一条射线OH,若∠COH:∠BOH=2:3,∠DOE=5∠FOH,试判断∠AOE与∠DOE的数量关系.
2021-2022学年黑龙江省哈尔滨六十九中七年级(上)诊断数学试卷(10月份)(五四学制)
参考答案与试题解析
一、选择题:(每题3分,共30分)
1.(3分)下列等式中是一元一次方程的是( )
A. B.x﹣y=0 C.3﹣2=1 D.x=0
【分析】根据一元一次方程的定义逐项判断即可.
【解答】解:A.该方程是分式方程,故本选项不符合题意;
B.该方程中含有两个未知数,是二元一次方程,不是一元一次方程,故本选项不符合题意;
C.式子3﹣2=1中不含有未知数,不是方程,故本选项不符合题意;
D.x=0符合一元一次方程的定义,故本选项符合题意;
故选:D.
2.(3分)下列各图中∠1和∠2为对顶角的是( )
A. B.
C. D.
【分析】根据对顶角的两边互为反向延长线对各图形分析判断后进行解答.
【解答】解:根据对顶角的定义:
A中∠1和∠2不是对顶角;
B中∠1和∠2不是对顶角;
C中∠1和∠2是对顶角;
D中∠1和∠2不是对顶角;
故选:C.
3.(3分)下列方程中,解为x=2的方程是( )
A.4x=2 B.3x+6=0 C. D.7x﹣14=0
【分析】看看x=2能使ABCD四个选项中哪一个方程的左右两边相等,就是哪个答案;也可以分别解这四个选项中的方程.
【解答】解:(1)由4x=2得,x=;
(2)由3x+6=0得,x=﹣2;
(3)由x=0得,x=0;
(4)由7x﹣14=0得,x=2.
故选:D.
4.(3分)如图,∠AOC=135°,则∠BOC的度数为( )
A.55° B.45° C.35° D.25°
【分析】根据邻补角的定义是解决本题的关键.
【解答】解:由图得:∠AOC与∠BOC是邻补角.
∴∠AOC+∠BOC=180°,
∴∠BOC=180°﹣∠AOC=180°﹣135°=45°.
故选:B.
5.(3分)根据“x的3倍与5的和比x的多2”可列方程( )
A. B.
C. D.
【分析】根据题意可以列出相应的方程,本题得以解决.
【解答】解:由题意可得,
3x+5=x+2,
故选:B.
6.(3分)将(3x+2)﹣2(2x﹣1)去括号正确的是( )
A.3x+2﹣2x+1 B.3x+2﹣4x+1 C.3x+2﹣4x﹣2 D.3x+2﹣4x+2
【分析】根据去括号法则解答.
【解答】解:(3x+2)﹣2(2x﹣1)=3x+2﹣4x+2.
故选:D.
7.(3分)解方程1﹣,去分母,得( )
A.1﹣x﹣3=3x B.6﹣x﹣3=3x C.6﹣x+3=3x D.1﹣x+3=3x
【分析】去分母的方法是方程左右两边同时乘以分母的最小公倍数,注意分数线的括号的作用,并注意不能漏乘.
【解答】解:方程两边同时乘以6得6﹣x﹣3=3x.
故选:B.
8.(3分)如图,点A到线段BC的距离指的是下列哪条线段的长度( )
A.AB B.AC C.AD D.AE
【分析】直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
【解答】解:由图可得,AD⊥BC于D,点A到线段BC的距离指线段AD的长,
故选:C.
9.(3分)下列等式变形正确的是( )
A.如果,那么
B.如果,那么x=3
C.如果mx=my,那么x=y
D.如果x﹣3=y﹣3,那么x﹣y=0
【分析】根据等式的两边同时加上或减去同一个数或字母,等式仍成立;等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立,可得答案.
【解答】解:A、如果,那么b=,故A错误;
B、等式的左边乘以2,右边除以2,故B错误;
C、m=0时,错误;
D、等式的两边都加3后移项,故D正确;
故选:D.
10.(3分)一商店把彩电按标价的九折出售,仍可获利20%,若该彩电的标价是3200元,则彩电的进价为多少元?设彩电的进价为x元/台,则可列方程为( )
A.3200×90%=20%x B.3200×90%=(1+20%)x
C.90%x=3200×20% D.90%x=3200×(1+20%)
【分析】利用利润=售价﹣进价,即可得出关于x的一元一次方程,变形后即可得出结论.
【解答】解:依题意得:3200×90%﹣x=20%x,
即3200×90%=(1+20%)x.
故选:B.
二、填空题(每小题3分,共计30分)
11.(3分)一元一次方程3x+6=0的解是x= ﹣2 .
【分析】根据解方程的步骤:移项,合并同类项,系数化成1,即可求解.
【解答】解:3x+6=0,
3x=﹣6,
x=﹣2,
故答案为:﹣2.
12.(3分)如图,口渴的马儿在A点处想尽快地到达小河边喝水,它应该沿着线路AB奔跑,其中的数学依据是 垂线段最短 .
【分析】垂线段的性质:垂线段最短.据此判断即可.
【解答】解:口渴的马儿在A点处想尽快地到达小河边喝水,它应该沿着线路AB奔跑,其中的数学依据是垂线段最短.
故答案为:垂线段最短.
13.(3分)已知方程(m+1)x|m|+3=0是关于x的一元一次方程,则m的值是 1 .
【分析】若一个整式方程经过化简变形后,只含有一个未知数,并且未知数的次数都是1,系数不为0,则这个方程是一元一次方程.据此可根据未知数的系数及未知数的指数列出关于m的方程,继而求出m的值.
【解答】解:根据一元一次方程的特点可得,
解得m=1.
故填1.
14.(3分)若方程3x+6=12的解也是6x+3a=24的解,则a的值为 4 .
【分析】求出第一个方程的解得到x的值,代入第二个方程求出a的值即可.
【解答】解:方程3x+6=12,
解得:x=2,
把x=2代入得:12+3a=24,
解得:a=4,
故答案为:4
15.(3分)如图,若AB,AF被ED所截,则∠1与 ∠3 是内错角.
【分析】根据两个角分别在截线的两侧,且在两条直线之间,具有这样位置关系的一对角互为内错角进行分析解答即可.
【解答】解:若AB,AF被ED所截,则∠1与∠3是内错角,
故答案为:∠3.
16.(3分)一艘轮船在水中由A地开往B地,顺水航行用了4小时,由B地开往A地,逆水航行比顺水航行多用了1小时,已知此船在静水中速度是18千米/时,水流速度为 2 千米/小时.
【分析】设水流的速度为x千米/时,顺流的速度等于船在静水中的速度加上水流的速度,即(18+x)千米/时,逆流的速度等于船在静水中的速度减去水流的速度,即(18﹣x)千米/时,根据顺流航行的距离等于逆流航行的距离列方程求出x的值即可得出水流的速度.
【解答】解:设水流的速度为x千米/时,
根据题意得4(18+x)=5(18﹣x),
解得x=2,
所以水流的速度是2千米/时,
故答案为:2.
17.(3分)七年级男生入住一楼,如果每间住6人,恰好空出一间;如果每间住5人就有4人没有房间住.那么一楼共有 10 间.
【分析】设一楼共x间,则每间住6人,由于恰好空出一间,所以入住的总人数为6(x﹣1),若每间住5人,则同样的人数又可表示为5x+4,按这一相等关系列方程即可求出一楼的间数.
【解答】解:设一楼共x间,
根据题意得6(x﹣1)=5x+4,
解得x=10,
所以一楼共有10间,
故答案为:10.
18.(3分)已知对于非零的两个实数a、b,规定a b=b﹣,若1 (x+1)=1,则x的值为 2 .
【分析】根据新定义列出一元一次方程,解一元一次方程,即可求解.
【解答】解:∵a b=b﹣,
∴1 (x+1)=1,
(x+1)﹣=1,
x+1﹣2=1,
x﹣1=1,
x=2,
故答案为:2.
19.(3分)如图,直线AB与直线CD相交于点O,∠BOC:∠BOD=1:2,射线OE⊥CD,则∠BOE度数为 30°或130° .
【分析】】首先根据叙述作出图形,根据条件求得∠COB的度数,然后根据∠BOE=∠COE﹣∠COB即可求解.
【解答】解:
∵∠BOC=×180°=60°,
又∵OE⊥CD
∴∠COE=90°,
∴∠BOE=90°﹣60°=30°.
当点E′在EO的延长线上时,∠BOE′=∠COE′+∠BOC=90°+60°=150°
故答案是:30°或130°.
20.(3分)如图,点O在直线AB上,OC⊥OD于O,OE平分∠AOD,OF平分∠BOC,则∠EOF的度数为 45° .
【分析】由OC⊥OD于O,∠COD=90°,可求得∠EOF=180°﹣∠AOE﹣∠BOF,又由OE平分∠AOD,OF平分∠BOC,即可求得∠BOD与∠AOC的度数和,继而求得∠EOF的度数.
【解答】解:∵OC⊥OD于O,∠COD=90°,
∴∠EOF=180°﹣∠AOE﹣∠BOF,
∵OE平分∠AOD,OF平分∠BOC,
∴∠AOE=∠AOD,∠BOF=∠BOC,
∴∠EOF=180°﹣∠AOD﹣∠BOC
=180°﹣
=180
=
=
=
=45°.
故答案为:45°.
三、解答题(21题6分,22题6分,23题5分,24题5分,25题6分,26题6分,27题6分,共计40分)
21.(6分)解方程:
(1)7x+6=8﹣3x;
(2).
【分析】(1)根据解一元一次方程的步骤:移项、合并同类项、系数化成1,即可求解;
(2)根据解一元一次方程的步骤:去分母、去括号、移项、合并同类项、系数化成1,即可求解.
【解答】解:(1)7x+6=8﹣3x,
7x+3x=8﹣6,
10x=2,
;
(2),
5(2x+1)=15﹣3(x﹣1),
10x+5=15﹣3x+3,
10x+3x=18﹣5,
13x=13,
x=1.
22.(6分)画图并回答:
在下图6×8的正方形网格中,每个小正方形的边长都为1个单位长度,△AOB的顶点A、B、O都在正方形网格的格点(两条虚线的交点)上.
(1)过点O画AB的垂线,交AB于点D;
(2)画点B到AO的垂线段BE;
(3)请直接写出三角形ABO的面积.
【分析】(1)取格点T,连接OT交AB于点T,线段OD即为所求.
(2)利用网格的特征,数形结合的思想作出图形即可.
(3)利用三角形面积公式求解即可.
【解答】解:(1)如图,线段OD即为所求.
(2)如图,线段BE即为所求.
(3)S△AOB=×AO×BE=×3×3=.
23.(5分)已知,下列关于x的方程4x﹣2m=x﹣5的解与7x=m+2x的解的比为5:3,求m的值.
【分析】先解一元一次方程关于x的方程4x﹣2m=x﹣5的解与7x=m+2x,分别求得x,进而解决此题.
【解答】解:∵4x﹣2m=x﹣5,
∴4x﹣x=﹣5+2m.
∴3x=2m﹣5.
∴.
∵7x=m+2x,
∴7x﹣2x=m.
∴5x=m.
∴.
∴.
∴m=5.
经检验:当m=5时,3m≠0.
∴该方程的解为m=5.
24.(5分)如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=∠AOC,求∠BOC的度数.
【分析】利用垂直定义可得∠EOB=90°,然后根据∠EOD=∠AOC,设出未知数,列出方程,解出x的值,进而可得∠BOC的度数.
【解答】解:∵OE⊥AB,
∴∠EOB=90°,
∵∠EOD=∠AOC,
∴设∠AOC=x°,则∠EOD=x°,
∴∠BOD=x°,
∴x+x=90,
解得:x=60,
∴∠DOB=60°,
∴∠BOC=180°﹣60°=120°,
25.(6分)某工厂车间有28个工人,生产A零件和B零件,每人每天可生产A零件18个或B零件12个(每人每天只能生产一种零件),一个A零件配两个B零件,且每天生产的A零件和B零件恰好配套.工厂将零件批发给商场时,每个A零件可获利10元,每个B零件可获利5元.
(1)求该工厂有多少工人生产A零件?
(2)因市场需求,该工厂每天要多生产出一部分A零件供商场零售使用,现从生产B零件的工人中调出多少名工人生产A零件,才能使每日生产的零件总获利比调动前多600元?
【分析】(1)设该工厂有x名工人生产A零件,根据一个A零件配两个B零件可知,每天生产的两种零件恰好配套,则生产B零件的个数是A零件个数的2倍,根据这一相等关系列方程求出x的值即可;
(2)设从生产B零件的工人中调出y名工人生产A零件,则调整后生产A、B零件的人数、生产数量及获得利润可用含y的式子表示,原来7名工人生产A零件、21名工人生产B零件,获得的利润可以求出来,这两个利润的差是600元,根据这一数量关系列方程求出y的值即可.
【解答】解:(1)设该工厂有x名工人生产A零件,
根据题意得2×18x=12(28﹣x),
解得x=7,
答:该工厂有7名工人生产A零件.
(2)设从生产B零件的工人中调出y名工人生产A零件,
根据题意得10×18(7+y)+5×12(21﹣y)﹣(7×10×18+21×5×12)=600,
解得y=5,
答:从生产B零件的工人中调出5名工人生产A零件.
26.(6分)某果蔬基地现有草莓18吨,若在市场上直接销售鲜草莓,每吨可获利润500元;若对草莓进行粗加工,每吨可获利润1200元;若对草莓进行精加工,每吨可获利润2000元.该工厂的生产能力是如果对草莓进行粗加工,每天可加工3吨;精加工,每天可加工1吨,受人员限制,两种加工方式不能同时进行;受气候限制,这批草莓必须在8天内全部销售或加工完毕,为此,该厂设计了两种方案.方案一,尽可能多的精加工,其余的草莓直接销售;方案二:将一部分草莓精加工,其余的粗加工销售,并恰好在8天完成,你认为哪种方案获利较多?为什么?
【分析】先根据题意求出方案一的总获利,再设粗加工x天,则精加工(8﹣x)天,列出方程,求出方案二的总获利,然后进行比较,即可得出答案.
【解答】解:方案二获利较多.
理由:方案一:获利:8×1×2000+(18﹣8)×500=21000(元);
方案二:设x天精加工,则(8﹣x)天粗加工,
由题意得x+3(8﹣x)=18,
解得x=3,
8﹣x=5(天),
获利:3×2000+5×3×1200=24000(元),
∵24000>21000,
∴方案二获利较多.
27.(6分)如图,点O在直线EF上,点A、B与点C、D分别在直线EF两侧,且∠AOB=120°,∠COD=70°.
(1)如图1,若OC平分∠BOD,求∠AOD的度数;
(2)如图2,在(1)的条件下,OE平分∠AOD,过点O作射线OG⊥OB,求∠EOG的度数;
(3)如图3,若在∠BOC内部作一条射线OH,若∠COH:∠BOH=2:3,∠DOE=5∠FOH,试判断∠AOE与∠DOE的数量关系.
【分析】(1)根据角平分线定义和周角是360°可得∠AOC的度数;
(2)分两种情况:当OG在EF下方时;当OG在EF上方时,计算即可;
(3)由∠COH:∠BOH=2:3,∠DOE=5∠FOH,设∠DOE=5α,则∠FOH=α,再结合角平分线的性质可用α表达出∠COH∠BOC的度数,求出∠AOE与∠DOE的度数.
【解答】解:(1)∵OC平分∠BOD,
∴∠BOD=2∠COD=2×70°=140°,
∵∠AOB=120°,
∴∠AOD=360°﹣∠AOB﹣∠BOD=360°﹣120°﹣140°=100°.
(2)当OG在EF下方时,
∵OE平分∠AOD,∠AOD=100°,
∴,
∵OG⊥OB,
∴∠BOG=90°,
∴∠AOG=∠AOB﹣∠BOG=120°﹣90°=30°,
∴∠EOG=∠AOG+∠AOE=80°.
当OG在EF上方时,
∵OE平分∠AOD,∠AOD=100°,
∴,
∵OG⊥OB,
∴∠BOG=90°,
∵∠AOE+∠AOB+∠BOG+∠EOG=360°,∠AOB=120°,
∴∠EOG=360°﹣50°﹣120°﹣90°=100°;
(3)设∠DOE=5α,则∠FOH=α,
∴∠COH=180°﹣∠DOE﹣∠COD﹣∠FOH=110°﹣6α,
∴∠BOC=275°﹣15α,
∴∠AOD=360°﹣∠COD﹣∠BOC﹣∠AOB=360°﹣70°﹣(275°﹣15α)﹣120°=15α﹣105°,
∴∠AOE=10α﹣105°,
∴∠AOE=2∠DOE﹣105°.
一、选择题:(每题3分,共30分)
1.(3分)下列等式中是一元一次方程的是( )
A. B.x﹣y=0 C.3﹣2=1 D.x=0
2.(3分)下列各图中∠1和∠2为对顶角的是( )
A. B.
C. D.
3.(3分)下列方程中,解为x=2的方程是( )
A.4x=2 B.3x+6=0 C. D.7x﹣14=0
4.(3分)如图,∠AOC=135°,则∠BOC的度数为( )
A.55° B.45° C.35° D.25°
5.(3分)根据“x的3倍与5的和比x的多2”可列方程( )
A. B.
C. D.
6.(3分)将(3x+2)﹣2(2x﹣1)去括号正确的是( )
A.3x+2﹣2x+1 B.3x+2﹣4x+1 C.3x+2﹣4x﹣2 D.3x+2﹣4x+2
7.(3分)解方程1﹣,去分母,得( )
A.1﹣x﹣3=3x B.6﹣x﹣3=3x C.6﹣x+3=3x D.1﹣x+3=3x
8.(3分)如图,点A到线段BC的距离指的是下列哪条线段的长度( )
A.AB B.AC C.AD D.AE
9.(3分)下列等式变形正确的是( )
A.如果,那么
B.如果,那么x=3
C.如果mx=my,那么x=y
D.如果x﹣3=y﹣3,那么x﹣y=0
10.(3分)一商店把彩电按标价的九折出售,仍可获利20%,若该彩电的标价是3200元,则彩电的进价为多少元?设彩电的进价为x元/台,则可列方程为( )
A.3200×90%=20%x B.3200×90%=(1+20%)x
C.90%x=3200×20% D.90%x=3200×(1+20%)
二、填空题(每小题3分,共计30分)
11.(3分)一元一次方程3x+6=0的解是x= .
12.(3分)如图,口渴的马儿在A点处想尽快地到达小河边喝水,它应该沿着线路AB奔跑,其中的数学依据是 .
13.(3分)已知方程(m+1)x|m|+3=0是关于x的一元一次方程,则m的值是 .
14.(3分)若方程3x+6=12的解也是6x+3a=24的解,则a的值为 .
15.(3分)如图,若AB,AF被ED所截,则∠1与 是内错角.
16.(3分)一艘轮船在水中由A地开往B地,顺水航行用了4小时,由B地开往A地,逆水航行比顺水航行多用了1小时,已知此船在静水中速度是18千米/时,水流速度为 千米/小时.
17.(3分)七年级男生入住一楼,如果每间住6人,恰好空出一间;如果每间住5人就有4人没有房间住.那么一楼共有 间.
18.(3分)已知对于非零的两个实数a、b,规定a b=b﹣,若1 (x+1)=1,则x的值为 .
19.(3分)如图,直线AB与直线CD相交于点O,∠BOC:∠BOD=1:2,射线OE⊥CD,则∠BOE度数为 .
20.(3分)如图,点O在直线AB上,OC⊥OD于O,OE平分∠AOD,OF平分∠BOC,则∠EOF的度数为 .
三、解答题(21题6分,22题6分,23题5分,24题5分,25题6分,26题6分,27题6分,共计40分)
21.(6分)解方程:
(1)7x+6=8﹣3x;
(2).
22.(6分)画图并回答:
在下图6×8的正方形网格中,每个小正方形的边长都为1个单位长度,△AOB的顶点A、B、O都在正方形网格的格点(两条虚线的交点)上.
(1)过点O画AB的垂线,交AB于点D;
(2)画点B到AO的垂线段BE;
(3)请直接写出三角形ABO的面积.
23.(5分)已知,下列关于x的方程4x﹣2m=x﹣5的解与7x=m+2x的解的比为5:3,求m的值.
24.(5分)如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=∠AOC,求∠BOC的度数.
25.(6分)某工厂车间有28个工人,生产A零件和B零件,每人每天可生产A零件18个或B零件12个(每人每天只能生产一种零件),一个A零件配两个B零件,且每天生产的A零件和B零件恰好配套.工厂将零件批发给商场时,每个A零件可获利10元,每个B零件可获利5元.
(1)求该工厂有多少工人生产A零件?
(2)因市场需求,该工厂每天要多生产出一部分A零件供商场零售使用,现从生产B零件的工人中调出多少名工人生产A零件,才能使每日生产的零件总获利比调动前多600元?
26.(6分)某果蔬基地现有草莓18吨,若在市场上直接销售鲜草莓,每吨可获利润500元;若对草莓进行粗加工,每吨可获利润1200元;若对草莓进行精加工,每吨可获利润2000元.该工厂的生产能力是如果对草莓进行粗加工,每天可加工3吨;精加工,每天可加工1吨,受人员限制,两种加工方式不能同时进行;受气候限制,这批草莓必须在8天内全部销售或加工完毕,为此,该厂设计了两种方案.方案一,尽可能多的精加工,其余的草莓直接销售;方案二:将一部分草莓精加工,其余的粗加工销售,并恰好在8天完成,你认为哪种方案获利较多?为什么?
27.(6分)如图,点O在直线EF上,点A、B与点C、D分别在直线EF两侧,且∠AOB=120°,∠COD=70°.
(1)如图1,若OC平分∠BOD,求∠AOD的度数;
(2)如图2,在(1)的条件下,OE平分∠AOD,过点O作射线OG⊥OB,求∠EOG的度数;
(3)如图3,若在∠BOC内部作一条射线OH,若∠COH:∠BOH=2:3,∠DOE=5∠FOH,试判断∠AOE与∠DOE的数量关系.
2021-2022学年黑龙江省哈尔滨六十九中七年级(上)诊断数学试卷(10月份)(五四学制)
参考答案与试题解析
一、选择题:(每题3分,共30分)
1.(3分)下列等式中是一元一次方程的是( )
A. B.x﹣y=0 C.3﹣2=1 D.x=0
【分析】根据一元一次方程的定义逐项判断即可.
【解答】解:A.该方程是分式方程,故本选项不符合题意;
B.该方程中含有两个未知数,是二元一次方程,不是一元一次方程,故本选项不符合题意;
C.式子3﹣2=1中不含有未知数,不是方程,故本选项不符合题意;
D.x=0符合一元一次方程的定义,故本选项符合题意;
故选:D.
2.(3分)下列各图中∠1和∠2为对顶角的是( )
A. B.
C. D.
【分析】根据对顶角的两边互为反向延长线对各图形分析判断后进行解答.
【解答】解:根据对顶角的定义:
A中∠1和∠2不是对顶角;
B中∠1和∠2不是对顶角;
C中∠1和∠2是对顶角;
D中∠1和∠2不是对顶角;
故选:C.
3.(3分)下列方程中,解为x=2的方程是( )
A.4x=2 B.3x+6=0 C. D.7x﹣14=0
【分析】看看x=2能使ABCD四个选项中哪一个方程的左右两边相等,就是哪个答案;也可以分别解这四个选项中的方程.
【解答】解:(1)由4x=2得,x=;
(2)由3x+6=0得,x=﹣2;
(3)由x=0得,x=0;
(4)由7x﹣14=0得,x=2.
故选:D.
4.(3分)如图,∠AOC=135°,则∠BOC的度数为( )
A.55° B.45° C.35° D.25°
【分析】根据邻补角的定义是解决本题的关键.
【解答】解:由图得:∠AOC与∠BOC是邻补角.
∴∠AOC+∠BOC=180°,
∴∠BOC=180°﹣∠AOC=180°﹣135°=45°.
故选:B.
5.(3分)根据“x的3倍与5的和比x的多2”可列方程( )
A. B.
C. D.
【分析】根据题意可以列出相应的方程,本题得以解决.
【解答】解:由题意可得,
3x+5=x+2,
故选:B.
6.(3分)将(3x+2)﹣2(2x﹣1)去括号正确的是( )
A.3x+2﹣2x+1 B.3x+2﹣4x+1 C.3x+2﹣4x﹣2 D.3x+2﹣4x+2
【分析】根据去括号法则解答.
【解答】解:(3x+2)﹣2(2x﹣1)=3x+2﹣4x+2.
故选:D.
7.(3分)解方程1﹣,去分母,得( )
A.1﹣x﹣3=3x B.6﹣x﹣3=3x C.6﹣x+3=3x D.1﹣x+3=3x
【分析】去分母的方法是方程左右两边同时乘以分母的最小公倍数,注意分数线的括号的作用,并注意不能漏乘.
【解答】解:方程两边同时乘以6得6﹣x﹣3=3x.
故选:B.
8.(3分)如图,点A到线段BC的距离指的是下列哪条线段的长度( )
A.AB B.AC C.AD D.AE
【分析】直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
【解答】解:由图可得,AD⊥BC于D,点A到线段BC的距离指线段AD的长,
故选:C.
9.(3分)下列等式变形正确的是( )
A.如果,那么
B.如果,那么x=3
C.如果mx=my,那么x=y
D.如果x﹣3=y﹣3,那么x﹣y=0
【分析】根据等式的两边同时加上或减去同一个数或字母,等式仍成立;等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立,可得答案.
【解答】解:A、如果,那么b=,故A错误;
B、等式的左边乘以2,右边除以2,故B错误;
C、m=0时,错误;
D、等式的两边都加3后移项,故D正确;
故选:D.
10.(3分)一商店把彩电按标价的九折出售,仍可获利20%,若该彩电的标价是3200元,则彩电的进价为多少元?设彩电的进价为x元/台,则可列方程为( )
A.3200×90%=20%x B.3200×90%=(1+20%)x
C.90%x=3200×20% D.90%x=3200×(1+20%)
【分析】利用利润=售价﹣进价,即可得出关于x的一元一次方程,变形后即可得出结论.
【解答】解:依题意得:3200×90%﹣x=20%x,
即3200×90%=(1+20%)x.
故选:B.
二、填空题(每小题3分,共计30分)
11.(3分)一元一次方程3x+6=0的解是x= ﹣2 .
【分析】根据解方程的步骤:移项,合并同类项,系数化成1,即可求解.
【解答】解:3x+6=0,
3x=﹣6,
x=﹣2,
故答案为:﹣2.
12.(3分)如图,口渴的马儿在A点处想尽快地到达小河边喝水,它应该沿着线路AB奔跑,其中的数学依据是 垂线段最短 .
【分析】垂线段的性质:垂线段最短.据此判断即可.
【解答】解:口渴的马儿在A点处想尽快地到达小河边喝水,它应该沿着线路AB奔跑,其中的数学依据是垂线段最短.
故答案为:垂线段最短.
13.(3分)已知方程(m+1)x|m|+3=0是关于x的一元一次方程,则m的值是 1 .
【分析】若一个整式方程经过化简变形后,只含有一个未知数,并且未知数的次数都是1,系数不为0,则这个方程是一元一次方程.据此可根据未知数的系数及未知数的指数列出关于m的方程,继而求出m的值.
【解答】解:根据一元一次方程的特点可得,
解得m=1.
故填1.
14.(3分)若方程3x+6=12的解也是6x+3a=24的解,则a的值为 4 .
【分析】求出第一个方程的解得到x的值,代入第二个方程求出a的值即可.
【解答】解:方程3x+6=12,
解得:x=2,
把x=2代入得:12+3a=24,
解得:a=4,
故答案为:4
15.(3分)如图,若AB,AF被ED所截,则∠1与 ∠3 是内错角.
【分析】根据两个角分别在截线的两侧,且在两条直线之间,具有这样位置关系的一对角互为内错角进行分析解答即可.
【解答】解:若AB,AF被ED所截,则∠1与∠3是内错角,
故答案为:∠3.
16.(3分)一艘轮船在水中由A地开往B地,顺水航行用了4小时,由B地开往A地,逆水航行比顺水航行多用了1小时,已知此船在静水中速度是18千米/时,水流速度为 2 千米/小时.
【分析】设水流的速度为x千米/时,顺流的速度等于船在静水中的速度加上水流的速度,即(18+x)千米/时,逆流的速度等于船在静水中的速度减去水流的速度,即(18﹣x)千米/时,根据顺流航行的距离等于逆流航行的距离列方程求出x的值即可得出水流的速度.
【解答】解:设水流的速度为x千米/时,
根据题意得4(18+x)=5(18﹣x),
解得x=2,
所以水流的速度是2千米/时,
故答案为:2.
17.(3分)七年级男生入住一楼,如果每间住6人,恰好空出一间;如果每间住5人就有4人没有房间住.那么一楼共有 10 间.
【分析】设一楼共x间,则每间住6人,由于恰好空出一间,所以入住的总人数为6(x﹣1),若每间住5人,则同样的人数又可表示为5x+4,按这一相等关系列方程即可求出一楼的间数.
【解答】解:设一楼共x间,
根据题意得6(x﹣1)=5x+4,
解得x=10,
所以一楼共有10间,
故答案为:10.
18.(3分)已知对于非零的两个实数a、b,规定a b=b﹣,若1 (x+1)=1,则x的值为 2 .
【分析】根据新定义列出一元一次方程,解一元一次方程,即可求解.
【解答】解:∵a b=b﹣,
∴1 (x+1)=1,
(x+1)﹣=1,
x+1﹣2=1,
x﹣1=1,
x=2,
故答案为:2.
19.(3分)如图,直线AB与直线CD相交于点O,∠BOC:∠BOD=1:2,射线OE⊥CD,则∠BOE度数为 30°或130° .
【分析】】首先根据叙述作出图形,根据条件求得∠COB的度数,然后根据∠BOE=∠COE﹣∠COB即可求解.
【解答】解:
∵∠BOC=×180°=60°,
又∵OE⊥CD
∴∠COE=90°,
∴∠BOE=90°﹣60°=30°.
当点E′在EO的延长线上时,∠BOE′=∠COE′+∠BOC=90°+60°=150°
故答案是:30°或130°.
20.(3分)如图,点O在直线AB上,OC⊥OD于O,OE平分∠AOD,OF平分∠BOC,则∠EOF的度数为 45° .
【分析】由OC⊥OD于O,∠COD=90°,可求得∠EOF=180°﹣∠AOE﹣∠BOF,又由OE平分∠AOD,OF平分∠BOC,即可求得∠BOD与∠AOC的度数和,继而求得∠EOF的度数.
【解答】解:∵OC⊥OD于O,∠COD=90°,
∴∠EOF=180°﹣∠AOE﹣∠BOF,
∵OE平分∠AOD,OF平分∠BOC,
∴∠AOE=∠AOD,∠BOF=∠BOC,
∴∠EOF=180°﹣∠AOD﹣∠BOC
=180°﹣
=180
=
=
=
=45°.
故答案为:45°.
三、解答题(21题6分,22题6分,23题5分,24题5分,25题6分,26题6分,27题6分,共计40分)
21.(6分)解方程:
(1)7x+6=8﹣3x;
(2).
【分析】(1)根据解一元一次方程的步骤:移项、合并同类项、系数化成1,即可求解;
(2)根据解一元一次方程的步骤:去分母、去括号、移项、合并同类项、系数化成1,即可求解.
【解答】解:(1)7x+6=8﹣3x,
7x+3x=8﹣6,
10x=2,
;
(2),
5(2x+1)=15﹣3(x﹣1),
10x+5=15﹣3x+3,
10x+3x=18﹣5,
13x=13,
x=1.
22.(6分)画图并回答:
在下图6×8的正方形网格中,每个小正方形的边长都为1个单位长度,△AOB的顶点A、B、O都在正方形网格的格点(两条虚线的交点)上.
(1)过点O画AB的垂线,交AB于点D;
(2)画点B到AO的垂线段BE;
(3)请直接写出三角形ABO的面积.
【分析】(1)取格点T,连接OT交AB于点T,线段OD即为所求.
(2)利用网格的特征,数形结合的思想作出图形即可.
(3)利用三角形面积公式求解即可.
【解答】解:(1)如图,线段OD即为所求.
(2)如图,线段BE即为所求.
(3)S△AOB=×AO×BE=×3×3=.
23.(5分)已知,下列关于x的方程4x﹣2m=x﹣5的解与7x=m+2x的解的比为5:3,求m的值.
【分析】先解一元一次方程关于x的方程4x﹣2m=x﹣5的解与7x=m+2x,分别求得x,进而解决此题.
【解答】解:∵4x﹣2m=x﹣5,
∴4x﹣x=﹣5+2m.
∴3x=2m﹣5.
∴.
∵7x=m+2x,
∴7x﹣2x=m.
∴5x=m.
∴.
∴.
∴m=5.
经检验:当m=5时,3m≠0.
∴该方程的解为m=5.
24.(5分)如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=∠AOC,求∠BOC的度数.
【分析】利用垂直定义可得∠EOB=90°,然后根据∠EOD=∠AOC,设出未知数,列出方程,解出x的值,进而可得∠BOC的度数.
【解答】解:∵OE⊥AB,
∴∠EOB=90°,
∵∠EOD=∠AOC,
∴设∠AOC=x°,则∠EOD=x°,
∴∠BOD=x°,
∴x+x=90,
解得:x=60,
∴∠DOB=60°,
∴∠BOC=180°﹣60°=120°,
25.(6分)某工厂车间有28个工人,生产A零件和B零件,每人每天可生产A零件18个或B零件12个(每人每天只能生产一种零件),一个A零件配两个B零件,且每天生产的A零件和B零件恰好配套.工厂将零件批发给商场时,每个A零件可获利10元,每个B零件可获利5元.
(1)求该工厂有多少工人生产A零件?
(2)因市场需求,该工厂每天要多生产出一部分A零件供商场零售使用,现从生产B零件的工人中调出多少名工人生产A零件,才能使每日生产的零件总获利比调动前多600元?
【分析】(1)设该工厂有x名工人生产A零件,根据一个A零件配两个B零件可知,每天生产的两种零件恰好配套,则生产B零件的个数是A零件个数的2倍,根据这一相等关系列方程求出x的值即可;
(2)设从生产B零件的工人中调出y名工人生产A零件,则调整后生产A、B零件的人数、生产数量及获得利润可用含y的式子表示,原来7名工人生产A零件、21名工人生产B零件,获得的利润可以求出来,这两个利润的差是600元,根据这一数量关系列方程求出y的值即可.
【解答】解:(1)设该工厂有x名工人生产A零件,
根据题意得2×18x=12(28﹣x),
解得x=7,
答:该工厂有7名工人生产A零件.
(2)设从生产B零件的工人中调出y名工人生产A零件,
根据题意得10×18(7+y)+5×12(21﹣y)﹣(7×10×18+21×5×12)=600,
解得y=5,
答:从生产B零件的工人中调出5名工人生产A零件.
26.(6分)某果蔬基地现有草莓18吨,若在市场上直接销售鲜草莓,每吨可获利润500元;若对草莓进行粗加工,每吨可获利润1200元;若对草莓进行精加工,每吨可获利润2000元.该工厂的生产能力是如果对草莓进行粗加工,每天可加工3吨;精加工,每天可加工1吨,受人员限制,两种加工方式不能同时进行;受气候限制,这批草莓必须在8天内全部销售或加工完毕,为此,该厂设计了两种方案.方案一,尽可能多的精加工,其余的草莓直接销售;方案二:将一部分草莓精加工,其余的粗加工销售,并恰好在8天完成,你认为哪种方案获利较多?为什么?
【分析】先根据题意求出方案一的总获利,再设粗加工x天,则精加工(8﹣x)天,列出方程,求出方案二的总获利,然后进行比较,即可得出答案.
【解答】解:方案二获利较多.
理由:方案一:获利:8×1×2000+(18﹣8)×500=21000(元);
方案二:设x天精加工,则(8﹣x)天粗加工,
由题意得x+3(8﹣x)=18,
解得x=3,
8﹣x=5(天),
获利:3×2000+5×3×1200=24000(元),
∵24000>21000,
∴方案二获利较多.
27.(6分)如图,点O在直线EF上,点A、B与点C、D分别在直线EF两侧,且∠AOB=120°,∠COD=70°.
(1)如图1,若OC平分∠BOD,求∠AOD的度数;
(2)如图2,在(1)的条件下,OE平分∠AOD,过点O作射线OG⊥OB,求∠EOG的度数;
(3)如图3,若在∠BOC内部作一条射线OH,若∠COH:∠BOH=2:3,∠DOE=5∠FOH,试判断∠AOE与∠DOE的数量关系.
【分析】(1)根据角平分线定义和周角是360°可得∠AOC的度数;
(2)分两种情况:当OG在EF下方时;当OG在EF上方时,计算即可;
(3)由∠COH:∠BOH=2:3,∠DOE=5∠FOH,设∠DOE=5α,则∠FOH=α,再结合角平分线的性质可用α表达出∠COH∠BOC的度数,求出∠AOE与∠DOE的度数.
【解答】解:(1)∵OC平分∠BOD,
∴∠BOD=2∠COD=2×70°=140°,
∵∠AOB=120°,
∴∠AOD=360°﹣∠AOB﹣∠BOD=360°﹣120°﹣140°=100°.
(2)当OG在EF下方时,
∵OE平分∠AOD,∠AOD=100°,
∴,
∵OG⊥OB,
∴∠BOG=90°,
∴∠AOG=∠AOB﹣∠BOG=120°﹣90°=30°,
∴∠EOG=∠AOG+∠AOE=80°.
当OG在EF上方时,
∵OE平分∠AOD,∠AOD=100°,
∴,
∵OG⊥OB,
∴∠BOG=90°,
∵∠AOE+∠AOB+∠BOG+∠EOG=360°,∠AOB=120°,
∴∠EOG=360°﹣50°﹣120°﹣90°=100°;
(3)设∠DOE=5α,则∠FOH=α,
∴∠COH=180°﹣∠DOE﹣∠COD﹣∠FOH=110°﹣6α,
∴∠BOC=275°﹣15α,
∴∠AOD=360°﹣∠COD﹣∠BOC﹣∠AOB=360°﹣70°﹣(275°﹣15α)﹣120°=15α﹣105°,
∴∠AOE=10α﹣105°,
∴∠AOE=2∠DOE﹣105°.
同课章节目录
