2021-2022学年度北师版八年级数学下册教案 3.1图形的平移
文档属性
| 名称 | 2021-2022学年度北师版八年级数学下册教案 3.1图形的平移 |  | |
| 格式 | DOC | ||
| 文件大小 | 349.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 08:16:49 | ||
图片预览




文档简介
1 图形的平移
第1课时 平移的认识
教学目标
一、基本目标
1.认识平移,说出平移的定义,理解平移的基本内涵.
2.经历观察、分析、操作、欣赏以及抽象、概括等过程,探索图形平移的基本性质.
3.通过探究,归纳平移的定义、特征、性质,积累数学活动经验,进一步发展空间观念,增强空间想象力.
二、重难点目标
【教学重点】
理解并掌握平移的定义及性质.
【教学难点】
根据平移的性质进行简单的平移作图.
教学过程
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P65~P67的内容,完成下面练习.
【3 min反馈】
1.在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.平移不改变图形的形状和大小.
2. 一个图形和它经过平移所得的图形中,对应点所连的线段平行(或在一条直线上)且相等,对应线段平行(或在一条直线上)且相等,对应角相等.
3.下列运动属于平移的是( A )
A.急刹车时汽车在地面上的滑动
B.冷水加热中,小气泡上升为大气泡
C.随风飘动的风筝在空中的运动
D.随手抛出的彩球的运动
4.如图所示,下列每组图形中的两个三角形不是通过平移得到的是( B )
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
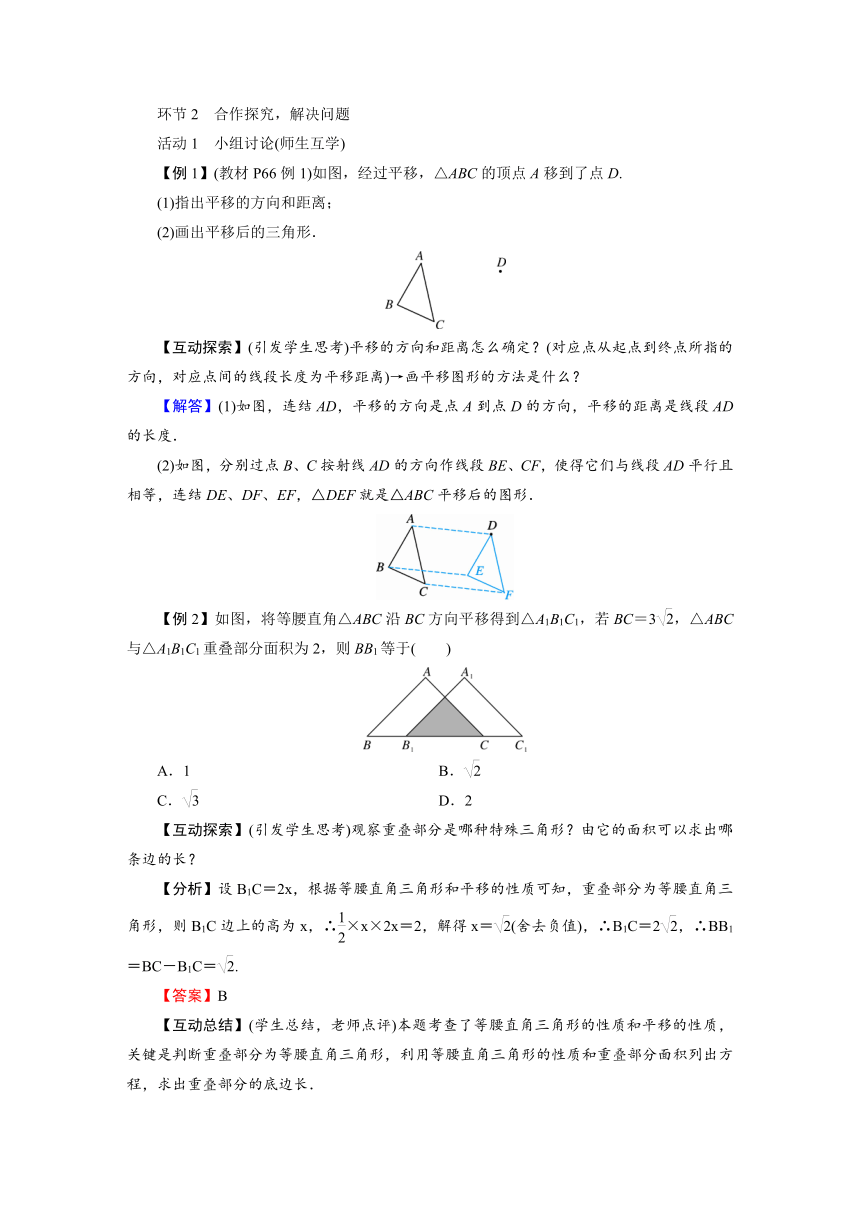
【例1】(教材P66例1)如图,经过平移,△ABC的顶点A移到了点D.
(1)指出平移的方向和距离;
(2)画出平移后的三角形.
【互动探索】(引发学生思考)平移的方向和距离怎么确定?(对应点从起点到终点所指的方向,对应点间的线段长度为平移距离)→画平移图形的方法是什么?
【解答】(1)如图,连结AD,平移的方向是点A到点D的方向,平移的距离是线段AD的长度.
(2)如图,分别过点B、C按射线AD的方向作线段BE、CF,使得它们与线段AD平行且相等,连结DE、DF、EF,△DEF就是△ABC平移后的图形.
【例2】如图,将等腰直角△ABC沿BC方向平移得到△A1B1C1,若BC=3,△ABC与△A1B1C1重叠部分面积为2,则BB1等于( )
A.1 B.
C. D.2
【互动探索】(引发学生思考)观察重叠部分是哪种特殊三角形?由它的面积可以求出哪条边的长?
【分析】设B1C=2x,根据等腰直角三角形和平移的性质可知,重叠部分为等腰直角三角形,则B1C边上的高为x,∴×x×2x=2,解得x=(舍去负值),∴B1C=2,∴BB1=BC-B1C=.
【答案】B
【互动总结】(学生总结,老师点评)本题考查了等腰直角三角形的性质和平移的性质,关键是判断重叠部分为等腰直角三角形,利用等腰直角三角形的性质和重叠部分面积列出方程,求出重叠部分的底边长.
活动2 巩固练习(学生独学)
1.下列说法正确的是( B )
A.两个全等的图形可看作其中一个是由另一个平移得到的
B.由平移得到的两个图形对应点连线互相平行(或共线)
C.由平移得到的两个等腰三角形周长一定相等,但面积未必相等
D.边长相等的两个正方形一定可以通过平移得到
2.下列现象:①电风扇的转动;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上瓶装饮料的移动.其中属于平移的是②④.(填序号)
3.如图所示,一张白色正方形纸片的边长是10 cm,被两张宽为2 cm的纸条(阴影部分)分为四个白色的长方形部分,请你利用平移的知识求出图中白色部分的面积.
解:把图中的阴影部分平移到正方形纸片相邻的两边上,这时图中的四个白色长方形变成了一个正方形,且边长为10-2=8(cm),则面积为82=64(cm2),故图中白色部分的面积为64 cm2.
活动3 拓展延伸(学生对学)
【例3】如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移线段BE的距离,就得到此图形,下列结论正确的有( )
①AC∥DF;②HE=5;③CF=5;④阴影部分面积为.
A.1个 B.2个
C.3个 D.4个
【互动探索】根据平移的性质得出对应点所连的线段平行且相等,对应角相等,对应线段平行且相等,阴影部分和三角形面积之间的关系,结合图形与所给的结论即可得出答案.
【分析】①由对应线段平行可得AC∥DF,正确;②由对应线段相等可得AB=DE=8,则HE=DE-DH=8-3=5,正确;③平移的距离CF=BE=5,正确;④S四边形HDFC=S梯形ABEH=(AB+EH)·BE=×(8+5)×5=,错误.
【答案】C
【互动总结】(学生总结,老师点评)本题考查平移的基本性质:(1)平移不改变图形的形状和大小;(2)对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
1.平移的定义
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
2.平移的性质
一个图形和它经过平移所得的图形中,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等,对应角相等.
3.简单的平移作图
练习设计
请完成本课时对应练习!
第2课时 坐标系中的点沿x轴、y轴的一次平移
教学目标
一、基本目标
1.进一步理解平移的意义和平移的性质.
2.通过“变化的鱼”探究横向(或纵向)平移一次,其坐标变化的规律,认识图形变换与坐标之间的内在联系.
3.理解并掌握图形平移在平面直角坐标系中的坐标变化规律,即:向右平移几,就是横坐标加几;向左平移几,就是横坐标减几;向上平移几,就是纵坐标加几;向下平移几,就是纵坐标减几.
二、重难点目标
【教学重点】
理解和掌握直角坐标系中图形的坐标变化规律.
【教学难点】
对图形平移在平面直角坐标系中的坐标变化规律的探究.
教学过程
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P68~P69的内容,完成下面练习.
【3 min反馈】
1.在平面直角坐标系中,如果把图形中点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原来的图形沿着x轴向右(或向左)平移a个单位长度.
2.在平面直角坐标系中,如果把图形中点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原来的图形沿着y轴向上(或向下)平移a个单位长度.
3.如果一个图案沿x轴负方向平移3个单位长度,那么这个图案上的点的坐标变化为( B )
A.横坐标不变,纵坐标减少3个单位长度
B.纵坐标不变,横坐标减少3个单位长度
C.横、纵坐标都没有变化
D.横、纵坐标都减少3个单位长度
4.点M(-2,5)是由点N向上平移3个单位长度得到的,则点N的坐标为( A )
A.(-2,2) B.(-5,5)
C.(-2,8) D.(1,5)
5.如图所示,经过平移,小船上的点A移到了点B,作出平移后的小船.
解:如图所示.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】如图所示,△ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1)将△ABC三个顶点的横坐标都减去5,纵坐标不变,分别得到点A1、B1、C1,依次连结A1、B1、C1各点,所得△A1B1C1与△ABC的大小、形状和位置上有什么关系?
(2)将△ABC三个顶点的纵坐标都减去4,横坐标不变,分别得到点A2、B2、C2,依次连结A2、B2、C2各点,所得△A2B2C2与△ABC的大小、形状和位置上有什么关系?
【互动探索】(引发学生思考)(1)△ABC三个顶点的横坐标都减去5,纵坐标不变,就是把△ABC向左平移了5个单位得到△A1B1C1;
(2)△ABC三个顶点的纵坐标都减去4,横坐标不变,就是把△ABC向下平移了4个单位得到△A2B2C2.
【解答】(1)根据题意,得点A1(-1,3)、B1(-2,1)、C1(-4,2),所得△A1B1C1与△ABC的大小、形状完全一样,只是把△ABC向左平移了5个单位.
(2)根据题意,得点A2(4,-1)、B2(3,-3)、C2(1,-2),所得△A2B2C2与△ABC的大小、形状完全一样,只是把△ABC向下平移了4个单位.
【互动总结】(学生总结,老师点评)本题考查了坐标与图形变化—平移:向右平移a(a>0)个单位,坐标P(x,y)→P(x+a,y);向左平移a(a>0)个单位,坐标P(x,y)→P(x-a,y);向上平移b(b>0)个单位,坐标P(x,y)→P(x,y+b);向下平移b(b>0)个单位,坐标P(x,y)→P(x,y-b).
活动2 巩固练习(学生独学)
1.在平面直角坐标系中,△ABC的三个顶点坐标分别是A(4,5)、B(1,2)、C(4,2),将△ABC向左平移5个单位长度后,点A的对应点A′的坐标是( B )
A.(0,5) B.(-1,5)
C.(9,5) D.(-1,0)
2.一个三角形最初的一个顶点为A,把它先向下平移4个单位长度后的位置记为B,再向左平移3个单位长度后的位置记为C,则由A、B、C三点所组成的三角形的周长为( C )
A.7 B.14
C.12 D.15
3.如图所示,在直角坐标系中,点A的坐标为(-1,2),点C的坐标为(-3,0),将线段AC沿x轴向右平移3个单位长度,此时点A的对应点的坐标为(2,2).
4.如图所示,△OAB的顶点B的坐标为(4,0),把△OAB沿x轴向右平移得到△CDE.如果CB=1,那么OE的长为7.
活动3 拓展延伸(学生对学)
【例2】如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3.已知A(-3,1)、A1(-3,2)、A2(-3,4)、A3(-3,8);B(0,2)、B1(0,4)、B2(0,6)、B3(0,8).
(1)观察每次变换前后三角形有何变化,找出规律,按此变换规律再将△OA3B3变换成OA4B4,则点A4的坐标为______,点B4的坐标为______;
(2)若按(1)题找到的规律,将△OAB进行n次变换,得到△OAnBn,则点An的坐标是______,Bn的坐标是______.
【互动探索】(1)根据题意得出点A、B横、纵坐标的变化规律,进而得出答案;
(2)结合(1)中发现的规律得出一般公式即可得解.
【分析】(1)∵A(-3,1)、A1(-3,2)、A2(-3,4)、A3(-3,8),
∴其变化规律:横坐标为-3,纵坐标依次为20,2,22,23,…
∴A4的纵坐标为24=16,
∴A4(-3,16).
∵B(0,2)、B1(0,4)、B2(0,6)、B3(0,8),
∴其变化规律:横坐标为0,纵坐标依次为2,2×1+2,2×2+2,2×3+2,…,
∴B4的纵坐标为2×4+2=10,
∴B4(0,10).
(2)由(1)得出:An(-3,2n)、Bn(0,2n+2).
【答案】(1)(-3,16) (0,10)
(2)(-3,2n) (0,2n+2)
【互动总结】(学生总结,老师点评)此题主要考查了规律型点的坐标,根据题意得出点A、B横、纵坐标变化规律是解题关键.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
设(x,y)是原图形上的一点,经过平移后,这个点与其对应点的坐标之间有如下关系:
平移方向 平移距离 对应点的坐标
沿x轴方向 向右平移 a个单位长度(a>0) (x+a,y)
向左平移 (x-a,y)
沿y轴方向 向上平移 (x,y+a)
向下平移 (x,y-a)
练习设计
请完成本课时对应练习!
第3课时 坐标系中的点沿x轴、y轴的两次平移
教学目标
一、基本目标
1.继续探究平移既有横向又有纵向时坐标的变化特点.
2.经历沿x轴、y轴方向和综合方向平移时位置和数量的关系,通过观察、分析以及抽象、概括等过程,发现平移时坐标变化的特点.
3.通过欣赏生活中的平移图形与学生自己设计的平移图案,使学生感受数学的美.
二、重难点目标
【教学重点】
沿x轴、y轴方向和综合方向平移时位置和数量的关系.
【教学难点】
坐标变化和图形平移的关系.
教学过程
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P71~P73的内容,完成下面练习.
【3 min反馈】
1.一个图形依次沿着x轴方向、y轴方向平移后所得到图形,可以看成是由原来的图形经过一次平移得到的.
2.如图所示,在10×6的网格中,每个小方格的边长都是1个单位.将三角形ABC平移到三角形DEF的位置,下面正确的平移步骤是( A )
A.先把三角形ABC向左平移5个单位长度,再向下平移2个单位长度
B.先把三角形ABC向右平移5个单位长度,再向下平移2个单位长度
C.先把三角形ABC向左平移5个单位长度,再向上平移2个单位长度
D.先把三角形ABC向右平移5个单位长度,再向上平移2个单位长度
3.将点A(-3,-3)向右平移5个单位长度,得到点A1,再把A1向上平移4个单位长度,得到点A2,则点A2的坐标为( B )
A.(-2,-1) B.(2,1)
C.(-3,1) D.(3,1)
4.将点A(-2,5)沿x轴负方向平移6个单位长度,再将横坐标乘-2,所得点的坐标为(16,5).
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后的对应点为P′(x0+5,y0-2).
(1)已知A(-1,2)、B(-4,5)、C(-3,0),请写出A′、B′、C′的坐标;
(2)试说明△A′B′C′是如何由△ABC平移得到的;
(3)请直接写出△A′B′C′的面积.
【互动探索】(引发学生思考)(1)根据点P(x0,y0)经平移后的对应点为P′(x0+5,y0-2)可得A、B、C三点的坐标变化规律;(2)根据点的坐标的变化规律可得△ABC先向右平移5个单位,再向下平移2个单位;(3)把△A′B′C′放在一个矩形内,利用矩形的面积减去周围多余三角形的面积即可.
【解答】(1)A′(4,0)、B′(1,3)、C′(2,-2).
(2)△ABC先向右平移5个单位,再向下平移2个单位(或先向下平移2个单位,再向右平移5个单位).
(3)△A′B′C′的面积为6.
【互动总结】(学生总结,老师点评)熟练掌握平移规律是解题关键:上下平移,横坐标不变,纵坐标上加下减;左右平移,纵坐标不变,横坐标左减右加.
活动2 巩固练习(学生独学)
1.把点M(1,3)先向右平移2个单位长度,再向下平移1个单位长度后,得到的点是( A )
A.(3,2) B.(-1,4)
C.(0,5) D.(2,1)
2.如图所示,在平面直角坐标系中,△ABC经过平移后点A的对应点为点A′,则平移后点B的对应点B′的坐标为(-2,1).
3.如图所示,A、B的坐标分别为(1,0),(0,2),若将线段AB平移到线段A1B1,A1、B1的坐标分别为(2,a),(b,3), 则a+b=2.
4.已知长方形ABCD在平面直角坐标系中的位置如图所示,将长方形ABCD沿x轴向左平移到使点C与坐标原点重合后,再沿y轴向下平移到使点D与坐标原点重合,此时点B的坐标是(-5,-3).
5.如图所示的一小船,将其向左平移6个单位长度,再向下平移5个单位长度,试确定A、B、C、D、E、F、G平移后对应点的坐标,并画出平移后的图形.
解:对应点坐标分别为A′(-5,-3)、B′(-3,-4)、C′(-2,-4)、D′(-1,-3)、E′(-3,-3)、F′(-3,-1)、G′(-4,-2).描出这些对应点并按原来的顺序连结起来,可得平移后的图形,如图所示.
活动3 拓展延伸(学生对学)
【例2】在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.
(1)求下列各点的坐标:A4、A8、A10、A12;
(2)写出点A4n的坐标(n是正整数);
(3)按此移动规律,若点Am在x轴上,请用含n的代数式表示m(n是正整数);
(4)指出蚂蚁从点A2019到点A2020的移动方向.
【互动探索】(1)观察图形可知,A4、A8、A12都在x轴上,求出OA4、OA8、OA12的长度,然后写出坐标即可;(2)根据(1)中规律写出点A4n的坐标即可;(3)根据以上所求即可得出在x轴上点的变化规律以及下标为4n或4n-1;(4)根据2019÷4=504……3,可知从点A2019到点A2020的移动方向与从点A3到A4的方向一致.
【解答】(1)由图可知,A4、A8、A12…都在x轴上.
∵小蚂蚁每次移动1个单位,
∴OA4=2,OA8=4,OA12=6,
∴A4(2,0)、A8(4,0)、A12(6,0),
∴A10(5,1).
(2)根据(1)可知,OA4n的横坐标为4n÷2=2n,纵坐标为0,
∴A4n(2n,0).
(3)∵只有下标为4的倍数或比4的倍数小1的数在x轴上,而点Am在x轴上,
∴用含n的代数式表示为m=4n或m=4n-1.
(4)∵2019÷4=504……3,
∴从点A2019到点A2020的移动方向与从点A3到A4的方向一致,为向右.
【互动总结】(学生总结,老师点评)此题主要考查了点的变化规律,仔细观察图形,确定出A4n都在x轴上是解题关键.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
设(x,y)是原图形上的一点,当它沿x轴方向平移a(a>0)个单位长度,沿y轴方向平移b(b>0)个单位长度后,这个点与其对应点的坐标之间有如下关系:
平移方向和平移距离 对应点的坐标
向右平移a个单位长度,向上平移b个单位长度 (x+a,y+b)
向右平移a个单位长度,向下平移b个单位长度 (x+a,y-b)
向左平移a个单位长度,向上平移b个单位长度 (x-a,y+b)
向左平移a个单位长度,向下平移b个单位长度 (x-a,y-b)
练习设计
请完成本课时对应练习!
第1课时 平移的认识
教学目标
一、基本目标
1.认识平移,说出平移的定义,理解平移的基本内涵.
2.经历观察、分析、操作、欣赏以及抽象、概括等过程,探索图形平移的基本性质.
3.通过探究,归纳平移的定义、特征、性质,积累数学活动经验,进一步发展空间观念,增强空间想象力.
二、重难点目标
【教学重点】
理解并掌握平移的定义及性质.
【教学难点】
根据平移的性质进行简单的平移作图.
教学过程
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P65~P67的内容,完成下面练习.
【3 min反馈】
1.在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.平移不改变图形的形状和大小.
2. 一个图形和它经过平移所得的图形中,对应点所连的线段平行(或在一条直线上)且相等,对应线段平行(或在一条直线上)且相等,对应角相等.
3.下列运动属于平移的是( A )
A.急刹车时汽车在地面上的滑动
B.冷水加热中,小气泡上升为大气泡
C.随风飘动的风筝在空中的运动
D.随手抛出的彩球的运动
4.如图所示,下列每组图形中的两个三角形不是通过平移得到的是( B )
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】(教材P66例1)如图,经过平移,△ABC的顶点A移到了点D.
(1)指出平移的方向和距离;
(2)画出平移后的三角形.
【互动探索】(引发学生思考)平移的方向和距离怎么确定?(对应点从起点到终点所指的方向,对应点间的线段长度为平移距离)→画平移图形的方法是什么?
【解答】(1)如图,连结AD,平移的方向是点A到点D的方向,平移的距离是线段AD的长度.
(2)如图,分别过点B、C按射线AD的方向作线段BE、CF,使得它们与线段AD平行且相等,连结DE、DF、EF,△DEF就是△ABC平移后的图形.
【例2】如图,将等腰直角△ABC沿BC方向平移得到△A1B1C1,若BC=3,△ABC与△A1B1C1重叠部分面积为2,则BB1等于( )
A.1 B.
C. D.2
【互动探索】(引发学生思考)观察重叠部分是哪种特殊三角形?由它的面积可以求出哪条边的长?
【分析】设B1C=2x,根据等腰直角三角形和平移的性质可知,重叠部分为等腰直角三角形,则B1C边上的高为x,∴×x×2x=2,解得x=(舍去负值),∴B1C=2,∴BB1=BC-B1C=.
【答案】B
【互动总结】(学生总结,老师点评)本题考查了等腰直角三角形的性质和平移的性质,关键是判断重叠部分为等腰直角三角形,利用等腰直角三角形的性质和重叠部分面积列出方程,求出重叠部分的底边长.
活动2 巩固练习(学生独学)
1.下列说法正确的是( B )
A.两个全等的图形可看作其中一个是由另一个平移得到的
B.由平移得到的两个图形对应点连线互相平行(或共线)
C.由平移得到的两个等腰三角形周长一定相等,但面积未必相等
D.边长相等的两个正方形一定可以通过平移得到
2.下列现象:①电风扇的转动;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上瓶装饮料的移动.其中属于平移的是②④.(填序号)
3.如图所示,一张白色正方形纸片的边长是10 cm,被两张宽为2 cm的纸条(阴影部分)分为四个白色的长方形部分,请你利用平移的知识求出图中白色部分的面积.
解:把图中的阴影部分平移到正方形纸片相邻的两边上,这时图中的四个白色长方形变成了一个正方形,且边长为10-2=8(cm),则面积为82=64(cm2),故图中白色部分的面积为64 cm2.
活动3 拓展延伸(学生对学)
【例3】如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移线段BE的距离,就得到此图形,下列结论正确的有( )
①AC∥DF;②HE=5;③CF=5;④阴影部分面积为.
A.1个 B.2个
C.3个 D.4个
【互动探索】根据平移的性质得出对应点所连的线段平行且相等,对应角相等,对应线段平行且相等,阴影部分和三角形面积之间的关系,结合图形与所给的结论即可得出答案.
【分析】①由对应线段平行可得AC∥DF,正确;②由对应线段相等可得AB=DE=8,则HE=DE-DH=8-3=5,正确;③平移的距离CF=BE=5,正确;④S四边形HDFC=S梯形ABEH=(AB+EH)·BE=×(8+5)×5=,错误.
【答案】C
【互动总结】(学生总结,老师点评)本题考查平移的基本性质:(1)平移不改变图形的形状和大小;(2)对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
1.平移的定义
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
2.平移的性质
一个图形和它经过平移所得的图形中,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等,对应角相等.
3.简单的平移作图
练习设计
请完成本课时对应练习!
第2课时 坐标系中的点沿x轴、y轴的一次平移
教学目标
一、基本目标
1.进一步理解平移的意义和平移的性质.
2.通过“变化的鱼”探究横向(或纵向)平移一次,其坐标变化的规律,认识图形变换与坐标之间的内在联系.
3.理解并掌握图形平移在平面直角坐标系中的坐标变化规律,即:向右平移几,就是横坐标加几;向左平移几,就是横坐标减几;向上平移几,就是纵坐标加几;向下平移几,就是纵坐标减几.
二、重难点目标
【教学重点】
理解和掌握直角坐标系中图形的坐标变化规律.
【教学难点】
对图形平移在平面直角坐标系中的坐标变化规律的探究.
教学过程
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P68~P69的内容,完成下面练习.
【3 min反馈】
1.在平面直角坐标系中,如果把图形中点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原来的图形沿着x轴向右(或向左)平移a个单位长度.
2.在平面直角坐标系中,如果把图形中点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原来的图形沿着y轴向上(或向下)平移a个单位长度.
3.如果一个图案沿x轴负方向平移3个单位长度,那么这个图案上的点的坐标变化为( B )
A.横坐标不变,纵坐标减少3个单位长度
B.纵坐标不变,横坐标减少3个单位长度
C.横、纵坐标都没有变化
D.横、纵坐标都减少3个单位长度
4.点M(-2,5)是由点N向上平移3个单位长度得到的,则点N的坐标为( A )
A.(-2,2) B.(-5,5)
C.(-2,8) D.(1,5)
5.如图所示,经过平移,小船上的点A移到了点B,作出平移后的小船.
解:如图所示.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】如图所示,△ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1)将△ABC三个顶点的横坐标都减去5,纵坐标不变,分别得到点A1、B1、C1,依次连结A1、B1、C1各点,所得△A1B1C1与△ABC的大小、形状和位置上有什么关系?
(2)将△ABC三个顶点的纵坐标都减去4,横坐标不变,分别得到点A2、B2、C2,依次连结A2、B2、C2各点,所得△A2B2C2与△ABC的大小、形状和位置上有什么关系?
【互动探索】(引发学生思考)(1)△ABC三个顶点的横坐标都减去5,纵坐标不变,就是把△ABC向左平移了5个单位得到△A1B1C1;
(2)△ABC三个顶点的纵坐标都减去4,横坐标不变,就是把△ABC向下平移了4个单位得到△A2B2C2.
【解答】(1)根据题意,得点A1(-1,3)、B1(-2,1)、C1(-4,2),所得△A1B1C1与△ABC的大小、形状完全一样,只是把△ABC向左平移了5个单位.
(2)根据题意,得点A2(4,-1)、B2(3,-3)、C2(1,-2),所得△A2B2C2与△ABC的大小、形状完全一样,只是把△ABC向下平移了4个单位.
【互动总结】(学生总结,老师点评)本题考查了坐标与图形变化—平移:向右平移a(a>0)个单位,坐标P(x,y)→P(x+a,y);向左平移a(a>0)个单位,坐标P(x,y)→P(x-a,y);向上平移b(b>0)个单位,坐标P(x,y)→P(x,y+b);向下平移b(b>0)个单位,坐标P(x,y)→P(x,y-b).
活动2 巩固练习(学生独学)
1.在平面直角坐标系中,△ABC的三个顶点坐标分别是A(4,5)、B(1,2)、C(4,2),将△ABC向左平移5个单位长度后,点A的对应点A′的坐标是( B )
A.(0,5) B.(-1,5)
C.(9,5) D.(-1,0)
2.一个三角形最初的一个顶点为A,把它先向下平移4个单位长度后的位置记为B,再向左平移3个单位长度后的位置记为C,则由A、B、C三点所组成的三角形的周长为( C )
A.7 B.14
C.12 D.15
3.如图所示,在直角坐标系中,点A的坐标为(-1,2),点C的坐标为(-3,0),将线段AC沿x轴向右平移3个单位长度,此时点A的对应点的坐标为(2,2).
4.如图所示,△OAB的顶点B的坐标为(4,0),把△OAB沿x轴向右平移得到△CDE.如果CB=1,那么OE的长为7.
活动3 拓展延伸(学生对学)
【例2】如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3.已知A(-3,1)、A1(-3,2)、A2(-3,4)、A3(-3,8);B(0,2)、B1(0,4)、B2(0,6)、B3(0,8).
(1)观察每次变换前后三角形有何变化,找出规律,按此变换规律再将△OA3B3变换成OA4B4,则点A4的坐标为______,点B4的坐标为______;
(2)若按(1)题找到的规律,将△OAB进行n次变换,得到△OAnBn,则点An的坐标是______,Bn的坐标是______.
【互动探索】(1)根据题意得出点A、B横、纵坐标的变化规律,进而得出答案;
(2)结合(1)中发现的规律得出一般公式即可得解.
【分析】(1)∵A(-3,1)、A1(-3,2)、A2(-3,4)、A3(-3,8),
∴其变化规律:横坐标为-3,纵坐标依次为20,2,22,23,…
∴A4的纵坐标为24=16,
∴A4(-3,16).
∵B(0,2)、B1(0,4)、B2(0,6)、B3(0,8),
∴其变化规律:横坐标为0,纵坐标依次为2,2×1+2,2×2+2,2×3+2,…,
∴B4的纵坐标为2×4+2=10,
∴B4(0,10).
(2)由(1)得出:An(-3,2n)、Bn(0,2n+2).
【答案】(1)(-3,16) (0,10)
(2)(-3,2n) (0,2n+2)
【互动总结】(学生总结,老师点评)此题主要考查了规律型点的坐标,根据题意得出点A、B横、纵坐标变化规律是解题关键.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
设(x,y)是原图形上的一点,经过平移后,这个点与其对应点的坐标之间有如下关系:
平移方向 平移距离 对应点的坐标
沿x轴方向 向右平移 a个单位长度(a>0) (x+a,y)
向左平移 (x-a,y)
沿y轴方向 向上平移 (x,y+a)
向下平移 (x,y-a)
练习设计
请完成本课时对应练习!
第3课时 坐标系中的点沿x轴、y轴的两次平移
教学目标
一、基本目标
1.继续探究平移既有横向又有纵向时坐标的变化特点.
2.经历沿x轴、y轴方向和综合方向平移时位置和数量的关系,通过观察、分析以及抽象、概括等过程,发现平移时坐标变化的特点.
3.通过欣赏生活中的平移图形与学生自己设计的平移图案,使学生感受数学的美.
二、重难点目标
【教学重点】
沿x轴、y轴方向和综合方向平移时位置和数量的关系.
【教学难点】
坐标变化和图形平移的关系.
教学过程
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P71~P73的内容,完成下面练习.
【3 min反馈】
1.一个图形依次沿着x轴方向、y轴方向平移后所得到图形,可以看成是由原来的图形经过一次平移得到的.
2.如图所示,在10×6的网格中,每个小方格的边长都是1个单位.将三角形ABC平移到三角形DEF的位置,下面正确的平移步骤是( A )
A.先把三角形ABC向左平移5个单位长度,再向下平移2个单位长度
B.先把三角形ABC向右平移5个单位长度,再向下平移2个单位长度
C.先把三角形ABC向左平移5个单位长度,再向上平移2个单位长度
D.先把三角形ABC向右平移5个单位长度,再向上平移2个单位长度
3.将点A(-3,-3)向右平移5个单位长度,得到点A1,再把A1向上平移4个单位长度,得到点A2,则点A2的坐标为( B )
A.(-2,-1) B.(2,1)
C.(-3,1) D.(3,1)
4.将点A(-2,5)沿x轴负方向平移6个单位长度,再将横坐标乘-2,所得点的坐标为(16,5).
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后的对应点为P′(x0+5,y0-2).
(1)已知A(-1,2)、B(-4,5)、C(-3,0),请写出A′、B′、C′的坐标;
(2)试说明△A′B′C′是如何由△ABC平移得到的;
(3)请直接写出△A′B′C′的面积.
【互动探索】(引发学生思考)(1)根据点P(x0,y0)经平移后的对应点为P′(x0+5,y0-2)可得A、B、C三点的坐标变化规律;(2)根据点的坐标的变化规律可得△ABC先向右平移5个单位,再向下平移2个单位;(3)把△A′B′C′放在一个矩形内,利用矩形的面积减去周围多余三角形的面积即可.
【解答】(1)A′(4,0)、B′(1,3)、C′(2,-2).
(2)△ABC先向右平移5个单位,再向下平移2个单位(或先向下平移2个单位,再向右平移5个单位).
(3)△A′B′C′的面积为6.
【互动总结】(学生总结,老师点评)熟练掌握平移规律是解题关键:上下平移,横坐标不变,纵坐标上加下减;左右平移,纵坐标不变,横坐标左减右加.
活动2 巩固练习(学生独学)
1.把点M(1,3)先向右平移2个单位长度,再向下平移1个单位长度后,得到的点是( A )
A.(3,2) B.(-1,4)
C.(0,5) D.(2,1)
2.如图所示,在平面直角坐标系中,△ABC经过平移后点A的对应点为点A′,则平移后点B的对应点B′的坐标为(-2,1).
3.如图所示,A、B的坐标分别为(1,0),(0,2),若将线段AB平移到线段A1B1,A1、B1的坐标分别为(2,a),(b,3), 则a+b=2.
4.已知长方形ABCD在平面直角坐标系中的位置如图所示,将长方形ABCD沿x轴向左平移到使点C与坐标原点重合后,再沿y轴向下平移到使点D与坐标原点重合,此时点B的坐标是(-5,-3).
5.如图所示的一小船,将其向左平移6个单位长度,再向下平移5个单位长度,试确定A、B、C、D、E、F、G平移后对应点的坐标,并画出平移后的图形.
解:对应点坐标分别为A′(-5,-3)、B′(-3,-4)、C′(-2,-4)、D′(-1,-3)、E′(-3,-3)、F′(-3,-1)、G′(-4,-2).描出这些对应点并按原来的顺序连结起来,可得平移后的图形,如图所示.
活动3 拓展延伸(学生对学)
【例2】在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.
(1)求下列各点的坐标:A4、A8、A10、A12;
(2)写出点A4n的坐标(n是正整数);
(3)按此移动规律,若点Am在x轴上,请用含n的代数式表示m(n是正整数);
(4)指出蚂蚁从点A2019到点A2020的移动方向.
【互动探索】(1)观察图形可知,A4、A8、A12都在x轴上,求出OA4、OA8、OA12的长度,然后写出坐标即可;(2)根据(1)中规律写出点A4n的坐标即可;(3)根据以上所求即可得出在x轴上点的变化规律以及下标为4n或4n-1;(4)根据2019÷4=504……3,可知从点A2019到点A2020的移动方向与从点A3到A4的方向一致.
【解答】(1)由图可知,A4、A8、A12…都在x轴上.
∵小蚂蚁每次移动1个单位,
∴OA4=2,OA8=4,OA12=6,
∴A4(2,0)、A8(4,0)、A12(6,0),
∴A10(5,1).
(2)根据(1)可知,OA4n的横坐标为4n÷2=2n,纵坐标为0,
∴A4n(2n,0).
(3)∵只有下标为4的倍数或比4的倍数小1的数在x轴上,而点Am在x轴上,
∴用含n的代数式表示为m=4n或m=4n-1.
(4)∵2019÷4=504……3,
∴从点A2019到点A2020的移动方向与从点A3到A4的方向一致,为向右.
【互动总结】(学生总结,老师点评)此题主要考查了点的变化规律,仔细观察图形,确定出A4n都在x轴上是解题关键.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
设(x,y)是原图形上的一点,当它沿x轴方向平移a(a>0)个单位长度,沿y轴方向平移b(b>0)个单位长度后,这个点与其对应点的坐标之间有如下关系:
平移方向和平移距离 对应点的坐标
向右平移a个单位长度,向上平移b个单位长度 (x+a,y+b)
向右平移a个单位长度,向下平移b个单位长度 (x+a,y-b)
向左平移a个单位长度,向上平移b个单位长度 (x-a,y+b)
向左平移a个单位长度,向下平移b个单位长度 (x-a,y-b)
练习设计
请完成本课时对应练习!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
