4.6利用相似三角形测高 同步练习2021-2022学年北师大版九年级数学上册(Word版含答案)
文档属性
| 名称 | 4.6利用相似三角形测高 同步练习2021-2022学年北师大版九年级数学上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 314.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 08:32:41 | ||
图片预览

文档简介
2021-2022学年北师大版九年级数学上册《4.6利用相似三角形测高》同步练习(附答案)
1.相邻两根电杆都用钢索在地面上固定,如图,一根电杆钢索系在离地面4米处,另一根电杆钢索系在离地面6米处,两根电线杆的钢索都有一根固定在另一根电线杆底部,则中间两根钢索相交处点P离地面( )
A.2.4米 B.8米
C.3米 D.必须知道两根电线杆的距离才能求出点P离地面距离
2.根据中国人民政治协商会议第一届全体会议主席团1949年9月27日公布的国旗制法说明,我国五种规格的国旗旗面为相似矩形,已知一号国旗的标准尺寸是长288cm,高192cm,则如图国旗尺寸不符合标准的是( )
A. B.
C. D.
3.如图,一位同学通过调整自己的位置,设法使三角板DEF的斜边DF保持水平,并且边DE与点B在同一直线上,已知两条边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB为 m.
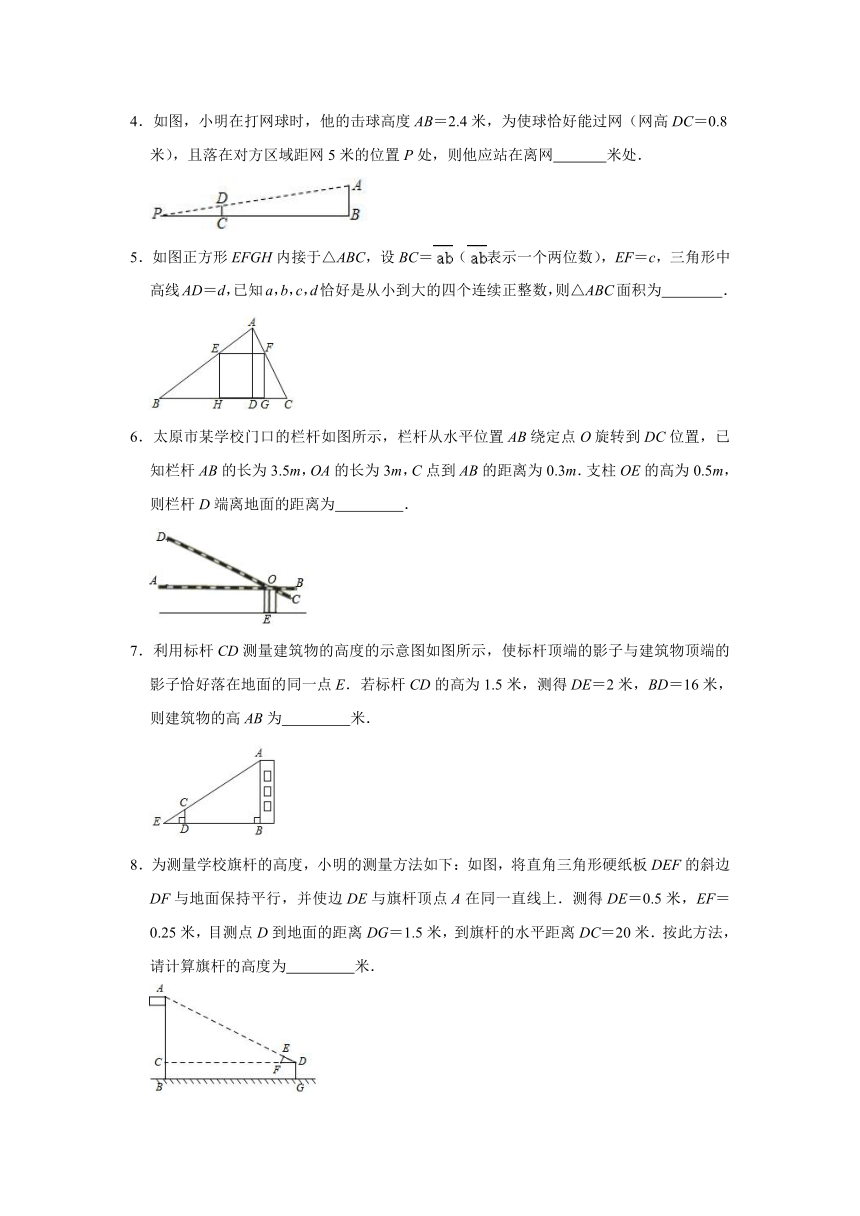
4.如图,小明在打网球时,他的击球高度AB=2.4米,为使球恰好能过网(网高DC=0.8米),且落在对方区域距网5米的位置P处,则他应站在离网 米处.
5.如图正方形EFGH内接于△ABC,设BC=(表示一个两位数),EF=c,三角形中高线AD=d,已知a,b,c,d恰好是从小到大的四个连续正整数,则△ABC面积为 .
6.太原市某学校门口的栏杆如图所示,栏杆从水平位置AB绕定点O旋转到DC位置,已知栏杆AB的长为3.5m,OA的长为3m,C点到AB的距离为0.3m.支柱OE的高为0.5m,则栏杆D端离地面的距离为 .
7.利用标杆CD测量建筑物的高度的示意图如图所示,使标杆顶端的影子与建筑物顶端的影子恰好落在地面的同一点E.若标杆CD的高为1.5米,测得DE=2米,BD=16米,则建筑物的高AB为 米.
8.为测量学校旗杆的高度,小明的测量方法如下:如图,将直角三角形硬纸板DEF的斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上.测得DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米.按此方法,请计算旗杆的高度为 米.
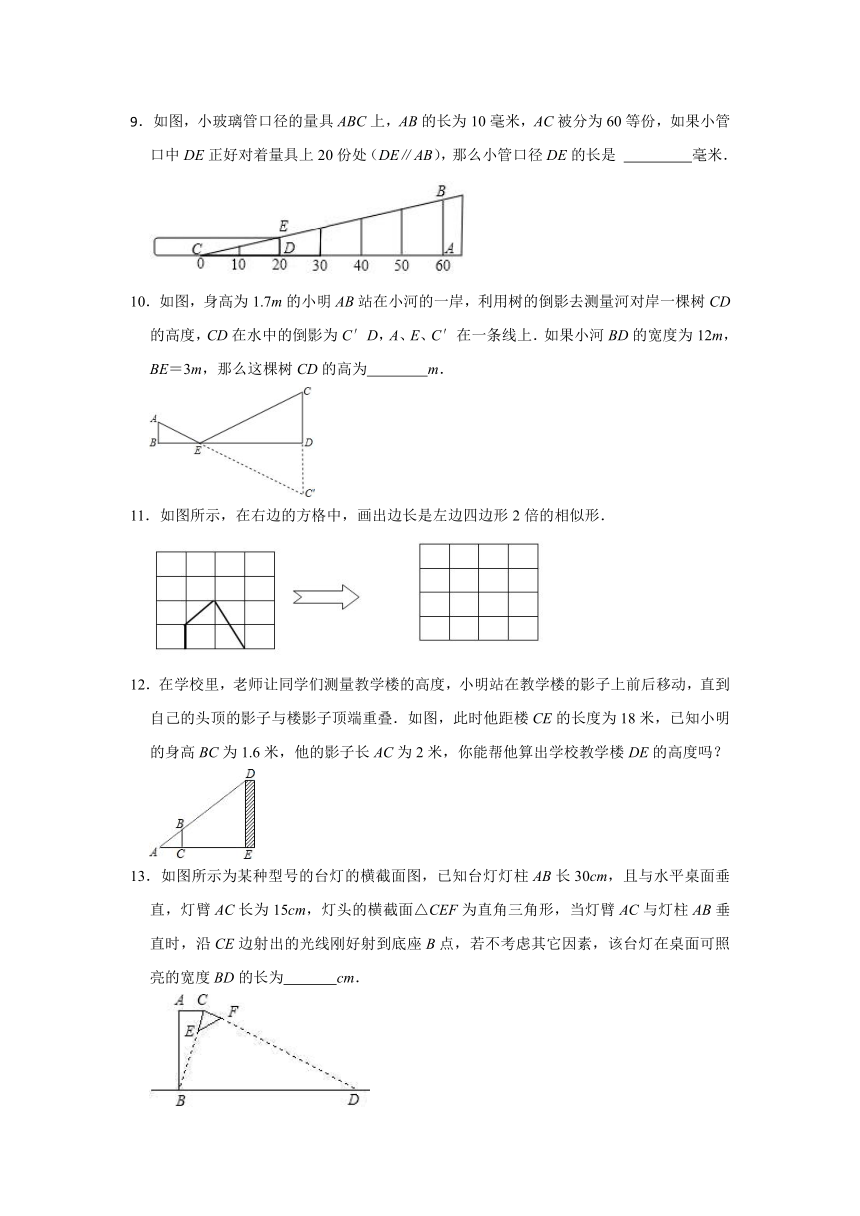
如图,小玻璃管口径的量具ABC上,AB的长为10毫米,AC被分为60等份,如果小管口中DE正好对着量具上20份处(DE∥AB),那么小管口径DE的长是 毫米.
10.如图,身高为1.7m的小明AB站在小河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A、E、C′在一条线上.如果小河BD的宽度为12m,BE=3m,那么这棵树CD的高为 m.
11.如图所示,在右边的方格中,画出边长是左边四边形2倍的相似形.
12.在学校里,老师让同学们测量教学楼的高度,小明站在教学楼的影子上前后移动,直到自己的头顶的影子与楼影子顶端重叠.如图,此时他距楼CE的长度为18米,已知小明的身高BC为1.6米,他的影子长AC为2米,你能帮他算出学校教学楼DE的高度吗?
13.如图所示为某种型号的台灯的横截面图,已知台灯灯柱AB长30cm,且与水平桌面垂直,灯臂AC长为15cm,灯头的横截面△CEF为直角三角形,当灯臂AC与灯柱AB垂直时,沿CE边射出的光线刚好射到底座B点,若不考虑其它因素,该台灯在桌面可照亮的宽度BD的长为 cm.
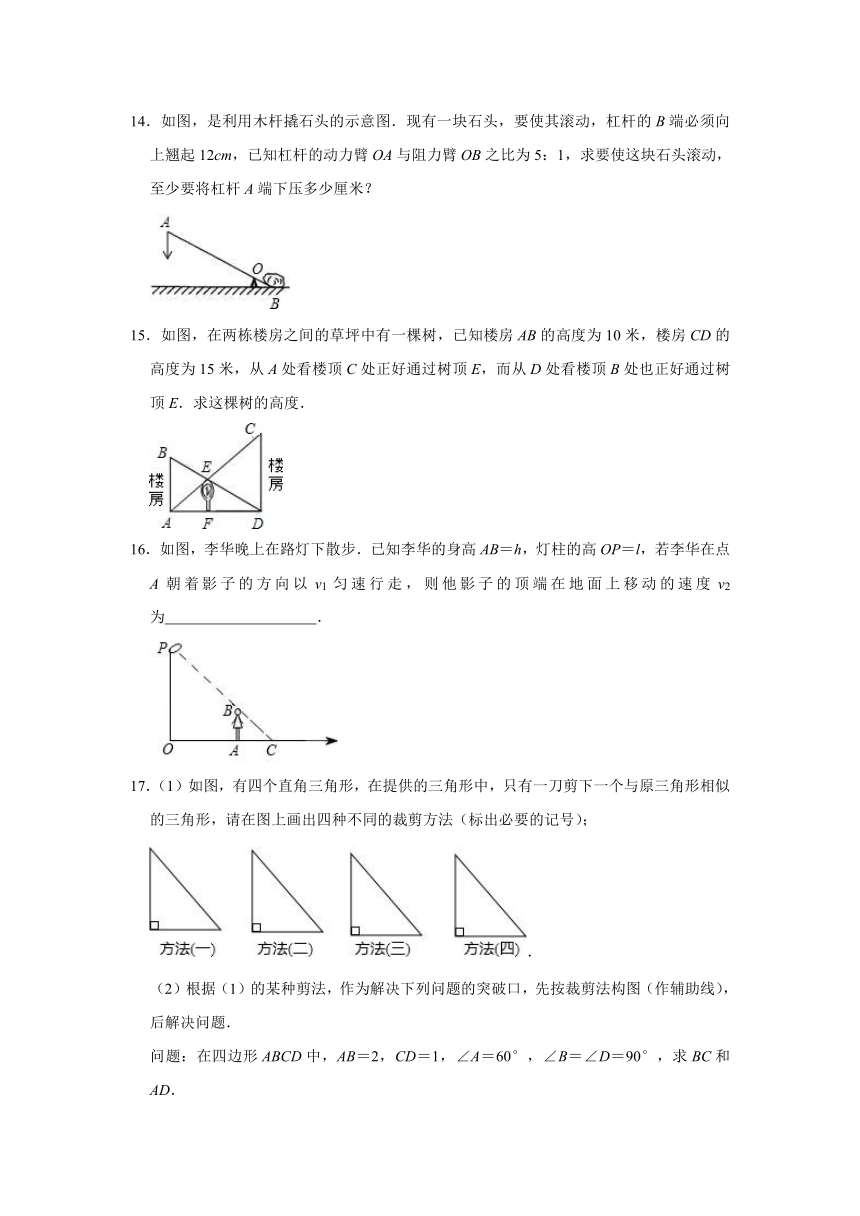
14.如图,是利用木杆撬石头的示意图.现有一块石头,要使其滚动,杠杆的B端必须向上翘起12cm,已知杠杆的动力臂OA与阻力臂OB之比为5:1,求要使这块石头滚动,至少要将杠杆A端下压多少厘米?
15.如图,在两栋楼房之间的草坪中有一棵树,已知楼房AB的高度为10米,楼房CD的高度为15米,从A处看楼顶C处正好通过树顶E,而从D处看楼顶B处也正好通过树顶E.求这棵树的高度.
16.如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=l,若李华在点A朝着影子的方向以v1匀速行走,则他影子的顶端在地面上移动的速度v2为 .
17.(1)如图,有四个直角三角形,在提供的三角形中,只有一刀剪下一个与原三角形相似的三角形,请在图上画出四种不同的裁剪方法(标出必要的记号);
.
(2)根据(1)的某种剪法,作为解决下列问题的突破口,先按裁剪法构图(作辅助线),后解决问题.
问题:在四边形ABCD中,AB=2,CD=1,∠A=60°,∠B=∠D=90°,求BC和AD.
.
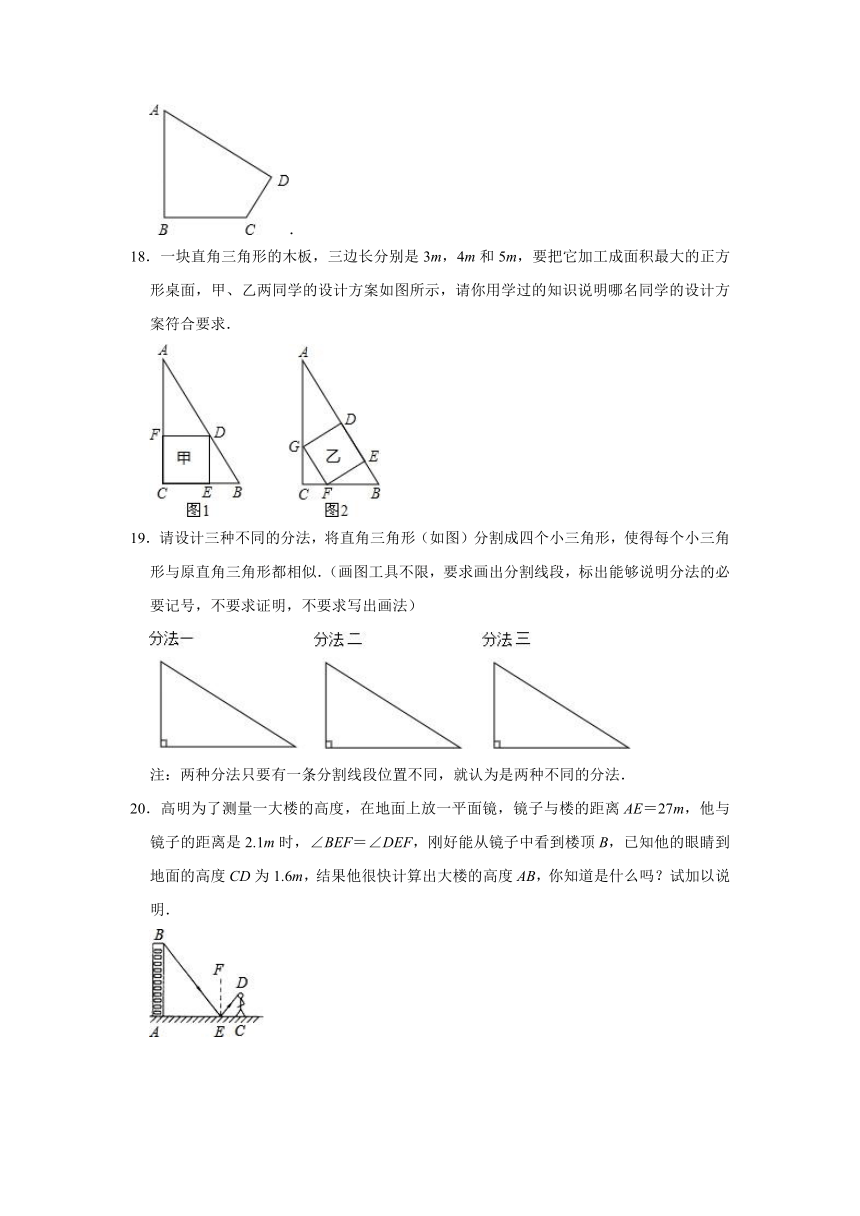
18.一块直角三角形的木板,三边长分别是3m,4m和5m,要把它加工成面积最大的正方形桌面,甲、乙两同学的设计方案如图所示,请你用学过的知识说明哪名同学的设计方案符合要求.
19.请设计三种不同的分法,将直角三角形(如图)分割成四个小三角形,使得每个小三角形与原直角三角形都相似.(画图工具不限,要求画出分割线段,标出能够说明分法的必要记号,不要求证明,不要求写出画法)
注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.
20.高明为了测量一大楼的高度,在地面上放一平面镜,镜子与楼的距离AE=27m,他与镜子的距离是2.1m时,∠BEF=∠DEF,刚好能从镜子中看到楼顶B,已知他的眼睛到地面的高度CD为1.6m,结果他很快计算出大楼的高度AB,你知道是什么吗?试加以说明.
参考答案
1.解:作PE⊥BC于E.
∵CD∥AB,
∴△APB∽△CDP,
∴====,
∵CD∥PE,
∴△BPE∽△BDC,
∴=,
∴=,
解得PE=2.4.
故选:A.
2.解:288:192=3:2.
A、由于240:160=3:2,所以该国旗尺寸符合标准,故本选项不符合题意.
B、由于160:120=4:3,所以该国旗尺寸不符合标准,故本选项符合题意.
C、由于144:96=3:2,所以该国旗尺寸符合标准,故本选项不符合题意.
D、由于96:64=3:2,所以该国旗尺寸符合标准,故本选项不符合题意.
故选:B.
3.解:∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB
∴,
∵DE=0.4m,EF=0.2m,CD=8m,
∴,
∴CB=4(m),
∴AB=AC+BC=1.5+4=5.5(米).
故答案为:5.5.
4.解:设他应站在离网的x米处,
根据题意得:,
解得:x=10.
故答案为:10.
5.解:a、b、c、d为连续四个整数故可设为a,a+1,a+2,a+3,
∵BC=,
∴BC=11a+1,
∵四边形EFGH是正方形,
∴EF∥BC,
∴△AEF∽△ABC,
∴=,
即=,
解关于a的方程,得
a1=1,a2=5,
经检验1和5是原分式方程的解,
∴S△ABC=BC×AD=24,或S△ABC=BC×AD=224,
故答案为:24或224.
6.解:过D作DG⊥AB于G,过C作CH⊥AB于H,
则DG∥CH,
∴△ODG∽△OCH,
∴=,
∵栏杆从水平位置AB绕固定点O旋转到位置DC,
∴CD=AB=3.5m,OD=OA=3m,CH=0.3m,
∴OC=0.5m,
∴=,
∴DG=1.8m,
∵OE=0.5m,
∴栏杆D端离地面的距离为1.8+0.5=2.3m.
故答案是:2.3m.
7.解:∵AB∥CD,
∴△EBA∽△ECD,
∴,即,
∴AB=13.5(米).
故答案为:13.5
8.解:由题意得:∠DEF=∠DCA=90°,∠EDF=∠CDA,
∴△DEF∽△DCA,
则=,即=,
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(米),
即旗杆的高度为11.5米;
故答案为:11.5.
9.解:∵DE∥AB
∴△CDE∽△CAB
∴CD:CA=DE:AB
∴20:60=DE:10
∴DE=毫米
∴小管口径DE的长是毫米.
故答案为:
10.解:∵AB,CD均垂直于地面,所以AB∥CD,
∴△ABE∽△C′DE,
∵CD在水中的倒影为C′D,
∴△ABE∽△C′DE,
∴=,
又∵AB=1.7m,BE=3m,BD=12m,
∴=,
∴CD=5.1(m),
故答案为:5.1.
11.解:
12.解:∵BC⊥AE,DE⊥AE,
可得△ABC∽△ADE,
∴,即=,
即,
∴DE=16(米).
13.解:∵AB⊥BD,AC⊥AB,
∴AC∥BD.
∴∠ACB=∠DBC.
∵∠A=∠BCD=90°,
∴△ABC∽△CDB.
∴.
∴BC2=AC BD.
在Rt△ABC中,BC2=AC2+AB2=152+302=1125,
∴15BD=1125.
∴BD=75(cm).
14.解:
∵∠ACO=∠BDO=90°,∠AOC=∠BOD,
∴△ACO∽△BDO,
=,
=
解得AC=60cm.
答:至少要将杠杆A端下压60cm.
15.解:∵AB∥CD,
∴△ABE∽△CDE,
∴==,
∵EF∥AB,
∴△FDE∽△ADB,
∴==,
∵AB=10,
∴EF=6.
答:这棵树的高度为6米.
16.解:设李华由A到A′,身高为A′B′,A′C′代表其影长(如图).
∵AB∥PO,
∴△CBA∽△CPO,
∴,
即,
∴,
同理可得:,
∴,
∴,
当李华从A走到A'的时候,他的影子也从C移到C′,因此速度与路程成正比,
∴,
所以人影顶端在地面上移动的速度为.
故答案为:.
17.解:(1)如图,作垂线或平行线;
(2)如图,作DE⊥AB,CF⊥DE,垂足为E、F,
∵∠A=60°,∠B=∠D=90°,
∴∠BCD=360°﹣∠A﹣∠B﹣∠D=′120°,
在Rt△CDF中,CD=1,∠DCF=∠BCD﹣∠BCF=30°,
DF=,CF=;
∴BE=CF=,AE=AB﹣BE=2﹣;
在Rt△ADE中,∠ADE=90°﹣∠CDF=30°,
∴DE=2﹣,
BC=EF=DE﹣DF=2﹣2,
AD=4﹣.
18.解:图1中,∵△AFD∽△ACB,
∴=,即=,
解得:FD=;
图2中,过点C作CM⊥AB于点M,如图所示:
CM==,设正方形的边长为x,
∵GF∥AB,
∴=,即=,
解得:x=,
∵>,
∴甲同学的设计方案符合要求.
19.解:所作图形如下:
20.解:∵反射角等于入射角,
∴∠BEA=∠DEC.
又∵AB⊥AC,DC⊥AC,
∴∠BAE=∠DCE=90°,
∴△ABE∽△CDE,
∴,
=,
解得AB=m.
答:楼高为m.
1.相邻两根电杆都用钢索在地面上固定,如图,一根电杆钢索系在离地面4米处,另一根电杆钢索系在离地面6米处,两根电线杆的钢索都有一根固定在另一根电线杆底部,则中间两根钢索相交处点P离地面( )
A.2.4米 B.8米
C.3米 D.必须知道两根电线杆的距离才能求出点P离地面距离
2.根据中国人民政治协商会议第一届全体会议主席团1949年9月27日公布的国旗制法说明,我国五种规格的国旗旗面为相似矩形,已知一号国旗的标准尺寸是长288cm,高192cm,则如图国旗尺寸不符合标准的是( )
A. B.
C. D.
3.如图,一位同学通过调整自己的位置,设法使三角板DEF的斜边DF保持水平,并且边DE与点B在同一直线上,已知两条边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB为 m.
4.如图,小明在打网球时,他的击球高度AB=2.4米,为使球恰好能过网(网高DC=0.8米),且落在对方区域距网5米的位置P处,则他应站在离网 米处.
5.如图正方形EFGH内接于△ABC,设BC=(表示一个两位数),EF=c,三角形中高线AD=d,已知a,b,c,d恰好是从小到大的四个连续正整数,则△ABC面积为 .
6.太原市某学校门口的栏杆如图所示,栏杆从水平位置AB绕定点O旋转到DC位置,已知栏杆AB的长为3.5m,OA的长为3m,C点到AB的距离为0.3m.支柱OE的高为0.5m,则栏杆D端离地面的距离为 .
7.利用标杆CD测量建筑物的高度的示意图如图所示,使标杆顶端的影子与建筑物顶端的影子恰好落在地面的同一点E.若标杆CD的高为1.5米,测得DE=2米,BD=16米,则建筑物的高AB为 米.
8.为测量学校旗杆的高度,小明的测量方法如下:如图,将直角三角形硬纸板DEF的斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上.测得DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米.按此方法,请计算旗杆的高度为 米.
如图,小玻璃管口径的量具ABC上,AB的长为10毫米,AC被分为60等份,如果小管口中DE正好对着量具上20份处(DE∥AB),那么小管口径DE的长是 毫米.
10.如图,身高为1.7m的小明AB站在小河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A、E、C′在一条线上.如果小河BD的宽度为12m,BE=3m,那么这棵树CD的高为 m.
11.如图所示,在右边的方格中,画出边长是左边四边形2倍的相似形.
12.在学校里,老师让同学们测量教学楼的高度,小明站在教学楼的影子上前后移动,直到自己的头顶的影子与楼影子顶端重叠.如图,此时他距楼CE的长度为18米,已知小明的身高BC为1.6米,他的影子长AC为2米,你能帮他算出学校教学楼DE的高度吗?
13.如图所示为某种型号的台灯的横截面图,已知台灯灯柱AB长30cm,且与水平桌面垂直,灯臂AC长为15cm,灯头的横截面△CEF为直角三角形,当灯臂AC与灯柱AB垂直时,沿CE边射出的光线刚好射到底座B点,若不考虑其它因素,该台灯在桌面可照亮的宽度BD的长为 cm.
14.如图,是利用木杆撬石头的示意图.现有一块石头,要使其滚动,杠杆的B端必须向上翘起12cm,已知杠杆的动力臂OA与阻力臂OB之比为5:1,求要使这块石头滚动,至少要将杠杆A端下压多少厘米?
15.如图,在两栋楼房之间的草坪中有一棵树,已知楼房AB的高度为10米,楼房CD的高度为15米,从A处看楼顶C处正好通过树顶E,而从D处看楼顶B处也正好通过树顶E.求这棵树的高度.
16.如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=l,若李华在点A朝着影子的方向以v1匀速行走,则他影子的顶端在地面上移动的速度v2为 .
17.(1)如图,有四个直角三角形,在提供的三角形中,只有一刀剪下一个与原三角形相似的三角形,请在图上画出四种不同的裁剪方法(标出必要的记号);
.
(2)根据(1)的某种剪法,作为解决下列问题的突破口,先按裁剪法构图(作辅助线),后解决问题.
问题:在四边形ABCD中,AB=2,CD=1,∠A=60°,∠B=∠D=90°,求BC和AD.
.
18.一块直角三角形的木板,三边长分别是3m,4m和5m,要把它加工成面积最大的正方形桌面,甲、乙两同学的设计方案如图所示,请你用学过的知识说明哪名同学的设计方案符合要求.
19.请设计三种不同的分法,将直角三角形(如图)分割成四个小三角形,使得每个小三角形与原直角三角形都相似.(画图工具不限,要求画出分割线段,标出能够说明分法的必要记号,不要求证明,不要求写出画法)
注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.
20.高明为了测量一大楼的高度,在地面上放一平面镜,镜子与楼的距离AE=27m,他与镜子的距离是2.1m时,∠BEF=∠DEF,刚好能从镜子中看到楼顶B,已知他的眼睛到地面的高度CD为1.6m,结果他很快计算出大楼的高度AB,你知道是什么吗?试加以说明.
参考答案
1.解:作PE⊥BC于E.
∵CD∥AB,
∴△APB∽△CDP,
∴====,
∵CD∥PE,
∴△BPE∽△BDC,
∴=,
∴=,
解得PE=2.4.
故选:A.
2.解:288:192=3:2.
A、由于240:160=3:2,所以该国旗尺寸符合标准,故本选项不符合题意.
B、由于160:120=4:3,所以该国旗尺寸不符合标准,故本选项符合题意.
C、由于144:96=3:2,所以该国旗尺寸符合标准,故本选项不符合题意.
D、由于96:64=3:2,所以该国旗尺寸符合标准,故本选项不符合题意.
故选:B.
3.解:∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB
∴,
∵DE=0.4m,EF=0.2m,CD=8m,
∴,
∴CB=4(m),
∴AB=AC+BC=1.5+4=5.5(米).
故答案为:5.5.
4.解:设他应站在离网的x米处,
根据题意得:,
解得:x=10.
故答案为:10.
5.解:a、b、c、d为连续四个整数故可设为a,a+1,a+2,a+3,
∵BC=,
∴BC=11a+1,
∵四边形EFGH是正方形,
∴EF∥BC,
∴△AEF∽△ABC,
∴=,
即=,
解关于a的方程,得
a1=1,a2=5,
经检验1和5是原分式方程的解,
∴S△ABC=BC×AD=24,或S△ABC=BC×AD=224,
故答案为:24或224.
6.解:过D作DG⊥AB于G,过C作CH⊥AB于H,
则DG∥CH,
∴△ODG∽△OCH,
∴=,
∵栏杆从水平位置AB绕固定点O旋转到位置DC,
∴CD=AB=3.5m,OD=OA=3m,CH=0.3m,
∴OC=0.5m,
∴=,
∴DG=1.8m,
∵OE=0.5m,
∴栏杆D端离地面的距离为1.8+0.5=2.3m.
故答案是:2.3m.
7.解:∵AB∥CD,
∴△EBA∽△ECD,
∴,即,
∴AB=13.5(米).
故答案为:13.5
8.解:由题意得:∠DEF=∠DCA=90°,∠EDF=∠CDA,
∴△DEF∽△DCA,
则=,即=,
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(米),
即旗杆的高度为11.5米;
故答案为:11.5.
9.解:∵DE∥AB
∴△CDE∽△CAB
∴CD:CA=DE:AB
∴20:60=DE:10
∴DE=毫米
∴小管口径DE的长是毫米.
故答案为:
10.解:∵AB,CD均垂直于地面,所以AB∥CD,
∴△ABE∽△C′DE,
∵CD在水中的倒影为C′D,
∴△ABE∽△C′DE,
∴=,
又∵AB=1.7m,BE=3m,BD=12m,
∴=,
∴CD=5.1(m),
故答案为:5.1.
11.解:
12.解:∵BC⊥AE,DE⊥AE,
可得△ABC∽△ADE,
∴,即=,
即,
∴DE=16(米).
13.解:∵AB⊥BD,AC⊥AB,
∴AC∥BD.
∴∠ACB=∠DBC.
∵∠A=∠BCD=90°,
∴△ABC∽△CDB.
∴.
∴BC2=AC BD.
在Rt△ABC中,BC2=AC2+AB2=152+302=1125,
∴15BD=1125.
∴BD=75(cm).
14.解:
∵∠ACO=∠BDO=90°,∠AOC=∠BOD,
∴△ACO∽△BDO,
=,
=
解得AC=60cm.
答:至少要将杠杆A端下压60cm.
15.解:∵AB∥CD,
∴△ABE∽△CDE,
∴==,
∵EF∥AB,
∴△FDE∽△ADB,
∴==,
∵AB=10,
∴EF=6.
答:这棵树的高度为6米.
16.解:设李华由A到A′,身高为A′B′,A′C′代表其影长(如图).
∵AB∥PO,
∴△CBA∽△CPO,
∴,
即,
∴,
同理可得:,
∴,
∴,
当李华从A走到A'的时候,他的影子也从C移到C′,因此速度与路程成正比,
∴,
所以人影顶端在地面上移动的速度为.
故答案为:.
17.解:(1)如图,作垂线或平行线;
(2)如图,作DE⊥AB,CF⊥DE,垂足为E、F,
∵∠A=60°,∠B=∠D=90°,
∴∠BCD=360°﹣∠A﹣∠B﹣∠D=′120°,
在Rt△CDF中,CD=1,∠DCF=∠BCD﹣∠BCF=30°,
DF=,CF=;
∴BE=CF=,AE=AB﹣BE=2﹣;
在Rt△ADE中,∠ADE=90°﹣∠CDF=30°,
∴DE=2﹣,
BC=EF=DE﹣DF=2﹣2,
AD=4﹣.
18.解:图1中,∵△AFD∽△ACB,
∴=,即=,
解得:FD=;
图2中,过点C作CM⊥AB于点M,如图所示:
CM==,设正方形的边长为x,
∵GF∥AB,
∴=,即=,
解得:x=,
∵>,
∴甲同学的设计方案符合要求.
19.解:所作图形如下:
20.解:∵反射角等于入射角,
∴∠BEA=∠DEC.
又∵AB⊥AC,DC⊥AC,
∴∠BAE=∠DCE=90°,
∴△ABE∽△CDE,
∴,
=,
解得AB=m.
答:楼高为m.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
