人教版第二十二章二次函数 22.3实际问题与二次函数尖子生培优练习((word版 带解析))
文档属性
| 名称 | 人教版第二十二章二次函数 22.3实际问题与二次函数尖子生培优练习((word版 带解析)) |  | |
| 格式 | docx | ||
| 文件大小 | 572.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 09:59:15 | ||
图片预览


文档简介
22.3实际问题与二次函数尖子生培优练---2021--2022学年人教版(2012)九年级上学期第二十二章二次函数
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
2.已知学校航模组设计制作的火箭升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1,则下列说法中正确的是( )
A.点火后1s和点火后3s的升空高度相同
B.点火后24s火箭落于地面
C.火箭升空的最大高度为145m
D.点火后10s的升空高度为139m
3.地面竖直向上抛出一小球,小球的高度单位:与小球运动时间单位:之间的函数关系如图所示下列结论:①小球抛出秒时速度为;②小球在空中经过的路程是;③小球的高度时,;④小球抛出秒后,速度越来越快其中正确的是( )
A.①② B.①④ C.①②④ D.②③
4.据省统计局公布的数据,合肥市2021年第一季度GDP总值约为2.4千亿元人民币,若我市第三季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A.
B.
C.
D.
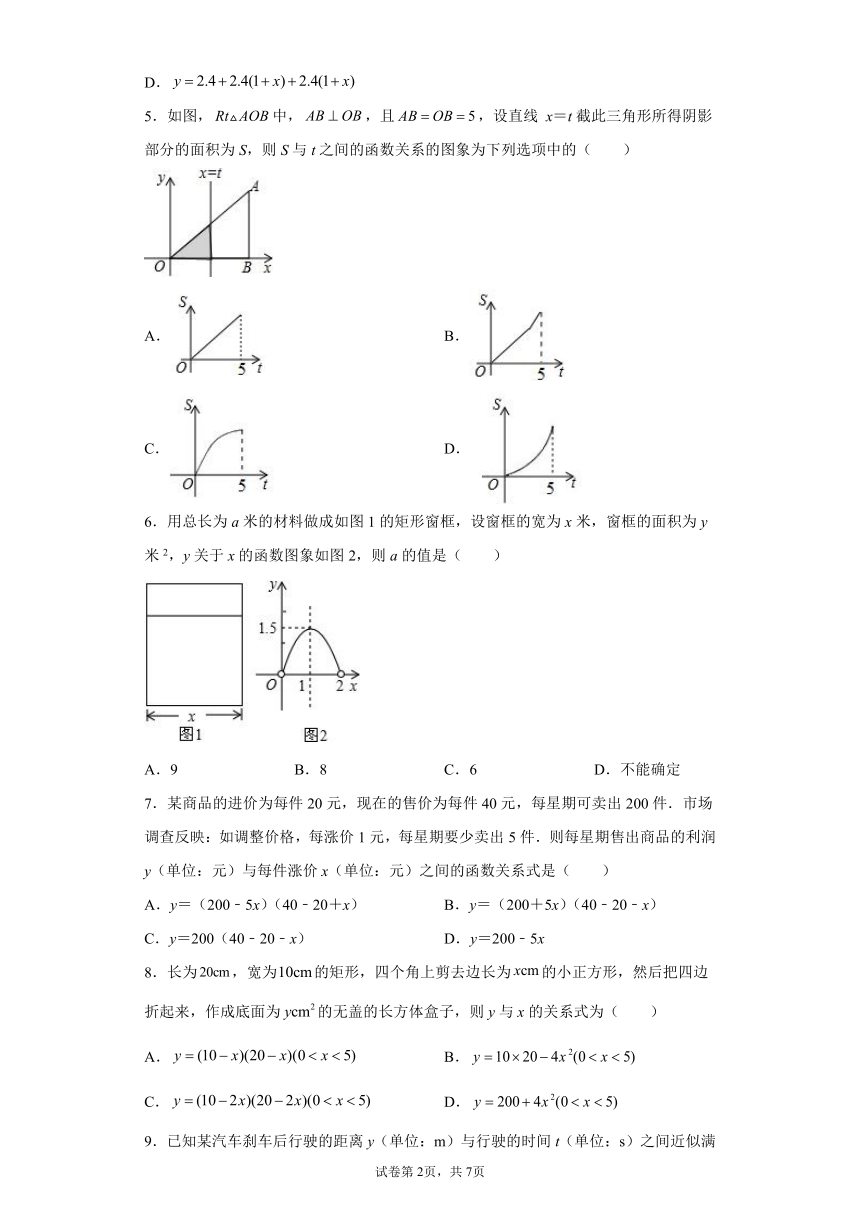
5.如图,中,,且,设直线 x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
A. B.
C. D.
6.用总长为a米的材料做成如图1的矩形窗框,设窗框的宽为x米,窗框的面积为y米2,y关于x的函数图象如图2,则a的值是( )
A.9 B.8 C.6 D.不能确定
7.某商品的进价为每件20元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出5件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=(200﹣5x)(40﹣20+x) B.y=(200+5x)(40﹣20﹣x)
C.y=200(40﹣20﹣x) D.y=200﹣5x
8.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
9.已知某汽车刹车后行驶的距离y(单位:m)与行驶的时间t(单位:s)之间近似满足函数关系y=-6t2+15t,根据上述函数模型和数据,可推断出该汽车刹车后到停下来所用的时间为( )
A.1.25s B.2.25s C.0.25s D.0.75
10.有一块缺角矩形地皮(如图),其中.现准备用此块地建一座地基为长方形(图中用阴影部分表示)的实验大楼,以下四个方案中,地基面积最大的是( )
A. B. C. D.
11.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度超过20m;②足球飞行路线的对称轴是直线t=;③点(9,0)在该抛物线上;④足球被踢出5s~7s时,距离地面的高度逐渐下降.其中正确的结论是( )
A.②③ B.①②③ C.①②③④ D.②③④
12.如图,正方形边长为4,、、、分别是、、、上的点,且.设、两点间的距离为,四边形的面积为,则与的函数图象可能是( )
A. B. C. D.
评卷人得分
二、填空题
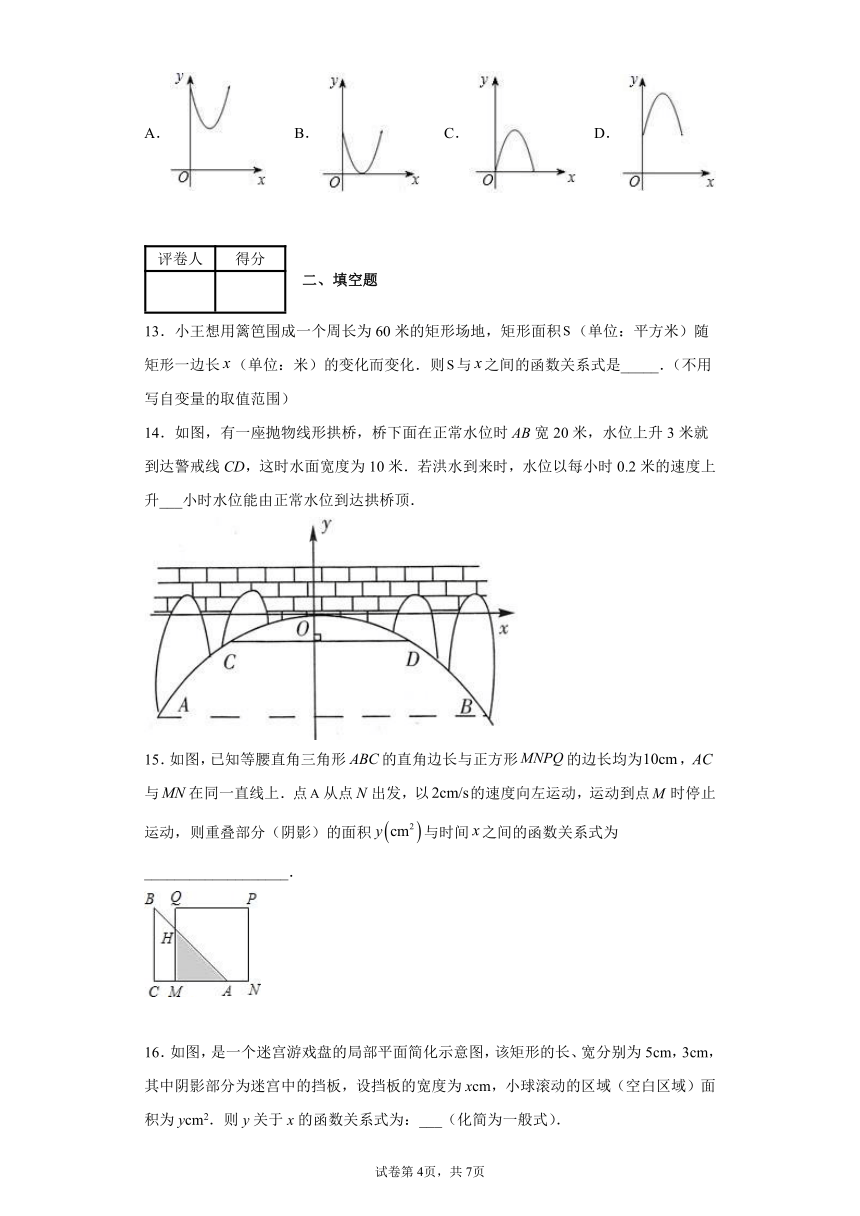
13.小王想用篱笆围成一个周长为60米的矩形场地,矩形面积(单位:平方米)随矩形一边长(单位:米)的变化而变化.则与之间的函数关系式是_____.(不用写自变量的取值范围)
14.如图,有一座抛物线形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就到达警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升___小时水位能由正常水位到达拱桥顶.
15.如图,已知等腰直角三角形的直角边长与正方形的边长均为,与在同一直线上.点从点出发,以的速度向左运动,运动到点时停止运动,则重叠部分(阴影)的面积与时间之间的函数关系式为___________________.
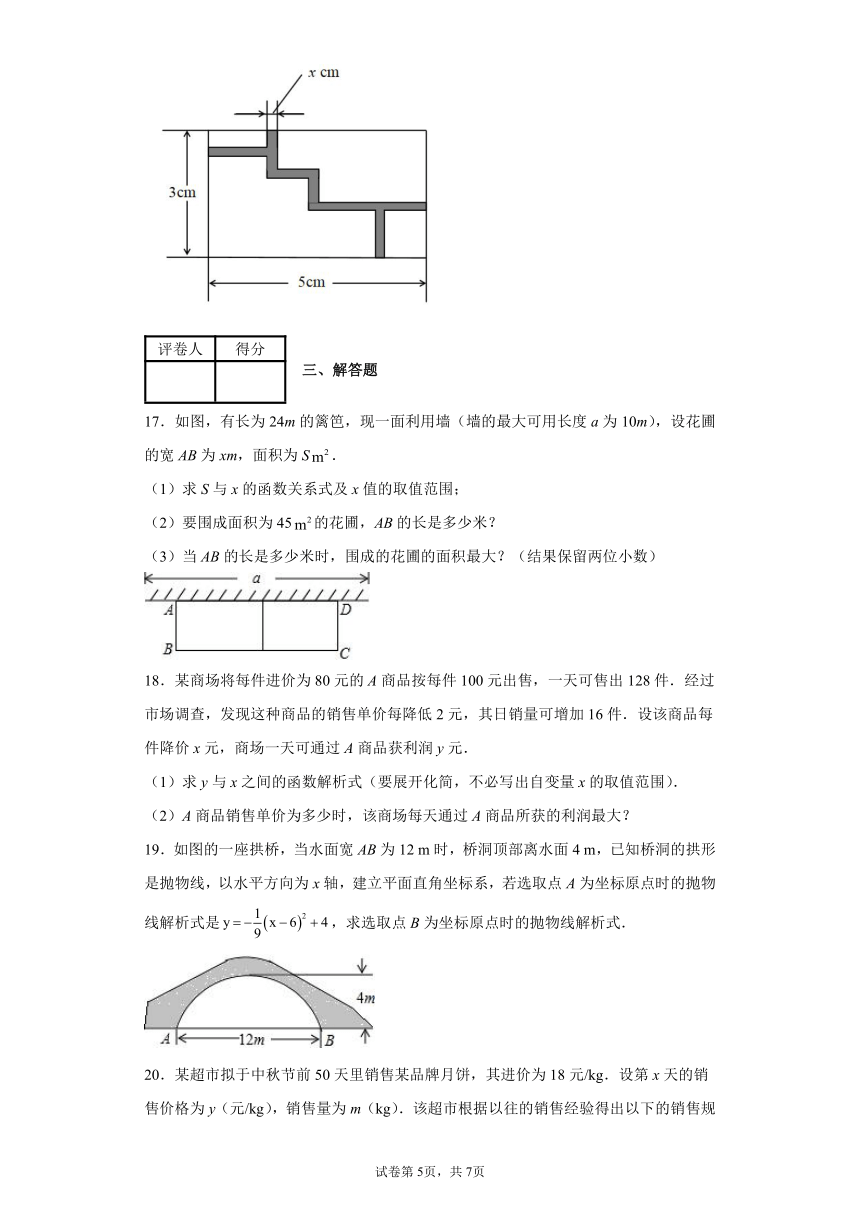
16.如图,是一个迷宫游戏盘的局部平面简化示意图,该矩形的长、宽分别为5cm,3cm,其中阴影部分为迷宫中的挡板,设挡板的宽度为xcm,小球滚动的区域(空白区域)面积为ycm2.则y关于x的函数关系式为:___(化简为一般式).
评卷人得分
三、解答题
17.如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m),设花圃的宽AB为xm,面积为S.
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为45的花圃,AB的长是多少米?
(3)当AB的长是多少米时,围成的花圃的面积最大?(结果保留两位小数)
18.某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低2元,其日销量可增加16件.设该商品每件降价x元,商场一天可通过A商品获利润y元.
(1)求y与x之间的函数解析式(要展开化简,不必写出自变量x的取值范围).
(2)A商品销售单价为多少时,该商场每天通过A商品所获的利润最大?
19.如图的一座拱桥,当水面宽AB为12 m时,桥洞顶部离水面4 m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是,求选取点B为坐标原点时的抛物线解析式.
20.某超市拟于中秋节前50天里销售某品牌月饼,其进价为18元/kg.设第x天的销售价格为y(元/kg),销售量为m(kg).该超市根据以往的销售经验得出以下的销售规律:①当1≤x≤30时,y=40;当3≤x≤50时,y与x满足一次函数关系,且当x=36时,y=37;x=44时,y=33.②m与x的关系为m=5x+50.
(1)当31≤x≤50时,求y与x的关系式;
(2)x为多少时,当天的销售利润w(元)最大?最大利润为多少?
(3)若超市希望第31天到第35天的日销售利润W(元)随x的增大而增大,则需要在当天销售价格的基础上涨a元/kg,求a的最小值.
21.在“乡村振兴”行动中,某村办企业以A,B两种农作物为原料,开发了一种有机产品.A原料的单价是B原料单价的1.5倍.若用900元收购A原料会比用900元收购B原料少100kg,生产该产品每盒需要A原料2kg和B原料4kg,每盒还需其它成本9元.市场调查发现:该产品售价为每盒40元时,每天可卖出150盒.如果每盒的售价每涨1元(售价每盒不能高于45元),那么每天少卖10盒.设每盒涨价x元(x为非负整数),每天销售y盒.
(1)求该产品每盒的成本(成本=原料费+其它成本);
(2)求y与x的函数关系式及自变量x的取值范围;
(3)如何定价才能使每天的利润最大且每天销量较大?每天的最大利润是多少?
22.如图,拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
23.如图,点是y轴正半轴上的点,点A的坐标为,以AC为边作等腰直角三角形ABC,其中,,,以点B为顶点的抛物线经过点A且和x轴交于另一点D,交y轴于点E.
(1)点B的坐标为_____________;
(2)求抛物线的函数表达式;
(3)在第一象限的抛物线上是否存在点P,使得?若存在求点P的坐标,不存在则说明理由.
24.某旅游景点未来15天内,旅游人数y与时间x的关系如下表:每张门票z与时间x之间存在如图所示的一次函数关系(1≤x≤15,且x为整数),请结合上述信息解决下列问题:
时间x(天) 1 4 7 10 …
人数y(人) 320 350 380 410 …
(1)直接写出y关于x的函数关系式.
(2)求z与时间x的函数关系式.
(3)求未来15天中哪一天的门票收入最多,最多是多少?(尽量增加景点的客流量)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
解:由题意得:,
故选B.
2.C
解:A、当t=1时,h=24;当t=3时,h=64;所以点火后1s和点火后3s的升空高度不相同,此选项错误;
B、当t=24时,h=1≠0,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、由h=﹣t2+24t+1=﹣(t-12)2+145知火箭升空的最大高度为145m,此选项正确;
D、当t=10时,h=141m,此选项错误;
故选:C.
3.B
解:①小球抛出秒时达到最高点即速度为;故①正确;
②由图象知小球在空中达到的最大高度是;故②错误;
③设函数解析式为:,
把代入得,解得,
函数解析式为,
把代入解析式得,,
解得:或,
小球的高度时,或,故③错误;
④小球抛出秒后速度越来越快;故④正确;
故选:.
4.C
解:已知平均每个季度增长的百分率为,
则关于的函数表达式是:.
故选:C.
5.D
解:如图示,
∵中,,且,
,
,
,
,
,
,
,
即.
故与之间的函数关系的图象自变量的范围为0≤t≤5、开口向上的二次函数图象;
故选:.
6.C
设窗框的长为,
根据函数图像,可知当时,窗框的面积最大,最大值为,
即
故选C.
7.A
【解】
∵每涨价1元,每星期要少卖出5件,每件涨价x元,
∴销售每件的利润为(40﹣20+x)元,每星期的销售量为(200﹣5x)件,
∴每星期售出商品的利润y=(200﹣5x)(40﹣20+x).
故选:A.
8.C
解:设小正方形边长为xcm,由题意知:
现在底面长为(20-2x)cm,宽为(10-2x)cm,
则y=(10-2x)(20-2x)(0<x<5),
故选:C.
9.A
解:∵y=-6t2+15t= 6(t 1.25)2+9.375,
∴该汽车刹车后到停下来所用的时间为1.25s.
故选A.
10.A
解:如图,作DG⊥AB于G,EF⊥BC于F,DG,EF交于O,设CN=x,
那么∠EDO=∠EDC-90°=45°,
因此△EOD是等腰直角三角形,同理△EQR,△RPD均为等腰直角三角形,
∴EO=OD=AB-CD=20,RP=DP=CN=x,EQ=QR=AM=EO-RP=20-x,AE=BC-OD=60,
如果设阴影部分MRNB的面积为y,
那么y=MR RN=(AE+QR) (CD+RP)=(80-x)(x+90)=7200-10x-x2
因为y是x的开口向下的抛物线,其对称轴为直线x=-5,
所以当x≥0时,二次函数为减函数,
所以此函数的最大值就是当x=0时,y=7200,
故选:A.
11.C解:由题意,抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,
∴h=﹣t2+9t=﹣(t﹣4.5)2+20.25,
∴足球距离地面的最大高度为20.25m>20m,故①正确,
∴抛物线的对称轴t=4.5,故②正确,
∵t=9时,h=0,
∴点(9,0)在该抛物线上,故③正确,
∵当t=5时,h=20,当t=7时,h=14,
∴足球被踢出5s~7s时,距离地面的高度逐渐下降,故④正确.
∴正确的有①②③④,
故选:C.
12.A
解:∵正方形ABCD边长为4,AE=BF=CG=DH
∴AH=BE=CF=DG,∠A=∠B=∠C=∠D
∴△AEH≌△BFE≌△CGF≌△DHG
∴y=4×4-x(4-x)×4
=16-8x+2x2
=2(x-2)2+8
∴y是x的二次函数,函数的顶点坐标为(2,8),开口向上,
从4个选项来看,开口向上的只有A和B,C和D图象开口向下,不符合题意;
但是B的顶点在x轴上,故B不符合题意,只有A符合题意.
故选:A.
13.
【解】
∵矩形周长为60米,一边长米,
∴另一边长为(30-x)米,
∴矩形的面积.
故答案为:.
14.20
解:由题意,设抛物线的解析式为,,,
将,,代入可得:
,解得:,
∴抛物线解析式为:,,
即:正常水位AB距离桥顶4米,
∴(小时),
故答案为:20.
15.
解:∵是等腰直角三角形,
,
∴重叠部分也是等腰直角三角形,
又∵,
∴,
∴,
∴.
故答案为:
16.
【解】
根据题意,将阴影部分平移,如图,
则.
故答案为:.
17.【解】(1)∵四边形ABCD是矩形,四边形ABEF是矩形,四边形EFCD是矩形,
∴AB=CD=EF=x,
∴BC=24-3x,
∴S=AB×BC=x(24-3x)=,
∵24-3x>0, 24-3x≤10,
∴≤x<8,
∴S=,≤x<8;
(2)根据题意,得=45,
解得,
∵≤x<8,
∴舍去,
∴AB=5(米);
(3)∵S=
=,
∴对称轴为直线x=4,
∵≤x<8,且在对称轴右侧y随x的增大而减小,
∴当x=时,S有最大值,
∴S=≈46.67.
即当AB=米时,S的最大值为46.67.
18.解:(1)由题意得,商品每件降价x元时单价为(100﹣x)元,销售量为(128+8x)件,
则y=(128+8x)(100﹣x﹣80)
=﹣8x2+32x+2560,
即y与x之间的函数解析式是y=﹣8x2+32x+2560;
(2)∵y=﹣8x2+32x+2560=﹣8(x﹣2)2+2592,
∴当x=2时,y取得最大值,此时y=2592,
∴销售单价为:100﹣2=98(元),
答:A商品销售单价为98元时,该商场每天通过A商品所获的利润最大.
19.解:如图:
由题意可得出:y=a(x+6)2+4,
将(12,0)代入得出,0=a(12+6)2+4,
解得:,
∴选取点B为坐标原点时的抛物线解析式是:.
故答案为:.
20.解:(1)依题意,当时,;时,,
当时,设,
则有,解得,
与的关系式为:.
(2)依题意,
,
,
整理得,,
当时,
随增大而增大,
时,取最大值,
当时,
,
,
时,取得最大值,此时,
综上所述,为32时,当天的销售利润(元最大,最大利润为4410元.
(3)依题意,
,
第31天到第35天的日销售利润(元随的增大而增大,
对称轴,得,
故的取值范围为.
21.解:(1)设原料单价为元,则原料单价为元,
根据题意,得,
解得: ,
∴,
∴每盒产品的成本为:(元),
答:每盒产品的成本为30元;
(2)∵每盒的售价每涨1元,那么每天少卖10盒.
∴y与x的函数关系式为:,
又∵售价每盒不能高于45元,x为非负整数,
∴自变量x的取值范围为:(x为非负整数);
(3)设每天的利润为w元,
则有:
,
∴w是关于x的一元二次方程,x为非负整数
∴当时,取得最大值为,
∴每盒定价为:42或43(元),
答:定价为42.或43元时才能使每天的利润最大且每天销量较大,每天的最大利润是1560元.
22.解:如图所示,以CD所在直线为x轴,CD的垂直平分线为y轴建立平面直角坐标系,
∵CD=200,
∴抛物线与轴的交点为,,
∴设这条抛物线的解析式为,
∵AB=100,AB与CD的距离为150,
∴点B的坐标为(50,150),
抛物线经过点,
,
解得:,
,
当时,取得最大值,此时,
即拱门的最大高度是200米.
23.【详解】(1)作垂足为F,
∵,
∴∠ACO+∠BCF=90°,∠ACO+∠OAC=90°,
∴∠BCF=∠OAC,
又∵∠AOC=∠CBF=90°,,
∴,
∴,,
∴,所以点B的坐标为;
(2)设抛物线的函数表达式为,
由题意得:,解得:。
所以抛物线的函数表达式为即;
(3)由对称性得,易知,
所以,
设直线AC的表达式为:,
由题意得:,解得,,
所以直线AC的表达式为:;
如图,假设存在点P,设.作轴交AC于Q,则.
所以,,
所以,,
所以,,整理得:,
解得:,
当时,,
此时点P坐标为
当时,,此时点P坐标为
综上所述,AC上方抛物线上存在点P,使得,点P的坐标为或.
24.(1)y=10x+310(1≤x≤15,且x为整数);(2)z=-x+50(1≤x≤15,且x为整数);(3)未来15天中第10天门票最多,最多是16400元
解:(1)由题意可知:y是关于x的一次函数,
∴设y=kx+b,
将(1,320)、(4,350)代入,
得,
解得,
∴y关于x的函数关系式为y=10x+310(1≤x≤15,且x为整数);
(2)设z=mx+n,
将点(1,49)、(15,35)代入,
得,
解得,
∴z与时间x的函数关系式为z=﹣x+50(1≤x≤15,且x为整数);
(3)设第x天的门票收入为w,
则w=yz
=(10x+310)(﹣x+50)
=﹣10x2﹣310x+500x+15500
=﹣10x2+190x+15500,
∵﹣10<0,
∴w有最大值,
∵对称轴为直线,10-9.5=9.5-9=0.5,
当x=10或9时,w取得最大值,最大值为16400,
又∵10>9,
∴未来15天中第10天的门票收入最多,最多是16400元.
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
2.已知学校航模组设计制作的火箭升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1,则下列说法中正确的是( )
A.点火后1s和点火后3s的升空高度相同
B.点火后24s火箭落于地面
C.火箭升空的最大高度为145m
D.点火后10s的升空高度为139m
3.地面竖直向上抛出一小球,小球的高度单位:与小球运动时间单位:之间的函数关系如图所示下列结论:①小球抛出秒时速度为;②小球在空中经过的路程是;③小球的高度时,;④小球抛出秒后,速度越来越快其中正确的是( )
A.①② B.①④ C.①②④ D.②③
4.据省统计局公布的数据,合肥市2021年第一季度GDP总值约为2.4千亿元人民币,若我市第三季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A.
B.
C.
D.
5.如图,中,,且,设直线 x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
A. B.
C. D.
6.用总长为a米的材料做成如图1的矩形窗框,设窗框的宽为x米,窗框的面积为y米2,y关于x的函数图象如图2,则a的值是( )
A.9 B.8 C.6 D.不能确定
7.某商品的进价为每件20元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出5件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=(200﹣5x)(40﹣20+x) B.y=(200+5x)(40﹣20﹣x)
C.y=200(40﹣20﹣x) D.y=200﹣5x
8.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
9.已知某汽车刹车后行驶的距离y(单位:m)与行驶的时间t(单位:s)之间近似满足函数关系y=-6t2+15t,根据上述函数模型和数据,可推断出该汽车刹车后到停下来所用的时间为( )
A.1.25s B.2.25s C.0.25s D.0.75
10.有一块缺角矩形地皮(如图),其中.现准备用此块地建一座地基为长方形(图中用阴影部分表示)的实验大楼,以下四个方案中,地基面积最大的是( )
A. B. C. D.
11.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度超过20m;②足球飞行路线的对称轴是直线t=;③点(9,0)在该抛物线上;④足球被踢出5s~7s时,距离地面的高度逐渐下降.其中正确的结论是( )
A.②③ B.①②③ C.①②③④ D.②③④
12.如图,正方形边长为4,、、、分别是、、、上的点,且.设、两点间的距离为,四边形的面积为,则与的函数图象可能是( )
A. B. C. D.
评卷人得分
二、填空题
13.小王想用篱笆围成一个周长为60米的矩形场地,矩形面积(单位:平方米)随矩形一边长(单位:米)的变化而变化.则与之间的函数关系式是_____.(不用写自变量的取值范围)
14.如图,有一座抛物线形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就到达警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升___小时水位能由正常水位到达拱桥顶.
15.如图,已知等腰直角三角形的直角边长与正方形的边长均为,与在同一直线上.点从点出发,以的速度向左运动,运动到点时停止运动,则重叠部分(阴影)的面积与时间之间的函数关系式为___________________.
16.如图,是一个迷宫游戏盘的局部平面简化示意图,该矩形的长、宽分别为5cm,3cm,其中阴影部分为迷宫中的挡板,设挡板的宽度为xcm,小球滚动的区域(空白区域)面积为ycm2.则y关于x的函数关系式为:___(化简为一般式).
评卷人得分
三、解答题
17.如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m),设花圃的宽AB为xm,面积为S.
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为45的花圃,AB的长是多少米?
(3)当AB的长是多少米时,围成的花圃的面积最大?(结果保留两位小数)
18.某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低2元,其日销量可增加16件.设该商品每件降价x元,商场一天可通过A商品获利润y元.
(1)求y与x之间的函数解析式(要展开化简,不必写出自变量x的取值范围).
(2)A商品销售单价为多少时,该商场每天通过A商品所获的利润最大?
19.如图的一座拱桥,当水面宽AB为12 m时,桥洞顶部离水面4 m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是,求选取点B为坐标原点时的抛物线解析式.
20.某超市拟于中秋节前50天里销售某品牌月饼,其进价为18元/kg.设第x天的销售价格为y(元/kg),销售量为m(kg).该超市根据以往的销售经验得出以下的销售规律:①当1≤x≤30时,y=40;当3≤x≤50时,y与x满足一次函数关系,且当x=36时,y=37;x=44时,y=33.②m与x的关系为m=5x+50.
(1)当31≤x≤50时,求y与x的关系式;
(2)x为多少时,当天的销售利润w(元)最大?最大利润为多少?
(3)若超市希望第31天到第35天的日销售利润W(元)随x的增大而增大,则需要在当天销售价格的基础上涨a元/kg,求a的最小值.
21.在“乡村振兴”行动中,某村办企业以A,B两种农作物为原料,开发了一种有机产品.A原料的单价是B原料单价的1.5倍.若用900元收购A原料会比用900元收购B原料少100kg,生产该产品每盒需要A原料2kg和B原料4kg,每盒还需其它成本9元.市场调查发现:该产品售价为每盒40元时,每天可卖出150盒.如果每盒的售价每涨1元(售价每盒不能高于45元),那么每天少卖10盒.设每盒涨价x元(x为非负整数),每天销售y盒.
(1)求该产品每盒的成本(成本=原料费+其它成本);
(2)求y与x的函数关系式及自变量x的取值范围;
(3)如何定价才能使每天的利润最大且每天销量较大?每天的最大利润是多少?
22.如图,拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
23.如图,点是y轴正半轴上的点,点A的坐标为,以AC为边作等腰直角三角形ABC,其中,,,以点B为顶点的抛物线经过点A且和x轴交于另一点D,交y轴于点E.
(1)点B的坐标为_____________;
(2)求抛物线的函数表达式;
(3)在第一象限的抛物线上是否存在点P,使得?若存在求点P的坐标,不存在则说明理由.
24.某旅游景点未来15天内,旅游人数y与时间x的关系如下表:每张门票z与时间x之间存在如图所示的一次函数关系(1≤x≤15,且x为整数),请结合上述信息解决下列问题:
时间x(天) 1 4 7 10 …
人数y(人) 320 350 380 410 …
(1)直接写出y关于x的函数关系式.
(2)求z与时间x的函数关系式.
(3)求未来15天中哪一天的门票收入最多,最多是多少?(尽量增加景点的客流量)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
解:由题意得:,
故选B.
2.C
解:A、当t=1时,h=24;当t=3时,h=64;所以点火后1s和点火后3s的升空高度不相同,此选项错误;
B、当t=24时,h=1≠0,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、由h=﹣t2+24t+1=﹣(t-12)2+145知火箭升空的最大高度为145m,此选项正确;
D、当t=10时,h=141m,此选项错误;
故选:C.
3.B
解:①小球抛出秒时达到最高点即速度为;故①正确;
②由图象知小球在空中达到的最大高度是;故②错误;
③设函数解析式为:,
把代入得,解得,
函数解析式为,
把代入解析式得,,
解得:或,
小球的高度时,或,故③错误;
④小球抛出秒后速度越来越快;故④正确;
故选:.
4.C
解:已知平均每个季度增长的百分率为,
则关于的函数表达式是:.
故选:C.
5.D
解:如图示,
∵中,,且,
,
,
,
,
,
,
,
即.
故与之间的函数关系的图象自变量的范围为0≤t≤5、开口向上的二次函数图象;
故选:.
6.C
设窗框的长为,
根据函数图像,可知当时,窗框的面积最大,最大值为,
即
故选C.
7.A
【解】
∵每涨价1元,每星期要少卖出5件,每件涨价x元,
∴销售每件的利润为(40﹣20+x)元,每星期的销售量为(200﹣5x)件,
∴每星期售出商品的利润y=(200﹣5x)(40﹣20+x).
故选:A.
8.C
解:设小正方形边长为xcm,由题意知:
现在底面长为(20-2x)cm,宽为(10-2x)cm,
则y=(10-2x)(20-2x)(0<x<5),
故选:C.
9.A
解:∵y=-6t2+15t= 6(t 1.25)2+9.375,
∴该汽车刹车后到停下来所用的时间为1.25s.
故选A.
10.A
解:如图,作DG⊥AB于G,EF⊥BC于F,DG,EF交于O,设CN=x,
那么∠EDO=∠EDC-90°=45°,
因此△EOD是等腰直角三角形,同理△EQR,△RPD均为等腰直角三角形,
∴EO=OD=AB-CD=20,RP=DP=CN=x,EQ=QR=AM=EO-RP=20-x,AE=BC-OD=60,
如果设阴影部分MRNB的面积为y,
那么y=MR RN=(AE+QR) (CD+RP)=(80-x)(x+90)=7200-10x-x2
因为y是x的开口向下的抛物线,其对称轴为直线x=-5,
所以当x≥0时,二次函数为减函数,
所以此函数的最大值就是当x=0时,y=7200,
故选:A.
11.C解:由题意,抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,
∴h=﹣t2+9t=﹣(t﹣4.5)2+20.25,
∴足球距离地面的最大高度为20.25m>20m,故①正确,
∴抛物线的对称轴t=4.5,故②正确,
∵t=9时,h=0,
∴点(9,0)在该抛物线上,故③正确,
∵当t=5时,h=20,当t=7时,h=14,
∴足球被踢出5s~7s时,距离地面的高度逐渐下降,故④正确.
∴正确的有①②③④,
故选:C.
12.A
解:∵正方形ABCD边长为4,AE=BF=CG=DH
∴AH=BE=CF=DG,∠A=∠B=∠C=∠D
∴△AEH≌△BFE≌△CGF≌△DHG
∴y=4×4-x(4-x)×4
=16-8x+2x2
=2(x-2)2+8
∴y是x的二次函数,函数的顶点坐标为(2,8),开口向上,
从4个选项来看,开口向上的只有A和B,C和D图象开口向下,不符合题意;
但是B的顶点在x轴上,故B不符合题意,只有A符合题意.
故选:A.
13.
【解】
∵矩形周长为60米,一边长米,
∴另一边长为(30-x)米,
∴矩形的面积.
故答案为:.
14.20
解:由题意,设抛物线的解析式为,,,
将,,代入可得:
,解得:,
∴抛物线解析式为:,,
即:正常水位AB距离桥顶4米,
∴(小时),
故答案为:20.
15.
解:∵是等腰直角三角形,
,
∴重叠部分也是等腰直角三角形,
又∵,
∴,
∴,
∴.
故答案为:
16.
【解】
根据题意,将阴影部分平移,如图,
则.
故答案为:.
17.【解】(1)∵四边形ABCD是矩形,四边形ABEF是矩形,四边形EFCD是矩形,
∴AB=CD=EF=x,
∴BC=24-3x,
∴S=AB×BC=x(24-3x)=,
∵24-3x>0, 24-3x≤10,
∴≤x<8,
∴S=,≤x<8;
(2)根据题意,得=45,
解得,
∵≤x<8,
∴舍去,
∴AB=5(米);
(3)∵S=
=,
∴对称轴为直线x=4,
∵≤x<8,且在对称轴右侧y随x的增大而减小,
∴当x=时,S有最大值,
∴S=≈46.67.
即当AB=米时,S的最大值为46.67.
18.解:(1)由题意得,商品每件降价x元时单价为(100﹣x)元,销售量为(128+8x)件,
则y=(128+8x)(100﹣x﹣80)
=﹣8x2+32x+2560,
即y与x之间的函数解析式是y=﹣8x2+32x+2560;
(2)∵y=﹣8x2+32x+2560=﹣8(x﹣2)2+2592,
∴当x=2时,y取得最大值,此时y=2592,
∴销售单价为:100﹣2=98(元),
答:A商品销售单价为98元时,该商场每天通过A商品所获的利润最大.
19.解:如图:
由题意可得出:y=a(x+6)2+4,
将(12,0)代入得出,0=a(12+6)2+4,
解得:,
∴选取点B为坐标原点时的抛物线解析式是:.
故答案为:.
20.解:(1)依题意,当时,;时,,
当时,设,
则有,解得,
与的关系式为:.
(2)依题意,
,
,
整理得,,
当时,
随增大而增大,
时,取最大值,
当时,
,
,
时,取得最大值,此时,
综上所述,为32时,当天的销售利润(元最大,最大利润为4410元.
(3)依题意,
,
第31天到第35天的日销售利润(元随的增大而增大,
对称轴,得,
故的取值范围为.
21.解:(1)设原料单价为元,则原料单价为元,
根据题意,得,
解得: ,
∴,
∴每盒产品的成本为:(元),
答:每盒产品的成本为30元;
(2)∵每盒的售价每涨1元,那么每天少卖10盒.
∴y与x的函数关系式为:,
又∵售价每盒不能高于45元,x为非负整数,
∴自变量x的取值范围为:(x为非负整数);
(3)设每天的利润为w元,
则有:
,
∴w是关于x的一元二次方程,x为非负整数
∴当时,取得最大值为,
∴每盒定价为:42或43(元),
答:定价为42.或43元时才能使每天的利润最大且每天销量较大,每天的最大利润是1560元.
22.解:如图所示,以CD所在直线为x轴,CD的垂直平分线为y轴建立平面直角坐标系,
∵CD=200,
∴抛物线与轴的交点为,,
∴设这条抛物线的解析式为,
∵AB=100,AB与CD的距离为150,
∴点B的坐标为(50,150),
抛物线经过点,
,
解得:,
,
当时,取得最大值,此时,
即拱门的最大高度是200米.
23.【详解】(1)作垂足为F,
∵,
∴∠ACO+∠BCF=90°,∠ACO+∠OAC=90°,
∴∠BCF=∠OAC,
又∵∠AOC=∠CBF=90°,,
∴,
∴,,
∴,所以点B的坐标为;
(2)设抛物线的函数表达式为,
由题意得:,解得:。
所以抛物线的函数表达式为即;
(3)由对称性得,易知,
所以,
设直线AC的表达式为:,
由题意得:,解得,,
所以直线AC的表达式为:;
如图,假设存在点P,设.作轴交AC于Q,则.
所以,,
所以,,
所以,,整理得:,
解得:,
当时,,
此时点P坐标为
当时,,此时点P坐标为
综上所述,AC上方抛物线上存在点P,使得,点P的坐标为或.
24.(1)y=10x+310(1≤x≤15,且x为整数);(2)z=-x+50(1≤x≤15,且x为整数);(3)未来15天中第10天门票最多,最多是16400元
解:(1)由题意可知:y是关于x的一次函数,
∴设y=kx+b,
将(1,320)、(4,350)代入,
得,
解得,
∴y关于x的函数关系式为y=10x+310(1≤x≤15,且x为整数);
(2)设z=mx+n,
将点(1,49)、(15,35)代入,
得,
解得,
∴z与时间x的函数关系式为z=﹣x+50(1≤x≤15,且x为整数);
(3)设第x天的门票收入为w,
则w=yz
=(10x+310)(﹣x+50)
=﹣10x2﹣310x+500x+15500
=﹣10x2+190x+15500,
∵﹣10<0,
∴w有最大值,
∵对称轴为直线,10-9.5=9.5-9=0.5,
当x=10或9时,w取得最大值,最大值为16400,
又∵10>9,
∴未来15天中第10天的门票收入最多,最多是16400元.
同课章节目录
