北师大版九年级数学上册第四章相似图形培优试题(Word版,附答案)
文档属性
| 名称 | 北师大版九年级数学上册第四章相似图形培优试题(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 964.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 22:03:58 | ||
图片预览



文档简介
相似图形培优试题
一、选择题
1、已知:如图, ,BD: :5,那么下列结论正确的是( )
A. B. C. D.
2、如图,一人站在两等高的路灯之间走动, 为人 在路灯 照射下的影子, 为人 在路灯 照射下的影子.当人从点 走向点 时两段影子之和 的变化趋势是( )
A. 先变长后变短 B. 先变短后变长 C. 不变 D. 先变短后变长再变短
3、如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠ B.AD=1,AC=2,△ADC的面积为S,则△BCD的面积为( )
A. S B. 2S C. 3S D. 4S
4、如图,在 中,点 , , 分别在边 , , 上,且 , .若 ,则 的值为( ).
A. B. C. D.
5、如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的周长之比为1:2,点C的坐标为(﹣2,0),若点B的坐标为(﹣5,1),则点D的坐标为( )
A. (4,﹣2) B. (6,﹣2) C. (8,﹣2) D. (10,﹣2)
6、在 中,如果各边长度都扩大为原来的2倍,那么锐角 的余弦值( )
A. 扩大2倍 B. 缩小2倍 C. 扩大4倍 D. 没有变化
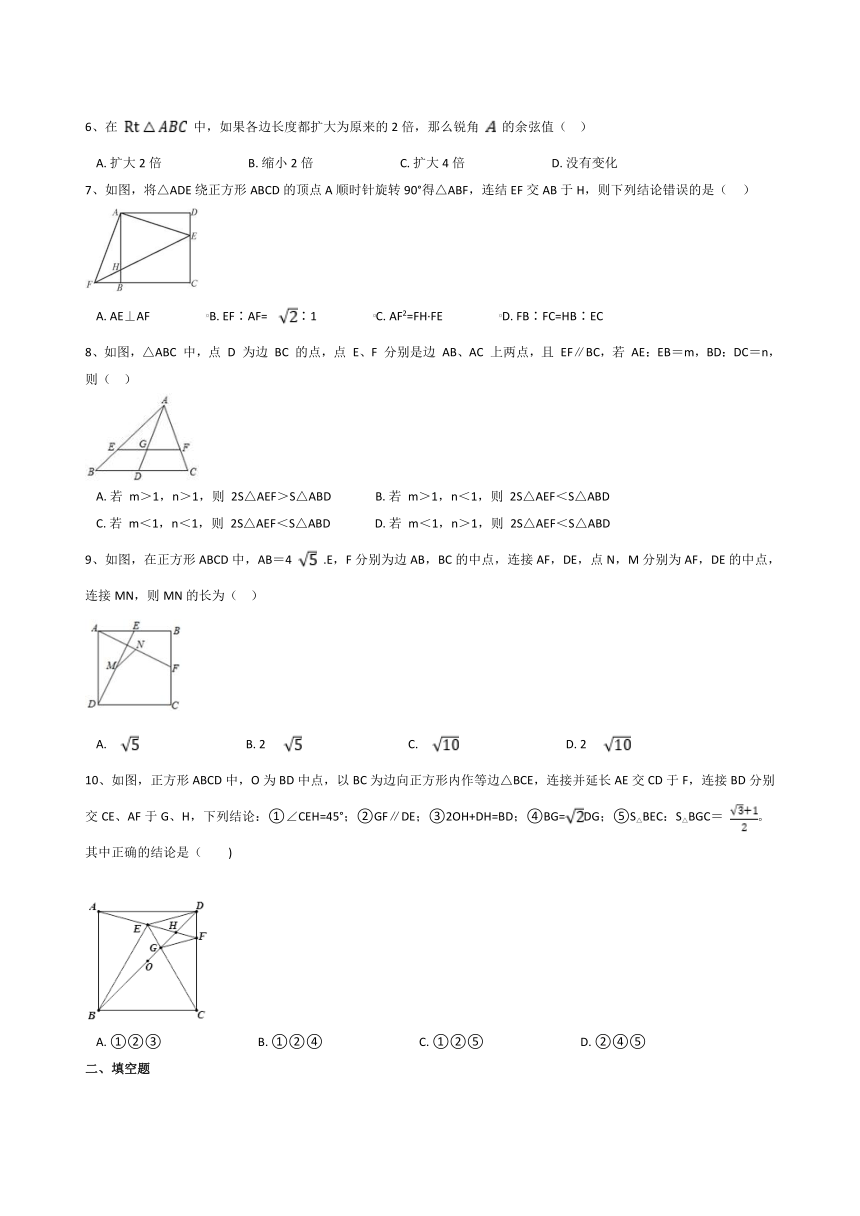
7、如图,将△ADE绕正方形ABCD的顶点A顺时针旋转90°得△ABF,连结EF交AB于H,则下列结论错误的是( )
A. AE⊥AF B. EF∶AF=∶1 C. AF2=FH·FE D. FB∶FC=HB∶EC
8、如图,△ABC 中,点 D 为边 BC 的点,点 E、F 分别是边 AB、AC 上两点,且 EF∥BC,若 AE:EB=m,BD:DC=n,则( )
A. 若 m>1,n>1,则 2S△AEF>S△ABD B. 若 m>1,n<1,则 2S△AEF<S△ABD
C. 若 m<1,n<1,则 2S△AEF<S△ABD D. 若 m<1,n>1,则 2S△AEF<S△ABD
9、如图,在正方形ABCD中,AB=4 .E,F分别为边AB,BC的中点,连接AF,DE,点N,M分别为AF,DE的中点,连接MN,则MN的长为( )
A. B. 2 C. D. 2
10、如图,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接并延长AE交CD于F,连接BD分别交CE、AF于G、H,下列结论:①∠CEH=45°;②GF∥DE;③2OH+DH=BD;④BG=DG;⑤S△BEC:S△BGC= 。其中正确的结论是( )
A. ①②③ B. ①②④ C. ①②⑤ D. ②④⑤
二、填空题
1、已知线段a=3,b=27,则a,b的比例中项线段长等于________.
2、如图是用卡钳测量容器内径的示意图,现量得卡钳上 , 两个端点之间的距离为 , ,则容器的内径是________.
3、在平面直角坐标中,△ABC的顶点坐标分别是A(1,1),B(4,2),C(3,5),以点A为位似中心,相似比为1:把三角形ABC缩小,得到△AB1C1 , 则点C的对应点C1的坐标为 .
4、如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则 的值为 .
5、如图,已知正方形ABCD的边长为1,点M是BC边上的动点(不与B,C重合),点N是AM的中点,过点N作EF⊥AM,分别交AB,BD,CD于点E,K,F,设BM=x.
( 1 )AE的长为________(用含x的代数式表示);
( 2 )设EK=2KF,则 的值为________.
6、如图,在矩形ABCD中,AD= AB , ∠BAD的平分线交BC于点E , DH⊥AE于点H , 连接BH并延长交CD于点F , 连接DE交BF于点O , 下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF , 其中正确的有________.
三、解答题
1、如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积.
2、如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3 , AF=2 , 求AE的长.
3、如图,为了测量一栋楼的高度 ,小明同学先在操场上 处放一面镜子,向后退到 处,恰好在镜子中看到楼的顶部 ;再将镜子放到 处,然后后退到 处,恰好再次在镜子中看到楼的顶部 ( 在同一条直线上).测得 , ,如果小明眼睛距地面高度 为 ,试确定楼的高度 .
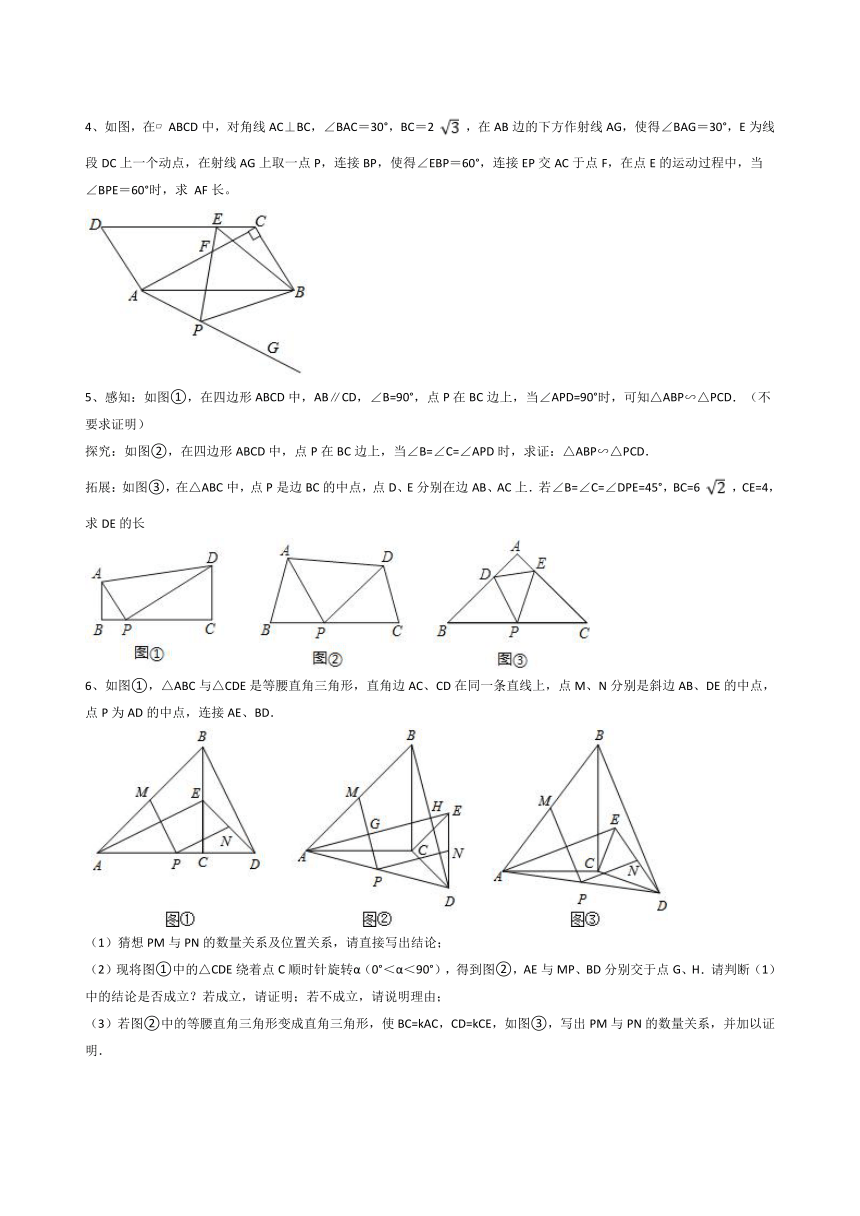
4、如图,在 ABCD中,对角线AC⊥BC,∠BAC=30°,BC=2 ,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,求 AF长。
5、感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6 ,CE=4,求DE的长
6、如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.
7、已知:Rt△A′BC′≌Rt△ABC,∠A′C′B=∠ACB=90°,∠A′BC′=∠ABC=60°,Rt△A′BC′可绕点B旋转,设旋转过程中直线CC′和AA′相交于点D.
(1)如图1所示,当点C′在AB边上时,判断线段AD和线段A′D之间的数量关系,并证明你的结论;
(2)将Rt△A′BC′由图1的位置旋转到图2的位置时,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)将Rt△A′BC′由图1的位置按顺时针方向旋转α角(0°≤α≤120°),当A、C′、A′三点在一条直线上时,请直接写出旋转角的度数.
8、如图 ,在 中, , ,点D是AC的中点,连接BD,过点C作CE平分 交BD于点E,点F在AB上,且
(1)求证: ;
(2)如图②,过点A作 交BD的延长线于点G,
①若 ,求CF; ②设CF交BD于H,求 的值.
9、如图
(1)如图1,在△ABC中,AB>AC,点D,E分别在边AB,AC上,且DE∥BC,若AD=2,AE= ,则 的值是________;
(2)如图2,在(1)的条件下,将△ADE绕点A逆时针方向旋转一定的角度,连接CE和BD, 的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
(3)如图3,在四边形ABCD中,AC⊥BC于点C,∠BAC=∠ADC=θ,且tanθ= ,当CD=6,AD=3时,请直接写出线段BD的长度.
答案解析部分
一、单选题
1. C 2. C 3.C 4.A 5.A 6.D 7.C 8.D 9.C 10.C
二、填空题
1.9 2. 15cm 3. (2,3)或(0,-1) 4. 5. ;x 6. ①②③④
三、解答题
1.【答案】 解答:由已知得,DG∥BC∴△ADG∽△ABC,∵AH⊥BC∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m)= ,即DG= =50(m),∴S矩形DEFG=DE×DG=2000(m2).
2.【答案】 证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠B+∠C=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC;
(2)解:∵四边形ABCD是平行四边形,
∴CD=AB=4,
由(1)知△ADF∽△DEC,
∴ ,
∴DE= .
在Rt△ADE中,由勾股定理得:AE= .
3.【答案】 解:设 关于点 的对称点为 ,由光的反射定律知,延长 相交于 ,
连接 并延长交 于 ,
∥ , ∽ ,
,
即 ,
,
.
答:楼的高度 为32米。
4.【答案】 解:如图,连接PC交AB于T,作PN⊥AB于N,CM⊥PC交PE的延长线于M.
∵AC⊥BC,
∴∠ACB=90°,
∵BC= ,∠BAC=30°,
∴AB=2BC= ,AC= BC=6,∠ABC=60°,
∵∠EPB=∠EBP=60°,
∴△EPB是等边三角形,
∴∠PEB=60°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BCE=180°﹣∠ABC=120°,
∴∠EPB+∠BCE=180°,
∴P,B,C,E四点共圆,
∴∠PCB=∠PEB=60°,∠MPC=∠EBC,
∵∠TCB=∠CBT=60°
∴△TCB是等边三角形,
∴∠BCT=60°,∠ACT=30°,BT=BC=AT= ,
∵∠BAG=∠BAC=30°,
∴∠APC=90°,
∴PA=AT cos30°=3,AN=PA cos30°= ,PN= PA= ,PC= PA= ,
∴BN=AB﹣AN= ,
∵∠PBE=∠CBT=60°,
∴∠PBN=∠CBE=∠CPM,
∵∠PCM=∠PNB=90°,
∴△PCM∽△BNP,
∴ ,
∴ ,
∴CM= ,
∵PA⊥PC,CM⊥PC,
∴CM∥PA,
∴ ,
∴AF= AC= .
故答案为 .
5.【答案】 解:感知:∵∠APD=90°,
∴∠APB+∠DPC=90°,
∵∠B=90°,
∴∠APB+∠BAP=90°,
∴∠BAP=∠DPC,
∵AB∥CD,∠B=90°,
∴∠C=∠B=90°,
∴△ABP∽△DCP.
探究:∵∠APC=∠BAP+∠B,∠APC=∠APD+∠CPD,
∴∠BAP+∠B=∠APD+∠CPD.
∵∠B=∠APD,
∴∠BAP=∠CPD.
∵∠B=∠C,
∴△ABP∽△PCD,
拓展:同探究的方法得出,△BDP∽△CPE,
∴ ,
∵点P是边BC的中点,
∴BP=CP=3 ,
∵CE=4,
∴ ,
∴BD= ,
∵∠B=∠C=45°,
∴∠A=180°﹣∠B﹣∠C=90°,
即AC⊥AB且AC=AB=6,
∴AD=AB﹣BD=6﹣ = ,AE=AC﹣CE=6﹣4=2,
在Rt△ADE中,DE= .
6.【答案】 (1)解:PM=PN,PM⊥PN,理由如下:
∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中
,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠EAC=∠CBD,
∵点M、N分别是斜边AB、DE的中点,点P为AD的中点,
∴PM= BD,PN= AE,
∴PM=PN,
∵PM∥BD,PN∥AE,AE⊥BD,
∴∠NPD=∠EAC,∠MPA=∠BDC,∠EAC+∠BDC=90°,
∴∠MPA+∠NPC=90°,
∴∠MPN=90°,
即PM⊥PN.
(2)解:∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,
∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD.
∴△ACE≌△BCD.
∴AE=BD,∠CAE=∠CBD.
又∵∠AOC=∠BOE,
∠CAE=∠CBD,
∴∠BHO=∠ACO=90°.
∵点P、M、N分别为AD、AB、DE的中点,
∴PM= BD,PM∥BD;
PN= AE,PN∥AE.
∴PM=PN.
∴∠MGE+∠BHA=180°.
∴∠MGE=90°.
∴∠MPN=90°.
∴PM⊥PN
(3)解:PM=kPN
∵△ACB和△ECD是直角三角形,
∴∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD.
∵BC=kAC,CD=kCE,
∴ =k.
∴△BCD∽△ACE.
∴BD=kAE.
∵点P、M、N分别为AD、AB、DE的中点,
∴PM= BD,PN= AE.
∴PM=kPN.
7.【答案】 答:(1)AD=A′D.证明:如图1,∵Rt△A′BC′≌Rt△ABC,∴BC=BC′,BA=BA′.∵∠A′BC′=∠ABC=60°,∴△BCC′和△BAA′都是等边三角形.∴∠BAA′=∠BC′C=60°.∵∠A′C′B=90°,∴∠DC′A′=30°.∵∠AC′D=∠BC′C=60°,∴∠ADC′=60°.∴∠DA′C′=30°.∴∠DAC′=∠DC′A,∠DC′A′=∠DA′C′.∴AD=DC′,DC′=DA′.∴AD=A′D.(2)仍然成立:AD=A′D.证法一:利用相似.如图2﹣1.由旋转可得,BA=BA′,BC=BC′,∠CBC′=∠ABA′∵∠1=(180°﹣∠ABA′),∠3=(180°﹣∠CBC′)∴∠1=∠3.设AB、CD交于点O,则∠AOD=∠BOC∴△BOC∽△DOA.∴∠2=∠4,= . 连接BD,∵∠BOD=∠COA,∴△BOD∽△COA.∴∠5=∠6.∵∠ACB=90°,∴∠2+∠5=90°.∴∠4+∠6=90°,即∠ADB=90°.∵BA=BA′,∠ADB=90°,∴AD=A′D.证法二:利用全等.如图2﹣2.过点A作AE∥A′C′,交CD的延长线于点E,则∠1=∠2,∠E=∠3.由旋转可得,AC=A′C′,BC=BC′,∴∠4=∠5.∵∠ACB=∠A′C′B=90°,∴∠5+∠6=∠3+∠4=90°,∴∠3=∠6.∴∠E=∠6,∴AE=AC=A′C′.在△ADE与△A′DC′中,∴△ADE≌△A′DC′(ASA),∴AD=A′D.(3)当A、C′、A′三点在一条直线上时,如图3,则有∠AC′B=180°﹣∠A′C′B=90°.在Rt△ACB和Rt△AC′B中, . ∴Rt△ACB≌Rt△AC′B (HL).∴∠ABC=∠ABC′=60°.∴当A、C′、A′三点在一条直线上时,旋转角α的度数为60°.
8.【答案】 (1)解:如图①, , ,
,
平分 ,
,
,
在 和 中,
≌ ,
;
(2)解:①如图②,延长CE,交AB于点M,
,CM平分 ,
是AB的中点, ,
,
,即 ,
, ,
, ,
≌ ,
,
,
②由①可知, , ,
设 ,则 ,所以 ,所以 ,
由勾股定理得: ,
,
,
, ,
,
∽ ,
.
9.【答案】 (1)
(2)解: 的值不变化,值为 ;理由如下:
由(1)得:DE∥BC,
∴△ADE∽△ABC,
∴ = ,
由旋转的性质得:∠BAD=∠CAE,
∴△ABD∽△ACE,
∴ = =
(3)解:作AE⊥CD于E,DM⊥AC于M,DN⊥BC于N,如图3所示:
则四边形DMCN是矩形,
∴DM=CN,DN=MC,
∵∠BAC=∠ADC=θ,且tanθ= ,
∴ = , = ,
∴ = ,
∴AE= AD= ×3= ,DE= AE= ,
∴CE=CD﹣DE=6﹣ = ,
∴AC= = =
∴BC= AC= ,
∵△ACD的面积= AC×DM= CD×AE,
∴CN=DM= = ,
∴BN=BC+CN= ,AM= = = ,
∴DN=MC=AM+AC=
∴BD= = =
一、选择题
1、已知:如图, ,BD: :5,那么下列结论正确的是( )
A. B. C. D.
2、如图,一人站在两等高的路灯之间走动, 为人 在路灯 照射下的影子, 为人 在路灯 照射下的影子.当人从点 走向点 时两段影子之和 的变化趋势是( )
A. 先变长后变短 B. 先变短后变长 C. 不变 D. 先变短后变长再变短
3、如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠ B.AD=1,AC=2,△ADC的面积为S,则△BCD的面积为( )
A. S B. 2S C. 3S D. 4S
4、如图,在 中,点 , , 分别在边 , , 上,且 , .若 ,则 的值为( ).
A. B. C. D.
5、如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的周长之比为1:2,点C的坐标为(﹣2,0),若点B的坐标为(﹣5,1),则点D的坐标为( )
A. (4,﹣2) B. (6,﹣2) C. (8,﹣2) D. (10,﹣2)
6、在 中,如果各边长度都扩大为原来的2倍,那么锐角 的余弦值( )
A. 扩大2倍 B. 缩小2倍 C. 扩大4倍 D. 没有变化
7、如图,将△ADE绕正方形ABCD的顶点A顺时针旋转90°得△ABF,连结EF交AB于H,则下列结论错误的是( )
A. AE⊥AF B. EF∶AF=∶1 C. AF2=FH·FE D. FB∶FC=HB∶EC
8、如图,△ABC 中,点 D 为边 BC 的点,点 E、F 分别是边 AB、AC 上两点,且 EF∥BC,若 AE:EB=m,BD:DC=n,则( )
A. 若 m>1,n>1,则 2S△AEF>S△ABD B. 若 m>1,n<1,则 2S△AEF<S△ABD
C. 若 m<1,n<1,则 2S△AEF<S△ABD D. 若 m<1,n>1,则 2S△AEF<S△ABD
9、如图,在正方形ABCD中,AB=4 .E,F分别为边AB,BC的中点,连接AF,DE,点N,M分别为AF,DE的中点,连接MN,则MN的长为( )
A. B. 2 C. D. 2
10、如图,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接并延长AE交CD于F,连接BD分别交CE、AF于G、H,下列结论:①∠CEH=45°;②GF∥DE;③2OH+DH=BD;④BG=DG;⑤S△BEC:S△BGC= 。其中正确的结论是( )
A. ①②③ B. ①②④ C. ①②⑤ D. ②④⑤
二、填空题
1、已知线段a=3,b=27,则a,b的比例中项线段长等于________.
2、如图是用卡钳测量容器内径的示意图,现量得卡钳上 , 两个端点之间的距离为 , ,则容器的内径是________.
3、在平面直角坐标中,△ABC的顶点坐标分别是A(1,1),B(4,2),C(3,5),以点A为位似中心,相似比为1:把三角形ABC缩小,得到△AB1C1 , 则点C的对应点C1的坐标为 .
4、如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则 的值为 .
5、如图,已知正方形ABCD的边长为1,点M是BC边上的动点(不与B,C重合),点N是AM的中点,过点N作EF⊥AM,分别交AB,BD,CD于点E,K,F,设BM=x.
( 1 )AE的长为________(用含x的代数式表示);
( 2 )设EK=2KF,则 的值为________.
6、如图,在矩形ABCD中,AD= AB , ∠BAD的平分线交BC于点E , DH⊥AE于点H , 连接BH并延长交CD于点F , 连接DE交BF于点O , 下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF , 其中正确的有________.
三、解答题
1、如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积.
2、如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3 , AF=2 , 求AE的长.
3、如图,为了测量一栋楼的高度 ,小明同学先在操场上 处放一面镜子,向后退到 处,恰好在镜子中看到楼的顶部 ;再将镜子放到 处,然后后退到 处,恰好再次在镜子中看到楼的顶部 ( 在同一条直线上).测得 , ,如果小明眼睛距地面高度 为 ,试确定楼的高度 .
4、如图,在 ABCD中,对角线AC⊥BC,∠BAC=30°,BC=2 ,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,求 AF长。
5、感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6 ,CE=4,求DE的长
6、如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.
7、已知:Rt△A′BC′≌Rt△ABC,∠A′C′B=∠ACB=90°,∠A′BC′=∠ABC=60°,Rt△A′BC′可绕点B旋转,设旋转过程中直线CC′和AA′相交于点D.
(1)如图1所示,当点C′在AB边上时,判断线段AD和线段A′D之间的数量关系,并证明你的结论;
(2)将Rt△A′BC′由图1的位置旋转到图2的位置时,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)将Rt△A′BC′由图1的位置按顺时针方向旋转α角(0°≤α≤120°),当A、C′、A′三点在一条直线上时,请直接写出旋转角的度数.
8、如图 ,在 中, , ,点D是AC的中点,连接BD,过点C作CE平分 交BD于点E,点F在AB上,且
(1)求证: ;
(2)如图②,过点A作 交BD的延长线于点G,
①若 ,求CF; ②设CF交BD于H,求 的值.
9、如图
(1)如图1,在△ABC中,AB>AC,点D,E分别在边AB,AC上,且DE∥BC,若AD=2,AE= ,则 的值是________;
(2)如图2,在(1)的条件下,将△ADE绕点A逆时针方向旋转一定的角度,连接CE和BD, 的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
(3)如图3,在四边形ABCD中,AC⊥BC于点C,∠BAC=∠ADC=θ,且tanθ= ,当CD=6,AD=3时,请直接写出线段BD的长度.
答案解析部分
一、单选题
1. C 2. C 3.C 4.A 5.A 6.D 7.C 8.D 9.C 10.C
二、填空题
1.9 2. 15cm 3. (2,3)或(0,-1) 4. 5. ;x 6. ①②③④
三、解答题
1.【答案】 解答:由已知得,DG∥BC∴△ADG∽△ABC,∵AH⊥BC∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m)= ,即DG= =50(m),∴S矩形DEFG=DE×DG=2000(m2).
2.【答案】 证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠B+∠C=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC;
(2)解:∵四边形ABCD是平行四边形,
∴CD=AB=4,
由(1)知△ADF∽△DEC,
∴ ,
∴DE= .
在Rt△ADE中,由勾股定理得:AE= .
3.【答案】 解:设 关于点 的对称点为 ,由光的反射定律知,延长 相交于 ,
连接 并延长交 于 ,
∥ , ∽ ,
,
即 ,
,
.
答:楼的高度 为32米。
4.【答案】 解:如图,连接PC交AB于T,作PN⊥AB于N,CM⊥PC交PE的延长线于M.
∵AC⊥BC,
∴∠ACB=90°,
∵BC= ,∠BAC=30°,
∴AB=2BC= ,AC= BC=6,∠ABC=60°,
∵∠EPB=∠EBP=60°,
∴△EPB是等边三角形,
∴∠PEB=60°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BCE=180°﹣∠ABC=120°,
∴∠EPB+∠BCE=180°,
∴P,B,C,E四点共圆,
∴∠PCB=∠PEB=60°,∠MPC=∠EBC,
∵∠TCB=∠CBT=60°
∴△TCB是等边三角形,
∴∠BCT=60°,∠ACT=30°,BT=BC=AT= ,
∵∠BAG=∠BAC=30°,
∴∠APC=90°,
∴PA=AT cos30°=3,AN=PA cos30°= ,PN= PA= ,PC= PA= ,
∴BN=AB﹣AN= ,
∵∠PBE=∠CBT=60°,
∴∠PBN=∠CBE=∠CPM,
∵∠PCM=∠PNB=90°,
∴△PCM∽△BNP,
∴ ,
∴ ,
∴CM= ,
∵PA⊥PC,CM⊥PC,
∴CM∥PA,
∴ ,
∴AF= AC= .
故答案为 .
5.【答案】 解:感知:∵∠APD=90°,
∴∠APB+∠DPC=90°,
∵∠B=90°,
∴∠APB+∠BAP=90°,
∴∠BAP=∠DPC,
∵AB∥CD,∠B=90°,
∴∠C=∠B=90°,
∴△ABP∽△DCP.
探究:∵∠APC=∠BAP+∠B,∠APC=∠APD+∠CPD,
∴∠BAP+∠B=∠APD+∠CPD.
∵∠B=∠APD,
∴∠BAP=∠CPD.
∵∠B=∠C,
∴△ABP∽△PCD,
拓展:同探究的方法得出,△BDP∽△CPE,
∴ ,
∵点P是边BC的中点,
∴BP=CP=3 ,
∵CE=4,
∴ ,
∴BD= ,
∵∠B=∠C=45°,
∴∠A=180°﹣∠B﹣∠C=90°,
即AC⊥AB且AC=AB=6,
∴AD=AB﹣BD=6﹣ = ,AE=AC﹣CE=6﹣4=2,
在Rt△ADE中,DE= .
6.【答案】 (1)解:PM=PN,PM⊥PN,理由如下:
∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中
,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠EAC=∠CBD,
∵点M、N分别是斜边AB、DE的中点,点P为AD的中点,
∴PM= BD,PN= AE,
∴PM=PN,
∵PM∥BD,PN∥AE,AE⊥BD,
∴∠NPD=∠EAC,∠MPA=∠BDC,∠EAC+∠BDC=90°,
∴∠MPA+∠NPC=90°,
∴∠MPN=90°,
即PM⊥PN.
(2)解:∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,
∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD.
∴△ACE≌△BCD.
∴AE=BD,∠CAE=∠CBD.
又∵∠AOC=∠BOE,
∠CAE=∠CBD,
∴∠BHO=∠ACO=90°.
∵点P、M、N分别为AD、AB、DE的中点,
∴PM= BD,PM∥BD;
PN= AE,PN∥AE.
∴PM=PN.
∴∠MGE+∠BHA=180°.
∴∠MGE=90°.
∴∠MPN=90°.
∴PM⊥PN
(3)解:PM=kPN
∵△ACB和△ECD是直角三角形,
∴∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD.
∵BC=kAC,CD=kCE,
∴ =k.
∴△BCD∽△ACE.
∴BD=kAE.
∵点P、M、N分别为AD、AB、DE的中点,
∴PM= BD,PN= AE.
∴PM=kPN.
7.【答案】 答:(1)AD=A′D.证明:如图1,∵Rt△A′BC′≌Rt△ABC,∴BC=BC′,BA=BA′.∵∠A′BC′=∠ABC=60°,∴△BCC′和△BAA′都是等边三角形.∴∠BAA′=∠BC′C=60°.∵∠A′C′B=90°,∴∠DC′A′=30°.∵∠AC′D=∠BC′C=60°,∴∠ADC′=60°.∴∠DA′C′=30°.∴∠DAC′=∠DC′A,∠DC′A′=∠DA′C′.∴AD=DC′,DC′=DA′.∴AD=A′D.(2)仍然成立:AD=A′D.证法一:利用相似.如图2﹣1.由旋转可得,BA=BA′,BC=BC′,∠CBC′=∠ABA′∵∠1=(180°﹣∠ABA′),∠3=(180°﹣∠CBC′)∴∠1=∠3.设AB、CD交于点O,则∠AOD=∠BOC∴△BOC∽△DOA.∴∠2=∠4,= . 连接BD,∵∠BOD=∠COA,∴△BOD∽△COA.∴∠5=∠6.∵∠ACB=90°,∴∠2+∠5=90°.∴∠4+∠6=90°,即∠ADB=90°.∵BA=BA′,∠ADB=90°,∴AD=A′D.证法二:利用全等.如图2﹣2.过点A作AE∥A′C′,交CD的延长线于点E,则∠1=∠2,∠E=∠3.由旋转可得,AC=A′C′,BC=BC′,∴∠4=∠5.∵∠ACB=∠A′C′B=90°,∴∠5+∠6=∠3+∠4=90°,∴∠3=∠6.∴∠E=∠6,∴AE=AC=A′C′.在△ADE与△A′DC′中,∴△ADE≌△A′DC′(ASA),∴AD=A′D.(3)当A、C′、A′三点在一条直线上时,如图3,则有∠AC′B=180°﹣∠A′C′B=90°.在Rt△ACB和Rt△AC′B中, . ∴Rt△ACB≌Rt△AC′B (HL).∴∠ABC=∠ABC′=60°.∴当A、C′、A′三点在一条直线上时,旋转角α的度数为60°.
8.【答案】 (1)解:如图①, , ,
,
平分 ,
,
,
在 和 中,
≌ ,
;
(2)解:①如图②,延长CE,交AB于点M,
,CM平分 ,
是AB的中点, ,
,
,即 ,
, ,
, ,
≌ ,
,
,
②由①可知, , ,
设 ,则 ,所以 ,所以 ,
由勾股定理得: ,
,
,
, ,
,
∽ ,
.
9.【答案】 (1)
(2)解: 的值不变化,值为 ;理由如下:
由(1)得:DE∥BC,
∴△ADE∽△ABC,
∴ = ,
由旋转的性质得:∠BAD=∠CAE,
∴△ABD∽△ACE,
∴ = =
(3)解:作AE⊥CD于E,DM⊥AC于M,DN⊥BC于N,如图3所示:
则四边形DMCN是矩形,
∴DM=CN,DN=MC,
∵∠BAC=∠ADC=θ,且tanθ= ,
∴ = , = ,
∴ = ,
∴AE= AD= ×3= ,DE= AE= ,
∴CE=CD﹣DE=6﹣ = ,
∴AC= = =
∴BC= AC= ,
∵△ACD的面积= AC×DM= CD×AE,
∴CN=DM= = ,
∴BN=BC+CN= ,AM= = = ,
∴DN=MC=AM+AC=
∴BD= = =
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
