24.3正多边形和圆 同步作业-2021-2022学年九年级上册数学人教版(Word版含答案)
文档属性
| 名称 | 24.3正多边形和圆 同步作业-2021-2022学年九年级上册数学人教版(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 183.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 00:00:00 | ||
图片预览


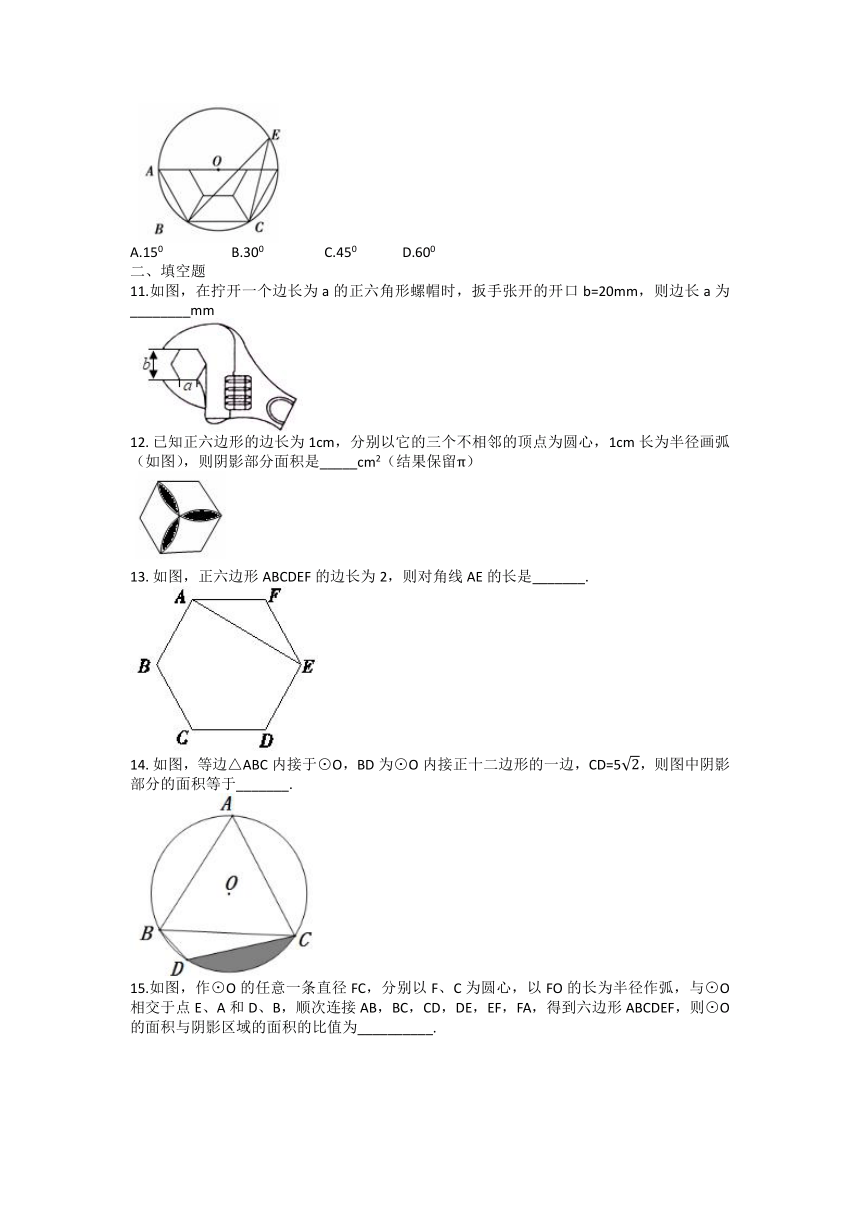
文档简介
24.2.3正多边形与圆作业
一、选择题
1.如图,若干全等正五边形排成环状,图中所示的是前3个五边形,要完成一圆环还需( )个五边形。
A.6 B.7 C.8 D.9
2.割圆术是我国古代数学家刘微创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”。试用这个方法解决问题:如图,⊙的内接多边形周长为3,圆的外切多边形周长为3.4,则下列各数中与此圆的周长最接近的是( )。
B. C. D.
3.有一圆内接正八边形ABCDEFGH,若△ADE的面积为10,则正八边形ABCDEFGH的面积为( )
A.40 B.50 C.60 D.80
4.如图,有两个半径差为1的圆,它们各有一个内接正八边形,已知阴影部分的面积是4,则可知大圆半径是( )
B.3 C.2 D.
5.如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于( )
A.300 B.450 C.550 D.600
6.如图,四边形OBCA为正方形,图1是以AB为直径画半圆,阴影部分面积记为S1,图2是以O为圆心,OA长为半径画弧,阴影部分面积记为S2,则S1,S2的大小关系为( )
S1S2 D.无法判断
7.一张圆心角为450的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
A.5:4 B.5:2 C. D.
8.如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为( )
A.4 B.6 C.8 D.12
9.如图,点O为正六边形ABCDEF对角线FD上一点,S△AFO=8,S△CDO=2,则S正六边形ABCDEF的值是()
A.20 B.30 C.40 D.随点O位置而变化
10 如图,圆内接四边形ABCD是由四个全等的等腰梯形组成,AD是⊙O的直径,则∠BEC的度数为( )
A.150 B.300 C.450 D.600
填空题
11.如图,在拧开一个边长为a的正六角形螺帽时,扳手张开的开口b=20mm,则边长a为________mm
已知正六边形的边长为1cm,分别以它的三个不相邻的顶点为圆心,1cm长为半径画弧(如图),则阴影部分面积是_____cm2(结果保留)
如图,正六边形ABCDEF的边长为2,则对角线AE的长是_______.
如图,等边△ABC内接于⊙O,BD为⊙O内接正十二边形的一边,CD=5,则图中阴影部分的面积等于_______.
15.如图,作⊙O的任意一条直径FC,分别以F、C为圆心,以FO的长为半径作弧,与⊙O相交于点E、A和D、B,顺次连接AB,BC,CD,DE,EF,FA,得到六边形ABCDEF,则⊙O的面积与阴影区域的面积的比值为__________.
16.如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的阴影部分的面积为_______。
三、解答题
17.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆
正方形ABCD与正六边形AEFCGH的边长之比为______
连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由。
18.如图1,2,3,...,m,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,...正n边形ABCDEF...的边AB,BC上的点,且BM=CN,连接OM,ON.
f求图1中∠MON的度数;
图2中∠MON的度数是_____9000,图3∠MON的度数是_____720
试探究∠MON的度数与正n边形边数n的关系(直接答案)
19.如图,正方形ABCD内接于⊙O,P为弧BC上的一点,连接DP,CP。
求∠CPD的度数
当点P为弧BC的中点时,CP是⊙O的内接正n边形的一边,求n
20.如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N。
求证:AF=FB;
在不添加任何辅助线的情况下,请直接写出所有与△ABM全等的三角形。
参考答案
选择题
A 2.C 3.A 4.A 5.B 6.B 7.A 8.D 9.B 10.B
填空题
2
80
解答题
(1)
(2)解:BE是⊙O的内接正十二边形的一边
理由:连接OA,OB,OE
在正方形ABCD中,
∠AOB=900
在正六边形AEFCGH中,∠AOE=600
∴∠BOE=300
∵n==12
∴BE是正十二边形的边
18.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是_____900,图3∠MON的度数是_____720
(3)试探究∠MON的度数与正n边形边数n的关系(直接答案)
解:(1)∵BM=CN,AB=BC
∴AM=BN
∵OA=OB,∠OAM=∠OBN=300
∴△AOM≌△BON
∴∠MOA=∠NOB
∴∠MON=∠AOM+∠MOB=∠AOB
∵三角形ABC是圆内接正三角形
∴∠ACB=600
∴∠MON=∠AOB=1200
19.解:(1)连接OD,OC
则∠DOC=900
∴∠CPD==450
(2)连接OP,OB
∵点P为弧BC的中点
∴弧CP=弧BP
∴∠COP=∠POB=450
∵n==8
∴BE是正八边形的边
20.
一、选择题
1.如图,若干全等正五边形排成环状,图中所示的是前3个五边形,要完成一圆环还需( )个五边形。
A.6 B.7 C.8 D.9
2.割圆术是我国古代数学家刘微创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”。试用这个方法解决问题:如图,⊙的内接多边形周长为3,圆的外切多边形周长为3.4,则下列各数中与此圆的周长最接近的是( )。
B. C. D.
3.有一圆内接正八边形ABCDEFGH,若△ADE的面积为10,则正八边形ABCDEFGH的面积为( )
A.40 B.50 C.60 D.80
4.如图,有两个半径差为1的圆,它们各有一个内接正八边形,已知阴影部分的面积是4,则可知大圆半径是( )
B.3 C.2 D.
5.如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于( )
A.300 B.450 C.550 D.600
6.如图,四边形OBCA为正方形,图1是以AB为直径画半圆,阴影部分面积记为S1,图2是以O为圆心,OA长为半径画弧,阴影部分面积记为S2,则S1,S2的大小关系为( )
S1
7.一张圆心角为450的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
A.5:4 B.5:2 C. D.
8.如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为( )
A.4 B.6 C.8 D.12
9.如图,点O为正六边形ABCDEF对角线FD上一点,S△AFO=8,S△CDO=2,则S正六边形ABCDEF的值是()
A.20 B.30 C.40 D.随点O位置而变化
10 如图,圆内接四边形ABCD是由四个全等的等腰梯形组成,AD是⊙O的直径,则∠BEC的度数为( )
A.150 B.300 C.450 D.600
填空题
11.如图,在拧开一个边长为a的正六角形螺帽时,扳手张开的开口b=20mm,则边长a为________mm
已知正六边形的边长为1cm,分别以它的三个不相邻的顶点为圆心,1cm长为半径画弧(如图),则阴影部分面积是_____cm2(结果保留)
如图,正六边形ABCDEF的边长为2,则对角线AE的长是_______.
如图,等边△ABC内接于⊙O,BD为⊙O内接正十二边形的一边,CD=5,则图中阴影部分的面积等于_______.
15.如图,作⊙O的任意一条直径FC,分别以F、C为圆心,以FO的长为半径作弧,与⊙O相交于点E、A和D、B,顺次连接AB,BC,CD,DE,EF,FA,得到六边形ABCDEF,则⊙O的面积与阴影区域的面积的比值为__________.
16.如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的阴影部分的面积为_______。
三、解答题
17.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆
正方形ABCD与正六边形AEFCGH的边长之比为______
连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由。
18.如图1,2,3,...,m,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,...正n边形ABCDEF...的边AB,BC上的点,且BM=CN,连接OM,ON.
f求图1中∠MON的度数;
图2中∠MON的度数是_____9000,图3∠MON的度数是_____720
试探究∠MON的度数与正n边形边数n的关系(直接答案)
19.如图,正方形ABCD内接于⊙O,P为弧BC上的一点,连接DP,CP。
求∠CPD的度数
当点P为弧BC的中点时,CP是⊙O的内接正n边形的一边,求n
20.如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N。
求证:AF=FB;
在不添加任何辅助线的情况下,请直接写出所有与△ABM全等的三角形。
参考答案
选择题
A 2.C 3.A 4.A 5.B 6.B 7.A 8.D 9.B 10.B
填空题
2
80
解答题
(1)
(2)解:BE是⊙O的内接正十二边形的一边
理由:连接OA,OB,OE
在正方形ABCD中,
∠AOB=900
在正六边形AEFCGH中,∠AOE=600
∴∠BOE=300
∵n==12
∴BE是正十二边形的边
18.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是_____900,图3∠MON的度数是_____720
(3)试探究∠MON的度数与正n边形边数n的关系(直接答案)
解:(1)∵BM=CN,AB=BC
∴AM=BN
∵OA=OB,∠OAM=∠OBN=300
∴△AOM≌△BON
∴∠MOA=∠NOB
∴∠MON=∠AOM+∠MOB=∠AOB
∵三角形ABC是圆内接正三角形
∴∠ACB=600
∴∠MON=∠AOB=1200
19.解:(1)连接OD,OC
则∠DOC=900
∴∠CPD==450
(2)连接OP,OB
∵点P为弧BC的中点
∴弧CP=弧BP
∴∠COP=∠POB=450
∵n==8
∴BE是正八边形的边
20.
同课章节目录
