24.4弧长与扇形面积 同步作业-2021-2022学年九年级上册数学人教版(Word版含答案)
文档属性
| 名称 | 24.4弧长与扇形面积 同步作业-2021-2022学年九年级上册数学人教版(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 173.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 09:07:28 | ||
图片预览

文档简介
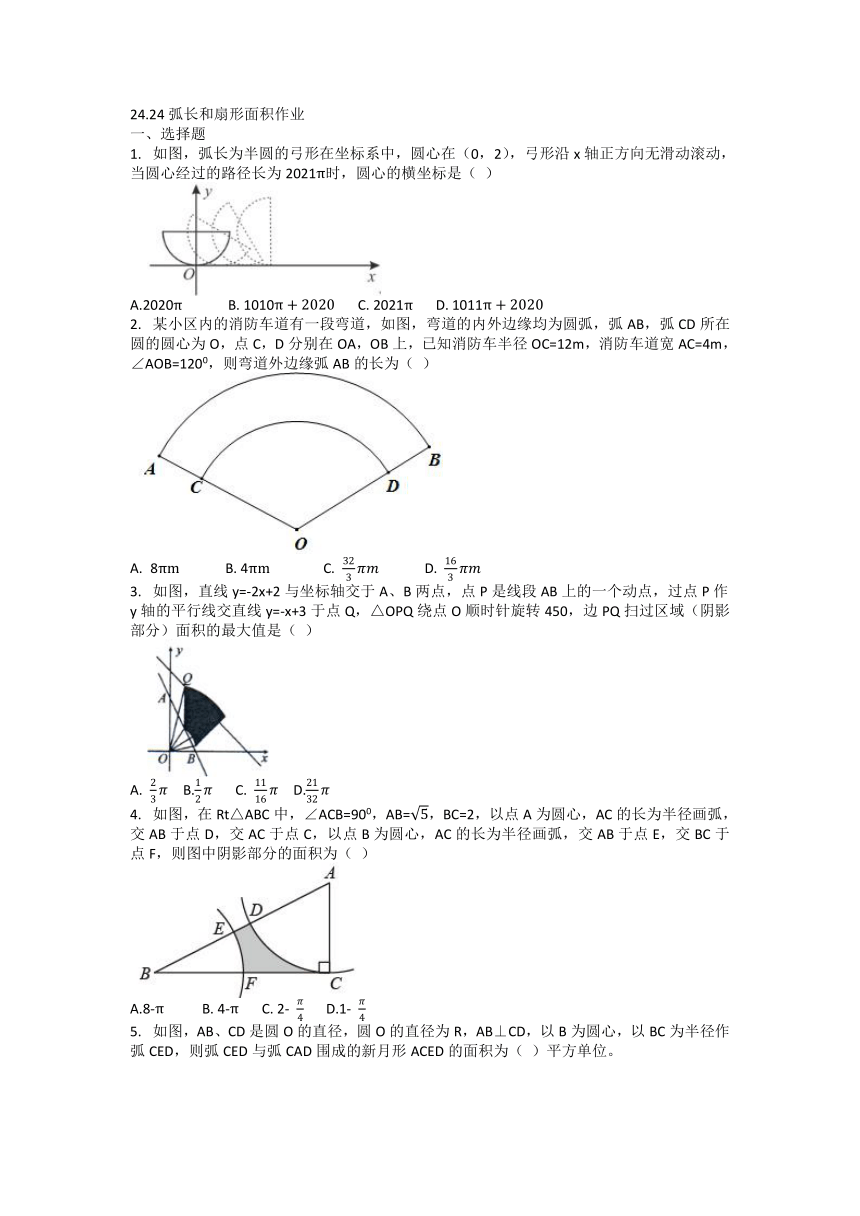
24.24弧长和扇形面积作业
选择题
如图,弧长为半圆的弓形在坐标系中,圆心在(0,2),弓形沿x轴正方向无滑动滚动,当圆心经过的路径长为2021时,圆心的横坐标是( )
A.2020 B. 1010 C. 2021 D. 1011
某小区内的消防车道有一段弯道,如图,弯道的内外边缘均为圆弧,弧AB,弧CD所在圆的圆心为O,点C,D分别在OA,OB上,已知消防车半径OC=12m,消防车道宽AC=4m,∠AOB=1200,则弯道外边缘弧AB的长为( )
8 B. 4 C. D.
如图,直线y=-2x+2与坐标轴交于A、B两点,点P是线段AB上的一个动点,过点P作y轴的平行线交直线y=-x+3于点Q,△OPQ绕点O顺时针旋转450,边PQ扫过区域(阴影部分)面积的最大值是( )
B. C. D.
如图,在Rt△ABC中,∠ACB=900,AB=,BC=2,以点A为圆心,AC的长为半径画弧,交AB于点D,交AC于点C,以点B为圆心,AC的长为半径画弧,交AB于点E,交BC于点F,则图中阴影部分的面积为( )
A.8- B. 4- C. 2- D.1-
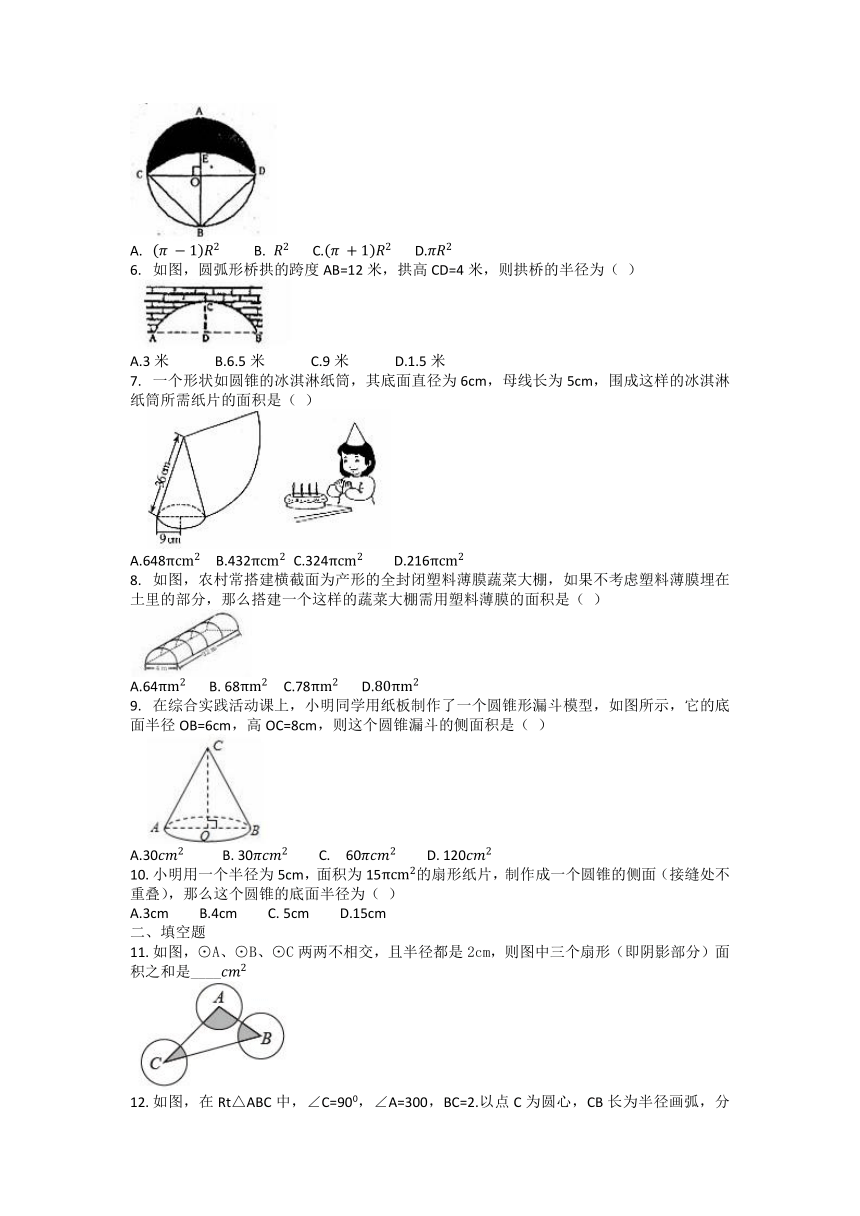
如图,AB、CD是圆O的直径,圆O的直径为R,AB⊥CD,以B为圆心,以BC为半径作弧CED,则弧CED与弧CAD围成的新月形ACED的面积为( )平方单位。
B. C. D.
如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为( )
A.3米 B.6.5米 C.9米 D.1.5米
一个形状如圆锥的冰淇淋纸筒,其底面直径为6cm,母线长为5cm,围成这样的冰淇淋纸筒所需纸片的面积是( )
A.648 B.432 C.324 D.216
如图,农村常搭建横截面为产形的全封闭塑料薄膜蔬菜大棚,如果不考虑塑料薄膜埋在土里的部分,那么搭建一个这样的蔬菜大棚需用塑料薄膜的面积是( )
A.64 B. 68 C.78 D.
在综合实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径OB=6cm,高OC=8cm,则这个圆锥漏斗的侧面积是( )
A.30 B. 30 C. 60 D. 120
小明用一个半径为5cm,面积为15的扇形纸片,制作成一个圆锥的侧面(接缝处不重叠),那么这个圆锥的底面半径为( )
A.3cm B.4cm C. 5cm D.15cm
填空题
如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积之和是____
如图,在Rt△ABC中,∠C=900,∠A=300,BC=2.以点C为圆心,CB长为半径画弧,分别交AC,AB于点D,E,则图中阴影部分的面积为_______(结果保留)
已知圆锥的母线长为10,高为8,则该圆锥的侧面展开图的弧长为________.(用含),圆心角为________度。
如图,将△ABC绕点C顺时针旋转1200得到△A`B`C`。已知AC=3,BC=2,则线段AB扫过的图形(阴影部分)的面积为________.
若一个圆锥的底面半径为1cm,它的侧面展开图的圆心角为900,则这个圆锥的母线长为______cm
如图所示,用一个半径为60cm,圆心角为1500的扇形围成一个圆锥,则这个圆锥的底面半径为______cm
解答题
如图,一条公路的转变处是一段圆弧CD,点O是弧CD所在圆的圆心,其中CD=600m,E为弧CD上一点,且OE⊥CD,垂足为F,EF=90m,求这段弯路的半径。
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转900得到△AB1C1.
在正方形网格中,作出△AB1C1;(不要求写作法)
设网格小正方形的边长为1cm,用阴影表示出旋转过程中线段BC所扫过的图形,然后求出它的面积。(结果保留)
如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD。
求证:AD平分∠BAC;
若∠BAC=600,OA=2,求阴影部分的面积(结果保留)
参考答案
选择题
D 2.C 3.A 4.D 5.B 6.B 7.C 8.C 9.B 10.A
填空题
2
12
4
25
解答题
17.解:∵O为圆心,OE⊥CD于F
∴CF==300cm
设所在圆半径为r,则
r=545m
答:这段弯路的半径545m
18.解:(1)作图如下:
线段BC所扫过的图形如图所示
根据网格图知:AB=4,BC=3,
所以由勾股定理得 AC=5
线段BC所扫过的图形的面积S==
19.解:(1)证明:∵⊙O切BC于D
∴OD⊥BC
∵AC⊥BC
∴AC∥OD
∴∠CAD=∠ADO
∵OA=OD
∴∠OAD=∠ADO
∴∠OAD=∠CAD
即AD平分∠CAB
设EO与AD交于点M,连接ED
∵∠BAC=600,OA=OE
∴△AEO是等边三角形
∴AE=OA, ∠AOE=600
∴AE=AO=OD
又由(1)知,AC∥OD即AE∥OD
∴四边 形AEDO是菱形,则△AEM≌△DMO,∠EOD=600
∴S△AEM=S△DMO
∴S阴影=S扇形EOD=
选择题
如图,弧长为半圆的弓形在坐标系中,圆心在(0,2),弓形沿x轴正方向无滑动滚动,当圆心经过的路径长为2021时,圆心的横坐标是( )
A.2020 B. 1010 C. 2021 D. 1011
某小区内的消防车道有一段弯道,如图,弯道的内外边缘均为圆弧,弧AB,弧CD所在圆的圆心为O,点C,D分别在OA,OB上,已知消防车半径OC=12m,消防车道宽AC=4m,∠AOB=1200,则弯道外边缘弧AB的长为( )
8 B. 4 C. D.
如图,直线y=-2x+2与坐标轴交于A、B两点,点P是线段AB上的一个动点,过点P作y轴的平行线交直线y=-x+3于点Q,△OPQ绕点O顺时针旋转450,边PQ扫过区域(阴影部分)面积的最大值是( )
B. C. D.
如图,在Rt△ABC中,∠ACB=900,AB=,BC=2,以点A为圆心,AC的长为半径画弧,交AB于点D,交AC于点C,以点B为圆心,AC的长为半径画弧,交AB于点E,交BC于点F,则图中阴影部分的面积为( )
A.8- B. 4- C. 2- D.1-
如图,AB、CD是圆O的直径,圆O的直径为R,AB⊥CD,以B为圆心,以BC为半径作弧CED,则弧CED与弧CAD围成的新月形ACED的面积为( )平方单位。
B. C. D.
如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为( )
A.3米 B.6.5米 C.9米 D.1.5米
一个形状如圆锥的冰淇淋纸筒,其底面直径为6cm,母线长为5cm,围成这样的冰淇淋纸筒所需纸片的面积是( )
A.648 B.432 C.324 D.216
如图,农村常搭建横截面为产形的全封闭塑料薄膜蔬菜大棚,如果不考虑塑料薄膜埋在土里的部分,那么搭建一个这样的蔬菜大棚需用塑料薄膜的面积是( )
A.64 B. 68 C.78 D.
在综合实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径OB=6cm,高OC=8cm,则这个圆锥漏斗的侧面积是( )
A.30 B. 30 C. 60 D. 120
小明用一个半径为5cm,面积为15的扇形纸片,制作成一个圆锥的侧面(接缝处不重叠),那么这个圆锥的底面半径为( )
A.3cm B.4cm C. 5cm D.15cm
填空题
如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积之和是____
如图,在Rt△ABC中,∠C=900,∠A=300,BC=2.以点C为圆心,CB长为半径画弧,分别交AC,AB于点D,E,则图中阴影部分的面积为_______(结果保留)
已知圆锥的母线长为10,高为8,则该圆锥的侧面展开图的弧长为________.(用含),圆心角为________度。
如图,将△ABC绕点C顺时针旋转1200得到△A`B`C`。已知AC=3,BC=2,则线段AB扫过的图形(阴影部分)的面积为________.
若一个圆锥的底面半径为1cm,它的侧面展开图的圆心角为900,则这个圆锥的母线长为______cm
如图所示,用一个半径为60cm,圆心角为1500的扇形围成一个圆锥,则这个圆锥的底面半径为______cm
解答题
如图,一条公路的转变处是一段圆弧CD,点O是弧CD所在圆的圆心,其中CD=600m,E为弧CD上一点,且OE⊥CD,垂足为F,EF=90m,求这段弯路的半径。
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转900得到△AB1C1.
在正方形网格中,作出△AB1C1;(不要求写作法)
设网格小正方形的边长为1cm,用阴影表示出旋转过程中线段BC所扫过的图形,然后求出它的面积。(结果保留)
如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD。
求证:AD平分∠BAC;
若∠BAC=600,OA=2,求阴影部分的面积(结果保留)
参考答案
选择题
D 2.C 3.A 4.D 5.B 6.B 7.C 8.C 9.B 10.A
填空题
2
12
4
25
解答题
17.解:∵O为圆心,OE⊥CD于F
∴CF==300cm
设所在圆半径为r,则
r=545m
答:这段弯路的半径545m
18.解:(1)作图如下:
线段BC所扫过的图形如图所示
根据网格图知:AB=4,BC=3,
所以由勾股定理得 AC=5
线段BC所扫过的图形的面积S==
19.解:(1)证明:∵⊙O切BC于D
∴OD⊥BC
∵AC⊥BC
∴AC∥OD
∴∠CAD=∠ADO
∵OA=OD
∴∠OAD=∠ADO
∴∠OAD=∠CAD
即AD平分∠CAB
设EO与AD交于点M,连接ED
∵∠BAC=600,OA=OE
∴△AEO是等边三角形
∴AE=OA, ∠AOE=600
∴AE=AO=OD
又由(1)知,AC∥OD即AE∥OD
∴四边 形AEDO是菱形,则△AEM≌△DMO,∠EOD=600
∴S△AEM=S△DMO
∴S阴影=S扇形EOD=
同课章节目录
