2.2.1 函数y-ax2的图象与性质 课件(共24张PPT)
文档属性
| 名称 | 2.2.1 函数y-ax2的图象与性质 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:56:23 | ||
图片预览




文档简介
(共24张PPT)
§2.2 y=ax2的图象与性质
北师版九年级下册 二次函数
学习目标
1.经历探索二次函数图象的画法和性质的过程,获得利用图象研究函数性质的经验.(重点)
2.能够利用描点法作出y=x2的图象,并能根据图象认识和理解二次函数y=x2的性质.;(重点)
3.根据作出的二次函数y=-x2与y=x2的图象的异同比较,初步建立二次函数表达式与图象间的联系.理解表达式中,系数对图象的影响.(难点)
1.二次函数的定义
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.
(1)列表.
(3)连线.
(2)描点.
2.画函数图象的主要步骤是什么?
温 故 知 新
二次函数y=x2的图象与性质
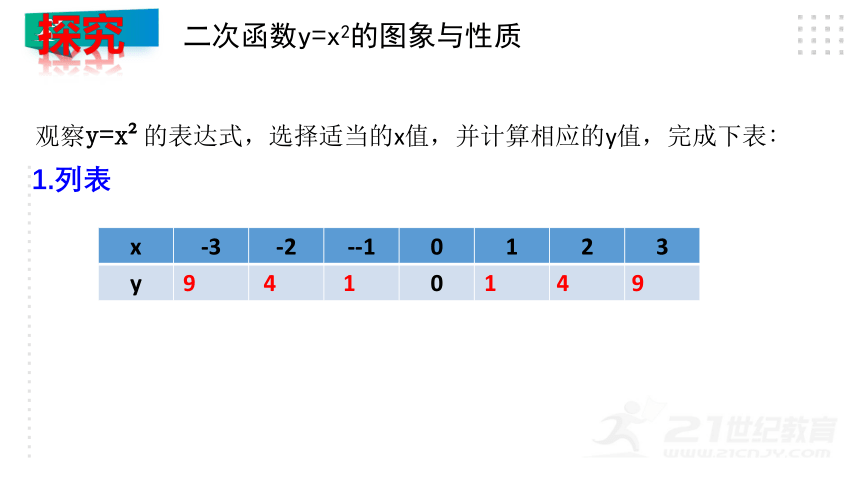
观察y=x 的表达式,选择适当的x值,并计算相应的y值,完成下表∶
x -3 -2 --1 0 1 2 3
y 0
探究
1
1
4
4
9
9
1.列表
x
y
O
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
y=x2
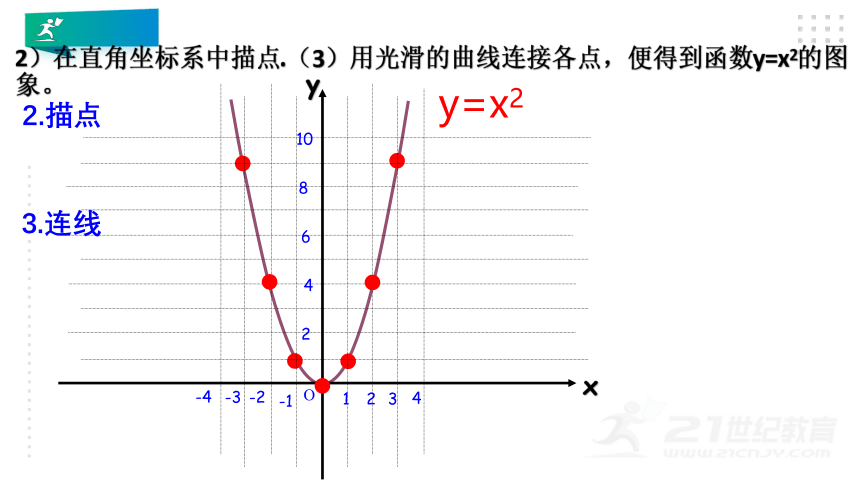
2.描点
3.连线
2)在直角坐标系中描点.(3)用光滑的曲线连接各点,便得到函数y=x2的图象。
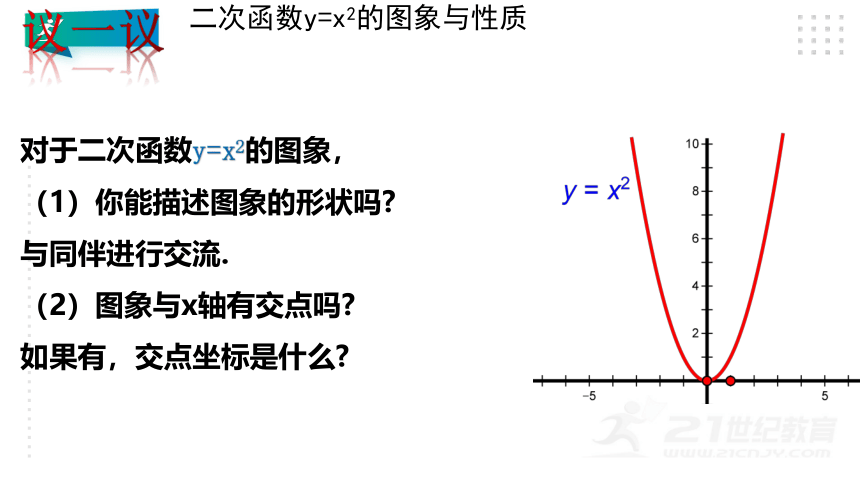
对于二次函数y=x2的图象,
(1)你能描述图象的形状吗
与同伴进行交流.
(2)图象与x轴有交点吗
如果有,交点坐标是什么
议一议
二次函数y=x2的图象与性质
二次函数y=x2的图象与性质
交流:
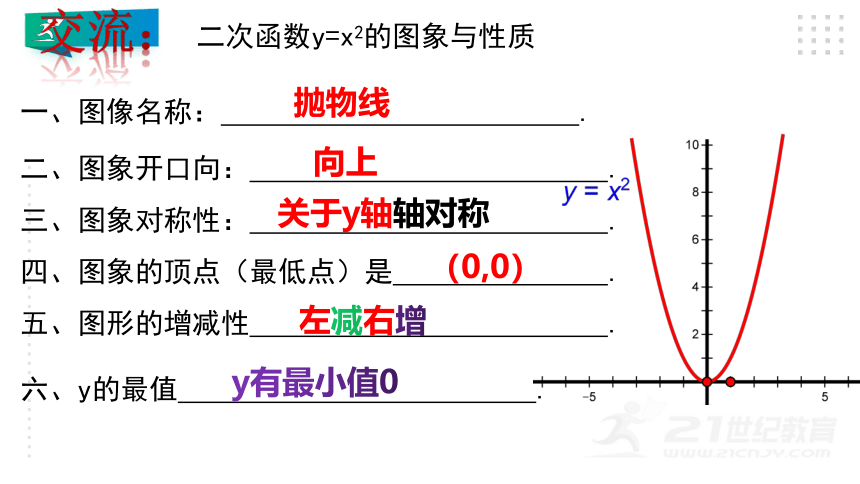
一、图像名称: .
二、图象开口向: .
三、图象对称性: .
四、图象的顶点(最低点)是 .
五、图形的增减性 .
六、y的最值 .
抛物线
向上
关于y轴轴对称
(0,0)
左减右增
y有最小值0
二次函数y=x 的图象是一条抛物线(parabola).它的
开口向上,且关于y轴对称。对称轴与抛物线的交点是抛物线的顶点、它是图象的最低点.
二次函数y=x2的图象与性质
总结:
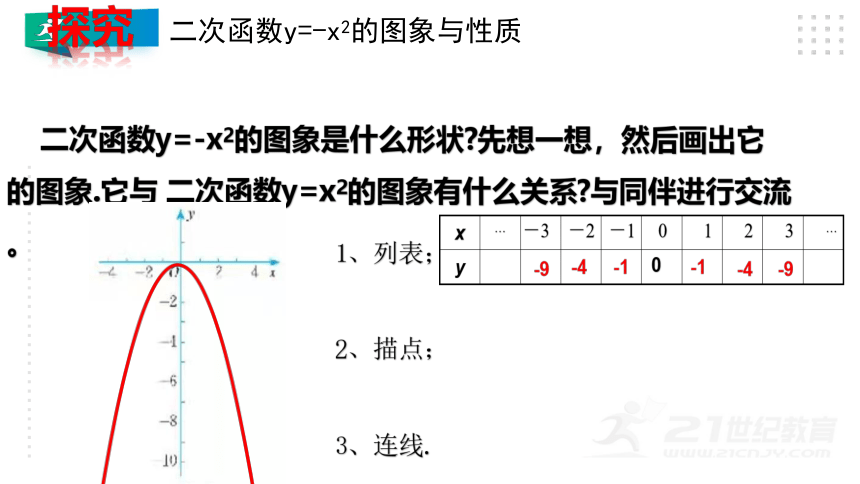
二次函数y=-x2的图象是什么形状 先想一想,然后画出它的图象.它与 二次函数y=x2的图象有什么关系 与同伴进行交流。
二次函数y=-x2的图象与性质
探究
1、列表;
2、描点;
3、连线.
关于y=x2与y=-x2的相同与不同点。
二者相同点:(1)均为抛物线;(2)图象过原点;(3)均关于y轴对称.
二者不同点:(1)开口方向; (2)增减性;(3)y有最大(小)值
交流:
交流:
关于y=ax2的图象与性质。
a=1
(a>0)
开口
向上
关于
y轴对称
左减右增
a=-1
(a<0)
开口
向下
关于
y轴对称
左增右减
※二次项系数a对图像的影响:(1)开口方向;(2)增减性.
y=x2
y=-x2
观察y=2x2,y=-
议一议
的图象,并说一说你有什么发现?
通过对比观察,可以初步推断
二次函数y=ax2(a为不等于0的任意实数):
当a>0时,图象、性质与a=1时大致相同;
当a<0时,图象、性质与a=-1时大致相同.
唯一不同的地方,就是开口的大小。
二次项系数a对图象的影响:
1、图象的开口方向
探究:
a>0,图象开口向上.
a<0,图象开口向下.
2、y与x的增减性
a>0,左减右增.
a<0,左增右减.
3、开口大小
当a>0时,
a的绝对值越大,开口越小.
发现:
当a<0时,
a的绝对值越大,开口越小.
综合归纳
二次项系数a对图象的影响:
a>0
a<0
开口向上
开口向下
左减右增
左增右减
y有最小值0
y有最大值0
值越大,
口越小
把图中图象的号码,填在它的函数式后面:(填序号)
(1)y=3x2的图象是_______;
(2)y= x2的图象是_______;
(3)y=-x2的图象是_______;
(4)y= x2的图象是_______.
变式训练
③
①
④
②
3.函数y= x2的图象的开口 ,对称轴是 ,顶点是 ;顶点是抛物线的最____点.
2.函数y=-4x2的图象的开口 ,对称轴是 ,顶点是_____ 顶点是抛物线的最____点
1.函数y=2x2的图象的开口 ,对称轴是 ,顶点是 ;
向上
向下
y轴
y轴
(0,0)
(0,0)
4.函数y= -0.3x2的图象的开口 ,对称轴是__ _,顶点是 ;
向上
y轴
(0,0)
向下
(0,0)
高
低
自主练习
y轴
5.下列说法正确的是( )
A.在函数y=2x2中,当x=0时,y有最大值0;
B.在函数y=2x2中当x>0时,y随x的增大而减小
C.抛物线y=2x2,y=-x2,y=-0.5x2中,抛物线y=2x2的开口最小
D.不论a取何值时,y=ax2的顶点都是原点
C
自主练习
A.(4,4) B.(1,-4)
C.(2,0) D.(0,4)
6.(哈尔滨·中考)在抛物线
上的一个点是( )
【答案】选C.
自主练习
7. 若点(x1,y1),B(x2,y2)是二次函数y=-3x2图象上的两点,且x1>x2>0,那么y1与y2的大小关系是_____________.
y2>y1
自主练习
课堂小结
一、重点学习了二次函数y=±x2的图象与性质
1.顶点坐标与对称轴.
2.位置与开口方向.
3.增减性与最值.
y=x2
y=-x2
二、拓展研究了二次函数y=ax2的图象与性质
三、依据a的正负,掌握从以下三个主要方面来研究二次函数的图象性质
生活中的二次函数
1.某一物体的质量为m,它运动飞约能量E与它的运动速度v之间的关系是∶
E=mv2(m为定值).
2.导线的电组为R,兰导线中有三流通过时,单位时间所产生的热量Q与电流强度1之间的关系是∶②Q=Rr2(R为定值).
3.g表示重力加速度,当物体自庄下落时,下落的距离h与下落时间t 之间的关系是∶h=gt2(g为定值).
§2.2 y=ax2的图象与性质
北师版九年级下册 二次函数
学习目标
1.经历探索二次函数图象的画法和性质的过程,获得利用图象研究函数性质的经验.(重点)
2.能够利用描点法作出y=x2的图象,并能根据图象认识和理解二次函数y=x2的性质.;(重点)
3.根据作出的二次函数y=-x2与y=x2的图象的异同比较,初步建立二次函数表达式与图象间的联系.理解表达式中,系数对图象的影响.(难点)
1.二次函数的定义
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.
(1)列表.
(3)连线.
(2)描点.
2.画函数图象的主要步骤是什么?
温 故 知 新
二次函数y=x2的图象与性质
观察y=x 的表达式,选择适当的x值,并计算相应的y值,完成下表∶
x -3 -2 --1 0 1 2 3
y 0
探究
1
1
4
4
9
9
1.列表
x
y
O
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
y=x2
2.描点
3.连线
2)在直角坐标系中描点.(3)用光滑的曲线连接各点,便得到函数y=x2的图象。
对于二次函数y=x2的图象,
(1)你能描述图象的形状吗
与同伴进行交流.
(2)图象与x轴有交点吗
如果有,交点坐标是什么
议一议
二次函数y=x2的图象与性质
二次函数y=x2的图象与性质
交流:
一、图像名称: .
二、图象开口向: .
三、图象对称性: .
四、图象的顶点(最低点)是 .
五、图形的增减性 .
六、y的最值 .
抛物线
向上
关于y轴轴对称
(0,0)
左减右增
y有最小值0
二次函数y=x 的图象是一条抛物线(parabola).它的
开口向上,且关于y轴对称。对称轴与抛物线的交点是抛物线的顶点、它是图象的最低点.
二次函数y=x2的图象与性质
总结:
二次函数y=-x2的图象是什么形状 先想一想,然后画出它的图象.它与 二次函数y=x2的图象有什么关系 与同伴进行交流。
二次函数y=-x2的图象与性质
探究
1、列表;
2、描点;
3、连线.
关于y=x2与y=-x2的相同与不同点。
二者相同点:(1)均为抛物线;(2)图象过原点;(3)均关于y轴对称.
二者不同点:(1)开口方向; (2)增减性;(3)y有最大(小)值
交流:
交流:
关于y=ax2的图象与性质。
a=1
(a>0)
开口
向上
关于
y轴对称
左减右增
a=-1
(a<0)
开口
向下
关于
y轴对称
左增右减
※二次项系数a对图像的影响:(1)开口方向;(2)增减性.
y=x2
y=-x2
观察y=2x2,y=-
议一议
的图象,并说一说你有什么发现?
通过对比观察,可以初步推断
二次函数y=ax2(a为不等于0的任意实数):
当a>0时,图象、性质与a=1时大致相同;
当a<0时,图象、性质与a=-1时大致相同.
唯一不同的地方,就是开口的大小。
二次项系数a对图象的影响:
1、图象的开口方向
探究:
a>0,图象开口向上.
a<0,图象开口向下.
2、y与x的增减性
a>0,左减右增.
a<0,左增右减.
3、开口大小
当a>0时,
a的绝对值越大,开口越小.
发现:
当a<0时,
a的绝对值越大,开口越小.
综合归纳
二次项系数a对图象的影响:
a>0
a<0
开口向上
开口向下
左减右增
左增右减
y有最小值0
y有最大值0
值越大,
口越小
把图中图象的号码,填在它的函数式后面:(填序号)
(1)y=3x2的图象是_______;
(2)y= x2的图象是_______;
(3)y=-x2的图象是_______;
(4)y= x2的图象是_______.
变式训练
③
①
④
②
3.函数y= x2的图象的开口 ,对称轴是 ,顶点是 ;顶点是抛物线的最____点.
2.函数y=-4x2的图象的开口 ,对称轴是 ,顶点是_____ 顶点是抛物线的最____点
1.函数y=2x2的图象的开口 ,对称轴是 ,顶点是 ;
向上
向下
y轴
y轴
(0,0)
(0,0)
4.函数y= -0.3x2的图象的开口 ,对称轴是__ _,顶点是 ;
向上
y轴
(0,0)
向下
(0,0)
高
低
自主练习
y轴
5.下列说法正确的是( )
A.在函数y=2x2中,当x=0时,y有最大值0;
B.在函数y=2x2中当x>0时,y随x的增大而减小
C.抛物线y=2x2,y=-x2,y=-0.5x2中,抛物线y=2x2的开口最小
D.不论a取何值时,y=ax2的顶点都是原点
C
自主练习
A.(4,4) B.(1,-4)
C.(2,0) D.(0,4)
6.(哈尔滨·中考)在抛物线
上的一个点是( )
【答案】选C.
自主练习
7. 若点(x1,y1),B(x2,y2)是二次函数y=-3x2图象上的两点,且x1>x2>0,那么y1与y2的大小关系是_____________.
y2>y1
自主练习
课堂小结
一、重点学习了二次函数y=±x2的图象与性质
1.顶点坐标与对称轴.
2.位置与开口方向.
3.增减性与最值.
y=x2
y=-x2
二、拓展研究了二次函数y=ax2的图象与性质
三、依据a的正负,掌握从以下三个主要方面来研究二次函数的图象性质
生活中的二次函数
1.某一物体的质量为m,它运动飞约能量E与它的运动速度v之间的关系是∶
E=mv2(m为定值).
2.导线的电组为R,兰导线中有三流通过时,单位时间所产生的热量Q与电流强度1之间的关系是∶②Q=Rr2(R为定值).
3.g表示重力加速度,当物体自庄下落时,下落的距离h与下落时间t 之间的关系是∶h=gt2(g为定值).
