5.2.3 求解一元一次方程 课件(共24张PPT)
文档属性
| 名称 | 5.2.3 求解一元一次方程 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 75.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
§5.2.3 求解一元一次方程
——含分母的方程
北师版七年级上册 一元一次方程
学习目标:
1.掌握含分母的一元一次方程的解法.
2.解一元一次方程的一般步骤.
请完成以下计算
温故知新
(1)12(2-3x)=4x+4
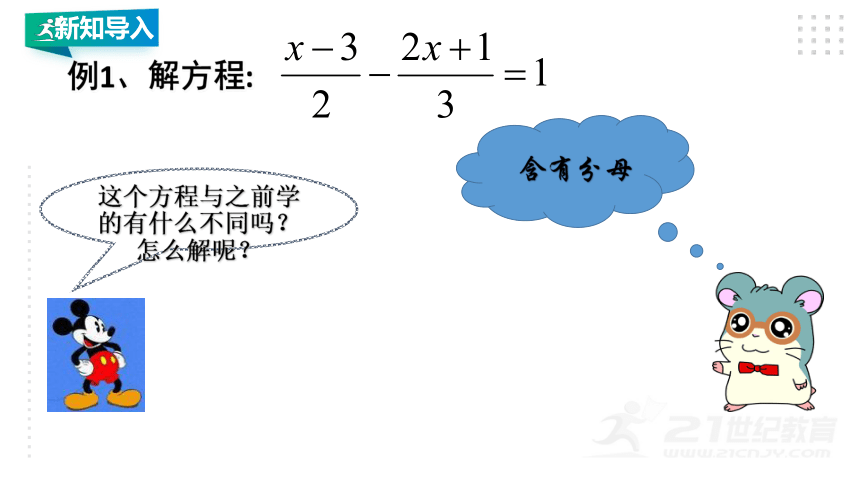
例1、解方程:
这个方程与之前学的有什么不同吗?怎么解呢?
含有分母
新知导入
解方程
3(x-3)-2(2x+1)=6,
3
2
去括号得
3x-9-4x-2=6,
合并同类项得
-x-11=6,
移项得
系数化为1得
x=-17,
解 去分母得
-x=17,
乘各分母的最小公倍数
新知讲解
解 去分母得
乘各分母的最小公倍数
其余过程同于上例
新知讲解
k取何值时,代数式 的值比 的值小1?
解:由题意得
新知讲解
其余过程同于上例
课堂小结
1、去分母
(方程两边乘各分母的最小公倍数)
2、去括号(注意变号)
3、移项(未知项左,常数项右)
4、合并同类项
5、系数化为1。
下面解方程的过程是否正确?不正确的请改正。
(1)
两边同乘以6,得 :10x-2=x+2- 6
(2)
去分母,得: 2(x-1)-3(5x+1)=1
(3)
去分母,得 4(2x+3)-9x+5=0
火眼金睛
1、去分母时,应在方程的左右两边乘以分母的 ;
2、去分母的依据是 ,去分母时不能漏乘 ;
3、去分母后,当分子为多项时,应将 。
分
母
注
意
最小公倍数
等式性质二
没有分母的项
该分子添上括号
去
(1)解方程:
解: 15x-5=8x+4-1,
15x-8x=4-1+5,
7x=8
火眼金睛
(2)解方程:
解: 2x-2-x+2=12-3x
2x-x+3x=12+2+2
4x=16
x=4.
火眼金睛
(二)
温故知新
解:去分母得
3
2
18x+3(x-1)=18-2(2x-1)
温故知新
请用分数的运算性质填空
10
200
分子、分母扩大10倍
分子、分母扩大100倍
分数的基本性质
分数的分子、分母同时乘以或除以同一个不为0的数,分数的值不变。
即:
=
=
(其中m≠0)
解方程
解:方程可化为
去分母,得
6(9x+2)-14(3+2x)-21(3x+14) = 42,
去括号,得
54x + 12-42-28x-63x-294 = 42,
合并同类项,得
新知讲解
解方程
解 原方程可化为
,
小数化分数
去分母,得
3(4x+21)-5(50-20x) = 9,
去括号,得
自主探究,合作交流
其余过程同于前例
小组PK赛
完成课本P139 “随堂练习”
方式:每两个小组合作,展开小组间对抗赛。
以优胜者加“积分”的方式进行奖励。
=1.6
—
(1)
(2)
;
课堂训练备选
(3)
(2)
(3)
课堂小结
(1)怎样去分母?
应在方程的左右两边都乘以各分母的最小公倍数。
(2)去分母的依据是什么? 等式性质2
(3)去分母的注意点是什么?
1、去分母时等式两边各项都要乘以最小公倍数,不可以漏乘。
2、如果分子是含有未知数的代数式,其作为一个整体应加括号。
(4)解一元一次方程的一般步骤是什么?
1.去分母 →2.去括号→ 3.移项→ 4.合并同类项 → 5.系数化为1
§5.2.3 求解一元一次方程
——含分母的方程
北师版七年级上册 一元一次方程
学习目标:
1.掌握含分母的一元一次方程的解法.
2.解一元一次方程的一般步骤.
请完成以下计算
温故知新
(1)12(2-3x)=4x+4
例1、解方程:
这个方程与之前学的有什么不同吗?怎么解呢?
含有分母
新知导入
解方程
3(x-3)-2(2x+1)=6,
3
2
去括号得
3x-9-4x-2=6,
合并同类项得
-x-11=6,
移项得
系数化为1得
x=-17,
解 去分母得
-x=17,
乘各分母的最小公倍数
新知讲解
解 去分母得
乘各分母的最小公倍数
其余过程同于上例
新知讲解
k取何值时,代数式 的值比 的值小1?
解:由题意得
新知讲解
其余过程同于上例
课堂小结
1、去分母
(方程两边乘各分母的最小公倍数)
2、去括号(注意变号)
3、移项(未知项左,常数项右)
4、合并同类项
5、系数化为1。
下面解方程的过程是否正确?不正确的请改正。
(1)
两边同乘以6,得 :10x-2=x+2- 6
(2)
去分母,得: 2(x-1)-3(5x+1)=1
(3)
去分母,得 4(2x+3)-9x+5=0
火眼金睛
1、去分母时,应在方程的左右两边乘以分母的 ;
2、去分母的依据是 ,去分母时不能漏乘 ;
3、去分母后,当分子为多项时,应将 。
分
母
注
意
最小公倍数
等式性质二
没有分母的项
该分子添上括号
去
(1)解方程:
解: 15x-5=8x+4-1,
15x-8x=4-1+5,
7x=8
火眼金睛
(2)解方程:
解: 2x-2-x+2=12-3x
2x-x+3x=12+2+2
4x=16
x=4.
火眼金睛
(二)
温故知新
解:去分母得
3
2
18x+3(x-1)=18-2(2x-1)
温故知新
请用分数的运算性质填空
10
200
分子、分母扩大10倍
分子、分母扩大100倍
分数的基本性质
分数的分子、分母同时乘以或除以同一个不为0的数,分数的值不变。
即:
=
=
(其中m≠0)
解方程
解:方程可化为
去分母,得
6(9x+2)-14(3+2x)-21(3x+14) = 42,
去括号,得
54x + 12-42-28x-63x-294 = 42,
合并同类项,得
新知讲解
解方程
解 原方程可化为
,
小数化分数
去分母,得
3(4x+21)-5(50-20x) = 9,
去括号,得
自主探究,合作交流
其余过程同于前例
小组PK赛
完成课本P139 “随堂练习”
方式:每两个小组合作,展开小组间对抗赛。
以优胜者加“积分”的方式进行奖励。
=1.6
—
(1)
(2)
;
课堂训练备选
(3)
(2)
(3)
课堂小结
(1)怎样去分母?
应在方程的左右两边都乘以各分母的最小公倍数。
(2)去分母的依据是什么? 等式性质2
(3)去分母的注意点是什么?
1、去分母时等式两边各项都要乘以最小公倍数,不可以漏乘。
2、如果分子是含有未知数的代数式,其作为一个整体应加括号。
(4)解一元一次方程的一般步骤是什么?
1.去分母 →2.去括号→ 3.移项→ 4.合并同类项 → 5.系数化为1
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
