4 三位数乘两位数-积的变化规律-四年级上册数学-人教版(共57张PPT)
文档属性
| 名称 | 4 三位数乘两位数-积的变化规律-四年级上册数学-人教版(共57张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 09:09:51 | ||
图片预览


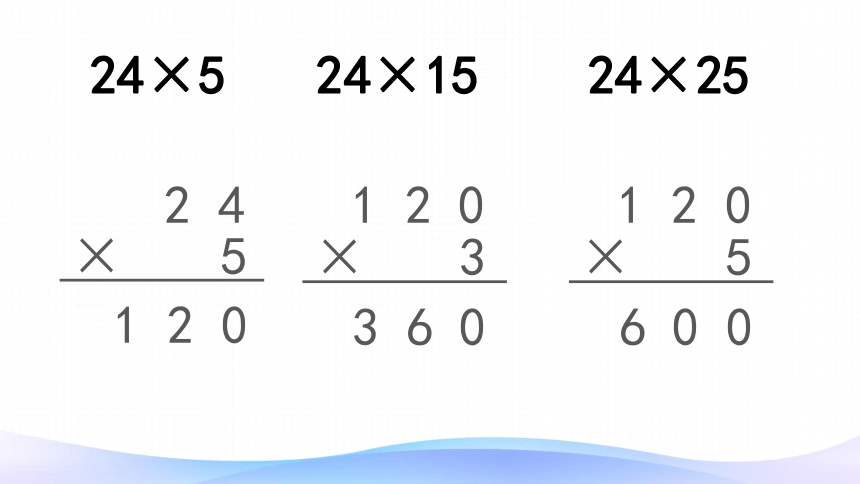








文档简介
(共57张PPT)
三位数
乘两位数
积的变化规律
24×5
24×15
24×25
计算以下算式
24×5
24×15
24×25
2 4
5
×
1 2 0
1 2 0
3
×
3 6 0
1 2 0
5
×
6 0 0
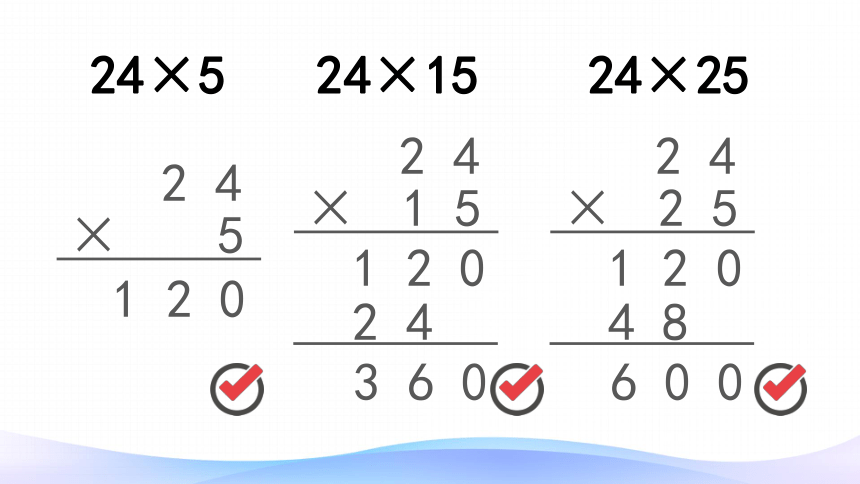
24×5
24×15
24×25
2 4
5
×
1 2 0
2 4
1 5
×
1 2 0
2 4
3 6 0
2 4
2 5
×
1 2 0
4 8
6 0 0
24×5
24×15
24×25
2 4
5
×
1 2 0
1 2 0
3
×
3 6 0
1 2 0
5
×
6 0 0
15是5的3倍
25是5的5倍
乘法运算
乘法的关系式:
因数乘因数等于积。
第一组: 第二组:
8×2=( ) 80×4=( )
8×20=( ) 40×4=( )
8×200=( ) 20×4=( )
比较每组的3个算式,因数与积有什么变化?
第一组: 第二组:
8×2=( ) 80×4=( )
8×20=( ) 40×4=( )
8×200=( ) 20×4=( )
第一组: 第二组:
8×2=( ) 80×4=( )
8×20=( ) 40×4=( )
8×200=( ) 20×4=( )
16
160
1600
320
160
80
比较每组的3个算式,因数与积有什么变化?
8×2=( )
8×20=( )
8×200=( )
8不变,一个因数乘10,积也乘10。
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
×10
×10
×10
×10
一个因数不变,另一个因数乘10,积也乘10。
16
160
1600
8×2=( )
8×20=( )
8×200=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
×10
×10
×10
×10
8不变,一个因数乘10,积也乘10。
16
160
1600
8×2=( )
8×20=( )
8×200=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
16
160
1600
×100
×100
它们的变化趋势一直在逐渐地变大。
8×2=( )
8×20=( )
8×200=( )
第1组算式里,谁没变?谁变了?
16
160
1600
第一个因数不变。
第一个因数不变,第二个因数变化,积也随着因数的变化而变化。
乘0是不行的。
因为任何数乘0,都得0。
第一个因数不变,第二个因数乘几,积也乘几。
另一个因数乘10,乘100(0除外)。
8×2=( )
8×20=( )
8×200=( )
第1组算式里,谁没变?谁变了?
16
160
1600
第一个因数不变。
×10
×10
×100
×100
另一个因数乘10,乘100,只能像这样,乘整数吗?
8×600=( )
除了0不可以,除了整十整百这样的整数,还有什么数是可以的?
除0以外的任何数。
8×2=( )
8×20=( )
8×200=( )
16
160
1600
4800
一个因数不变,第二个因数乘3,积也乘3。
×3
8×1600=( )
除了0不可以,除了整十整百这样的整数,还有什么数是可以的?
8×2=( )
8×20=( )
8×200=( )
16
160
1600
×8
除0以外的任何数。
8×3600=( )
除了0不可以,除了整十整百这样的整数,还有什么数是可以的?
8×2=( )
8×20=( )
8×200=( )
16
160
1600
×18
除0以外的任何数。
8×17600=( )
除了0不可以,除了整十整百这样的整数,还有什么数是可以的?
8×2=( )
8×20=( )
8×200=( )
16
160
1600
×88
除0以外的任何数。
一个因数不变,另一个因数乘几(0除外),积也乘几。
一个因数不变,另一个因数乘几(0除外),积也乘几。
除了0不可以,除了整十整百这样的整数,还有什么数是可以的?
8×2=( )
8×20=( )
8×200=( )
16
160
1600
除0以外的任何数。
80×4=( )
40×4=( )
20×4=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
320
160
80
÷2
÷2
÷2
÷2
÷4
÷4
80×4=( )
40×4=( )
20×4=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
320
160
80
÷2
÷2
÷2
÷2
÷4
÷4
80×4=( )
40×4=( )
20×4=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
320
160
80
0在这个算式里是要除外的。
因为0不能做除数,所以它是不成立的。
如果发现了规律的话,一定要加上一个(0除外)。
你真棒!
80×4=( )
40×4=( )
20×4=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
320
160
80
积随着第一个因数,在逐渐地变小。
80×4=( )
40×4=( )
20×4=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
320
160
80
第一个因数变化,第二个因数没有变化,积变化了。
一个因数不变,另一个因数乘或除以几(0除外)。
一个因数不变,另一个因数乘或除以几(0除外),积也乘或除以几。
一个因数不变,另一个因数除以几,积也除以几。
80×4=( )
40×4=( )
比较第一个和第二个算式,因数与积有什么变化?你发现了什么?
320
160
一个因数不变,另一个因数除以几。
0除外。
因为0不能做除数。
一个因数不变,另一个因数乘(或除以)几(0除外),积也乘(或除以)几。
积的变化规律
要求:每位学生写一组算式,一组3个,展现积分别随一个因数扩大或缩小的变化情况。
要求:每位学生写一组算式,一组3个,展现积分别随一个因数扩大或缩小的变化情况。
举例说明你发现的规律
2×3=6
2×30=60
2×300=600
×10
×10
×10
×10
2×3=6
2×30=60
2×300=600
×100
×100
2×9=18
4×9=36
8×9=72
×2
×2
×2
×2
乘2或者乘4
2×9=18
4×9=36
8×9=72
2×3=6
2×30=60
2×300=600
不是用整数来变化的
用整数来变化的
乘整十整百
100×3=300
50×3=150
25×3=75
÷2
÷2
÷2
÷2
100×3=300
50×3=150
25×3=75
÷4
÷4
100×3=300
50×3=150
25×3=75
2×9=18
4×9=36
8×9=72
积越变越大
积越变越小
第一个因数也越变越大
第一个因数也越变越小
积也随着因数的变化而变化
7×3=21
70×3=210
700×3=2100
80÷4=20
40÷4=10
20÷4=5
除法算式
因数乘因数等于积
商的变化规律
×10
×10
×10
×10
7×3=21
70×3=210
700×3=2100
80÷4=20
40÷4=10
20÷4=5
因数乘因数等于积
×100
×100
商的变化规律
24×5=120
24×50=
240×50=
26×48=1248
26×24=
26×12=
根据第一题的积,直接写出下面两题的得数。
计算大比拼
24×5=120
24×50=
240×50=
1200
根据第一题的积,直接写出下面两题的得数。
计算大比拼
×10
×10
×10
×10
12000
计算大比拼
×10
×10
×100
根据第一题的积,直接写出下面两题的得数。
24×5=120
24×50=
240×50=
12000
1200
26×48=1248
26×24=
26×12=
624
312
计算大比拼
根据第一题的积,直接写出下面两题的得数。
÷2
÷2
÷2
÷2
选择一题计算出得数,根据积的变化规律直接写出其它题的得数。
选择一题计算出得数,根据积的变化规律直接写出其它题的得数。
46×50=
46×100=
4600
46×150=
6900
46×200=
9200
2300
×3
×3
×2
×2
÷2
÷2
选择一题计算出得数,根据积的变化规律直接写出其它题的得数。
460×20=
46×200=
9200
9200
×10
÷10
选择一题计算出得数,根据积的变化规律直接写出其它题的得数。
460×20=
46×200=
9200
9200
×10
÷10
5元3千克
10元2千克
6千克苹果应付( )元。
4千克香蕉应付( )元。
妈妈应付( )元。
妈妈打算买6千克苹果和4千克香蕉。
图片素材来源网络,如有侵权请联系我们!
5元3千克
10元2千克
6千克苹果应付( )元。
10
妈妈打算买6千克苹果和4千克香蕉。
=10(元)
5×2
=2
6÷3
( )
( )×3=5(元)
10(元)
×2
×2
( )×6=
图片素材来源网络,如有侵权请联系我们!
5元3千克
10元2千克
6千克苹果应付( )元。
4千克香蕉应付( )元。
10
20
妈妈打算买6千克苹果和4千克香蕉。
4千克香蕉,等于2千克10元香蕉的两倍,等于10元乘2。
=20(元)
2×10
4÷2=2
图片素材来源网络,如有侵权请联系我们!
5元3千克
10元2千克
6千克苹果应付( )元。
4千克香蕉应付( )元。
妈妈应付( )元。
10
20
30
妈妈打算买6千克苹果和4千克香蕉。
图片素材来源网络,如有侵权请联系我们!
一块长方形的绿地面积是256平方米,现做如下改造:
(1)长不变,宽增加到12米。现绿地面积是多少?
(2)如果长除以4,宽乘4。现绿地面积是多少?
4米
256平方米
一块长方形的绿地面积是256平方米,现做如下改造:
(1)长不变,宽增加到12米。现绿地面积是多少?
4米
256平方米
S长方形=长×宽
256÷4
=64m
64×12
=768m2
12÷4
=3
256×3
=768m2
64×12
=768m2
64×4
=256m2
×3
×3
一块长方形的绿地面积是256平方米,现做如下改造:
(1)长不变,宽增加到12米。现绿地面积是多少?
4米
256平方米
12÷4
=3
256×3
=768m2
现在扩大了到它的三倍,有三个256m2。
4米
256平方米
4米
256平方米
4米
256平方米
一块长方形的绿地面积是256平方米,现做如下改造:
(1)长不变,宽增加到12米。现绿地面积是多少?
长没变化
面积扩大了三倍
256×3=768(m2)
4米
256平方米
4米
256平方米
4米
256平方米
一块长方形的绿地面积是256平方米,现做如下改造:
(1)长不变,宽增加到12米。现绿地面积是多少?
长不变
宽×3
面积×3
一块长方形的绿地面积是256平方米,现做如下改造:
(2)如果长除以4,宽乘4。现绿地面积是多少?
4米
256平方米
256÷4×4
=256m2
利用积的变化规律,长除以4,宽乘4,积不变,面积不变。
积的变化规律,可以使我们的计算简便,也可以给生活带来简便。
积的变化规律运用到生活,会更简便一些。
积的变化规律。
商的变化规律。
再见!
三位数
乘两位数
积的变化规律
24×5
24×15
24×25
计算以下算式
24×5
24×15
24×25
2 4
5
×
1 2 0
1 2 0
3
×
3 6 0
1 2 0
5
×
6 0 0
24×5
24×15
24×25
2 4
5
×
1 2 0
2 4
1 5
×
1 2 0
2 4
3 6 0
2 4
2 5
×
1 2 0
4 8
6 0 0
24×5
24×15
24×25
2 4
5
×
1 2 0
1 2 0
3
×
3 6 0
1 2 0
5
×
6 0 0
15是5的3倍
25是5的5倍
乘法运算
乘法的关系式:
因数乘因数等于积。
第一组: 第二组:
8×2=( ) 80×4=( )
8×20=( ) 40×4=( )
8×200=( ) 20×4=( )
比较每组的3个算式,因数与积有什么变化?
第一组: 第二组:
8×2=( ) 80×4=( )
8×20=( ) 40×4=( )
8×200=( ) 20×4=( )
第一组: 第二组:
8×2=( ) 80×4=( )
8×20=( ) 40×4=( )
8×200=( ) 20×4=( )
16
160
1600
320
160
80
比较每组的3个算式,因数与积有什么变化?
8×2=( )
8×20=( )
8×200=( )
8不变,一个因数乘10,积也乘10。
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
×10
×10
×10
×10
一个因数不变,另一个因数乘10,积也乘10。
16
160
1600
8×2=( )
8×20=( )
8×200=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
×10
×10
×10
×10
8不变,一个因数乘10,积也乘10。
16
160
1600
8×2=( )
8×20=( )
8×200=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
16
160
1600
×100
×100
它们的变化趋势一直在逐渐地变大。
8×2=( )
8×20=( )
8×200=( )
第1组算式里,谁没变?谁变了?
16
160
1600
第一个因数不变。
第一个因数不变,第二个因数变化,积也随着因数的变化而变化。
乘0是不行的。
因为任何数乘0,都得0。
第一个因数不变,第二个因数乘几,积也乘几。
另一个因数乘10,乘100(0除外)。
8×2=( )
8×20=( )
8×200=( )
第1组算式里,谁没变?谁变了?
16
160
1600
第一个因数不变。
×10
×10
×100
×100
另一个因数乘10,乘100,只能像这样,乘整数吗?
8×600=( )
除了0不可以,除了整十整百这样的整数,还有什么数是可以的?
除0以外的任何数。
8×2=( )
8×20=( )
8×200=( )
16
160
1600
4800
一个因数不变,第二个因数乘3,积也乘3。
×3
8×1600=( )
除了0不可以,除了整十整百这样的整数,还有什么数是可以的?
8×2=( )
8×20=( )
8×200=( )
16
160
1600
×8
除0以外的任何数。
8×3600=( )
除了0不可以,除了整十整百这样的整数,还有什么数是可以的?
8×2=( )
8×20=( )
8×200=( )
16
160
1600
×18
除0以外的任何数。
8×17600=( )
除了0不可以,除了整十整百这样的整数,还有什么数是可以的?
8×2=( )
8×20=( )
8×200=( )
16
160
1600
×88
除0以外的任何数。
一个因数不变,另一个因数乘几(0除外),积也乘几。
一个因数不变,另一个因数乘几(0除外),积也乘几。
除了0不可以,除了整十整百这样的整数,还有什么数是可以的?
8×2=( )
8×20=( )
8×200=( )
16
160
1600
除0以外的任何数。
80×4=( )
40×4=( )
20×4=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
320
160
80
÷2
÷2
÷2
÷2
÷4
÷4
80×4=( )
40×4=( )
20×4=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
320
160
80
÷2
÷2
÷2
÷2
÷4
÷4
80×4=( )
40×4=( )
20×4=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
320
160
80
0在这个算式里是要除外的。
因为0不能做除数,所以它是不成立的。
如果发现了规律的话,一定要加上一个(0除外)。
你真棒!
80×4=( )
40×4=( )
20×4=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
320
160
80
积随着第一个因数,在逐渐地变小。
80×4=( )
40×4=( )
20×4=( )
比较每组的3个算式,因数与积有什么变化?
你发现了什么?
320
160
80
第一个因数变化,第二个因数没有变化,积变化了。
一个因数不变,另一个因数乘或除以几(0除外)。
一个因数不变,另一个因数乘或除以几(0除外),积也乘或除以几。
一个因数不变,另一个因数除以几,积也除以几。
80×4=( )
40×4=( )
比较第一个和第二个算式,因数与积有什么变化?你发现了什么?
320
160
一个因数不变,另一个因数除以几。
0除外。
因为0不能做除数。
一个因数不变,另一个因数乘(或除以)几(0除外),积也乘(或除以)几。
积的变化规律
要求:每位学生写一组算式,一组3个,展现积分别随一个因数扩大或缩小的变化情况。
要求:每位学生写一组算式,一组3个,展现积分别随一个因数扩大或缩小的变化情况。
举例说明你发现的规律
2×3=6
2×30=60
2×300=600
×10
×10
×10
×10
2×3=6
2×30=60
2×300=600
×100
×100
2×9=18
4×9=36
8×9=72
×2
×2
×2
×2
乘2或者乘4
2×9=18
4×9=36
8×9=72
2×3=6
2×30=60
2×300=600
不是用整数来变化的
用整数来变化的
乘整十整百
100×3=300
50×3=150
25×3=75
÷2
÷2
÷2
÷2
100×3=300
50×3=150
25×3=75
÷4
÷4
100×3=300
50×3=150
25×3=75
2×9=18
4×9=36
8×9=72
积越变越大
积越变越小
第一个因数也越变越大
第一个因数也越变越小
积也随着因数的变化而变化
7×3=21
70×3=210
700×3=2100
80÷4=20
40÷4=10
20÷4=5
除法算式
因数乘因数等于积
商的变化规律
×10
×10
×10
×10
7×3=21
70×3=210
700×3=2100
80÷4=20
40÷4=10
20÷4=5
因数乘因数等于积
×100
×100
商的变化规律
24×5=120
24×50=
240×50=
26×48=1248
26×24=
26×12=
根据第一题的积,直接写出下面两题的得数。
计算大比拼
24×5=120
24×50=
240×50=
1200
根据第一题的积,直接写出下面两题的得数。
计算大比拼
×10
×10
×10
×10
12000
计算大比拼
×10
×10
×100
根据第一题的积,直接写出下面两题的得数。
24×5=120
24×50=
240×50=
12000
1200
26×48=1248
26×24=
26×12=
624
312
计算大比拼
根据第一题的积,直接写出下面两题的得数。
÷2
÷2
÷2
÷2
选择一题计算出得数,根据积的变化规律直接写出其它题的得数。
选择一题计算出得数,根据积的变化规律直接写出其它题的得数。
46×50=
46×100=
4600
46×150=
6900
46×200=
9200
2300
×3
×3
×2
×2
÷2
÷2
选择一题计算出得数,根据积的变化规律直接写出其它题的得数。
460×20=
46×200=
9200
9200
×10
÷10
选择一题计算出得数,根据积的变化规律直接写出其它题的得数。
460×20=
46×200=
9200
9200
×10
÷10
5元3千克
10元2千克
6千克苹果应付( )元。
4千克香蕉应付( )元。
妈妈应付( )元。
妈妈打算买6千克苹果和4千克香蕉。
图片素材来源网络,如有侵权请联系我们!
5元3千克
10元2千克
6千克苹果应付( )元。
10
妈妈打算买6千克苹果和4千克香蕉。
=10(元)
5×2
=2
6÷3
( )
( )×3=5(元)
10(元)
×2
×2
( )×6=
图片素材来源网络,如有侵权请联系我们!
5元3千克
10元2千克
6千克苹果应付( )元。
4千克香蕉应付( )元。
10
20
妈妈打算买6千克苹果和4千克香蕉。
4千克香蕉,等于2千克10元香蕉的两倍,等于10元乘2。
=20(元)
2×10
4÷2=2
图片素材来源网络,如有侵权请联系我们!
5元3千克
10元2千克
6千克苹果应付( )元。
4千克香蕉应付( )元。
妈妈应付( )元。
10
20
30
妈妈打算买6千克苹果和4千克香蕉。
图片素材来源网络,如有侵权请联系我们!
一块长方形的绿地面积是256平方米,现做如下改造:
(1)长不变,宽增加到12米。现绿地面积是多少?
(2)如果长除以4,宽乘4。现绿地面积是多少?
4米
256平方米
一块长方形的绿地面积是256平方米,现做如下改造:
(1)长不变,宽增加到12米。现绿地面积是多少?
4米
256平方米
S长方形=长×宽
256÷4
=64m
64×12
=768m2
12÷4
=3
256×3
=768m2
64×12
=768m2
64×4
=256m2
×3
×3
一块长方形的绿地面积是256平方米,现做如下改造:
(1)长不变,宽增加到12米。现绿地面积是多少?
4米
256平方米
12÷4
=3
256×3
=768m2
现在扩大了到它的三倍,有三个256m2。
4米
256平方米
4米
256平方米
4米
256平方米
一块长方形的绿地面积是256平方米,现做如下改造:
(1)长不变,宽增加到12米。现绿地面积是多少?
长没变化
面积扩大了三倍
256×3=768(m2)
4米
256平方米
4米
256平方米
4米
256平方米
一块长方形的绿地面积是256平方米,现做如下改造:
(1)长不变,宽增加到12米。现绿地面积是多少?
长不变
宽×3
面积×3
一块长方形的绿地面积是256平方米,现做如下改造:
(2)如果长除以4,宽乘4。现绿地面积是多少?
4米
256平方米
256÷4×4
=256m2
利用积的变化规律,长除以4,宽乘4,积不变,面积不变。
积的变化规律,可以使我们的计算简便,也可以给生活带来简便。
积的变化规律运用到生活,会更简便一些。
积的变化规律。
商的变化规律。
再见!
