24.1 圆的有关性质 同步分层作业(含解析)
文档属性
| 名称 | 24.1 圆的有关性质 同步分层作业(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-11 08:17:10 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2021年数学人教新版九年级同步分层作业---圆的有关性质
一.选择题(共10小题)
1.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为( )
A.8 B.6 C.4 D.2
2.一个压路机的前轮直径是1.7米,如果前轮每分钟转动6周,那么这台压路机10分钟前进( )米.
A.51π B.102π C.153π D.204π
3.如图,⊙O的弦AB垂直平分半径OC,若弦AB=2,则⊙O的半径为( )
A. B. C. D.2
4.如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),下列不符合条件的OP的值是( )
A.4 B.3 C.3.5 D.2.5
5.计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
若圆半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.d(25%)=1
B.当x>50%时,d(x)>1
C.当x1>x2时,d(x1)>d(x2)
D.当x1+x2=100%时,d(x1)=d(x2)
6.如图,已知四边形ABCD内接于⊙O,∠A=100°,则∠BOD=( )
A.80° B.50° C.160° D.100°
7.如图,AB是半圆O的直径,点C,D在半圆O上.若∠ABC=50°,则∠BDC的度数为( )
A.90° B.100° C.130° D.140°
8.如图,A,B,C是⊙O上的三个点,若∠B=32°,则∠AOC=( )
A.64° B.58° C.68° D.55°
9.下列说法中一定正确的是( )
A.相等的圆心角所对的弧相等
B.圆上任意两点间的部分叫做圆弧
C.平分弦的直径垂直于弦
D.圆周角等于圆心角的一半
10.如图,已知BD是⊙O的直径,BD⊥AC于点E,∠AOC=100°,则∠BDC的度数是( )
A.20° B.25° C.30° D.40°
二.填空题(共10小题)
11.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D= 度.
12.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP长为整数时,P点有 个.
13.如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的半径为2cm,则此时M、N两点间的距离是 cm.
14.如图,AB是⊙O的直径,弦CD⊥AB于点E,且AE=CD=6,则⊙O的半径为 .
15.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,连结OC,若OC=5,AE=2,则CD= .
16.如图,点A、B、C、D、E在⊙O上,弧AB度数为30°,则∠E+∠C= .
17.如图,四边形ABCD内接于⊙O,∠A:∠B:∠C=7:4:2.则∠D= .
18.如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于 .
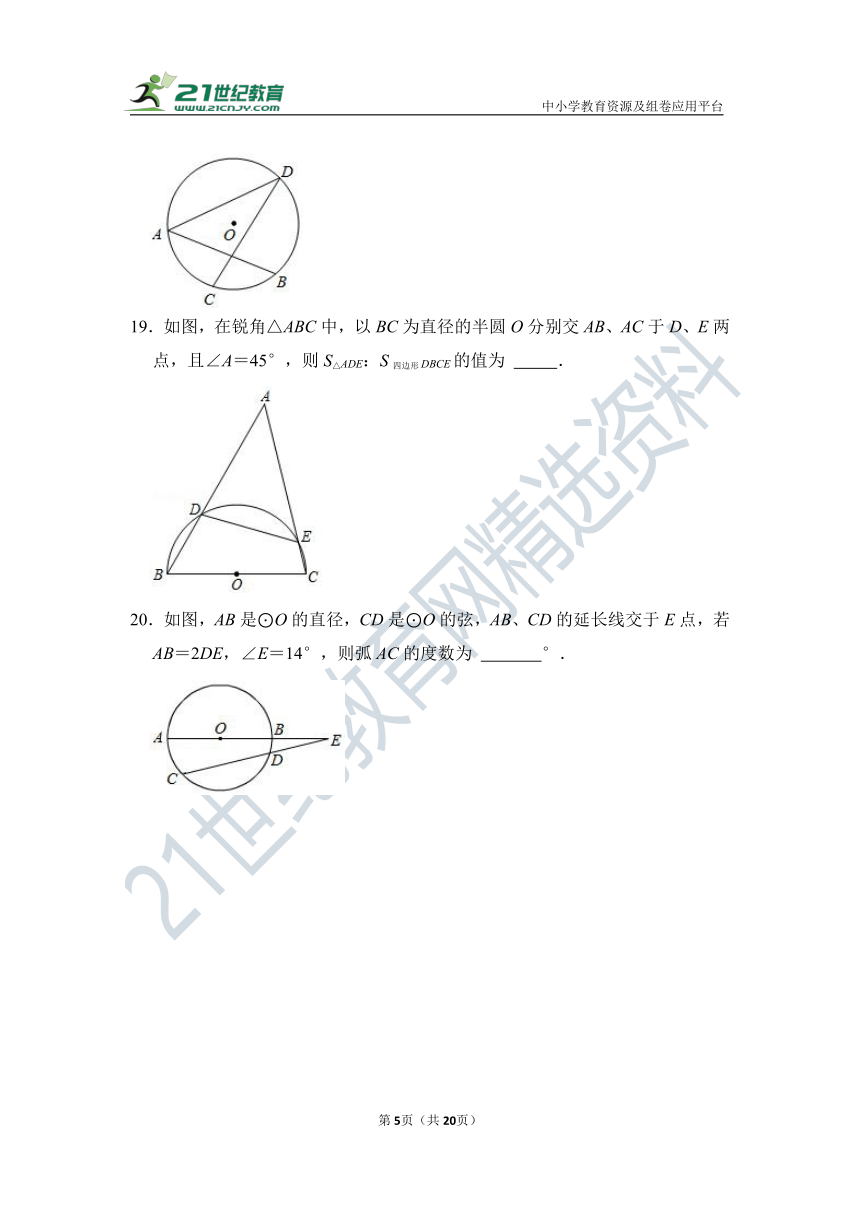
19.如图,在锐角△ABC中,以BC为直径的半圆O分别交AB、AC于D、E两点,且∠A=45°,则S△ADE:S四边形DBCE的值为 .
20.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,若AB=2DE,∠E=14°,则弧AC的度数为 °.
2021年数学人教新版九年级同步分层作业---圆的有关性质
参考答案与试题解析
一.选择题(共10小题)
1.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为( )
A.8 B.6 C.4 D.2
【解答】解:如图,连接OC.
∵四边形OBCD是矩形,
∴∠OBC=90°,BD=OC=OA=10,
∴OB===6,
∴AB=OA﹣OB=4,
故选:C.
2.一个压路机的前轮直径是1.7米,如果前轮每分钟转动6周,那么这台压路机10分钟前进( )米.
A.51π B.102π C.153π D.204π
【解答】解:前轮的底面圆周长:π×1.7=1.7π(米),1.7π×6×10=102π(米)
故选:B.
3.如图,⊙O的弦AB垂直平分半径OC,若弦AB=2,则⊙O的半径为( )
A. B. C. D.2
【解答】解:连接OA,设OA=OC=r.
∵弦AB垂直平分半径OC,
∴OE=OC=r,AE=BE=,
在Rt△AOE中,由勾股定理得:r2=(r)2+()2,
解得r=2或﹣2(舍弃).
故选:D.
4.如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),下列不符合条件的OP的值是( )
A.4 B.3 C.3.5 D.2.5
【解答】解:连接OB,作OM⊥AB于M.
∵OM⊥AB,
∴AM=BM=AB=4,
在直角△OBM中,∵OB=5,BM=4,
∴OM===3.
∴3≤OP<5,
故选:D.
5.计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
若圆半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.d(25%)=1
B.当x>50%时,d(x)>1
C.当x1>x2时,d(x1)>d(x2)
D.当x1+x2=100%时,d(x1)=d(x2)
【解答】解:A、d(25%)=>1,本选项不符合题意.
B、当x>50%时,0≤d(x)<2,本选项不符合题意.
C、当x1>x2时,d(x1)与d(x2)可能相等,可能不等,本选项不符合题意.
D、当x1+x2=100%时,d(x1)=d(x2),本选项符合题意.
故选:D.
6.如图,已知四边形ABCD内接于⊙O,∠A=100°,则∠BOD=( )
A.80° B.50° C.160° D.100°
【解答】解:∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°,
∵∠A=100°,
∴∠C=180°﹣∠A=180°﹣100°=80°,
由圆周角定理得:∠BOD=2∠C=160°,
故选:C.
7.如图,AB是半圆O的直径,点C,D在半圆O上.若∠ABC=50°,则∠BDC的度数为( )
A.90° B.100° C.130° D.140°
【解答】解:∵AB是半圆O的直径,
∴∠ACB=90°.
又∠ABC=50°,
∴∠A=40°,
∵四边形ABDC为圆O的内接四边形,
∴∠A+∠BDC=180°,
∴∠BDC=140°,
故选:D.
8.如图,A,B,C是⊙O上的三个点,若∠B=32°,则∠AOC=( )
A.64° B.58° C.68° D.55°
【解答】解:如图,∵∠B=32°,
∴∠AOC=2∠B=2×32°=64°.
故选:A.
9.下列说法中一定正确的是( )
A.相等的圆心角所对的弧相等
B.圆上任意两点间的部分叫做圆弧
C.平分弦的直径垂直于弦
D.圆周角等于圆心角的一半
【解答】解:同圆或等圆中,相等的圆心角所对的弧相等,故A说法错误;
圆上任意两点间的部分叫做圆弧,故B说法正确;
平分弦(不是直径)的直径垂直于弦,故C说法错误;
同圆或等圆中,同弧所对的圆周角等于圆心角的一半,故D说法错误.
故选:B.
10.如图,已知BD是⊙O的直径,BD⊥AC于点E,∠AOC=100°,则∠BDC的度数是( )
A.20° B.25° C.30° D.40°
【解答】解:∵BD⊥AC,∠AOC=100°,
∴∠BOC=∠AOC=50°,
则∠BDC=∠BOC=25°,
故选:B.
二.填空题(共10小题)
11.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D= 25 度.
【解答】解:连接OB,
∵BD=OA,OA=OB
所以△AOB和△BOD为等腰三角形,
设∠D=x度,则∠OBA=2x°,
因为OB=OA,
所以∠A=2x°,
在△AOB中,2x+2x+(105﹣x)=180,
解得x=25,
即∠D=25°.
12.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP长为整数时,P点有 4 个.
【解答】解:解法一:过O作OC⊥AB于C,则AC=BC,
设OC=x,AC=y,
∵AB是⊙O的一条弦,⊙O的半径为6,
∴AB≤12,
∵△OAB的面积为18,
∴,
则y=,
∴,
解得x=3或﹣3(舍),
∴OC=3>4,
∴4<OP≤6,
∵点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
解法二:设△AOB中OA边上的高为h,
则,即,
∴h=6,
∵OB=6,
∴OA⊥OB,即∠AOB=90°,
∴AB=6,图中OC=3,
同理得:点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
故答案为:4.
13.如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的半径为2cm,则此时M、N两点间的距离是 2 cm.
【解答】解:根据题意得:EF=BC,MN=EF,
把该正方形纸片卷成一个圆柱,使点A与点D重合,则线段BC形成一半径为2cm的圆,线段BC是圆的周长,
BC=EF=2π×2=4π,
∴的长=EF==,
∴n=120°,即∠MON=120°,
∵OM=ON,
∴∠M=30°,
过O作OG⊥MN于G,
∵OM=2,
∴OG=1,MG=,
∴MN=2MG=2,
故答案为:2.
14.如图,AB是⊙O的直径,弦CD⊥AB于点E,且AE=CD=6,则⊙O的半径为 .
【解答】解:∵CD⊥AB,
∴CE=DE=CD,
∵AE=CD=6,
∴CE=DE=3,
∵OD=OB=OA,OE=AE﹣OA,
在Rt△ODE中,由勾股定理可得:OD2=DE2+(AE﹣OA)2,
即:OD2=32+(6﹣OD)2,
解得:OD=,
∴⊙O的半径为:,
故答案为:.
15.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,连结OC,若OC=5,AE=2,则CD= 8 .
【解答】解:∵AB为圆O的直径,弦CD⊥AB,
∴CD=2CE,
∵OC=5,AE=2,
∴OA=5,
∴OE=OA﹣AE=5﹣2=3,
∴CE=.
∴CD=2CE=8.
故答案为:8.
16.如图,点A、B、C、D、E在⊙O上,弧AB度数为30°,则∠E+∠C= 165° .
【解答】解:连接EA,
∵弧AB度数为30°,
∴∠AEB=15°,
∵四边形ACDE为⊙O的内接四边形,
∴∠C+∠AED=180°,
∴∠C+∠BED=180°﹣15°=165°,
故答案为:165°.
17.如图,四边形ABCD内接于⊙O,∠A:∠B:∠C=7:4:2.则∠D= 100° .
【解答】解:设∠A=7x,则∠B=4x,∠C=2x,
∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,∠B+∠D=180°,
∴2x+7x=180°,解得x=20°,
∴∠D=180°﹣4x=180°﹣80°=100°.
故答案为100°.
18.如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于 .
【解答】解:如图,
连接OA、OC,OC交AB于点E,
∵点C是弧AB中点,AB=6,
∴OC⊥AB,且AE=BE=3,
∵∠ADC=30°,
∴∠AOC=2∠ADC=60°,
∴∠OAE=30°,
∴OE=AE tan30°=3×=,
故圆心O到弦AB的距离为.
故答案为:.
19.如图,在锐角△ABC中,以BC为直径的半圆O分别交AB、AC于D、E两点,且∠A=45°,则S△ADE:S四边形DBCE的值为 1 .
【解答】解:连接BE,如图所示:
∵BC是⊙O的直径,
∴∠BEC=90°,
∴∠AEB=180°﹣90°=90°,
在Rt△ABE中,∠A=45°,
∴cosA=cos45°==,
∵四边形DBCE内接于⊙O,
∴∠ADE=∠ACB,∠AED=∠ABC,
∴△ADE∽△ACB,
∴===,
S△ADE:S四边形DBCE的值为1,
故答案为:1.
20.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,若AB=2DE,∠E=14°,则弧AC的度数为 42 °.
【解答】解:如图,连接OC、OD,
∵AB=2DE,
∴OD=DE,
∴∠E=∠EOD=14°,
在△EDO中,∠ODC=∠E+∠EOD=28°,
∵OC=OD,
∴∠OCD=∠ODC=28°,
在△CEO中,∠AOC=∠E+∠OCD=14°+28°=42°,
∴弧AC的度数为42°.
故答案为:42°.
第1页(共1页)
2021年数学人教新版九年级同步分层作业---圆的有关性质
一.选择题(共10小题)
1.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为( )
A.8 B.6 C.4 D.2
2.一个压路机的前轮直径是1.7米,如果前轮每分钟转动6周,那么这台压路机10分钟前进( )米.
A.51π B.102π C.153π D.204π
3.如图,⊙O的弦AB垂直平分半径OC,若弦AB=2,则⊙O的半径为( )
A. B. C. D.2
4.如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),下列不符合条件的OP的值是( )
A.4 B.3 C.3.5 D.2.5
5.计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
若圆半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.d(25%)=1
B.当x>50%时,d(x)>1
C.当x1>x2时,d(x1)>d(x2)
D.当x1+x2=100%时,d(x1)=d(x2)
6.如图,已知四边形ABCD内接于⊙O,∠A=100°,则∠BOD=( )
A.80° B.50° C.160° D.100°
7.如图,AB是半圆O的直径,点C,D在半圆O上.若∠ABC=50°,则∠BDC的度数为( )
A.90° B.100° C.130° D.140°
8.如图,A,B,C是⊙O上的三个点,若∠B=32°,则∠AOC=( )
A.64° B.58° C.68° D.55°
9.下列说法中一定正确的是( )
A.相等的圆心角所对的弧相等
B.圆上任意两点间的部分叫做圆弧
C.平分弦的直径垂直于弦
D.圆周角等于圆心角的一半
10.如图,已知BD是⊙O的直径,BD⊥AC于点E,∠AOC=100°,则∠BDC的度数是( )
A.20° B.25° C.30° D.40°
二.填空题(共10小题)
11.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D= 度.
12.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP长为整数时,P点有 个.
13.如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的半径为2cm,则此时M、N两点间的距离是 cm.
14.如图,AB是⊙O的直径,弦CD⊥AB于点E,且AE=CD=6,则⊙O的半径为 .
15.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,连结OC,若OC=5,AE=2,则CD= .
16.如图,点A、B、C、D、E在⊙O上,弧AB度数为30°,则∠E+∠C= .
17.如图,四边形ABCD内接于⊙O,∠A:∠B:∠C=7:4:2.则∠D= .
18.如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于 .
19.如图,在锐角△ABC中,以BC为直径的半圆O分别交AB、AC于D、E两点,且∠A=45°,则S△ADE:S四边形DBCE的值为 .
20.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,若AB=2DE,∠E=14°,则弧AC的度数为 °.
2021年数学人教新版九年级同步分层作业---圆的有关性质
参考答案与试题解析
一.选择题(共10小题)
1.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为( )
A.8 B.6 C.4 D.2
【解答】解:如图,连接OC.
∵四边形OBCD是矩形,
∴∠OBC=90°,BD=OC=OA=10,
∴OB===6,
∴AB=OA﹣OB=4,
故选:C.
2.一个压路机的前轮直径是1.7米,如果前轮每分钟转动6周,那么这台压路机10分钟前进( )米.
A.51π B.102π C.153π D.204π
【解答】解:前轮的底面圆周长:π×1.7=1.7π(米),1.7π×6×10=102π(米)
故选:B.
3.如图,⊙O的弦AB垂直平分半径OC,若弦AB=2,则⊙O的半径为( )
A. B. C. D.2
【解答】解:连接OA,设OA=OC=r.
∵弦AB垂直平分半径OC,
∴OE=OC=r,AE=BE=,
在Rt△AOE中,由勾股定理得:r2=(r)2+()2,
解得r=2或﹣2(舍弃).
故选:D.
4.如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),下列不符合条件的OP的值是( )
A.4 B.3 C.3.5 D.2.5
【解答】解:连接OB,作OM⊥AB于M.
∵OM⊥AB,
∴AM=BM=AB=4,
在直角△OBM中,∵OB=5,BM=4,
∴OM===3.
∴3≤OP<5,
故选:D.
5.计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
若圆半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.d(25%)=1
B.当x>50%时,d(x)>1
C.当x1>x2时,d(x1)>d(x2)
D.当x1+x2=100%时,d(x1)=d(x2)
【解答】解:A、d(25%)=>1,本选项不符合题意.
B、当x>50%时,0≤d(x)<2,本选项不符合题意.
C、当x1>x2时,d(x1)与d(x2)可能相等,可能不等,本选项不符合题意.
D、当x1+x2=100%时,d(x1)=d(x2),本选项符合题意.
故选:D.
6.如图,已知四边形ABCD内接于⊙O,∠A=100°,则∠BOD=( )
A.80° B.50° C.160° D.100°
【解答】解:∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°,
∵∠A=100°,
∴∠C=180°﹣∠A=180°﹣100°=80°,
由圆周角定理得:∠BOD=2∠C=160°,
故选:C.
7.如图,AB是半圆O的直径,点C,D在半圆O上.若∠ABC=50°,则∠BDC的度数为( )
A.90° B.100° C.130° D.140°
【解答】解:∵AB是半圆O的直径,
∴∠ACB=90°.
又∠ABC=50°,
∴∠A=40°,
∵四边形ABDC为圆O的内接四边形,
∴∠A+∠BDC=180°,
∴∠BDC=140°,
故选:D.
8.如图,A,B,C是⊙O上的三个点,若∠B=32°,则∠AOC=( )
A.64° B.58° C.68° D.55°
【解答】解:如图,∵∠B=32°,
∴∠AOC=2∠B=2×32°=64°.
故选:A.
9.下列说法中一定正确的是( )
A.相等的圆心角所对的弧相等
B.圆上任意两点间的部分叫做圆弧
C.平分弦的直径垂直于弦
D.圆周角等于圆心角的一半
【解答】解:同圆或等圆中,相等的圆心角所对的弧相等,故A说法错误;
圆上任意两点间的部分叫做圆弧,故B说法正确;
平分弦(不是直径)的直径垂直于弦,故C说法错误;
同圆或等圆中,同弧所对的圆周角等于圆心角的一半,故D说法错误.
故选:B.
10.如图,已知BD是⊙O的直径,BD⊥AC于点E,∠AOC=100°,则∠BDC的度数是( )
A.20° B.25° C.30° D.40°
【解答】解:∵BD⊥AC,∠AOC=100°,
∴∠BOC=∠AOC=50°,
则∠BDC=∠BOC=25°,
故选:B.
二.填空题(共10小题)
11.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D= 25 度.
【解答】解:连接OB,
∵BD=OA,OA=OB
所以△AOB和△BOD为等腰三角形,
设∠D=x度,则∠OBA=2x°,
因为OB=OA,
所以∠A=2x°,
在△AOB中,2x+2x+(105﹣x)=180,
解得x=25,
即∠D=25°.
12.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP长为整数时,P点有 4 个.
【解答】解:解法一:过O作OC⊥AB于C,则AC=BC,
设OC=x,AC=y,
∵AB是⊙O的一条弦,⊙O的半径为6,
∴AB≤12,
∵△OAB的面积为18,
∴,
则y=,
∴,
解得x=3或﹣3(舍),
∴OC=3>4,
∴4<OP≤6,
∵点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
解法二:设△AOB中OA边上的高为h,
则,即,
∴h=6,
∵OB=6,
∴OA⊥OB,即∠AOB=90°,
∴AB=6,图中OC=3,
同理得:点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
故答案为:4.
13.如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的半径为2cm,则此时M、N两点间的距离是 2 cm.
【解答】解:根据题意得:EF=BC,MN=EF,
把该正方形纸片卷成一个圆柱,使点A与点D重合,则线段BC形成一半径为2cm的圆,线段BC是圆的周长,
BC=EF=2π×2=4π,
∴的长=EF==,
∴n=120°,即∠MON=120°,
∵OM=ON,
∴∠M=30°,
过O作OG⊥MN于G,
∵OM=2,
∴OG=1,MG=,
∴MN=2MG=2,
故答案为:2.
14.如图,AB是⊙O的直径,弦CD⊥AB于点E,且AE=CD=6,则⊙O的半径为 .
【解答】解:∵CD⊥AB,
∴CE=DE=CD,
∵AE=CD=6,
∴CE=DE=3,
∵OD=OB=OA,OE=AE﹣OA,
在Rt△ODE中,由勾股定理可得:OD2=DE2+(AE﹣OA)2,
即:OD2=32+(6﹣OD)2,
解得:OD=,
∴⊙O的半径为:,
故答案为:.
15.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,连结OC,若OC=5,AE=2,则CD= 8 .
【解答】解:∵AB为圆O的直径,弦CD⊥AB,
∴CD=2CE,
∵OC=5,AE=2,
∴OA=5,
∴OE=OA﹣AE=5﹣2=3,
∴CE=.
∴CD=2CE=8.
故答案为:8.
16.如图,点A、B、C、D、E在⊙O上,弧AB度数为30°,则∠E+∠C= 165° .
【解答】解:连接EA,
∵弧AB度数为30°,
∴∠AEB=15°,
∵四边形ACDE为⊙O的内接四边形,
∴∠C+∠AED=180°,
∴∠C+∠BED=180°﹣15°=165°,
故答案为:165°.
17.如图,四边形ABCD内接于⊙O,∠A:∠B:∠C=7:4:2.则∠D= 100° .
【解答】解:设∠A=7x,则∠B=4x,∠C=2x,
∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,∠B+∠D=180°,
∴2x+7x=180°,解得x=20°,
∴∠D=180°﹣4x=180°﹣80°=100°.
故答案为100°.
18.如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于 .
【解答】解:如图,
连接OA、OC,OC交AB于点E,
∵点C是弧AB中点,AB=6,
∴OC⊥AB,且AE=BE=3,
∵∠ADC=30°,
∴∠AOC=2∠ADC=60°,
∴∠OAE=30°,
∴OE=AE tan30°=3×=,
故圆心O到弦AB的距离为.
故答案为:.
19.如图,在锐角△ABC中,以BC为直径的半圆O分别交AB、AC于D、E两点,且∠A=45°,则S△ADE:S四边形DBCE的值为 1 .
【解答】解:连接BE,如图所示:
∵BC是⊙O的直径,
∴∠BEC=90°,
∴∠AEB=180°﹣90°=90°,
在Rt△ABE中,∠A=45°,
∴cosA=cos45°==,
∵四边形DBCE内接于⊙O,
∴∠ADE=∠ACB,∠AED=∠ABC,
∴△ADE∽△ACB,
∴===,
S△ADE:S四边形DBCE的值为1,
故答案为:1.
20.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,若AB=2DE,∠E=14°,则弧AC的度数为 42 °.
【解答】解:如图,连接OC、OD,
∵AB=2DE,
∴OD=DE,
∴∠E=∠EOD=14°,
在△EDO中,∠ODC=∠E+∠EOD=28°,
∵OC=OD,
∴∠OCD=∠ODC=28°,
在△CEO中,∠AOC=∠E+∠OCD=14°+28°=42°,
∴弧AC的度数为42°.
故答案为:42°.
第1页(共1页)
同课章节目录
