2.2.1.2对数的运算
图片预览



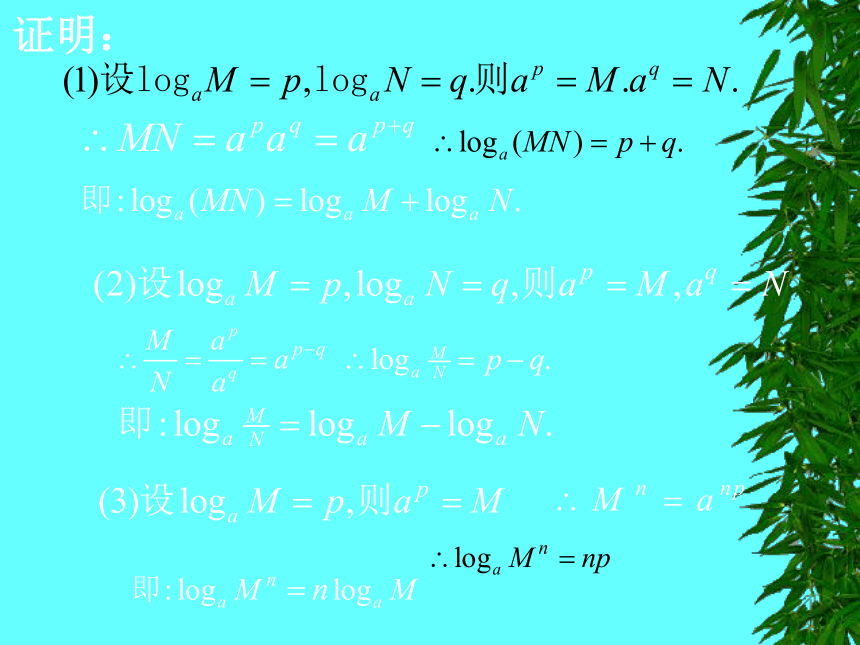



文档简介
(共17张PPT)
2.2.1.2对数的运算
湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作
复习上节内容
一般地,如果
那么数x叫做
记作:
以a为底N的对数(logarithm),
练习:
积、商、幂的对数运算法则:
如果 a > 0,a 1,M > 0, N > 0 有:
你能证明它们吗
我们可以运用转化的思想,先通过假设,将对数式化成指数式,并利用幂的运算性质进行恒等变形;然后再根据对数定义将指数式化成对数式。
证明:
几点说明
1、公式中为什么加上条件M>0,N>0?这是因为为了保证所得结果中的对数都存在,例如:lg[(-2)(-1)]=lg2存在,但lg(-2),lg(-1)都不存在。
2、公式要能够从左到右,从右到左熟练运用。
3、由性质1可得
由性质3可得常用的两个结论
4、注意把握运算性质的本质特征,避免犯下列错误。
三、知识应用
例4 计算
(1)
(2)
讲解范例
解 :
=5+14=19
解 :
例5 20世纪30年代,里克特制订了一种
表明地震能量大小的尺度,就是使用测
震仪衡量地震能量的等级,地震能量越
大,测震仪记录的地震曲线的振幅就越
大.这就是我们常说的里氏震级M,其计
算公式为 M=lgA-lgA0.
例题与练习
其中,A是被测地震的最大振幅,
A0是“标准地震”的振幅
(使用标准地震振幅是为了修正测震仪距
实际震中的距离造成的偏差).
例题与练习
(1)假设在一次地震中,一个距离震中100
千米的测震仪记录的地震最大振幅是20,
此时标准地震的振幅是0.001,计算这次
地震的震级(精确到0.1);
(2)5级地震给人的震感已比较明显,计算
7.6级地震的最大振幅是5级地震的最大振
幅的多少倍(精确到1).
例5 计算公式为 M=lgA-lgA0.
例题与练习
例6生物机体内碳14的“半衰期”为
5730年,湖南长沙马王堆汉墓女尸
出土时碳14的残余量约占76.7%,
试推算马王堆古墓的年代.
解:
解:
①
由①,②解得
②
例5
补充例题
练习 教材P.68练习第1、2、3、4题
小结
1、对数的运算性质。注意只有积、商、乘方才有运算性质,和、差没有.
2、对数运算性质在求值、化简中的运用,只有通过多做练习,才能达到准确、熟练,灵活应用公式
思 考
2.2.1.2对数的运算
湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作
复习上节内容
一般地,如果
那么数x叫做
记作:
以a为底N的对数(logarithm),
练习:
积、商、幂的对数运算法则:
如果 a > 0,a 1,M > 0, N > 0 有:
你能证明它们吗
我们可以运用转化的思想,先通过假设,将对数式化成指数式,并利用幂的运算性质进行恒等变形;然后再根据对数定义将指数式化成对数式。
证明:
几点说明
1、公式中为什么加上条件M>0,N>0?这是因为为了保证所得结果中的对数都存在,例如:lg[(-2)(-1)]=lg2存在,但lg(-2),lg(-1)都不存在。
2、公式要能够从左到右,从右到左熟练运用。
3、由性质1可得
由性质3可得常用的两个结论
4、注意把握运算性质的本质特征,避免犯下列错误。
三、知识应用
例4 计算
(1)
(2)
讲解范例
解 :
=5+14=19
解 :
例5 20世纪30年代,里克特制订了一种
表明地震能量大小的尺度,就是使用测
震仪衡量地震能量的等级,地震能量越
大,测震仪记录的地震曲线的振幅就越
大.这就是我们常说的里氏震级M,其计
算公式为 M=lgA-lgA0.
例题与练习
其中,A是被测地震的最大振幅,
A0是“标准地震”的振幅
(使用标准地震振幅是为了修正测震仪距
实际震中的距离造成的偏差).
例题与练习
(1)假设在一次地震中,一个距离震中100
千米的测震仪记录的地震最大振幅是20,
此时标准地震的振幅是0.001,计算这次
地震的震级(精确到0.1);
(2)5级地震给人的震感已比较明显,计算
7.6级地震的最大振幅是5级地震的最大振
幅的多少倍(精确到1).
例5 计算公式为 M=lgA-lgA0.
例题与练习
例6生物机体内碳14的“半衰期”为
5730年,湖南长沙马王堆汉墓女尸
出土时碳14的残余量约占76.7%,
试推算马王堆古墓的年代.
解:
解:
①
由①,②解得
②
例5
补充例题
练习 教材P.68练习第1、2、3、4题
小结
1、对数的运算性质。注意只有积、商、乘方才有运算性质,和、差没有.
2、对数运算性质在求值、化简中的运用,只有通过多做练习,才能达到准确、熟练,灵活应用公式
思 考
