2021-2022学年人教版七年级数学 上册4.3.2 角的比较与运算 课件(43张)
文档属性
| 名称 | 2021-2022学年人教版七年级数学 上册4.3.2 角的比较与运算 课件(43张) |  | |
| 格式 | zip | ||
| 文件大小 | 610.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 12:08:41 | ||
图片预览








文档简介
(共43张PPT)
人教版数学 七年级上册
第四章 几何图形初步
4.3 角
4.3.2 角的比较与运算
有一天学生小明和小华各带了一把折扇(如图所示),下面是他们的一段对话:
小明:我的折扇张开大一些,所以我的折扇的角也大一些.
小华:我的折扇长一些,所以我的折扇的角也大一些.
小明的折扇
小华的折扇
导入新知
A
B
C
D
E
F
怎样比较∠ABC和∠DEF的大小
1. 会比较两个角的大小,会计算两个角的和、差.
2. 弄清角平分线的含义,会用数学式子表示角平分线.
学习目标
线段长短的比较
AB>CD
ABAB=CD
新知一 角的大小与比较
合作探究
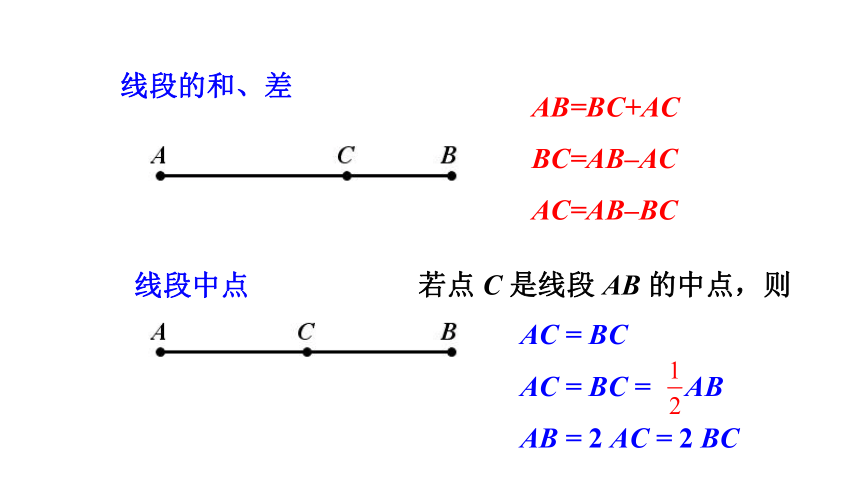
AB=BC+AC
BC=AB–AC
AC=AB–BC
线段的和、差
线段中点
若点 C 是线段 AB 的中点,则
AC = BC
AC = BC = AB
AB = 2 AC = 2 BC
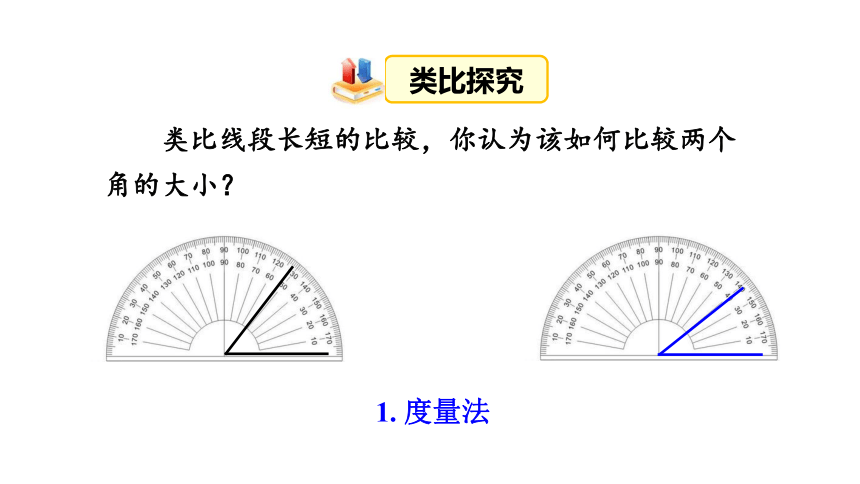
类比线段长短的比较,你认为该如何比较两个角的大小?
1. 度量法
类比探究
2. 叠合法
A
B
O
(O' )
B'
(A' )
A
B
O
A
B
O
(O' )
B'
(A' )
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
∠AOB>∠A'O'B'
(O' )
(B' )
(A' )
想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠A'O'B' )
图中有几个角?它们之间有什么关系?
图中有3个角:∠AOC,∠AOB,∠BOC.
∠AOC 是∠AOB 与∠BOC 的和,
记作∠AOC = ∠AOB +∠BOC;
它们的关系:
∠AOB 是∠AOC与∠BOC的差,记作∠AOB = ∠AOC–∠BOC;
类似地,∠AOC–∠AOB = .
∠BOC
A
B
O
C
例1 如图,O 是直线 AB 上一点,∠AOC=53°17′,
求∠BOC 的度数.
解:因为∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.
所以∠BOC=∠AOB–∠AOC
=180°– 53°17′
=179°60′–53°17′
=126°43′.
O
C
B
A
如何计算?
可以向 180 借
1 ,化为60′.
典例精析
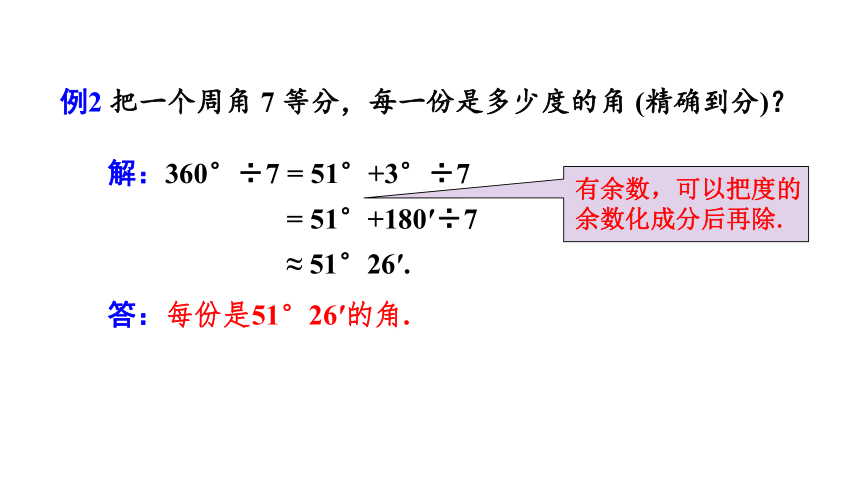
例2 把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7 = 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除.
B
A
O
C
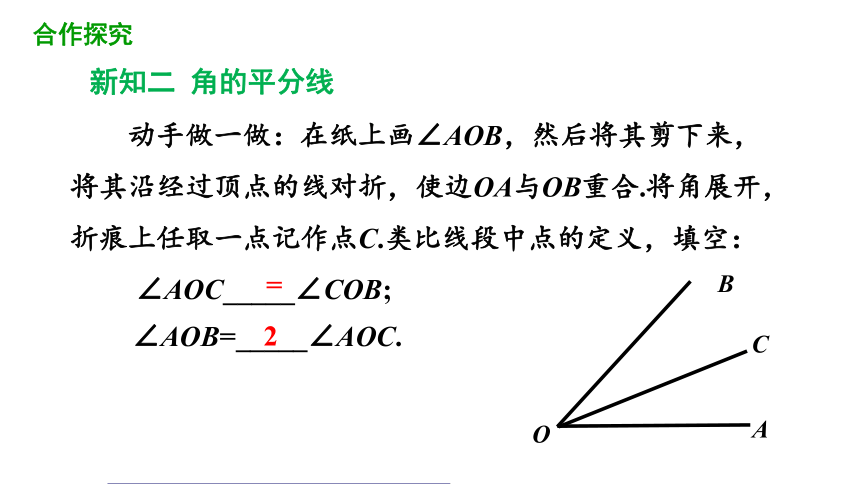
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
新知二 角的平分线
合作探究
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
O
B
A
C
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
因为 OC 是∠AOB 的角平分线,
所以 ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
例1 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
解: 因为 OB 平分∠AOC,∠AOC=80°,
O
A
B
C
D
E
所以 ∠BOC= ∠AOC
= ×80°=40°.
典例精析
(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
解:因为OB 平分∠AOC,
所以 ∠BOC=∠AOB = 40°.
因为OD 平分∠COE,
所以∠COD=∠DOE = 30°,
所以∠BOD =∠BOC+∠COD = 40°+30°= 70°.
O
A
B
C
D
E
(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB是多少度?
解:因为∠COD=30°,
OD 平分∠COE,
所以∠COE=2∠COD=60°,
所以∠AOC=∠AOE–∠COE=140°– 60°= 80°.
又因为OB 平分∠AOC,
O
A
B
C
D
E
所以∠AOB= ∠AOC= ×80°= 40°.
例2 如图,已知∠AOB=40°,自O点引射线OC,若∠AOC:∠COB=
2:3.求OC与∠AOB的平分线所成的角的度数.
O
A
B
解:分以下两种情况:
设∠AOC=2x,∠COB=3x,
因为∠AOB=40°,所以2x+3x=40°,得x=8°,
所以∠AOC=2x=2×8°=16°.
因为OD平分∠AOB,所以∠AOD=20°,
所以∠COD=∠AOD–∠AOC=20°–16°=4°.
C
D
如图,OC在∠AOB内部,OD平分∠AOB,
所以设∠AOC=2x,∠COB=3x,
因为∠AOB=40°,
所以3x–2x=40°,得x=40°,
所以∠AOC=2x=2×40°=80°,
因为OD平分∠AOB,所以∠AOD=20°,
所以∠COD=∠AOC+∠AOD=80°+20°=100°.
O
A
B
C
D
如图,OC在∠AOB外部,OD平分∠AOB,
所以OC与∠AOB的平分线所成的角的度数为4°或100°.
涉及到角度的计算时,除常规的和差倍分计算外,通常还需运用方程思想和分类讨论思想解决问题.
新知小结
1.已知∠MON=40°,∠NOP=15°,则∠MOP等于( )
A.55° B.25° C.55°或25° D.50°
2.一副三角板按如图方式摆放,且∠1比∠2大40°,则∠2的度数是( )
A.25° B.40° C.50° D.65°
C
A
课堂练习
3.如图,∠AOB=170°,∠AOC =∠BOD=90°,求∠COD的度数.
解:因为∠BOC =∠AOB– ∠AOC=170°–90°=80°,
所以∠COD=∠BOD–∠BOC=90°–80°=10°.
B
A
O
D
C
4.计算:86°23′12″–67°36′50″=_________.
解析: 86°23′12″–67°36′50″
= 86°22′72″–67°36′50″
= 85°82′72″–67°36′50″
= (85–67)°(82–36)′(72–50)″
=18°46′22″.
18°46′22″
5. 计算:(1)15°24′×5;
(2)31°42′÷5.
解:(1)15°24′×5=75°120′=77°;
(2)31°42′÷5=6°+1°42′÷5
=6°+102′÷5
=6°+20′+2′÷5
=6°20′+120″÷5
=6°20′+24″=6°20′24″.
角的大小比较
度量、叠合、翻折
角的和差
角的平分线
图形语言、文字语言、符号语言
方 法
作 法
描 述
归纳新知
1.在∠AOB的内部任取一点C,作射线OC,则一定存在( )
A.∠AOB>∠AOC
B.∠AOC=∠BOC
C.∠BOC>∠AOC
D.∠AOC>∠BOC
A
课后练习
2.如图所示的正方形网格中,∠ABC_____∠DEF.(填“>”“=”或“<”)
>
3.将一副三角板按如图所示的方式放置,则∠AOB=( )
A.30°
B.45°
C.75°
D.80°
C
4.下面等式成立的是( )
A.83.5°=83°50′
B.90°-57°23′27″=32°37′33″
C.15°48′36″+37°27′59″=52°16′35″
D.36°24′×4=145°36′
D
5.如图,∠AOC=∠BOD=80°,如果∠AOD=138°,那么∠BOC等于( )
A.22° B.32°
C.42° D.52°
A
D
7.如图,O是直线AB上一点,∠AOC=46°,OD是∠COB的平分线,则∠DOB等于( )
A.46° B.60°
C.67° D.76°
C
8.如图,OB是∠AOC的平分线,OC是∠AOD的平分线,
若∠COD=76°,那么∠AOD=_______,∠BOC=_______.
152°
38°
9.如图,BD平分∠ABC,BE把∠ABC分成2∶5的两部分,∠DBE=21°,求∠ABC的度数.
解:设∠ABE=2x°,则∠EBC=5x°.根据题意,
得2x+21=5x-21,解得x=14,所以∠ABC=14°×7=98°.
所以∠ABC的度数是98°.
10.如图,若∠AOC=∠BOD,则∠AOD与∠BOC的关系是( )
A.∠AOD>∠BOC B.∠AOD<∠BOC
C.∠AOD=∠BOC D.无法确定
C
11.如图所示的是一副特制的三角板,用它们可以画出一些特殊角.在下列选项中,不能用这副三角板画出的角度是( )
A.18° B.108°
C.82° D.117°
C
12.把一个平角7等分,每一份的度数是__________.(精确到分)
13.已知∠AOB=72°,若从点O引一条射线OC,使∠BOC=36°,则∠AOC的度数为________________.
25°43′
36°或108°
14.将一张长方形纸片按如图所示的方式折叠,BD,BE为折痕,并使BA′,BC′在同一条直线上.若∠ABE=15°,则∠DBC为____度.
75
15.如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
(1)若∠AOB=120°,则∠COE是多少度?
(2)如果∠BOC=3∠AOD,∠EOD-∠COD=30°,那么∠BOE是多少度?
16.已知直角三角板ABC和直角三角板DEF,∠ACB=∠EDF=90°,∠ABC=60°,∠DEF=45°.
(1)如图1,将顶点C和顶点D重合,保持三角板ABC不动,将三角板DEF绕点C旋转.当CF平分∠ACB时,求∠ACE的度数;
(2)在(1)的条件下,继续旋转三角板DEF,猜想∠ACE与∠BCF有怎样的数量关系?并利用图2所给的情形说明理由;
(3)如图3,将顶点C和顶点E重合,保持三角板ABC不动,将三角板DEF绕点C旋转.当CA落在∠DCF内部时,直接写出∠ACD与∠BCF之间的数量关系.
再 见
人教版数学 七年级上册
第四章 几何图形初步
4.3 角
4.3.2 角的比较与运算
有一天学生小明和小华各带了一把折扇(如图所示),下面是他们的一段对话:
小明:我的折扇张开大一些,所以我的折扇的角也大一些.
小华:我的折扇长一些,所以我的折扇的角也大一些.
小明的折扇
小华的折扇
导入新知
A
B
C
D
E
F
怎样比较∠ABC和∠DEF的大小
1. 会比较两个角的大小,会计算两个角的和、差.
2. 弄清角平分线的含义,会用数学式子表示角平分线.
学习目标
线段长短的比较
AB>CD
AB
新知一 角的大小与比较
合作探究
AB=BC+AC
BC=AB–AC
AC=AB–BC
线段的和、差
线段中点
若点 C 是线段 AB 的中点,则
AC = BC
AC = BC = AB
AB = 2 AC = 2 BC
类比线段长短的比较,你认为该如何比较两个角的大小?
1. 度量法
类比探究
2. 叠合法
A
B
O
(O' )
B'
(A' )
A
B
O
A
B
O
(O' )
B'
(A' )
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
∠AOB>∠A'O'B'
(O' )
(B' )
(A' )
想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠A'O'B' )
图中有几个角?它们之间有什么关系?
图中有3个角:∠AOC,∠AOB,∠BOC.
∠AOC 是∠AOB 与∠BOC 的和,
记作∠AOC = ∠AOB +∠BOC;
它们的关系:
∠AOB 是∠AOC与∠BOC的差,记作∠AOB = ∠AOC–∠BOC;
类似地,∠AOC–∠AOB = .
∠BOC
A
B
O
C
例1 如图,O 是直线 AB 上一点,∠AOC=53°17′,
求∠BOC 的度数.
解:因为∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.
所以∠BOC=∠AOB–∠AOC
=180°– 53°17′
=179°60′–53°17′
=126°43′.
O
C
B
A
如何计算?
可以向 180 借
1 ,化为60′.
典例精析
例2 把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7 = 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除.
B
A
O
C
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
新知二 角的平分线
合作探究
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
O
B
A
C
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
因为 OC 是∠AOB 的角平分线,
所以 ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
例1 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
解: 因为 OB 平分∠AOC,∠AOC=80°,
O
A
B
C
D
E
所以 ∠BOC= ∠AOC
= ×80°=40°.
典例精析
(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
解:因为OB 平分∠AOC,
所以 ∠BOC=∠AOB = 40°.
因为OD 平分∠COE,
所以∠COD=∠DOE = 30°,
所以∠BOD =∠BOC+∠COD = 40°+30°= 70°.
O
A
B
C
D
E
(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB是多少度?
解:因为∠COD=30°,
OD 平分∠COE,
所以∠COE=2∠COD=60°,
所以∠AOC=∠AOE–∠COE=140°– 60°= 80°.
又因为OB 平分∠AOC,
O
A
B
C
D
E
所以∠AOB= ∠AOC= ×80°= 40°.
例2 如图,已知∠AOB=40°,自O点引射线OC,若∠AOC:∠COB=
2:3.求OC与∠AOB的平分线所成的角的度数.
O
A
B
解:分以下两种情况:
设∠AOC=2x,∠COB=3x,
因为∠AOB=40°,所以2x+3x=40°,得x=8°,
所以∠AOC=2x=2×8°=16°.
因为OD平分∠AOB,所以∠AOD=20°,
所以∠COD=∠AOD–∠AOC=20°–16°=4°.
C
D
如图,OC在∠AOB内部,OD平分∠AOB,
所以设∠AOC=2x,∠COB=3x,
因为∠AOB=40°,
所以3x–2x=40°,得x=40°,
所以∠AOC=2x=2×40°=80°,
因为OD平分∠AOB,所以∠AOD=20°,
所以∠COD=∠AOC+∠AOD=80°+20°=100°.
O
A
B
C
D
如图,OC在∠AOB外部,OD平分∠AOB,
所以OC与∠AOB的平分线所成的角的度数为4°或100°.
涉及到角度的计算时,除常规的和差倍分计算外,通常还需运用方程思想和分类讨论思想解决问题.
新知小结
1.已知∠MON=40°,∠NOP=15°,则∠MOP等于( )
A.55° B.25° C.55°或25° D.50°
2.一副三角板按如图方式摆放,且∠1比∠2大40°,则∠2的度数是( )
A.25° B.40° C.50° D.65°
C
A
课堂练习
3.如图,∠AOB=170°,∠AOC =∠BOD=90°,求∠COD的度数.
解:因为∠BOC =∠AOB– ∠AOC=170°–90°=80°,
所以∠COD=∠BOD–∠BOC=90°–80°=10°.
B
A
O
D
C
4.计算:86°23′12″–67°36′50″=_________.
解析: 86°23′12″–67°36′50″
= 86°22′72″–67°36′50″
= 85°82′72″–67°36′50″
= (85–67)°(82–36)′(72–50)″
=18°46′22″.
18°46′22″
5. 计算:(1)15°24′×5;
(2)31°42′÷5.
解:(1)15°24′×5=75°120′=77°;
(2)31°42′÷5=6°+1°42′÷5
=6°+102′÷5
=6°+20′+2′÷5
=6°20′+120″÷5
=6°20′+24″=6°20′24″.
角的大小比较
度量、叠合、翻折
角的和差
角的平分线
图形语言、文字语言、符号语言
方 法
作 法
描 述
归纳新知
1.在∠AOB的内部任取一点C,作射线OC,则一定存在( )
A.∠AOB>∠AOC
B.∠AOC=∠BOC
C.∠BOC>∠AOC
D.∠AOC>∠BOC
A
课后练习
2.如图所示的正方形网格中,∠ABC_____∠DEF.(填“>”“=”或“<”)
>
3.将一副三角板按如图所示的方式放置,则∠AOB=( )
A.30°
B.45°
C.75°
D.80°
C
4.下面等式成立的是( )
A.83.5°=83°50′
B.90°-57°23′27″=32°37′33″
C.15°48′36″+37°27′59″=52°16′35″
D.36°24′×4=145°36′
D
5.如图,∠AOC=∠BOD=80°,如果∠AOD=138°,那么∠BOC等于( )
A.22° B.32°
C.42° D.52°
A
D
7.如图,O是直线AB上一点,∠AOC=46°,OD是∠COB的平分线,则∠DOB等于( )
A.46° B.60°
C.67° D.76°
C
8.如图,OB是∠AOC的平分线,OC是∠AOD的平分线,
若∠COD=76°,那么∠AOD=_______,∠BOC=_______.
152°
38°
9.如图,BD平分∠ABC,BE把∠ABC分成2∶5的两部分,∠DBE=21°,求∠ABC的度数.
解:设∠ABE=2x°,则∠EBC=5x°.根据题意,
得2x+21=5x-21,解得x=14,所以∠ABC=14°×7=98°.
所以∠ABC的度数是98°.
10.如图,若∠AOC=∠BOD,则∠AOD与∠BOC的关系是( )
A.∠AOD>∠BOC B.∠AOD<∠BOC
C.∠AOD=∠BOC D.无法确定
C
11.如图所示的是一副特制的三角板,用它们可以画出一些特殊角.在下列选项中,不能用这副三角板画出的角度是( )
A.18° B.108°
C.82° D.117°
C
12.把一个平角7等分,每一份的度数是__________.(精确到分)
13.已知∠AOB=72°,若从点O引一条射线OC,使∠BOC=36°,则∠AOC的度数为________________.
25°43′
36°或108°
14.将一张长方形纸片按如图所示的方式折叠,BD,BE为折痕,并使BA′,BC′在同一条直线上.若∠ABE=15°,则∠DBC为____度.
75
15.如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
(1)若∠AOB=120°,则∠COE是多少度?
(2)如果∠BOC=3∠AOD,∠EOD-∠COD=30°,那么∠BOE是多少度?
16.已知直角三角板ABC和直角三角板DEF,∠ACB=∠EDF=90°,∠ABC=60°,∠DEF=45°.
(1)如图1,将顶点C和顶点D重合,保持三角板ABC不动,将三角板DEF绕点C旋转.当CF平分∠ACB时,求∠ACE的度数;
(2)在(1)的条件下,继续旋转三角板DEF,猜想∠ACE与∠BCF有怎样的数量关系?并利用图2所给的情形说明理由;
(3)如图3,将顶点C和顶点E重合,保持三角板ABC不动,将三角板DEF绕点C旋转.当CA落在∠DCF内部时,直接写出∠ACD与∠BCF之间的数量关系.
再 见
