苏科版九年级数学上册 第1章一元二次方程小结与思考课件(共24张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 第1章一元二次方程小结与思考课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 483.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
小结与思考
一元二次方程小结与思考
初中数学
在一块长是32米、宽是24米的矩形空地内,要设计花圃,使花圃面积是矩形面积的一半。你能给出设计方案吗?
【问题情境】
例如:在空地中间开辟一个矩形的花圃,四周修筑同样宽的道路,道路的面积与花圃的面积相等。
32
24
x
x
x
x
你能计算出道路的宽吗?
一元二次方程的定义
只含有一个未知数,并且未知数的最高次数是2。像这样的方程叫做一元二次方程。
三个条件:
①只含一个未知数;
②未知数的最高次数是2;
③都是整式;
【针对训练】
1、判断下列关于x、y的方程一定是一元二次方程的有哪些?
√
×
×
×
×
×
√
在一块长是32米、宽是24米的矩形空地内,要设计花圃,使花圃面积是矩形面积的一半。你能给出设计方案吗?
【示范引领】
32
24
x
x
x
x
一元二次方程的一般形式
一般地,任何一个关于x的一元二次方程都可以化为 的形式,我们把
(a,b,c为常数,a≠0)称为一元二次方程的一般形式。
a x 2 + b x + c = 0
(a,b,c为常数,a≠0)
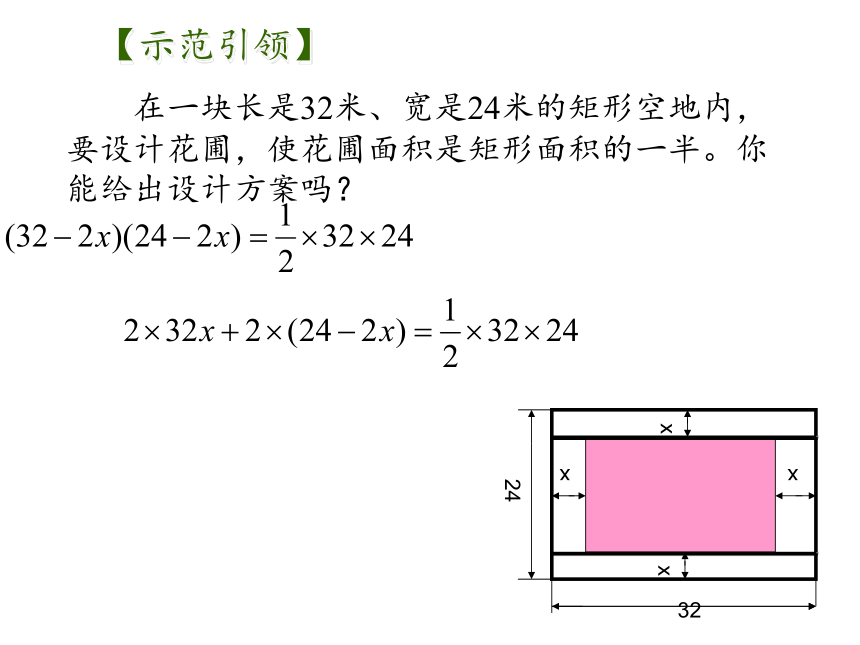
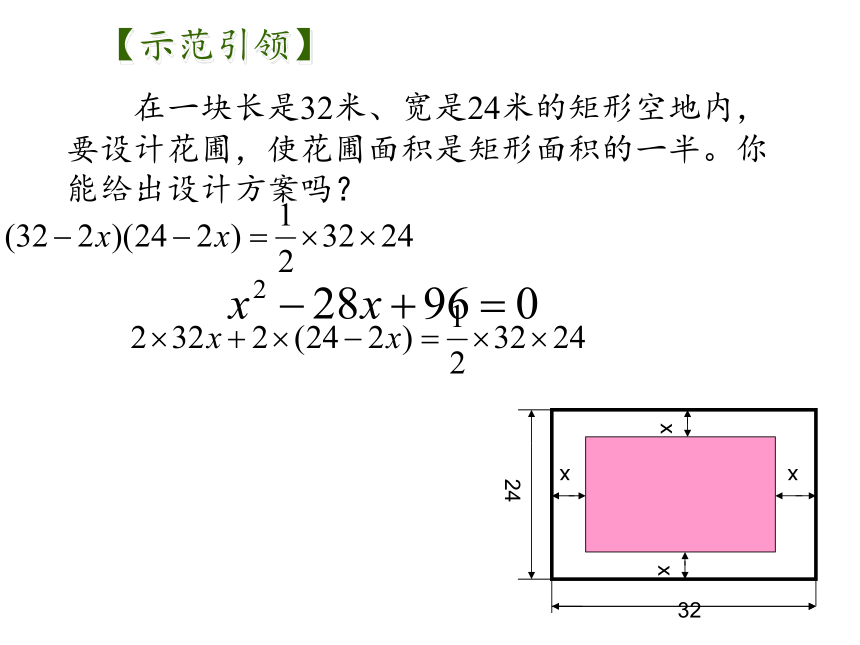
在一块长是32米、宽是24米的矩形空地内,要设计花圃,使花圃面积是矩形面积的一半。你能给出设计方案吗?
【示范引领】
32
24
x
x
x
x
公式法的产生
一元二次方程根的判别式
有两个不相等的实数根
有两个相等的实数根
无实数根(无解)
一元二次方程
判别式的情况
根的情况
公式法的应用
一元二次方程根与系数的关系
公式法的应用
【针对训练】
2、已知关于x的方程x2-3x+m = 0,
(1)若方程有两个不等实数根,则m的取值范围_____
(2)若方程的一个根是1 ,
则另一个根是_____,m的值是_______
解方程
基本思路:一元二次转化为一元一次
【求解】
转化的实质:降次
一元二次方程
一元一次方程
用“转化”的数学思想,尝试解方程
【能力提升】
在一块长是32米、宽是24米的矩形空地内,要设计花圃,使花圃面积是矩形面积的一半。你能给出设计方案吗?
【示范引领】
解:在空地中间开辟一个矩形的花圃,四周修筑同样宽的道路,使道路的面积与花圃的面积相等。
32
24
x
x
x
x
设道路的宽为x米,根据题意,得
答:当道路的宽为4米时,花圃面积是
矩形面积的一半。
(舍去)
定义
解法
应用
2个条件
利用检验过的一元二次方程的解去得出实际问题的答案
直接开平方法
配方法
公式法
因式分解法
数学源自生活
数学服务生活
(类比思想)
第一章 一元二次方程
一般形式
(转化思想)
根的判别式
根与系数的关系
知识框架
(数形结合)
32
20
【数学回归生活】
【数学回归生活】
探索:请你再设计两种不同的方案。
设计2:在矩形空地四个角设计四个完全相同的小正方形,连接其内侧的四个顶点,形成如图所示的5个小花圃。你能计算出小正方形的边长吗?
32
24
24-2x
32-2x
让生活走进数学
让数学回归生活
小结
通过本节课的复习你有了什么收获?
谢谢指导!
作业
必做题:
1.若等腰三角形底边长为8,腰长是方程x2-9x+20=0的一个根,求这个三角形的周长。
2.某厂今年1月的产值为50万元,第一季度共完成产值182万元,今年前两个月平均每月增长的百分率是多少
2、已知(1-m2-n2)(m2+n2)=-6,求m2+n2的值。
选做题:
作业
3、设m、n分别为x2+2x-2018=0的两个实数根,求m2+3m+n的值。
谢 谢
小结与思考
一元二次方程小结与思考
初中数学
在一块长是32米、宽是24米的矩形空地内,要设计花圃,使花圃面积是矩形面积的一半。你能给出设计方案吗?
【问题情境】
例如:在空地中间开辟一个矩形的花圃,四周修筑同样宽的道路,道路的面积与花圃的面积相等。
32
24
x
x
x
x
你能计算出道路的宽吗?
一元二次方程的定义
只含有一个未知数,并且未知数的最高次数是2。像这样的方程叫做一元二次方程。
三个条件:
①只含一个未知数;
②未知数的最高次数是2;
③都是整式;
【针对训练】
1、判断下列关于x、y的方程一定是一元二次方程的有哪些?
√
×
×
×
×
×
√
在一块长是32米、宽是24米的矩形空地内,要设计花圃,使花圃面积是矩形面积的一半。你能给出设计方案吗?
【示范引领】
32
24
x
x
x
x
一元二次方程的一般形式
一般地,任何一个关于x的一元二次方程都可以化为 的形式,我们把
(a,b,c为常数,a≠0)称为一元二次方程的一般形式。
a x 2 + b x + c = 0
(a,b,c为常数,a≠0)
在一块长是32米、宽是24米的矩形空地内,要设计花圃,使花圃面积是矩形面积的一半。你能给出设计方案吗?
【示范引领】
32
24
x
x
x
x
公式法的产生
一元二次方程根的判别式
有两个不相等的实数根
有两个相等的实数根
无实数根(无解)
一元二次方程
判别式的情况
根的情况
公式法的应用
一元二次方程根与系数的关系
公式法的应用
【针对训练】
2、已知关于x的方程x2-3x+m = 0,
(1)若方程有两个不等实数根,则m的取值范围_____
(2)若方程的一个根是1 ,
则另一个根是_____,m的值是_______
解方程
基本思路:一元二次转化为一元一次
【求解】
转化的实质:降次
一元二次方程
一元一次方程
用“转化”的数学思想,尝试解方程
【能力提升】
在一块长是32米、宽是24米的矩形空地内,要设计花圃,使花圃面积是矩形面积的一半。你能给出设计方案吗?
【示范引领】
解:在空地中间开辟一个矩形的花圃,四周修筑同样宽的道路,使道路的面积与花圃的面积相等。
32
24
x
x
x
x
设道路的宽为x米,根据题意,得
答:当道路的宽为4米时,花圃面积是
矩形面积的一半。
(舍去)
定义
解法
应用
2个条件
利用检验过的一元二次方程的解去得出实际问题的答案
直接开平方法
配方法
公式法
因式分解法
数学源自生活
数学服务生活
(类比思想)
第一章 一元二次方程
一般形式
(转化思想)
根的判别式
根与系数的关系
知识框架
(数形结合)
32
20
【数学回归生活】
【数学回归生活】
探索:请你再设计两种不同的方案。
设计2:在矩形空地四个角设计四个完全相同的小正方形,连接其内侧的四个顶点,形成如图所示的5个小花圃。你能计算出小正方形的边长吗?
32
24
24-2x
32-2x
让生活走进数学
让数学回归生活
小结
通过本节课的复习你有了什么收获?
谢谢指导!
作业
必做题:
1.若等腰三角形底边长为8,腰长是方程x2-9x+20=0的一个根,求这个三角形的周长。
2.某厂今年1月的产值为50万元,第一季度共完成产值182万元,今年前两个月平均每月增长的百分率是多少
2、已知(1-m2-n2)(m2+n2)=-6,求m2+n2的值。
选做题:
作业
3、设m、n分别为x2+2x-2018=0的两个实数根,求m2+3m+n的值。
谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
