专题11 抛物线 同步学案(含解析)
文档属性
| 名称 | 专题11 抛物线 同步学案(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 00:00:00 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
专题11抛物线
考点一 抛物线的定义
1.定义:平面内与一定点F和一条定直线l(不经过点F)距离相等的点的轨迹.
2.焦点:定点F.
3.准线:定直线l.
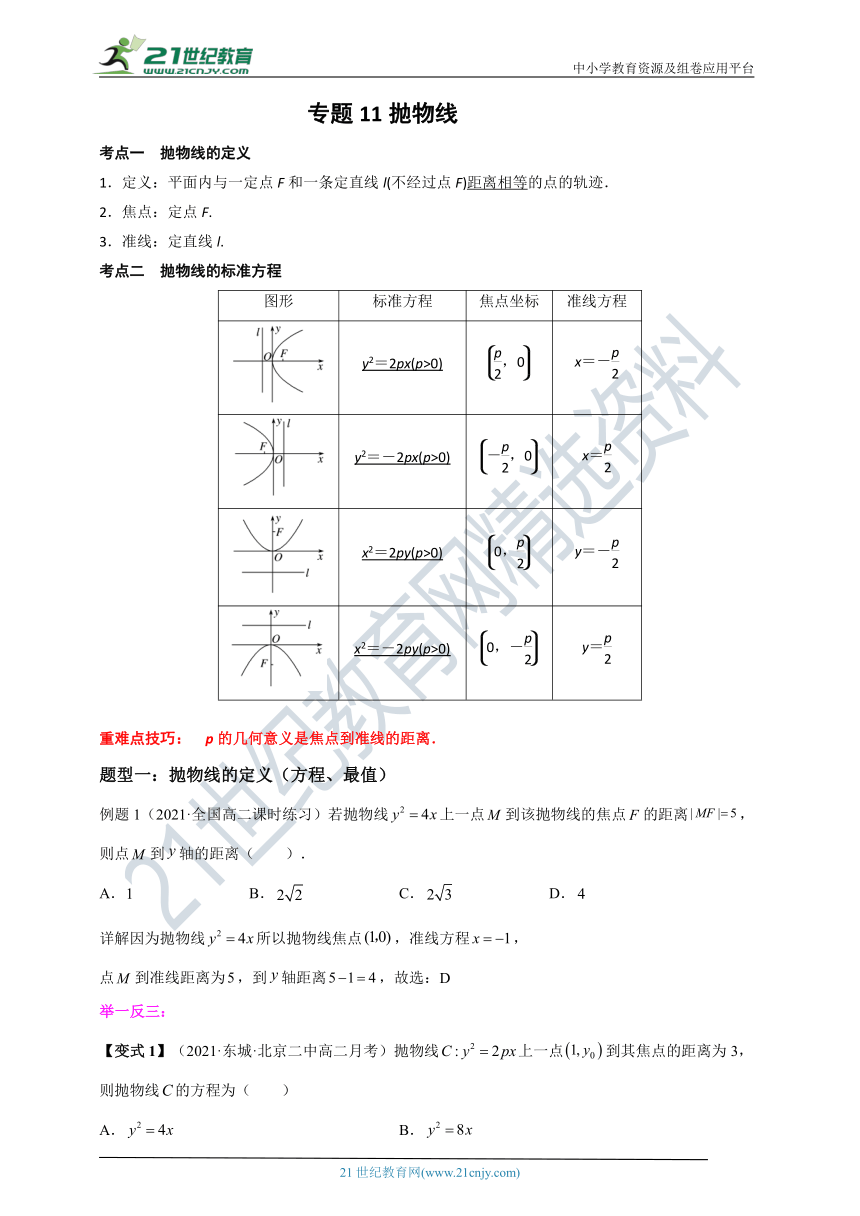
考点二 抛物线的标准方程
图形 标准方程 焦点坐标 准线方程
y2=2px(p>0) x=-
y2=-2px(p>0) x=
x2=2py(p>0) y=-
x2=-2py(p>0) y=
重难点技巧: p的几何意义是焦点到准线的距离.
题型一:抛物线的定义(方程、最值)
例题1(2021·全国高二课时练习)若抛物线上一点到该抛物线的焦点的距离,则点到轴的距离( ).
A. B. C. D.
详解因为抛物线所以抛物线焦点,准线方程,
点到准线距离为,到轴距离,故选:D
举一反三:
【变式1】(2021·东城·北京二中高二月考)抛物线上一点到其焦点的距离为3,则抛物线的方程为( )
A. B.
C. D.
【详解】因抛物线上一点到其焦点的距离为3,则p>0,抛物线准线方程为,
由抛物线定义得:,解得,所以抛物线的方程为:.故选:B
【变式2】(2021·全国高二课时练习)已知A(3,2),点F为抛物线的焦点,点P在抛物线上移动,为使取得最小值,则点P的坐标为( )
A.(0,0) B.(2,2) C. D.
【详解】
如图所示:
设点P到准线的距离为,准线方程为,
所以,当且仅当点为与抛物线的交点时,取得最小值,此时点P的坐标为.故选:B.
题型二:抛物线的四种标准方程
例题2(2021·全国高二课时练习)以轴为对称轴,顶点为坐标原点,焦点与原点之间的距离为2的抛物线方程是( )
A. B.
C.或 D.或
【详解】
依题意设抛物线方程为.因为焦点与原点之间的距离为2,所以,所以,所以抛物线方程为或.故选:C.
举一反三:
【变式1】(2021·吉林农安·高二期末(理))已知抛物线C:()的准线为l,圆M:与l相切,则( )
A.1 B.2 C.3 D.4
【详解】抛物线的准线与圆相切,
可得,解得.故选:B.
【变式2】(2021·四川省内江市第六中学(理))已知抛物线的焦点与椭圆的一个焦点重合,则( )
A. B. C. D.
【详解】抛物线的焦点坐标为,
所以椭圆中,,.故选:C.
题型三:抛物线焦半径的公式
例题3(2021·全国)已知抛物线的焦点为,,是抛物线上两个不同的点,若,则线段的中点到轴的距离为( )
A.3 B. C.5 D.
【详解】由抛物线方程,得其准线方程为.设,,由抛物线的定义,得,即,所以线段中点的横坐标为,线段的中点到轴的距离为.故选:B.
举一反三:
【变式1】(2021·全国高二课时练习)过抛物线的焦点的直线交于,两点,若,则( )
A.3 B.2 C. D.1
【详解】依题意,直线不与轴垂直,设直线的方程为,将其代入抛物线的方程,得.设,,则.因为,所以,即,,所以,解得.故选:C.
【变式2】(2021·全国高二课时练习)已知抛物线C:y2=4x的焦点为F,设A和B是C上的两点,且M是线段AB的中点,若|AB|=6,则M到y轴的距离的最小值是( )
A.2 B.4 C.6 D.8
解:因为C的方程为y2=4x,所以F(1,0),
过A作准线x=﹣1的垂线,垂足为E,过B作准线的垂线,垂足为D,过M作准线的垂线,垂足为K,
根据抛物线定义可得:|AF|+|BF|=|AE|+|BD|≥|AB|=6,
则|MK|=(|AE|+|BD|)≥3,
所以,线段MN的中点M到C的准线x=﹣1的距离最小值为3,
故点M到y轴的距离最小值为3﹣1=2.
故选:A.
题型四:抛物线的方程常见求法
例题4(2021·东城·北京二中高二月考)己知过点的抛物线方程为,过此抛物线的焦点的直线与抛物线交于,两点,且.
(1)求抛物线的方程、焦点坐标、准线方程;
(2)求所在的直线方程.
【详解】(1)因点在抛物线方程上,则,
所以抛物线的方程为,焦点,准线方程为:;
(2)显然,直线不垂直y轴,设直线方程为:,
由消去x得:,设,则有,
于是得,解得,即直线AB:,
所以所在的直线方程:或.
举一反三:
【变式1】(2021·哈密市第十五中学(理))根据条件求下列方程.
(1)顶点在原点,准线方程是的抛物线方程;
(2)已知双曲线过点并且与有共同的渐近线,求双曲线的标准方程.
【详解】(1)∵ 抛物线的顶点在原点,准线方程是,
∴ 可设抛物线的方程为,且p=4,
∴ 抛物线的标准方程为,
(2)∵双曲线与双曲线有共同的渐近线,
∴ 可设双曲线方程为,
又双曲线过点,∴ ,∴ ,
故双曲线的标准方程.
【变式2】(2021·全国高二专题练习)根据下列条件求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)过点P(2,-4);
(3)抛物线的焦点在x轴上,直线y=-3与抛物线交于点A,|AF|=5.
【详解】(1)双曲线方程为,其左顶点为(-3,0),
由题意设抛物线方程为y2=-2px(p>0),则抛物线焦点为,,解得p=6,
所以所求抛物线方程为为y2=-12x;
(2)由于P(2,-4)在第四象限且抛物线的对称轴为坐标轴,可设方程为y2=mx或x2=ny,
将P点坐标代入方程求得m=8,n=-1,
所以所求抛物线方程为y2=8x或x2=-y;
(3)设所求焦点在x轴上的抛物线方程为:y2=2px(p≠0),A(m,-3),则抛物线准线为,
由抛物线定义得,又(-3)2=2pm,显然p,m同号,
从而得 或,解得p=±1或p=±9,
所以所求抛物线方程为y2=±2x或y2=±18x.
考点三 抛物线的简单几何性质
标准方程 y2=2px(p>0) y2=-2px(p>0) x2=2py(p>0) x2=-2py(p>0)
图形
范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
对称轴 x轴 x轴 y轴 y轴
焦点坐标 F F F F
准线方程 x=- x= y=- y=
顶点坐标 O(0,0)
离心率 e=1
通径长 2p
考点四 直线与抛物线的位置关系
直线y=kx+b与抛物线y2=2px(p>0)的交点个数决定于关于x的方程组解的个数,即二次方程k2x2+2(kb-p)x+b2=0解的个数.当k≠0时,若Δ>0,则直线与抛物线有两个不同的公共点;若Δ=0,直线与抛物线有一个公共点;若Δ<0,直线与抛物线没有公共点.当k=0时,直线与抛物线的轴平行或重合,此时直线与抛物线有1个公共点.
考点五 直线和抛物线
1.抛物线的通径(过焦点且垂直于轴的弦)长为2p.
2.抛物线的焦点弦
过抛物线y2=2px(p>0)的焦点F的一条直线与它交于两点A(x1,y1),B(x2,y2),则
①y1y2=-p2,x1x2=;②=x1+x2+p;③+=.
题型五:抛物线的简单性质(顶点、焦点)
例题5(2020·全国高二)对抛物线,下列描述正确的是( )
A.开口向上,焦点为 B.开口向上,焦点为
C.开口向右,焦点为 D.开口向右,焦点为
【详解】由题知,该抛物线的标准方程为,
则该抛物线开口向上,焦点坐标为.故选:A.
举一反三:
【变式1】(2021·全国高二(文))点到抛物线的准线的距离为6,那么抛物线的标准方程是( )
A. B.或
C. D.或
【详解】将转化为,
当时,抛物线开口向上,准线方程,点到准线的距离为,解得,所以抛物线方程为,即;
当时,抛物线开口向下,准线方程,点到准线的距离为,解得或(舍去),所以抛物线方程为,即.
所以抛物线的方程为或故选:D
【变式2】(2017·河南信阳·高二期末(理))抛物线的焦点坐标为
A. B. C. D.
【详解】将化为,则抛物线的焦点坐标为.故选B.
题型六:抛物线的对称性
例题6(2021·全国高二单元测试)以抛物线的顶点为圆心的圆交于,两点,交的准线于,两点,已知,,则抛物线的焦点到准线的距离为( )
A.2 B.4 C.6 D.8
解:不妨设抛物线的方程为,令点在第一象限,点在第二象限.
根据抛物线的对称性,得点的纵坐标为,代入抛物线的方程得,即点.
又点.因为点,都在以坐标原点为圆心的圆上,所以,解得或(舍去),
则抛物线的焦点到准线的距离为4.故选:B.
举一反三:
【变式1】(2021·中国农业大学附属中学)若正三角形的顶点都在抛物线上,其中一个顶点恰为坐标原点,则这个三角形的面积是( )
A. B. C. D.
【详解】设三角形其中一个顶点为,
因为三角形是正三角形,
所以,即,解得,
所以三角形的两个顶点为,
所以三角形的面积为,故选:A
【变式2】(2021·全国高二课时练习)是抛物线上的两点,为坐标原点.若,且的面积为,则( )
A. B. C. D.
【详解】如图,
∵,知两点关于轴对称,
设,
∴,解得,
∴,∴,
∴,∴.故选:C
题型七:抛物线的弦长问题
例题7.(2021·全国高二课时练习)过抛物线的焦点作直线交抛物线于,两点(,的横坐标不相等),弦的垂直平分线交轴于点,若,则( )
A.14 B.16 C.18 D.20
设,,弦的中点为,,
则,
所以,所以,
则,
所以弦的垂直平分线为.
令,则,所以.
又,
所以.故选:D.
举一反三:
【变式1】(2021·马鞍山市第二中学郑蒲港分校高二开学考试(文))过拋物线:焦点F的直线与抛物线相交于A,B两点,,O为坐标原点,且△的面积为,则抛物线C的标准方程为( )
A. B. C. D.
【详解】由题设,令为,联立抛物线方程并整理得,
∴若,则,,又易得,
∴,则,即,
∴,
又,而,
∴,即,又,则,故.故选:D
【变式2】(2021·河北运河·沧州市一中高二开学考试)已知直线与抛物线:相交于,两点,为抛物线的焦点.若,则等于( )
A.7 B.8 C.9 D.10
【详解】,又,
,
,
直线方程为,代入抛物线方程,得:
,
,
,故选:C.
题型八:抛物线的焦点弦性质问题
例题8(2021·全国高二课时练习)已知抛物线的顶点在原点,焦点在轴正半轴上,过其焦点作直线交抛物线于,两点,过点,分别作抛物线准线的垂线,垂足分别为点,,,且,则该抛物线的方程为( )
【详解】设,,,
抛物线的方程为,,
由可得,
所以
所以,,
所以,,,,
所以,, ,,
所以,
因为,所以,所以,
所以抛物线的方程为.故选:A.
举一反三:
【变式1】(2020·江苏高二课前预习)已知抛物线的顶点在坐标原点,准线方程为,过其焦点的直线与抛物线交于,两点,若直线的斜率为1,则弦的长为( )
A.4 B.6 C.7 D.8
解:依题意得,抛物线的方程是,直线的方程是.联立
消去,得,即.设,,则,所以.
故选:D.
【变式2】(2021·四川自贡·高二期末(文))已知抛物线的焦点为,准线为,过焦点的直线交抛物线于、两点,、两点分别为、两点在直线上的射影,而且,为线段的中点.则下列命题( )
① ②等腰直角三角形
③直线的斜率为
④的面积为4(为坐标原点),其中正确的命题个数为( )
A.1 B.2 C.3 D.4
【详解】根据题意可得焦点F(1,0),准线方程为x=-1,由题意可得直线BA的斜率不为0,
可设直线AB的方程为x=my+1设A(x1,y1),B(x2,y2),由题意可知,将直线AB与抛物线方程联立得y2-4my-4=0所以.
对于①:所以FC⊥FD,即∠CFD=90°,故①正确;
对于②:由①可得,不可能CM⊥DM,更不会∠C或∠D为直角,故B不正确;
对于③:因为,所以,即,
因为所以解得,所以,
所以直线的斜率为.故③正确;
对于④:由題意可得,
点O到直线AB的距离,
所以,故④错误.故选:B
题型九:直线与抛物线的位置关系
例题9(2021·贵州师大附中高二月考(理))已知抛物线:,过其焦点且斜率为2的直线与抛物线交于,两点,若线段中点的纵坐标为1,则抛物线的准线方程为( )
A. B. C. D.
【详解】抛物线的焦点坐标为,
所以直线AB为,将其代入抛物线方程可得,
设,则,因为线段中点的纵坐标为1,所以,所以准线方程为,故选:B
举一反三:
【变式1】(2021·全国高二课时练习)直线与抛物线有且只有一个公共点,则,满足的条件是( )
A. B.,
C., D.或
【详解】当时,直线与抛物线有且只有一个公共点,符合题意;
当时,由可得:,
若直线与抛物线有且只有一个公共点,
则,整理可得:,所以,
综上所述:或,故选:D.
【变式2】(2021·全国高二课时练习)已知点,在抛物线上,为坐标原点,若,且的垂心恰好是此抛物线的焦点,则直线的方程是( )
A. B. C. D.
【详解】如图所示,为的垂心,为焦点,
,垂直平分线段,直线垂直于轴.
设,,其中.
为垂心,,,
即,解得,
直线的方程为,即.
故选:C.
题型十:抛物线的定值、定点、定直线问题
例题10(2021·全国高二课时练习)已知抛物线的顶点在坐标原点,焦点在轴的正半轴上,直线与抛物线交于,两点,且.
(1)求抛物线的标准方程.
(2)在轴上是否存在一点,使为正三角形?若存在,求出点的坐标;若不存在,请说明理由.
【详解】(1)由题意,设所求抛物线的标准方程为.
由,消去,得.
设,,则,.
由,
得,解得或(舍去),
∴抛物线的标准方程为.
(2)设的中点为点,则.
假设在轴上存在满足条件的点,连接.
∵为正三角形,∴,即,
解得,∴,∴.
又,
∴在轴上不存在一点,使为正三角形.
举一反三:
【变式1】(2021·全国高二课时练习) 已知抛物线C:y2=4x,A,B,其中m>0,过B的直线l交抛物线C于M,N.
(1)当m=5,且直线l垂直于x轴时,求证:△AMN为直角三角形;
(2)若=+,当点P在直线l上时,求实数m,使得AM⊥AN.
解:(1)证明:由题意,l:x=5,代入y2=4x中,解得,
不妨取M(5,),N(5,-),则,
∴,∴AM⊥AN,即△AMN为直角三角形,得证.
(2)由题意,四边形OAPB为平行四边形,则kBP=kOA=2,
设直线l:y=2(x-m),,联立,得y2-2y-4m=0,
由题意,判别式Δ=4+16m>0,y1+y2=2,y1y2=-4m,
∵AM⊥AN,则,又,
∴,化简得(y1+2)(y2+2)+16=0,即y1y2+2(y1+y2)+20=0,
∴,解得m=6,故m=6时,有AM⊥AN.
【变式2】(2021·重庆市第六十六中学校高二月考)已知动圆过定点,且与直线相切,
(1)求动圆圆心的轨迹方程;
(2)过点作曲线的两条弦,设、所在直线的斜率分别为、,当、变化且满足时,证明直线恒过定点,并求出该定点的坐标.
解:(1)∵动圆过定点,且与直线相切,
∴曲线是以点为焦点,直线为准线的抛物线,其方程为:.
(2)∵直线与抛物线有两个不同的交点
∴直线的斜率必不为0.
∴设其方程为,并设点,点,与抛物线联立得:.
∴整理得:,其中,,且
∵
.
∴.
∴.
∴.
∴.
∴或.
当时,直线的方程可化为:,过定点;
当时,直线的方程可化为:,过定点,即点不合题意,舍去.
∴直线必过定点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题11抛物线
考点一 抛物线的定义
1.定义:平面内与一定点F和一条定直线l(不经过点F)距离相等的点的轨迹.
2.焦点:定点F.
3.准线:定直线l.
考点二 抛物线的标准方程
图形 标准方程 焦点坐标 准线方程
y2=2px(p>0) x=-
y2=-2px(p>0) x=
x2=2py(p>0) y=-
x2=-2py(p>0) y=
重难点技巧: p的几何意义是焦点到准线的距离.
题型一:抛物线的定义(方程、最值)
例题1(2021·全国高二课时练习)若抛物线上一点到该抛物线的焦点的距离,则点到轴的距离( ).
A. B. C. D.
详解因为抛物线所以抛物线焦点,准线方程,
点到准线距离为,到轴距离,故选:D
举一反三:
【变式1】(2021·东城·北京二中高二月考)抛物线上一点到其焦点的距离为3,则抛物线的方程为( )
A. B.
C. D.
【详解】因抛物线上一点到其焦点的距离为3,则p>0,抛物线准线方程为,
由抛物线定义得:,解得,所以抛物线的方程为:.故选:B
【变式2】(2021·全国高二课时练习)已知A(3,2),点F为抛物线的焦点,点P在抛物线上移动,为使取得最小值,则点P的坐标为( )
A.(0,0) B.(2,2) C. D.
【详解】
如图所示:
设点P到准线的距离为,准线方程为,
所以,当且仅当点为与抛物线的交点时,取得最小值,此时点P的坐标为.故选:B.
题型二:抛物线的四种标准方程
例题2(2021·全国高二课时练习)以轴为对称轴,顶点为坐标原点,焦点与原点之间的距离为2的抛物线方程是( )
A. B.
C.或 D.或
【详解】
依题意设抛物线方程为.因为焦点与原点之间的距离为2,所以,所以,所以抛物线方程为或.故选:C.
举一反三:
【变式1】(2021·吉林农安·高二期末(理))已知抛物线C:()的准线为l,圆M:与l相切,则( )
A.1 B.2 C.3 D.4
【详解】抛物线的准线与圆相切,
可得,解得.故选:B.
【变式2】(2021·四川省内江市第六中学(理))已知抛物线的焦点与椭圆的一个焦点重合,则( )
A. B. C. D.
【详解】抛物线的焦点坐标为,
所以椭圆中,,.故选:C.
题型三:抛物线焦半径的公式
例题3(2021·全国)已知抛物线的焦点为,,是抛物线上两个不同的点,若,则线段的中点到轴的距离为( )
A.3 B. C.5 D.
【详解】由抛物线方程,得其准线方程为.设,,由抛物线的定义,得,即,所以线段中点的横坐标为,线段的中点到轴的距离为.故选:B.
举一反三:
【变式1】(2021·全国高二课时练习)过抛物线的焦点的直线交于,两点,若,则( )
A.3 B.2 C. D.1
【详解】依题意,直线不与轴垂直,设直线的方程为,将其代入抛物线的方程,得.设,,则.因为,所以,即,,所以,解得.故选:C.
【变式2】(2021·全国高二课时练习)已知抛物线C:y2=4x的焦点为F,设A和B是C上的两点,且M是线段AB的中点,若|AB|=6,则M到y轴的距离的最小值是( )
A.2 B.4 C.6 D.8
解:因为C的方程为y2=4x,所以F(1,0),
过A作准线x=﹣1的垂线,垂足为E,过B作准线的垂线,垂足为D,过M作准线的垂线,垂足为K,
根据抛物线定义可得:|AF|+|BF|=|AE|+|BD|≥|AB|=6,
则|MK|=(|AE|+|BD|)≥3,
所以,线段MN的中点M到C的准线x=﹣1的距离最小值为3,
故点M到y轴的距离最小值为3﹣1=2.
故选:A.
题型四:抛物线的方程常见求法
例题4(2021·东城·北京二中高二月考)己知过点的抛物线方程为,过此抛物线的焦点的直线与抛物线交于,两点,且.
(1)求抛物线的方程、焦点坐标、准线方程;
(2)求所在的直线方程.
【详解】(1)因点在抛物线方程上,则,
所以抛物线的方程为,焦点,准线方程为:;
(2)显然,直线不垂直y轴,设直线方程为:,
由消去x得:,设,则有,
于是得,解得,即直线AB:,
所以所在的直线方程:或.
举一反三:
【变式1】(2021·哈密市第十五中学(理))根据条件求下列方程.
(1)顶点在原点,准线方程是的抛物线方程;
(2)已知双曲线过点并且与有共同的渐近线,求双曲线的标准方程.
【详解】(1)∵ 抛物线的顶点在原点,准线方程是,
∴ 可设抛物线的方程为,且p=4,
∴ 抛物线的标准方程为,
(2)∵双曲线与双曲线有共同的渐近线,
∴ 可设双曲线方程为,
又双曲线过点,∴ ,∴ ,
故双曲线的标准方程.
【变式2】(2021·全国高二专题练习)根据下列条件求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)过点P(2,-4);
(3)抛物线的焦点在x轴上,直线y=-3与抛物线交于点A,|AF|=5.
【详解】(1)双曲线方程为,其左顶点为(-3,0),
由题意设抛物线方程为y2=-2px(p>0),则抛物线焦点为,,解得p=6,
所以所求抛物线方程为为y2=-12x;
(2)由于P(2,-4)在第四象限且抛物线的对称轴为坐标轴,可设方程为y2=mx或x2=ny,
将P点坐标代入方程求得m=8,n=-1,
所以所求抛物线方程为y2=8x或x2=-y;
(3)设所求焦点在x轴上的抛物线方程为:y2=2px(p≠0),A(m,-3),则抛物线准线为,
由抛物线定义得,又(-3)2=2pm,显然p,m同号,
从而得 或,解得p=±1或p=±9,
所以所求抛物线方程为y2=±2x或y2=±18x.
考点三 抛物线的简单几何性质
标准方程 y2=2px(p>0) y2=-2px(p>0) x2=2py(p>0) x2=-2py(p>0)
图形
范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
对称轴 x轴 x轴 y轴 y轴
焦点坐标 F F F F
准线方程 x=- x= y=- y=
顶点坐标 O(0,0)
离心率 e=1
通径长 2p
考点四 直线与抛物线的位置关系
直线y=kx+b与抛物线y2=2px(p>0)的交点个数决定于关于x的方程组解的个数,即二次方程k2x2+2(kb-p)x+b2=0解的个数.当k≠0时,若Δ>0,则直线与抛物线有两个不同的公共点;若Δ=0,直线与抛物线有一个公共点;若Δ<0,直线与抛物线没有公共点.当k=0时,直线与抛物线的轴平行或重合,此时直线与抛物线有1个公共点.
考点五 直线和抛物线
1.抛物线的通径(过焦点且垂直于轴的弦)长为2p.
2.抛物线的焦点弦
过抛物线y2=2px(p>0)的焦点F的一条直线与它交于两点A(x1,y1),B(x2,y2),则
①y1y2=-p2,x1x2=;②=x1+x2+p;③+=.
题型五:抛物线的简单性质(顶点、焦点)
例题5(2020·全国高二)对抛物线,下列描述正确的是( )
A.开口向上,焦点为 B.开口向上,焦点为
C.开口向右,焦点为 D.开口向右,焦点为
【详解】由题知,该抛物线的标准方程为,
则该抛物线开口向上,焦点坐标为.故选:A.
举一反三:
【变式1】(2021·全国高二(文))点到抛物线的准线的距离为6,那么抛物线的标准方程是( )
A. B.或
C. D.或
【详解】将转化为,
当时,抛物线开口向上,准线方程,点到准线的距离为,解得,所以抛物线方程为,即;
当时,抛物线开口向下,准线方程,点到准线的距离为,解得或(舍去),所以抛物线方程为,即.
所以抛物线的方程为或故选:D
【变式2】(2017·河南信阳·高二期末(理))抛物线的焦点坐标为
A. B. C. D.
【详解】将化为,则抛物线的焦点坐标为.故选B.
题型六:抛物线的对称性
例题6(2021·全国高二单元测试)以抛物线的顶点为圆心的圆交于,两点,交的准线于,两点,已知,,则抛物线的焦点到准线的距离为( )
A.2 B.4 C.6 D.8
解:不妨设抛物线的方程为,令点在第一象限,点在第二象限.
根据抛物线的对称性,得点的纵坐标为,代入抛物线的方程得,即点.
又点.因为点,都在以坐标原点为圆心的圆上,所以,解得或(舍去),
则抛物线的焦点到准线的距离为4.故选:B.
举一反三:
【变式1】(2021·中国农业大学附属中学)若正三角形的顶点都在抛物线上,其中一个顶点恰为坐标原点,则这个三角形的面积是( )
A. B. C. D.
【详解】设三角形其中一个顶点为,
因为三角形是正三角形,
所以,即,解得,
所以三角形的两个顶点为,
所以三角形的面积为,故选:A
【变式2】(2021·全国高二课时练习)是抛物线上的两点,为坐标原点.若,且的面积为,则( )
A. B. C. D.
【详解】如图,
∵,知两点关于轴对称,
设,
∴,解得,
∴,∴,
∴,∴.故选:C
题型七:抛物线的弦长问题
例题7.(2021·全国高二课时练习)过抛物线的焦点作直线交抛物线于,两点(,的横坐标不相等),弦的垂直平分线交轴于点,若,则( )
A.14 B.16 C.18 D.20
设,,弦的中点为,,
则,
所以,所以,
则,
所以弦的垂直平分线为.
令,则,所以.
又,
所以.故选:D.
举一反三:
【变式1】(2021·马鞍山市第二中学郑蒲港分校高二开学考试(文))过拋物线:焦点F的直线与抛物线相交于A,B两点,,O为坐标原点,且△的面积为,则抛物线C的标准方程为( )
A. B. C. D.
【详解】由题设,令为,联立抛物线方程并整理得,
∴若,则,,又易得,
∴,则,即,
∴,
又,而,
∴,即,又,则,故.故选:D
【变式2】(2021·河北运河·沧州市一中高二开学考试)已知直线与抛物线:相交于,两点,为抛物线的焦点.若,则等于( )
A.7 B.8 C.9 D.10
【详解】,又,
,
,
直线方程为,代入抛物线方程,得:
,
,
,故选:C.
题型八:抛物线的焦点弦性质问题
例题8(2021·全国高二课时练习)已知抛物线的顶点在原点,焦点在轴正半轴上,过其焦点作直线交抛物线于,两点,过点,分别作抛物线准线的垂线,垂足分别为点,,,且,则该抛物线的方程为( )
【详解】设,,,
抛物线的方程为,,
由可得,
所以
所以,,
所以,,,,
所以,, ,,
所以,
因为,所以,所以,
所以抛物线的方程为.故选:A.
举一反三:
【变式1】(2020·江苏高二课前预习)已知抛物线的顶点在坐标原点,准线方程为,过其焦点的直线与抛物线交于,两点,若直线的斜率为1,则弦的长为( )
A.4 B.6 C.7 D.8
解:依题意得,抛物线的方程是,直线的方程是.联立
消去,得,即.设,,则,所以.
故选:D.
【变式2】(2021·四川自贡·高二期末(文))已知抛物线的焦点为,准线为,过焦点的直线交抛物线于、两点,、两点分别为、两点在直线上的射影,而且,为线段的中点.则下列命题( )
① ②等腰直角三角形
③直线的斜率为
④的面积为4(为坐标原点),其中正确的命题个数为( )
A.1 B.2 C.3 D.4
【详解】根据题意可得焦点F(1,0),准线方程为x=-1,由题意可得直线BA的斜率不为0,
可设直线AB的方程为x=my+1设A(x1,y1),B(x2,y2),由题意可知,将直线AB与抛物线方程联立得y2-4my-4=0所以.
对于①:所以FC⊥FD,即∠CFD=90°,故①正确;
对于②:由①可得,不可能CM⊥DM,更不会∠C或∠D为直角,故B不正确;
对于③:因为,所以,即,
因为所以解得,所以,
所以直线的斜率为.故③正确;
对于④:由題意可得,
点O到直线AB的距离,
所以,故④错误.故选:B
题型九:直线与抛物线的位置关系
例题9(2021·贵州师大附中高二月考(理))已知抛物线:,过其焦点且斜率为2的直线与抛物线交于,两点,若线段中点的纵坐标为1,则抛物线的准线方程为( )
A. B. C. D.
【详解】抛物线的焦点坐标为,
所以直线AB为,将其代入抛物线方程可得,
设,则,因为线段中点的纵坐标为1,所以,所以准线方程为,故选:B
举一反三:
【变式1】(2021·全国高二课时练习)直线与抛物线有且只有一个公共点,则,满足的条件是( )
A. B.,
C., D.或
【详解】当时,直线与抛物线有且只有一个公共点,符合题意;
当时,由可得:,
若直线与抛物线有且只有一个公共点,
则,整理可得:,所以,
综上所述:或,故选:D.
【变式2】(2021·全国高二课时练习)已知点,在抛物线上,为坐标原点,若,且的垂心恰好是此抛物线的焦点,则直线的方程是( )
A. B. C. D.
【详解】如图所示,为的垂心,为焦点,
,垂直平分线段,直线垂直于轴.
设,,其中.
为垂心,,,
即,解得,
直线的方程为,即.
故选:C.
题型十:抛物线的定值、定点、定直线问题
例题10(2021·全国高二课时练习)已知抛物线的顶点在坐标原点,焦点在轴的正半轴上,直线与抛物线交于,两点,且.
(1)求抛物线的标准方程.
(2)在轴上是否存在一点,使为正三角形?若存在,求出点的坐标;若不存在,请说明理由.
【详解】(1)由题意,设所求抛物线的标准方程为.
由,消去,得.
设,,则,.
由,
得,解得或(舍去),
∴抛物线的标准方程为.
(2)设的中点为点,则.
假设在轴上存在满足条件的点,连接.
∵为正三角形,∴,即,
解得,∴,∴.
又,
∴在轴上不存在一点,使为正三角形.
举一反三:
【变式1】(2021·全国高二课时练习) 已知抛物线C:y2=4x,A,B,其中m>0,过B的直线l交抛物线C于M,N.
(1)当m=5,且直线l垂直于x轴时,求证:△AMN为直角三角形;
(2)若=+,当点P在直线l上时,求实数m,使得AM⊥AN.
解:(1)证明:由题意,l:x=5,代入y2=4x中,解得,
不妨取M(5,),N(5,-),则,
∴,∴AM⊥AN,即△AMN为直角三角形,得证.
(2)由题意,四边形OAPB为平行四边形,则kBP=kOA=2,
设直线l:y=2(x-m),,联立,得y2-2y-4m=0,
由题意,判别式Δ=4+16m>0,y1+y2=2,y1y2=-4m,
∵AM⊥AN,则,又,
∴,化简得(y1+2)(y2+2)+16=0,即y1y2+2(y1+y2)+20=0,
∴,解得m=6,故m=6时,有AM⊥AN.
【变式2】(2021·重庆市第六十六中学校高二月考)已知动圆过定点,且与直线相切,
(1)求动圆圆心的轨迹方程;
(2)过点作曲线的两条弦,设、所在直线的斜率分别为、,当、变化且满足时,证明直线恒过定点,并求出该定点的坐标.
解:(1)∵动圆过定点,且与直线相切,
∴曲线是以点为焦点,直线为准线的抛物线,其方程为:.
(2)∵直线与抛物线有两个不同的交点
∴直线的斜率必不为0.
∴设其方程为,并设点,点,与抛物线联立得:.
∴整理得:,其中,,且
∵
.
∴.
∴.
∴.
∴.
∴或.
当时,直线的方程可化为:,过定点;
当时,直线的方程可化为:,过定点,即点不合题意,舍去.
∴直线必过定点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
