华东师大版七上数学 3.1.3列代数式 课件(共16张PPT)
文档属性
| 名称 | 华东师大版七上数学 3.1.3列代数式 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 490.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 14:23:53 | ||
图片预览






文档简介
(共16张PPT)
3.列代数式
⑴代数式中出现的乘号,通常写作“.”或省
略不写,如6×b常写作6·b或6b
⑵数字与字母相乘时,数字写在字母
前面,如6b一般不写作b6.
写代数式要注意:
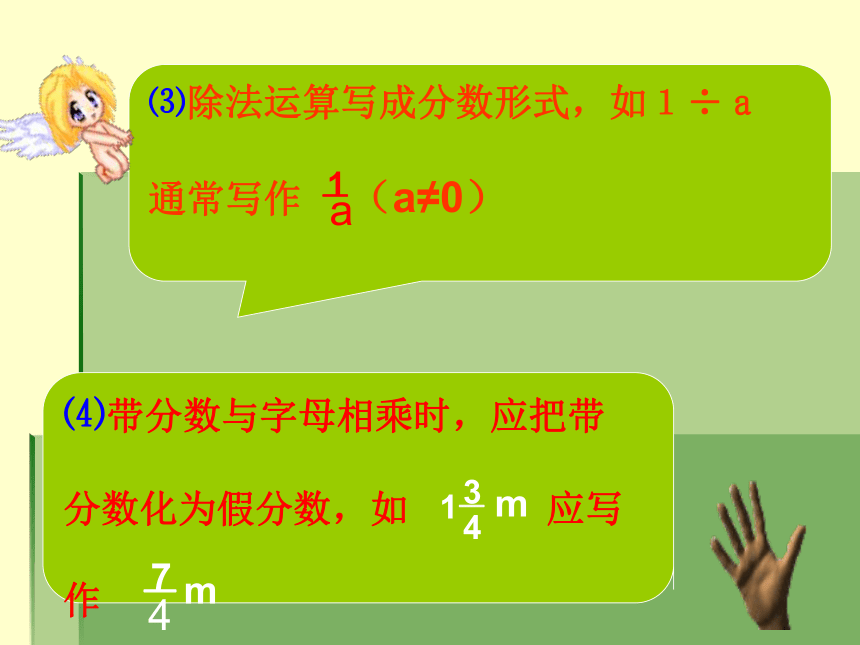
⑶除法运算写成分数形式,如1÷a
通常写作 (a≠0)
1
a
-
⑷带分数与字母相乘时,应把带
分数化为假分数,如 应写
作
1
4
3
-
m
7
4
-
m
(5)用代数式表示具有实际意义的量时,
如果所列的代数式是“和”或“差”的形式,
并且有单位,那么必须把所列代数式用
括号括起来,后面写上单位。
例1 设甲数为x,用代数式表示乙数:
(1)乙数比甲数大5;
(2)乙数比甲数的2倍小3;
(3)乙数比甲数大16%;
(4)乙数比甲数的倒数小7。
解:
(1)x+5
(2)2x-3
(3)(1+16%)x
(4) -7
例2设甲数为a,乙数为b,用代数式表示:
(1)甲乙两数的和的2倍;
(2)甲数的1/3与乙数的1/2的差;
(3)甲乙两数的平方和(或差);
(4) 甲乙两数的和(或差)的平方;
(5)甲乙两数的和与甲乙两数的差的积;
(6)甲乙两数的平方和减去它们乘积的
2倍;
(7) 甲乙两数的和的平方减去它们的差
的平方;
例3用代数式表示:
(1)被3整除得n的数;
(2)被5除商m余2的数。
(3)偶数、奇数
(4)三个连续奇数
(5)一个两位数,个位数字为x,十位数字比个位数字小1。
解(1)3n,
(2)5m+2
例4 设字母a表示一个数,用代数式表 示:
(1)这个数与5的和的3倍;
(3)这个数的5倍与7的和的一半;
例5.
1.设甲数为x,乙数为y,用代数式表示:
(1)甲乙两数之积与甲乙两数之和的差;
(2)甲乙的差除以甲乙两数的积的商.
2.用代数式表示:
(1)比a与b的差的一半大1的数;
(2)比a除以b的商的3倍大8的数;
(3)比a除b的商的3倍大8的数.
3.用代数式表示:
(1)与a-1的和是25的数;
(2)与2b+1的积是9的数;
列代数式的方法:
(1)认真审题:抓住关键性的词、字,
如“大”、“小”、“多”、“少”、“和”
“差”、“倍”、“商”、“倒数”、“平方差”、
“平方和”“余数”、“平方”、“立方”、
“增加”等等;
列代数式的方法:
(2)正确判断各种数量关系中的运算顺序:
通常是先读的先写,后读的运算后写,并且
正确对待遵循运算顺序(先乘方,后乘除,
最后加减)和运算括号(先括号内,后括
号外;先小括号,再中括号 ,最后大括号)
列代数式的方法:
(3)对于 复杂的题目,应“浓缩原题,
分段处理,最后组装”。如“a的2倍与b的
平方的和”与“b的立方与a的倒数之差”的积,
此题可浓缩为“两数和与两数差的积”,第一
段可列出:“2a+b2”,第二段可列出b3-1/a,
故所列出的代数式为
(4)要理解掌握基本的数量关系:
路程=时间 x 速度
工作量=工作时间x工作效率
总价=单价x数量
溶质=溶液x浓度
1、一个三角形的三条边分别长a、b、c,求这个三角形的周长.
2、张强比王华大3岁,当张强a岁时,王华的年龄是多少?
3、飞机的速度是汽车的40倍,自行车的速度是汽车的1/3,如果汽车的速度是v千米/时,,那么,飞机与自行车的速度个是多少?
4、a千克大米的售价是6元,1千克大米售多少元?
5、圆的半径是Rcm,它的面积是多少?
6、说出下列代数式的意义:
(1) 3x+6 (2)5(x-2)
(3) (4)
作业:1、用代数式表示:
(1)长为a米,宽为b米的长方形的周长;
(2)宽为b米,长是宽的2倍的长方形的周长;
(3)长为a米,宽是长的1/3的长方形的周长;
(4)宽为b米,长比宽多2米的长方形的周长.
2、指出下列每小题中,两个代数式的意义有什么不同:
(1)a-b+c与a-(b+c)
(2)2m-1与2(m-1)
(3)
(4)
3、(1)利用乘法可以把2+2+2表示成2x3.如果用a表示任意一个数,利用乘法可以把a+a+a表示成什么?
(2)利用分配律可以得到2x6+3x6=(2+3)x6.如果用a表示任意一个数,那么利用分配律可以得到2a+3a等于什么?
3.列代数式
⑴代数式中出现的乘号,通常写作“.”或省
略不写,如6×b常写作6·b或6b
⑵数字与字母相乘时,数字写在字母
前面,如6b一般不写作b6.
写代数式要注意:
⑶除法运算写成分数形式,如1÷a
通常写作 (a≠0)
1
a
-
⑷带分数与字母相乘时,应把带
分数化为假分数,如 应写
作
1
4
3
-
m
7
4
-
m
(5)用代数式表示具有实际意义的量时,
如果所列的代数式是“和”或“差”的形式,
并且有单位,那么必须把所列代数式用
括号括起来,后面写上单位。
例1 设甲数为x,用代数式表示乙数:
(1)乙数比甲数大5;
(2)乙数比甲数的2倍小3;
(3)乙数比甲数大16%;
(4)乙数比甲数的倒数小7。
解:
(1)x+5
(2)2x-3
(3)(1+16%)x
(4) -7
例2设甲数为a,乙数为b,用代数式表示:
(1)甲乙两数的和的2倍;
(2)甲数的1/3与乙数的1/2的差;
(3)甲乙两数的平方和(或差);
(4) 甲乙两数的和(或差)的平方;
(5)甲乙两数的和与甲乙两数的差的积;
(6)甲乙两数的平方和减去它们乘积的
2倍;
(7) 甲乙两数的和的平方减去它们的差
的平方;
例3用代数式表示:
(1)被3整除得n的数;
(2)被5除商m余2的数。
(3)偶数、奇数
(4)三个连续奇数
(5)一个两位数,个位数字为x,十位数字比个位数字小1。
解(1)3n,
(2)5m+2
例4 设字母a表示一个数,用代数式表 示:
(1)这个数与5的和的3倍;
(3)这个数的5倍与7的和的一半;
例5.
1.设甲数为x,乙数为y,用代数式表示:
(1)甲乙两数之积与甲乙两数之和的差;
(2)甲乙的差除以甲乙两数的积的商.
2.用代数式表示:
(1)比a与b的差的一半大1的数;
(2)比a除以b的商的3倍大8的数;
(3)比a除b的商的3倍大8的数.
3.用代数式表示:
(1)与a-1的和是25的数;
(2)与2b+1的积是9的数;
列代数式的方法:
(1)认真审题:抓住关键性的词、字,
如“大”、“小”、“多”、“少”、“和”
“差”、“倍”、“商”、“倒数”、“平方差”、
“平方和”“余数”、“平方”、“立方”、
“增加”等等;
列代数式的方法:
(2)正确判断各种数量关系中的运算顺序:
通常是先读的先写,后读的运算后写,并且
正确对待遵循运算顺序(先乘方,后乘除,
最后加减)和运算括号(先括号内,后括
号外;先小括号,再中括号 ,最后大括号)
列代数式的方法:
(3)对于 复杂的题目,应“浓缩原题,
分段处理,最后组装”。如“a的2倍与b的
平方的和”与“b的立方与a的倒数之差”的积,
此题可浓缩为“两数和与两数差的积”,第一
段可列出:“2a+b2”,第二段可列出b3-1/a,
故所列出的代数式为
(4)要理解掌握基本的数量关系:
路程=时间 x 速度
工作量=工作时间x工作效率
总价=单价x数量
溶质=溶液x浓度
1、一个三角形的三条边分别长a、b、c,求这个三角形的周长.
2、张强比王华大3岁,当张强a岁时,王华的年龄是多少?
3、飞机的速度是汽车的40倍,自行车的速度是汽车的1/3,如果汽车的速度是v千米/时,,那么,飞机与自行车的速度个是多少?
4、a千克大米的售价是6元,1千克大米售多少元?
5、圆的半径是Rcm,它的面积是多少?
6、说出下列代数式的意义:
(1) 3x+6 (2)5(x-2)
(3) (4)
作业:1、用代数式表示:
(1)长为a米,宽为b米的长方形的周长;
(2)宽为b米,长是宽的2倍的长方形的周长;
(3)长为a米,宽是长的1/3的长方形的周长;
(4)宽为b米,长比宽多2米的长方形的周长.
2、指出下列每小题中,两个代数式的意义有什么不同:
(1)a-b+c与a-(b+c)
(2)2m-1与2(m-1)
(3)
(4)
3、(1)利用乘法可以把2+2+2表示成2x3.如果用a表示任意一个数,利用乘法可以把a+a+a表示成什么?
(2)利用分配律可以得到2x6+3x6=(2+3)x6.如果用a表示任意一个数,那么利用分配律可以得到2a+3a等于什么?
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
