19.1平行四边形性质
图片预览





文档简介
(共23张PPT)
蒙公一中:秦庆奖
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形,
记作: ABCD 读作:平行四边形ABCD
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为 对边
相对的角称为 对角
有一条公共边的角称为 邻角
平行四边形相 关 概 念
A
D
C
B
线段AC就是 ABCD的一条对角线
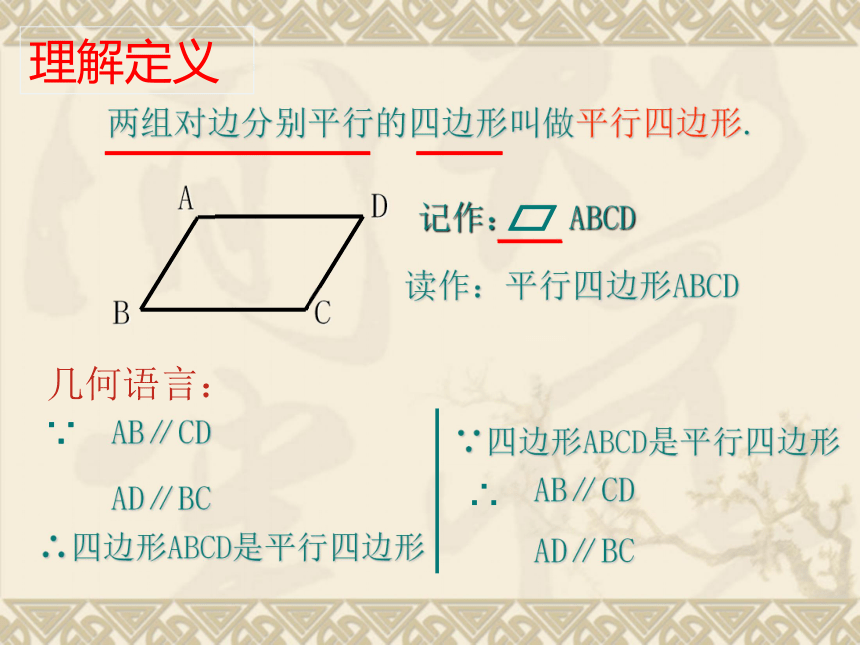
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
理解定义
几何语言:
A
B
C
D
根据定义可知平行四边形的对边互相平行。除此之外还有什么性质呢?这就是本节课要探讨的课题……
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
平行四边形的边、角有怎样的数量关系?
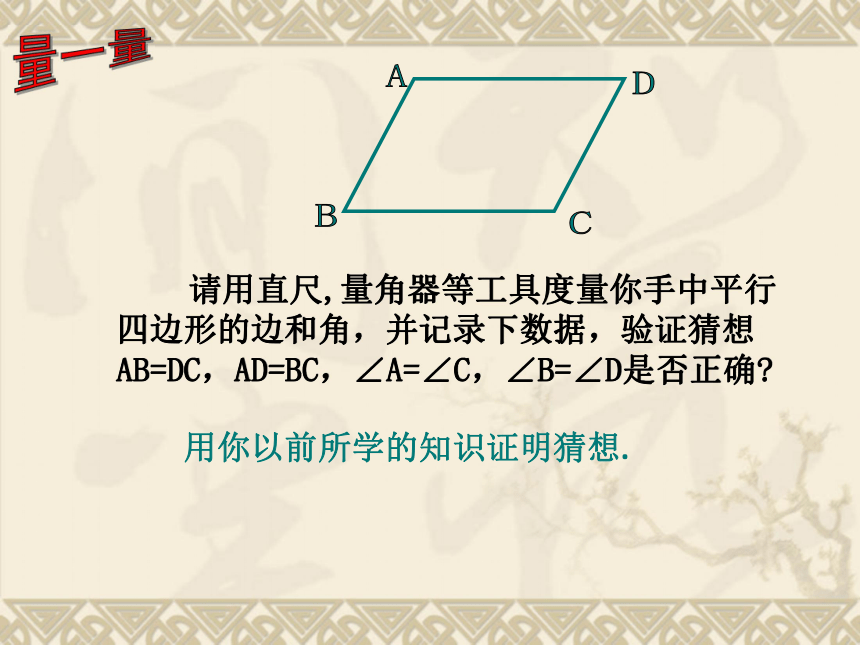
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确
用你以前所学的知识证明猜想.
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
几何语言:
定理1:平行四边形的两组对边分别相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
在 ABCD中,
AB=CD,AD=BC.(平行四边形的对边相等)
∠A=∠C, ∠B=∠D(平行四边形的对角相等)
∠A+∠B = 180° ∠A+∠D =180° (平行四边的邻角互补)
∠A=∠C, ∠B=∠D (平行四边形的对角相等)
∠A+∠B=180° ∠A+∠D =180° (平行四边的邻角互补)
定理2:平行四边形的两组对角分别相等推论: 平行四边的邻角互补
1.如图:在 ABCD中,根据已知你能得到哪
些结论?为什么
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
1.已知: ABCD中,∠A=100°,你能求出其他各角的度数吗?说说你的理由.
∠B=80°
∠C=100°
∠ D=80°
A
D
C
B
2.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
D
C
B
A
58°
28
32
58°
28
32
122°
28
32
如图: 小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少
解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m
A
D
B
C
8cm
A
B
D
C
E
9cm
5cm
4.如图所示,若BE平分∠ABC,则ED= .
4cm
2
3
5cm
5cm
4cm
1
3cm
A
B
D
C
5cm
4cm
3.求如图所示的四边形ABCD的面积.
3cm
1.如图, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A 6cm B 12cm C 4cm D 8cm
A
B
D
C
A
D
B
C
2.如图,在 ABCD中,∠A:∠B=7:2,求∠C的度数.
已知如图:E、F是平行四边形ABCD的对角线AC上的两点,AE=CF
求证(1)△ADF≌ △CBE
(2)EB∥DF
1
2
3
4
课堂回顾:
1:定义:两组对边分别平行的四边形叫做平行四边形.
2:性质:平行四边形的对边平行。
平行四边形的对边相等。
平行四边形的对角相等。
平行四边形的邻角互补。
3:性质的运用( 解决平行四边形的有关问题经常连结对角线转化为三角形。)
作业:
P90 1
P91 6
蒙公一中:秦庆奖
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形,
记作: ABCD 读作:平行四边形ABCD
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为 对边
相对的角称为 对角
有一条公共边的角称为 邻角
平行四边形相 关 概 念
A
D
C
B
线段AC就是 ABCD的一条对角线
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
理解定义
几何语言:
A
B
C
D
根据定义可知平行四边形的对边互相平行。除此之外还有什么性质呢?这就是本节课要探讨的课题……
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
平行四边形的边、角有怎样的数量关系?
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确
用你以前所学的知识证明猜想.
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
几何语言:
定理1:平行四边形的两组对边分别相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
在 ABCD中,
AB=CD,AD=BC.(平行四边形的对边相等)
∠A=∠C, ∠B=∠D(平行四边形的对角相等)
∠A+∠B = 180° ∠A+∠D =180° (平行四边的邻角互补)
∠A=∠C, ∠B=∠D (平行四边形的对角相等)
∠A+∠B=180° ∠A+∠D =180° (平行四边的邻角互补)
定理2:平行四边形的两组对角分别相等推论: 平行四边的邻角互补
1.如图:在 ABCD中,根据已知你能得到哪
些结论?为什么
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
1.已知: ABCD中,∠A=100°,你能求出其他各角的度数吗?说说你的理由.
∠B=80°
∠C=100°
∠ D=80°
A
D
C
B
2.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
D
C
B
A
58°
28
32
58°
28
32
122°
28
32
如图: 小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少
解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m
A
D
B
C
8cm
A
B
D
C
E
9cm
5cm
4.如图所示,若BE平分∠ABC,则ED= .
4cm
2
3
5cm
5cm
4cm
1
3cm
A
B
D
C
5cm
4cm
3.求如图所示的四边形ABCD的面积.
3cm
1.如图, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A 6cm B 12cm C 4cm D 8cm
A
B
D
C
A
D
B
C
2.如图,在 ABCD中,∠A:∠B=7:2,求∠C的度数.
已知如图:E、F是平行四边形ABCD的对角线AC上的两点,AE=CF
求证(1)△ADF≌ △CBE
(2)EB∥DF
1
2
3
4
课堂回顾:
1:定义:两组对边分别平行的四边形叫做平行四边形.
2:性质:平行四边形的对边平行。
平行四边形的对边相等。
平行四边形的对角相等。
平行四边形的邻角互补。
3:性质的运用( 解决平行四边形的有关问题经常连结对角线转化为三角形。)
作业:
P90 1
P91 6
